Использование MATLAB для оценки возможности комплексирования информационных сигналов на основе нечеткой логики и фильтрации Калмана

Автор - В. М. Понятский

При выполнении комплексирования сигналов от информационных систем одна из основных проблем заключается в определении границ, в которых следует использовать тот или иной набор сигналов и самих режимов работы. Рассматривается подход, основанный на оценке значений координат центра тяжести результирующей функции принадлежности нечеткой системы вывода. В соответствии с полученной оценкой координаты центра тяжести определяются режимы работы и веса информационных сигналов.

1. Постановка задачи

При использовании нескольких информационных систем (ИС) изменение условий работы или появление помех может приводить к тому, что меняется характер информационных сигналов и возникают ситуации, когда необходим выбор режима работы: использование одной из систем или их комплексирование.

В статье рассматривается метод комплексирования ИС на основе нечеткой логики и фильтрации Калмана. Использование нечеткой логики обеспечивает решение задачи определения границ режимов функционирования ИС и весов сигналов в соответствии с оценками значений координат центра тяжести результирующей функции принадлежности.

 

2. Алгоритм комплексирования информационных сигналов, основанный на фильтрации Калмана

Дискретный алгоритм оценивания состояния объекта управления в рамках методов фильтрации Калмана имеет вид [1 - 2]:

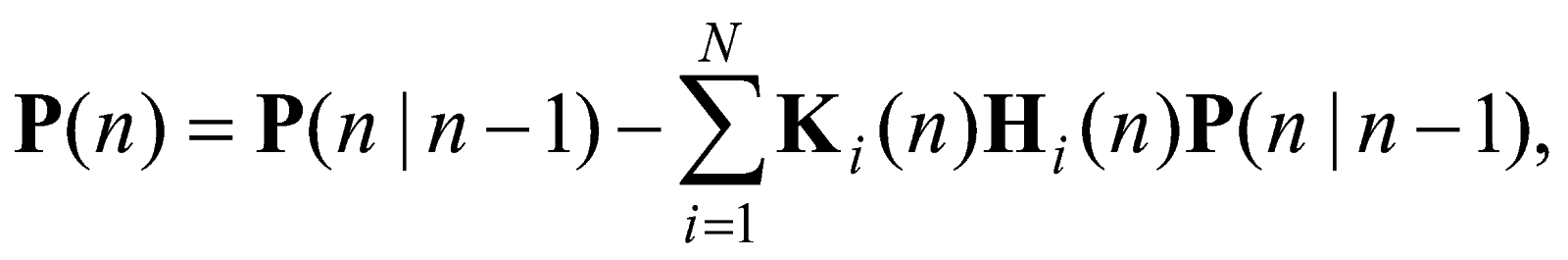
где – вектор наблюдений; – вектор оценок наблюдений; – оценка вектора состояния наблюдаемого объекта или процесса; – оценка скорректированного вектора состояния наблюдаемого объекта или процесса; – оценка вектора прогнозирования состояния наблюдаемого объекта или процесса; – матрица упреждения; – матрица наблюдения; – матрица коэффициентов; – дисперсионная матрица предсказания вектора состояния наблюдаемого объекта или процесса; – дисперсионная матрица оценки вектора состояния наблюдаемого объекта или процесса; – матрица интенсивности шумов; – матрица интенсивности полезного сигнала; – вектор управления; – матрица коэффициентов управления; – вектор весовых коэффициентов; – процедура коррекции оценок фильтра Калмана, – матрица, учитывающая тип и качество измерителя или отсутствия измерений ; – количество измерителей.

Непрерывный алгоритм фильтрации Калмана имеет вид [1-2]:

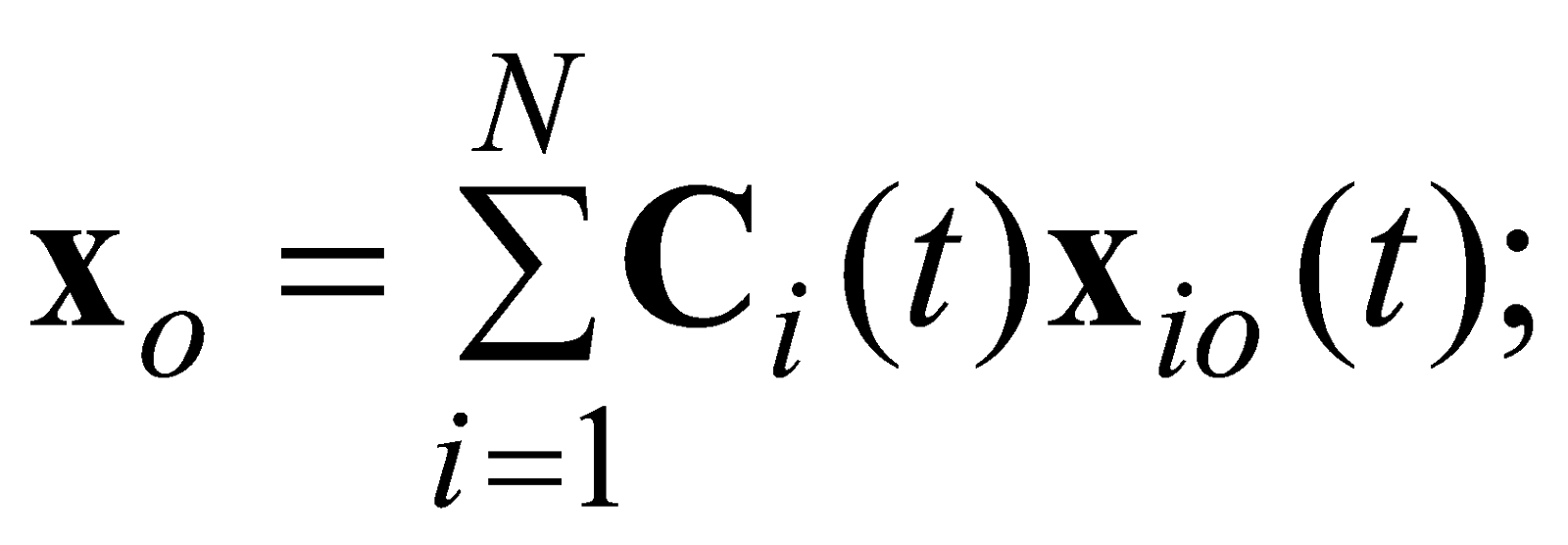
где – вектор измерений i-го датчика; – вектор оценок наблюдений; – оценка скорректированного вектора состояния наблюдаемого процесса; – оценка вектора состояния наблюдаемого процесса; – матрица упреждения; – корреляционная матрица ошибок фильтрации; – матрица наблюдения; – вектор коэффициентов усиления; – матрица интенсивности шумов; – матрица интенсивности полезного сигнала; – вектор управления; – матрица коэффициентов управления; – матрица весовых коэффициентов; – процедура коррекции оценки фильтра Калмана, – матрица, учитывающая тип и качества измерений или отсутствия измерений , - количество измерителей.

Рассматривается возможность регулирования полосы пропускания фильтра Калмана в соответствии с качеством функционирования каналов измерений.

 

3. Алгоритм оценки весов информационных сигналов, основанный на нечеткой логике

В работе [3] рассмотрен метод комплексирования информационных систем, основанный на нечеткой логике. Использование нечеткой логики определено двумя факторами:
1) отсутствием точного определения/формализации границ, в которых целесообразно использовать тот или иной набор сигналов;
2) необходимостью определения весов информационных сигналов при комплексировании.

Метод обеспечивает задание количественных границ для режимов работы и весов сигналов и основан на оценке значения координаты центра тяжести (ЦТ) результирующей функции принадлежности нечеткой системы вывода (НСВ) от входного параметра: предлагается границы режимов определять как области пересечения входных и выходных функций принадлежности НСВ, а весовые коэффициенты сигналов – как координаты ЦТ.

Для случая, когда имеется две информационные системы и один критерий качества функционирования, за который принято СКО сигнала, разработан алгоритм оценки весов информационных сигналов, основанный на нечеткой логике [3]. Для реализации полученного алгоритма в системе реального времени с ограниченными вычислительными ресурсами можно использование заранее рассчитанной траектории ЦТ в виде ломаной, полученной в соответствии с рассматриваемым методом:

где:

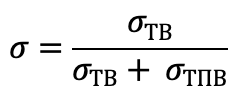– нормированная переменная;  и  – СКО сигнала ТВ- и ТПВ-каналов; РТВ и РТПВ – границы режимов работы.

Тогда значения весовых коэффициентов будут определяться уравнениями:

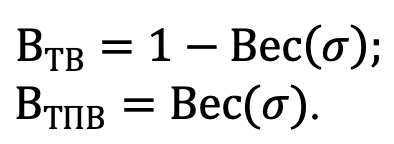
При этом следует отметить, что по полезному сигналу коэффициент передачи будет равен единице, а полоса пропускания будет постоянной, а по шумам для ТВ- и ТПВ-каналов коэффициенты передачи будут весовыми соответственно: В_ТВ/(В_ТВ+В_ТПВ) и В_ТПВ/(В_ТВ+В_ТПВ) и полосы пропускания будут меняться в соответствии уровнем СКО В_ТВ и В_ТПВ.

 

4. Результаты

Анализ описанного подхода проводится в среде MATLAB на примере оценки воздействия на систему, содержащую два измерителя. Оценка вектора состояния производится с помощью фильтрующих звеньев второго порядка. Для двухканального фильтра соответствующие матрицы выглядят следующим образом (рис. 1):

, , , , .

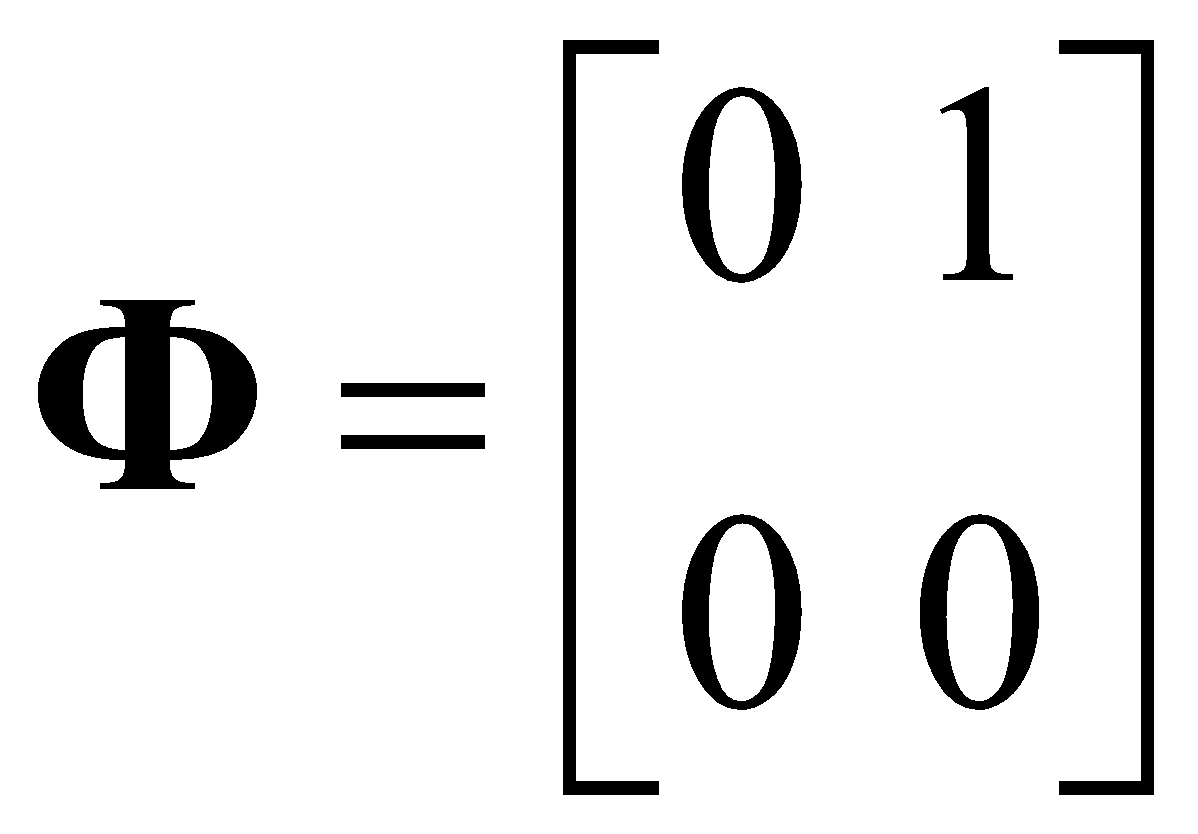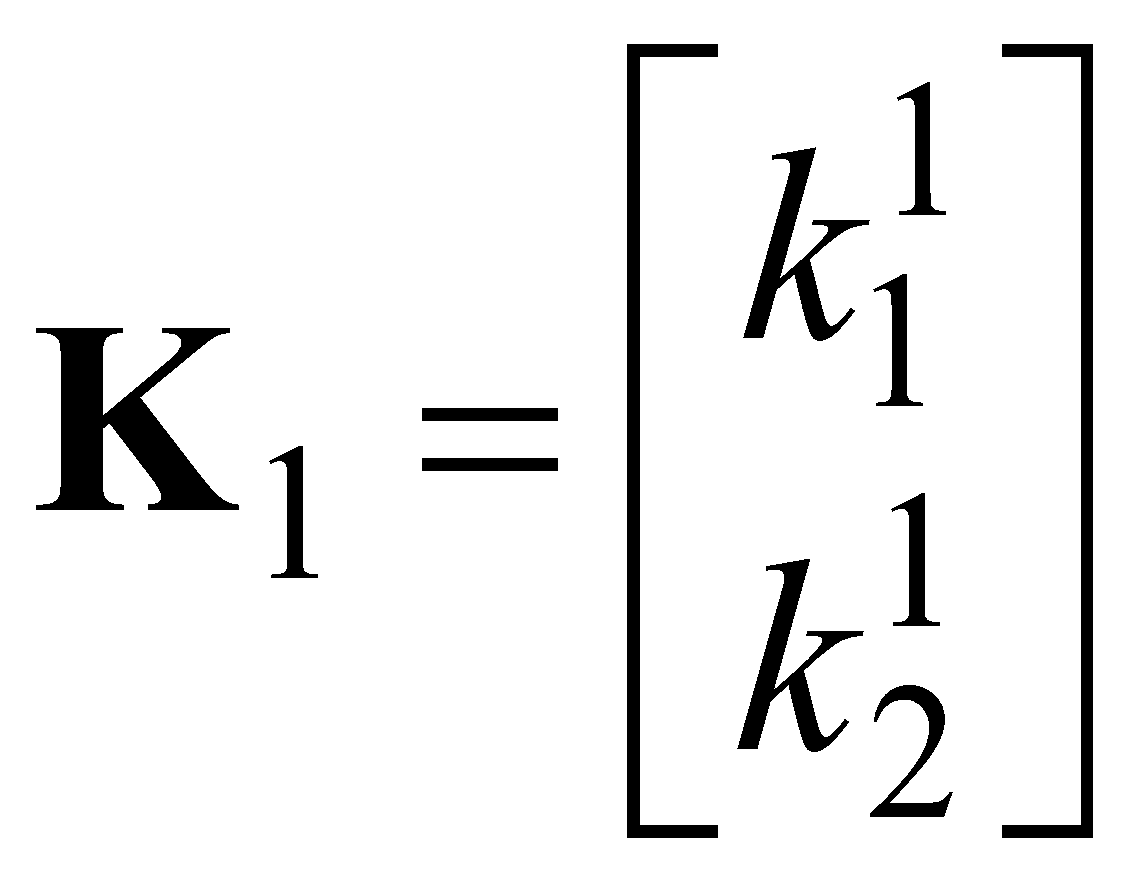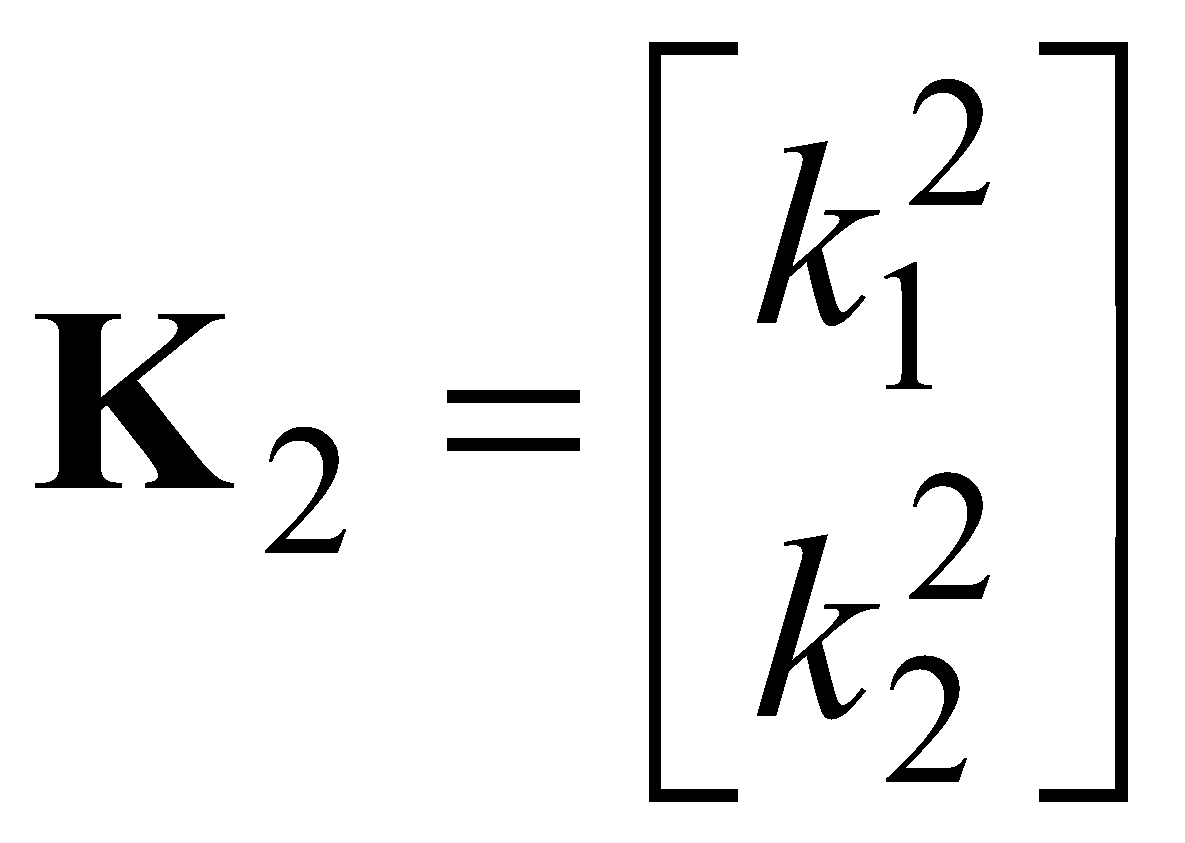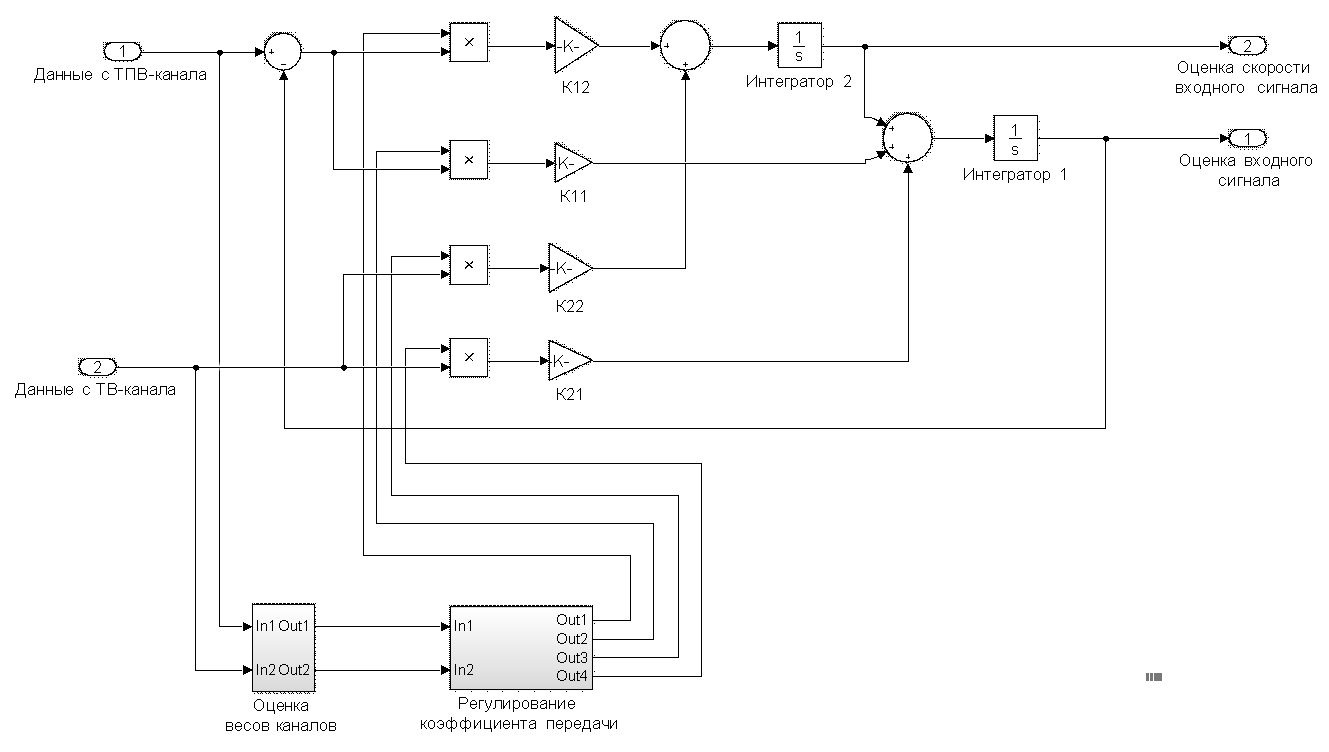
Рис. 1. Схема двухканального фильтра c с регулированием полосы пропускания

Для оценки алгоритма комплексирования на реальных сигналах были использованы телеметрические данные, полученные в ходе испытаний, представляющие собой информацию от ТВ- и ТПВ-каналов комплекса. Телеметрические данные (см. рис. 2 - 3) имеют статистики, приведенные в таблице.

Таблица – Статистики исходных сигналов

Сигнал	Мат. ожидание	Дисперсия	СКО
ТВ-канал	-0,0116	0,0003007	0,0173394
ТПВ-канал	0,0002	0,0001840	0,0135637

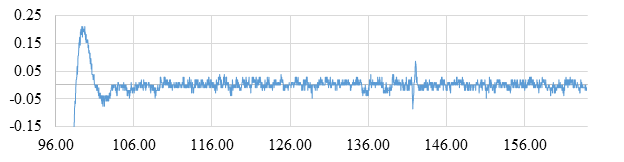
Рис. 2. Телеметрические данные от ТПВ-канала

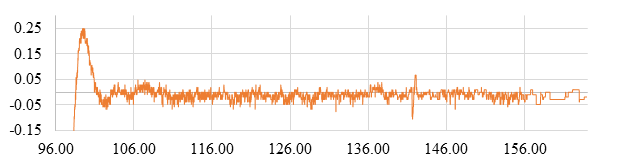
Рис. 3. Телеметрические данные от ТВ-канала

На рисунке 4 приведены оценки изменения полос пропускания в фильтре Калмана, полученные в соответствии с весами на выходе алгоритма комплексирования. Анализ расчета СКО для ТВ- и ТПВ-каналов показывает, что уровень помех выше в ТВ-канале (см. табл.) и следовательно, для лучшего подавления шумов полоса ТВ-канала более узкая, чем полоса ТПВ-канала (см. рис. 4).

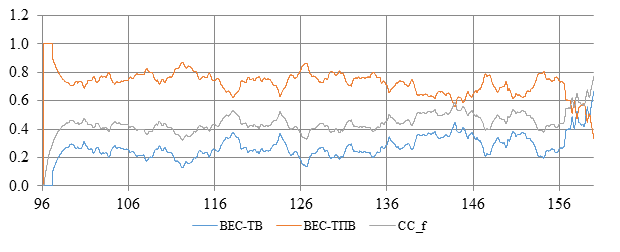
Риc. 4. Изменение полос пропускания фильтра Калмана по ТВ- и ТПВ-каналам: 

На рисунке 5 приведены результаты комплексирования сигналов на выходе фильтра Калмана для случая с регулированием полос пропускания по ТВ- и ТПВ-каналам.

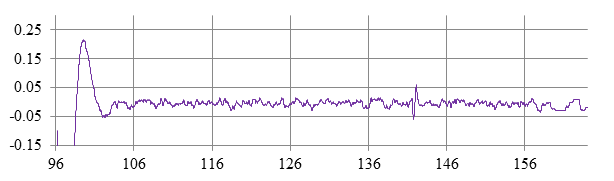
Рис. 5. Сигнал на выходе фильтра Калмана с регулированием полосы пропускания

Сравнение уровня шумов сигналов показывает, что комплексирование с помощью фильтра Калмана обеспечивает значительное уменьшение СКО шумов порядка 5-6 раз по сравнению с СКО самого точного канала (см. рис. 7).

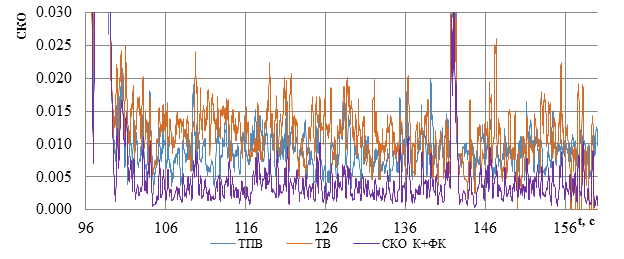
Рис. 6. СКО сигналов: ТВ-канал – ТВ; ТПВ-канал – ТПВ; сигнал на выходе фильтра Калмана с регулированием полос пропускания – СКО К+ФК

Таким образом, проведенное моделирование показало, что комплексирование двух каналов с разными уровнями среднеквадратического отклонения позволяет получить СКО суммарного сигнала гораздо меньшее, чем СКО самого точного канала.

 

Список литературы

1. Понятский В.М. Повышение качества обработки информации, поступающей с нескольких видеосенсоров, в задачах управления // Современные информационные технологии и ИТ-образование. 2016. Т. 12. № 4. С. 165–172.

2. Понятский В.М., Зенов Б.В. Применение фильтра Калмана для задач управления подвижными объектами // Современные информационные технологии и ИТ-образование. 2018. Т. 14. № 3. С. 625-630.

3. Понятский В.М., Горин А.В. Комплексирование сигналов от неравноточных информационных систем с помощью нечеткой логики // International Journal of Open Information Technologies. 2019. Т. 7, № 3. С. 25-31.