Использование MATLAB для оценки возможности выбора режима работы системы при комплексировании информационных сигналов на основе нечеткой логики

Авторы -  В. М. Понятский, А. В. Горин.

При выполнении комплексирования сигналов от информационных систем одна из основных проблем заключается в определении границ, в которых следует использовать тот или иной набор сигналов, и самих режимов работы. Рассматривается подход, основанный на оценке значений координат центра тяжести результирующей функции принадлежности нечеткой системы вывода. В соответствии с полученной оценкой координаты центра тяжести определяются режимы работы и веса информационных сигналов.

1. Постановка задачи

При использовании нескольких информационных систем (ИС) изменение условий работы или появление помех может приводить к тому, что меняется характер информационных сигналов и возникают ситуации, когда необходим выбор режима работы: использование одной из систем или их комплексирование.

В статье предлагается метод комплексирования ИС на основе нечеткой логики. Использование нечеткой логики определено двумя факторами: 1) отсутствием точного определения/формализации границ, в которых целесообразно использовать тот или иной набор сигналов (режим) и 2) необходимостью определения весов информационных сигналов при комплексировании.

Метод задания количественных границ для режимов работы и весов сигналов основан на оценке значения координаты центра тяжести (ЦТ) результирующей функции принадлежности нечеткой системы вывода (НСВ) от входного параметра: предлагается границы режимов определять как области пересечения входных и выходных функций принадлежности НСВ, а весовые коэффициенты сигналов – как координаты ЦТ.

 

2. Метод комплексирования информационных систем, основанный на нечеткой логике

Рассмотрим случай, когда имеется K ИС и N критериев их качества функционирования. Под критериями качества могут пониматься, например, величина математического ожидания, среднеквадратического отклонения (СКО) выходных сигналов систем и т. п.

Метод комплексирования информационных систем, основанный на нечеткой логике включает следующие шаги [2].

1) Определяется количество входов и выходов НСВ, в зависимости от количества комплексируемых ИС и используемых критериев качества (общий вид такой НСВ представлен на рис. 1).

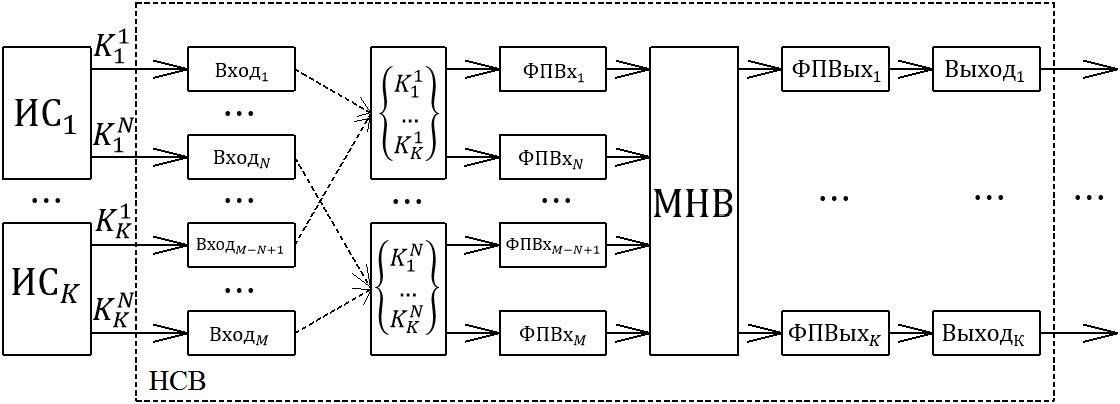
Рис. 1. Общий вид НСВ с М входами и К выходами: МНВ – модель нечеткого вывода, ФПВх – функция принадлежности входа, ФПВвых, – функция принадлежности выхода

2) Определяется вид функций принадлежности  входов и K выходов НСВ.

3) Вводятся границы функций принадлежности входов () и выходов ().

4) Для функций принадлежности входов задается нормированное значение параметра качества ИС, в общем случае определяемое как:

 , ,

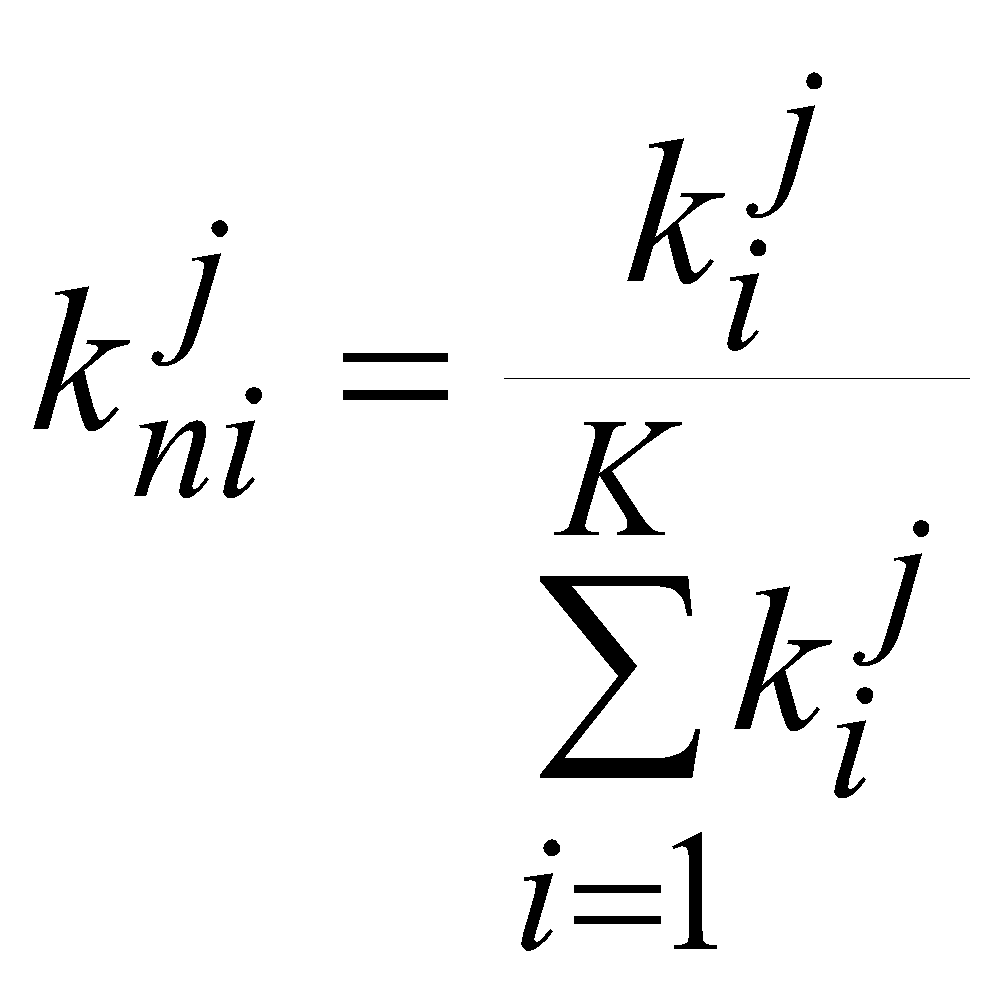где  – нормированный показатель качества,  – j показатель качества i-ой ИС, К – количество комплексируемых ИС, N – количество показателей качества.

5) Для определения координаты ЦТ используется один из алгоритмов нечеткого вывода, включающий формирование базы правил НСВ, фаззификацию входных переменных; агрегирование подусловий в нечетких правилах продукций; агрегирование подзаключений в нечетких правилах продукций; аккумуляцию заключений нечетких правил продукций и дефаззификация выходных переменных (расчет координаты ЦТ).

 

3. Результаты

Рассмотрим случай, когда имеется две ИС и один критерий качества функционирования, за который принято СКО сигналов ИС.

Формирование траектории ЦТ включает следующие шаги:

1) Поскольку имеется две ИС и один критерий, используется НСВ с одним входом и одним выходом (рис. 2).

2) В качестве функций принадлежности входа и выхода НСВ используются левосторонние и правосторонние треугольные множества.

3) Границы функций принадлежности входов () и выходов () выбраны равными 0,7 и 0,2 соответственно.

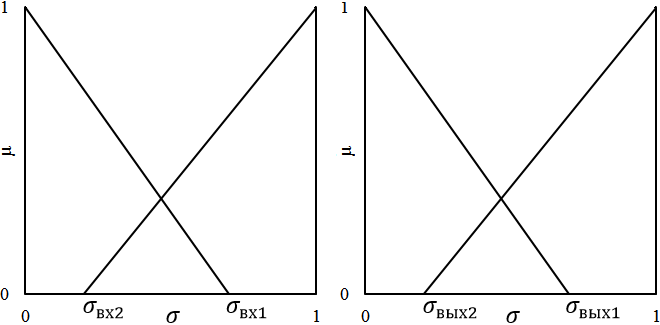
Рис. 2. Функции принадлежности входа и выхода (где  и  – границы функций входа,  и  – границы функций выхода

4) Нормированное значение параметра качества ИС:

 ,

где  – нормированное значение; – СКО выходного сигнала первой ИС;  – СКО выходного сигнала второй ИС.

Значение функции принадлежности входов и выходов (рис. 2) для нечетких множеств определяется формулами [1]:

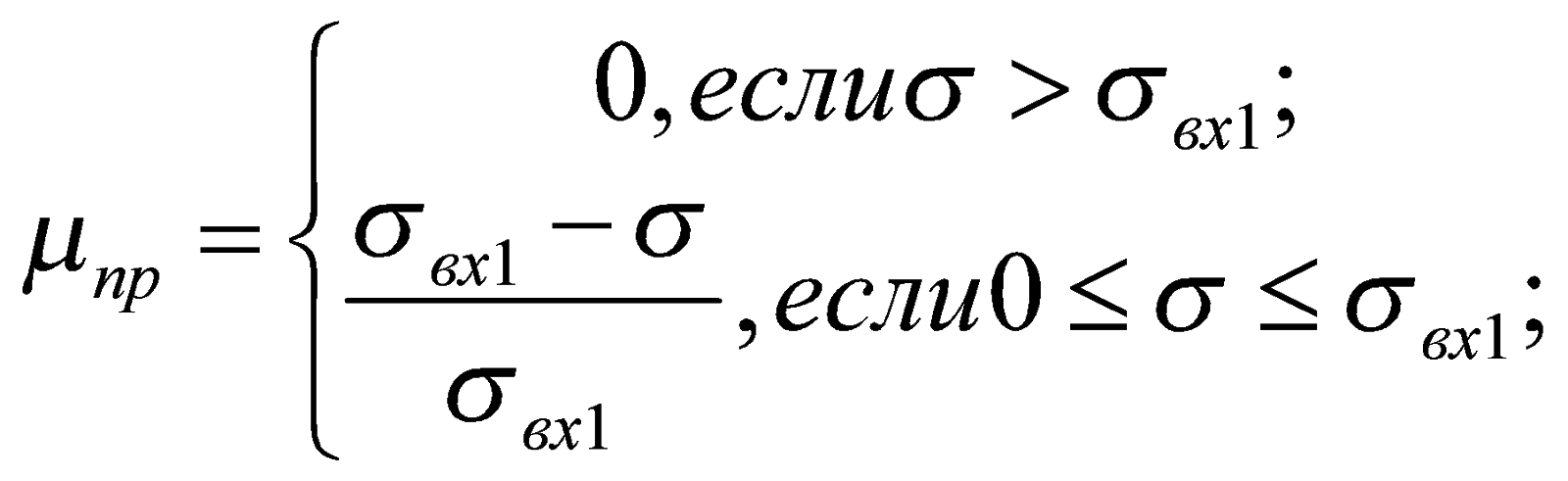
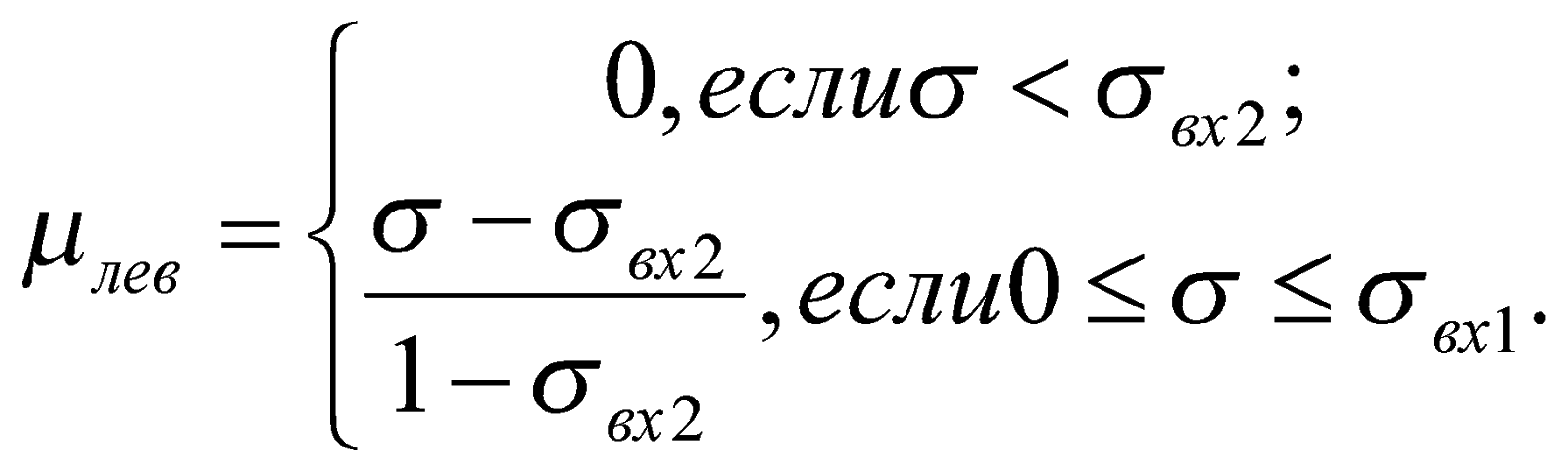
• интервал от 0 до 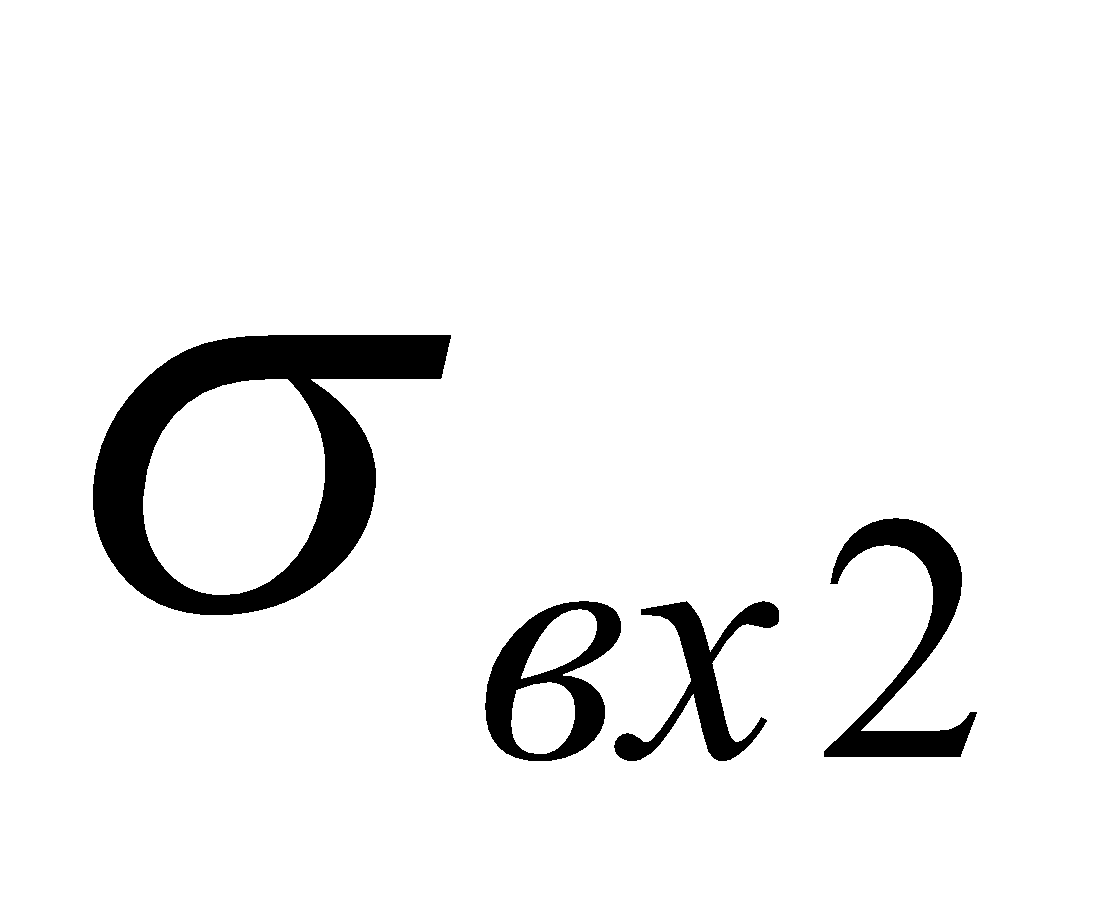 соответствует режиму, в котором используется только вторая BC; 
• интервал от 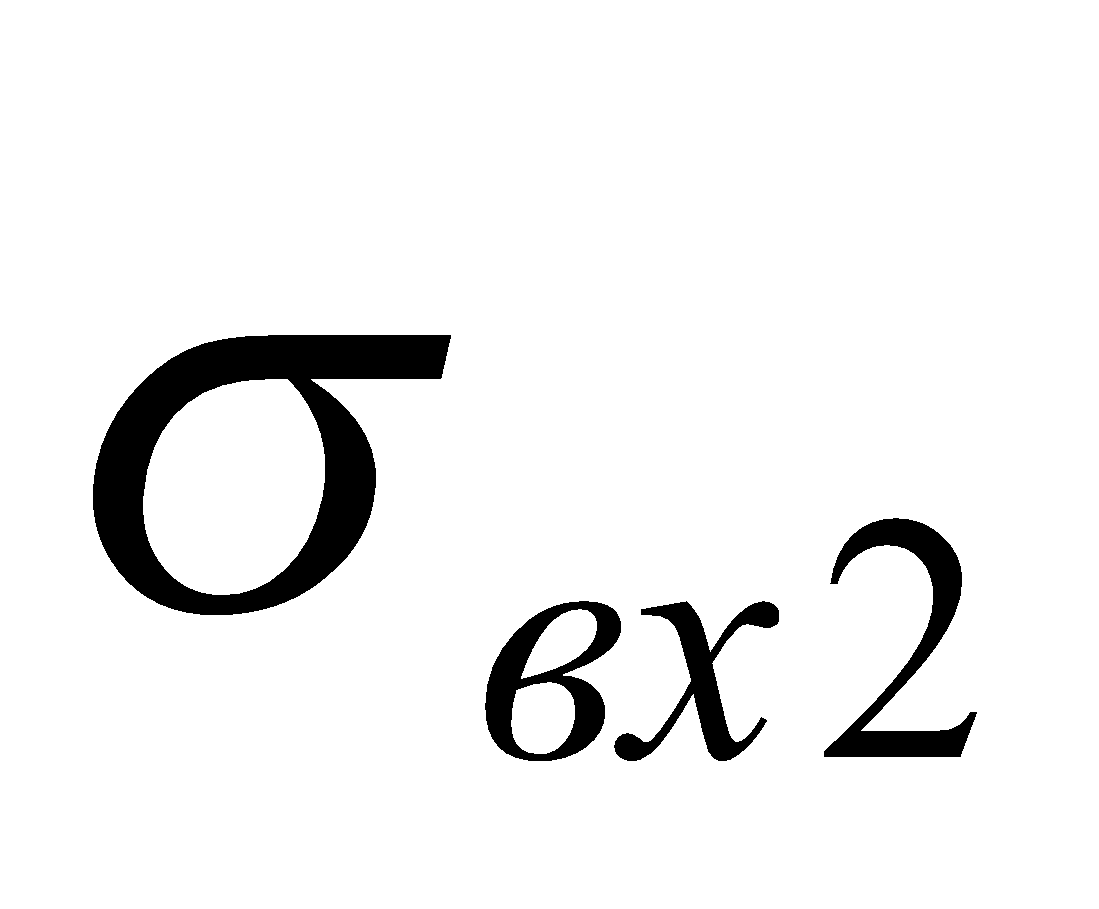 до 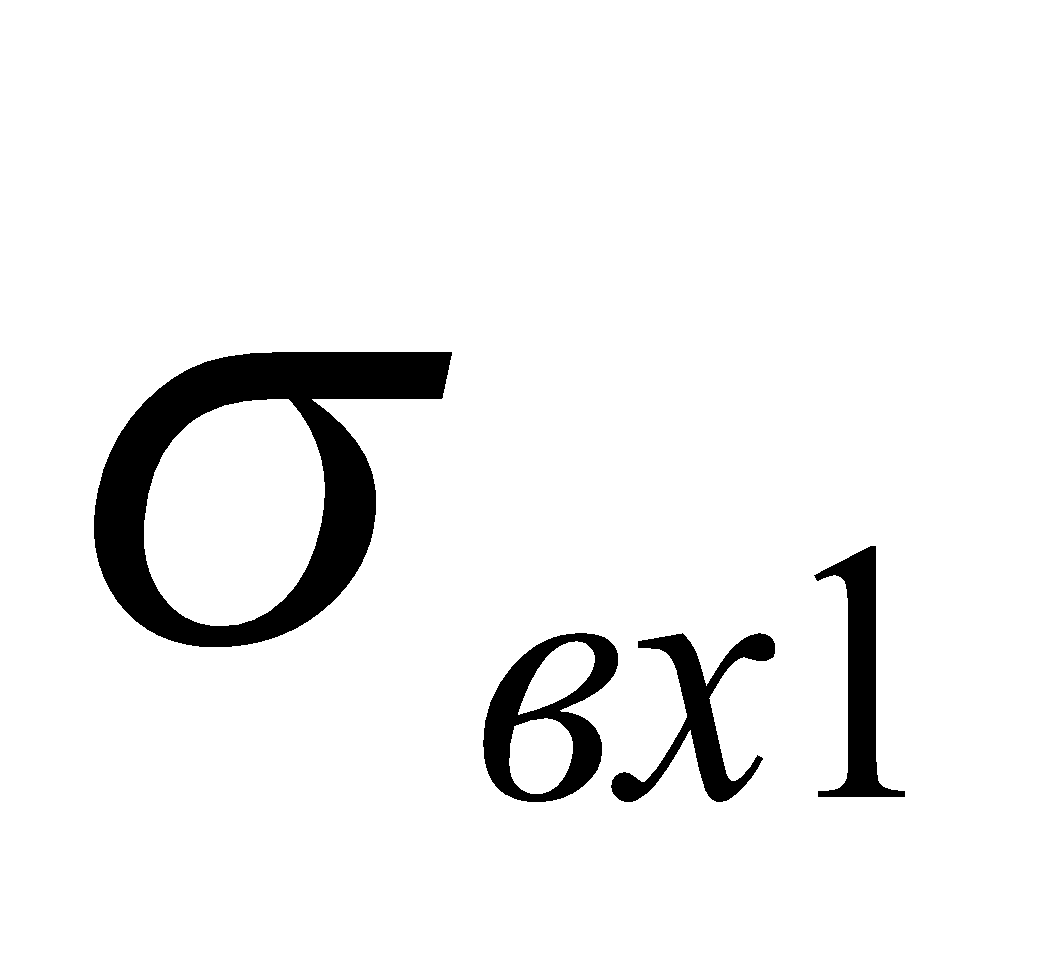 – режиму комплексирования; 
• интервал от 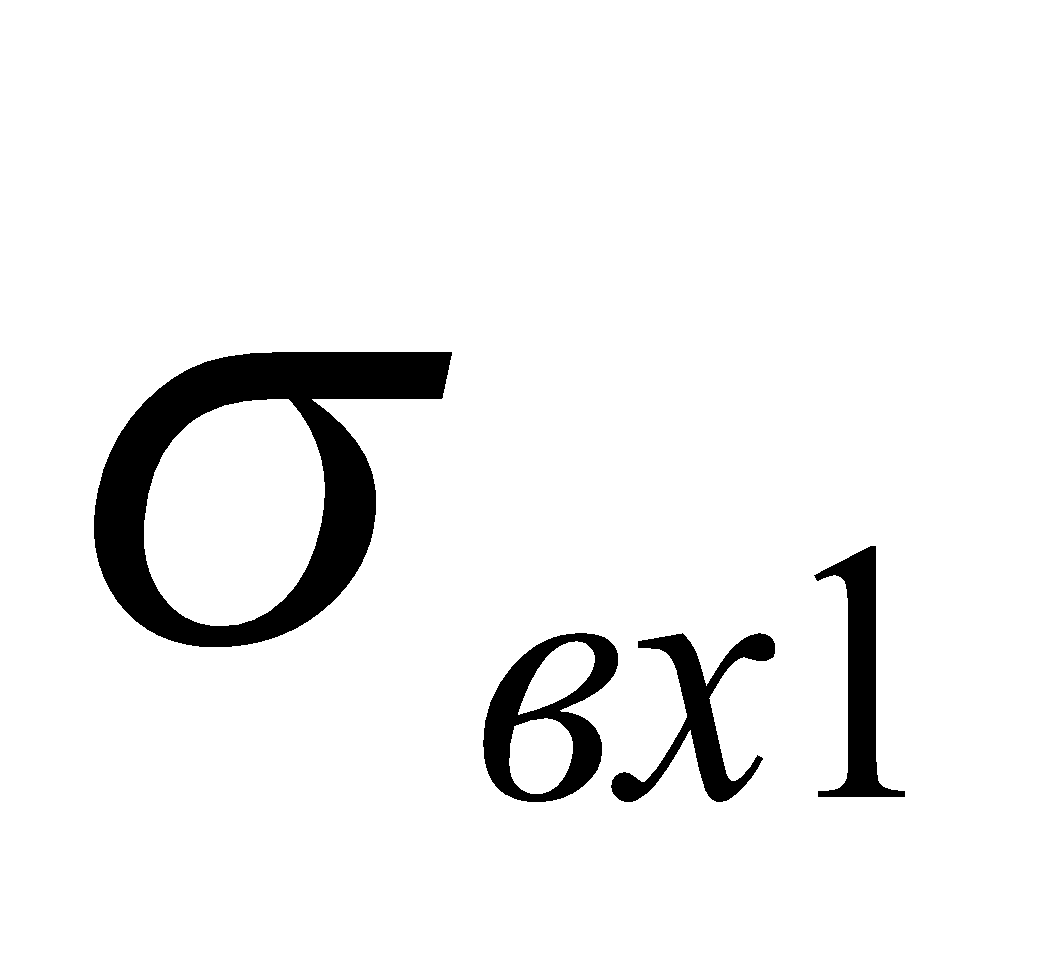 до 1,0 – режиму использования только первой BC).

5) Координаты ЦТ вычисляются с помощью алгоритм Мамдани, включающего следующие шаги [4]:

• формирование базы правил НСВ. База правил НСВ основана на возможном множестве значений нормированного значения и состоит из следующих основных правил нечетких продукций:
• если , то  и выбирается вторая система;
• если , то 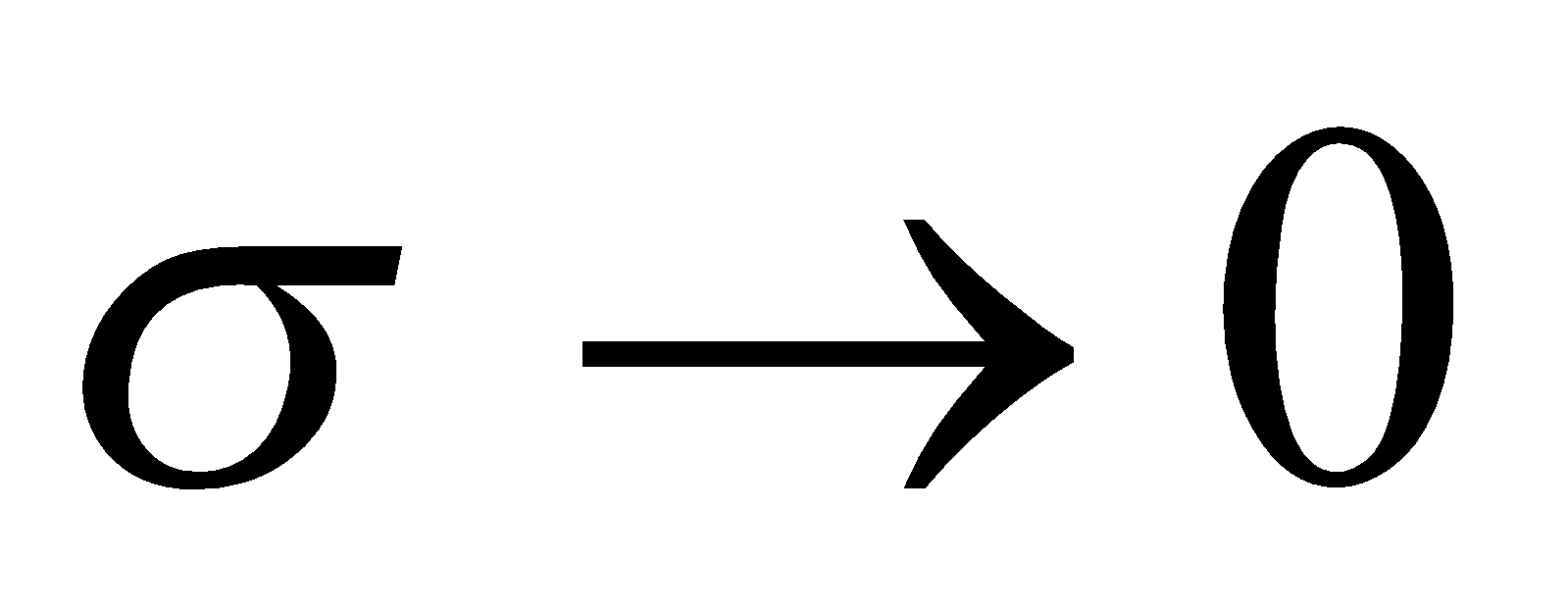 и выбирается первая система;
• если 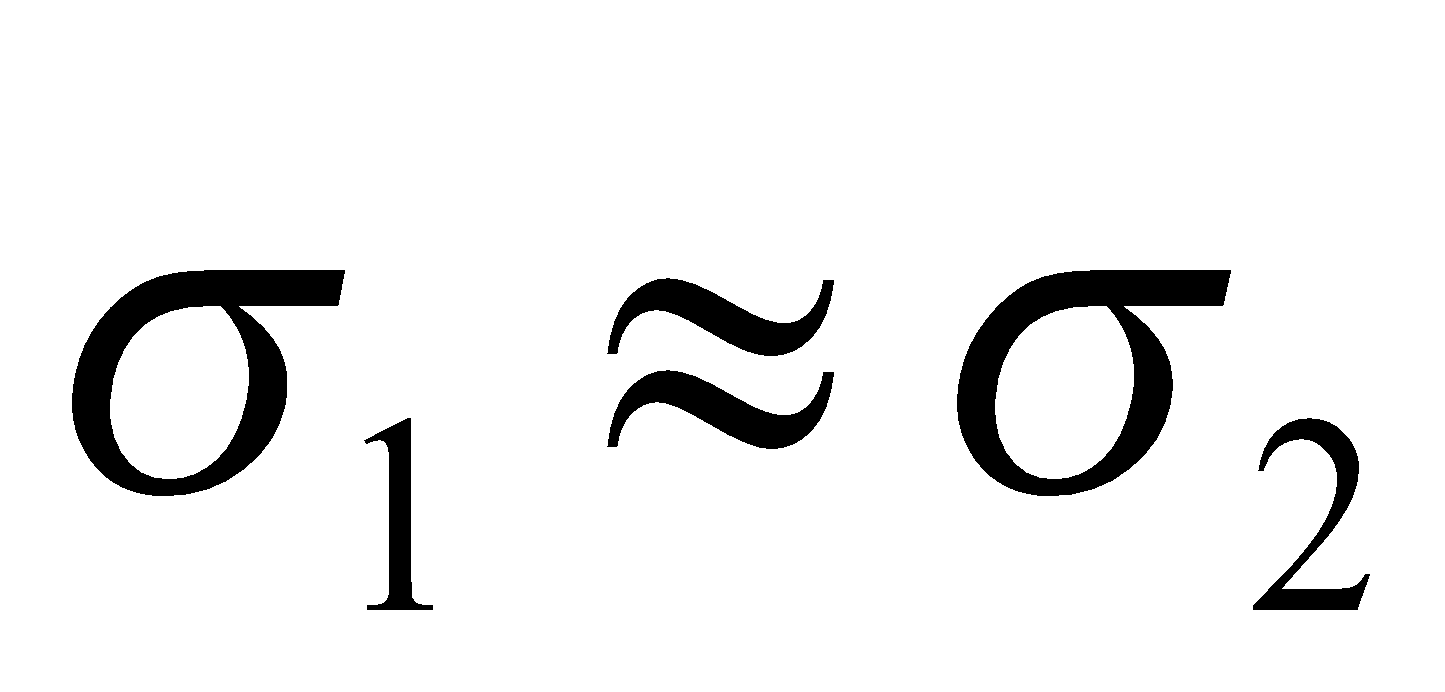, то 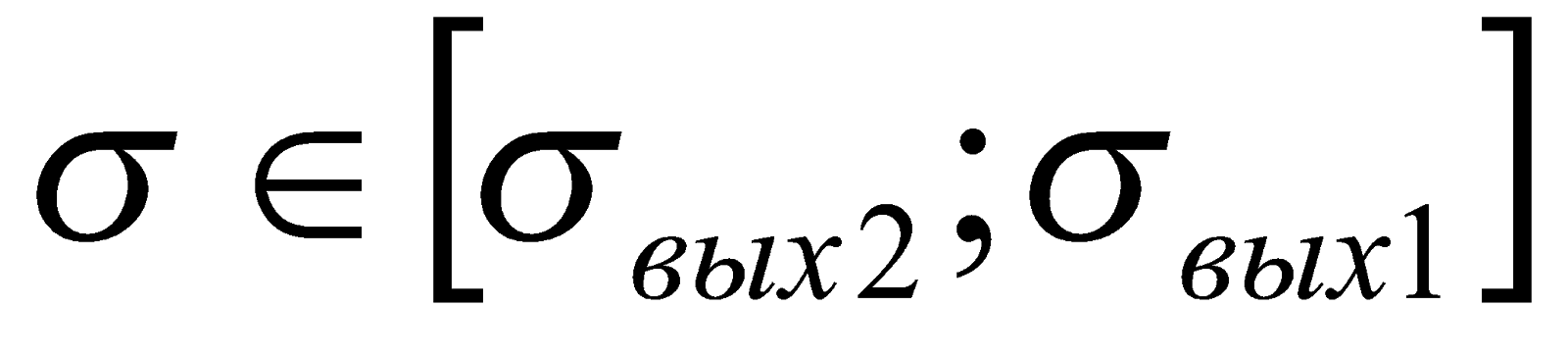 и осуществляется комплексирование;
• фаззификация входных переменных;
• агрегирование подусловий в нечетких правилах продукций;
• агрегирование подзаключений в нечетких правилах продукций по формуле:

,

где  – функция принадлежности терма,  – степень истинности подзаключения;

• аккумуляция заключений нечетких правил продукций по формуле

где D – нечеткое множество, являющееся результатом объединения множеств A и B);

• дефаззификация выходных переменных (расчет координаты ЦТ).

Координаты ЦТ вычисляются по формуле:

 ,

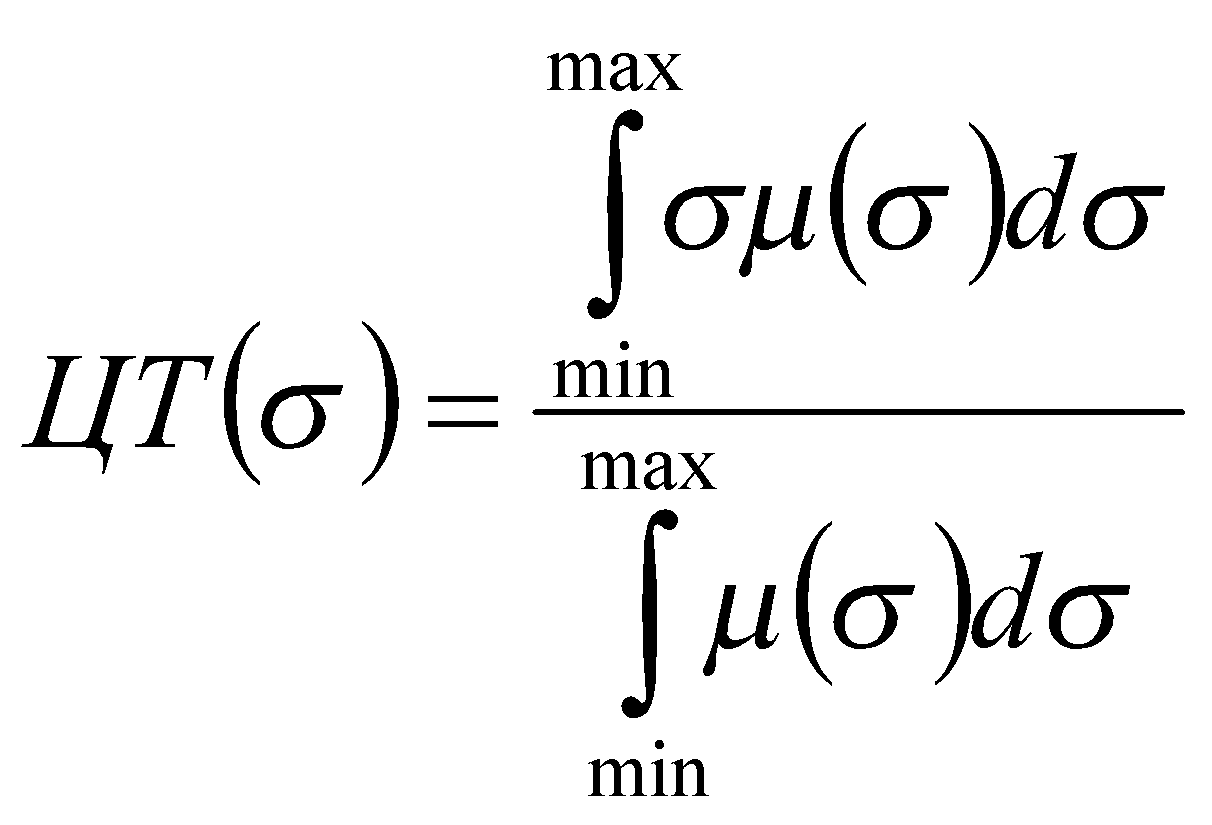где ЦТ(σ) – координата центра тяжести в зависимости от значения нормированного коэффициента (результат дефаззификации);  – функция принадлежности нечеткого множества, соответствующего общему выводу из базы правил.

Для моделирования работы алгоритма использовался модуль нечеткой логики (Fuzzy Logic Toolbox) MATLAB.

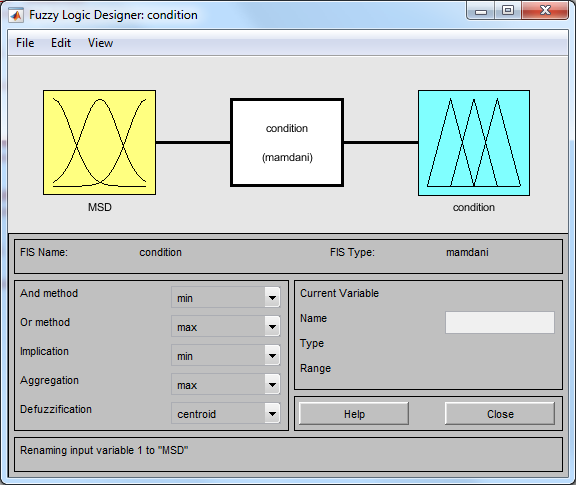
Рис. 3. Общий вид редактора модуля Fuzzy Logix Toolbox

 

В соответствии с рассмотренным выше алгоритмом были заданы:

• входные и выходные нечеткие множества;

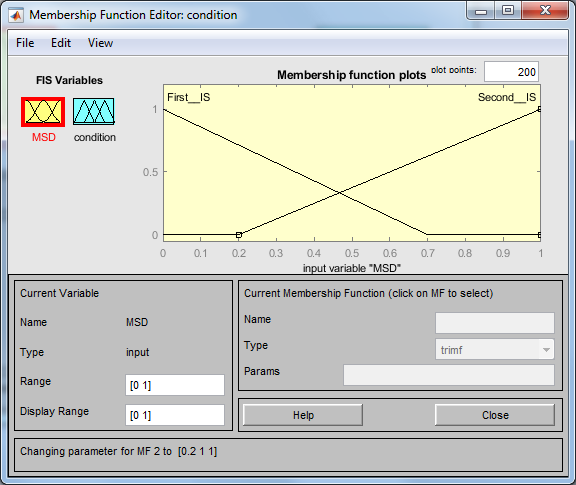
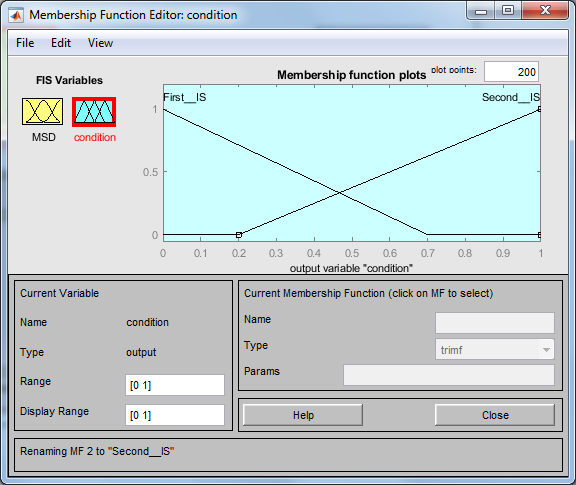
Рис. 4. Входные и выходные функции принадлежности НСВ

• база правил;

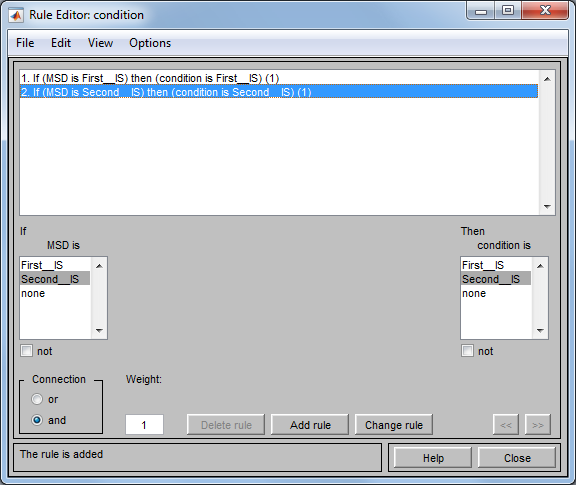
Рис. 5. Редактор базы правил модели вывода

• вычисление координаты ЦТ.

Рис. 6. Окно просмотра результата работы алгоритма нечеткого вывода при 

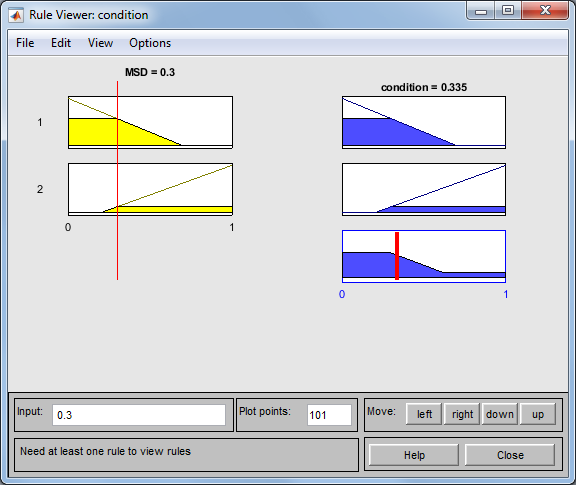
Процесс оценки координат и построение траектории ЦТ(σ) на примере НСВ с одним нормируемым показателем качества представлен на рисунке 7. 

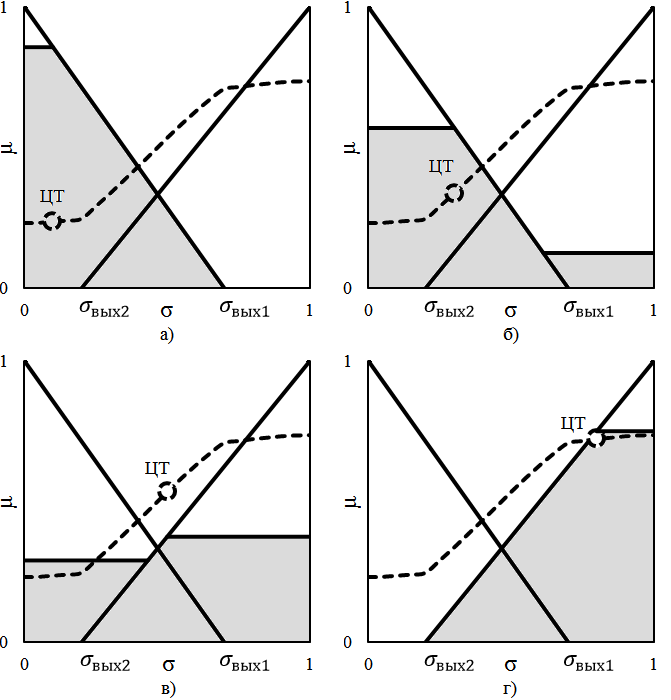
Рис. 7. Построение траектории зависимости ЦТ(σ)

Изменение формы функций принадлежности и областей пересечения функций принадлежности позволяет изменять форму траектории ЦТ с большой вариативностью относительно условий функционирования, специфики работы ИС и т. п., благодаря чему возможно изменение характера весов сигналов ИС: если одна из ИС имеет точность, например, в несколько раз худшую, чем другая, то увеличив участок траектории, который относится к ИС с большей точностью, и участок комплексирования, можно повысить приоритет этих режимов, что физически можно интерпретировать как необходимость пройти больший путь, прежде чем будет осуществлено переключение на другой режим работы.

Для реализации полученного алгоритма в системе реального времени с ограниченными вычислительными ресурсами можно использование заранее рассчитанной траектории ЦТ в виде ломаной, полученной в соответствии с рассматриваемым методом (рис. 8).

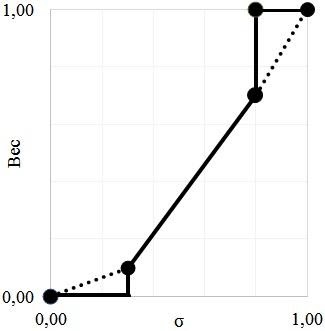
Рис. 8. Траектория ЦТ, использованная при моделировании

Веса первой и второй ИС определяются как:

 ,

На рис. 9 представлены два сигнала: первый сигнал – синус, на который наложен шум с математическим ожиданием 0 и СКО 2 ед., второй сигнал – синус, шум которого имеет параметры 0 и 3 ед. соответственно.

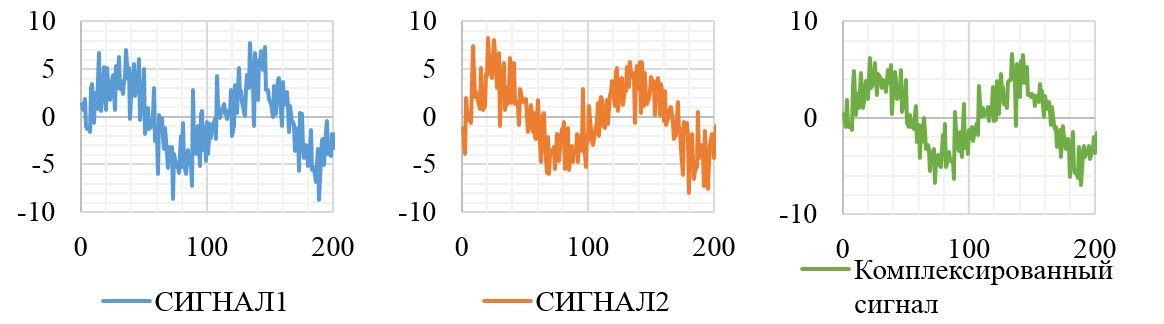
Рис. 9. Два сигнала, представляющие собой зашумленный синус с амплитудой 4 (слева) и сигнал, полученный комплексированием (справа)

СКО комплексированного сигнала равно 1,48 ед., т. е. СКО суммарного сигнала меньше, чем СКО самого точного сигнала от комплексируемых ИС.

 

Выводы

Введение нечеткой логики в процесс комплексирования ИС обеспечивает решение задачи определения границ режимов функционирования ИС и весов сигналов в соответствии с оценками значений координат центра тяжести результирующей функции принадлежности. Комплексирование на основе нечеткой логики позволяет учитывать изменение точности сигналов в зависимости от различных внешних факторов. Проведенное моделирование показало, что комплексирование двух ИС с разными уровнями СКО позволяет получить СКО суммарного сигнала меньшим, чем СКО самой точной комплексируемой ИС.

 

Список литературы

1. Штовба, С. Д. Проектирование нечетких систем средствами MATLAB. – М.: Горячая линия – Телеком, 2007. – 288 с.

2. Пегат, А. Нечеткое моделирование и управление. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2013. – 798 с.

3. Понятский, В. М., Горин, А. В. Комплексирование сигналов от неравноточных информационных систем с помощью нечеткой логики // International Journal of Open Information Technologies. 2019. Т. 7, № 3. С. 25-31.

4. Леоненков, А. В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. – СПб.: БХВ-Петербург, 2003. – 736 с.