Курс "Аналитическая геометрия"

Данный курс "Аналитическая геометрия" рассматриывает следующие темы: геометрические векторы, ориентация пространства, скалярное, векторное и смешанное произведение векторов, уравнения плоскости и прямой в пространстве в декартовой системе координат, различные системы координат на плоскости и в пространстве.

1. Геометрические векторы.

2. Ориентация пространства. Скалярное, векторное и смешанное произведение векторов.

3. Уравнения плоскости и прямой в пространстве в декартовой системе координат.

4. Различные системы координат на плоскости и в пространстве.

Наверх

1. Геометрические векторы.

§ 1. Определения свободного и закрепленного геометрических векторов.

Определение 1: Закрепленный вектор – отрезок с упорядоченными концами: AB, 

A – начало вектора, В – конец вектора, АВ ≠ ВА.

Конец и начало вектора могут совпадать: АА – нулевой вектор.

Определение 2: Равенство закрепленных векторов:

Пусть AB и CD – закрепленные ненулевые векторы.

1) Соединим А с С и В с D (начальные и конечные точки векторов).

Если ABDC – параллелограмм, то AB = CD.

2) AB = CD, если  закрепленный вектор EF : AB = EF и EF = CD.

3) Все нулевые векторы равны: АА = ВВ.

Определение 3: Свободный вектор (или просто вектор) – множество равных между собой (в смысле определения 2) закрепленных векторов.

Свободные векторы обозначаются прописными латинскими буквами – a.

Нулевой свободный вектор обозначается θ.

Определение 4: Закрепленный вектор AB является реализацией свободного вектора a, если a = { CD : CD = AB } ( То есть свободный вектор a – это множество закрепленных векторов CD, т.ч. CD = AB. )

Обозначение: AB  a  (допустимо а = АВ).

Предложение 1. с.в. а и т. О пространства  ! з.в. ОА : ОА  а.

( Т.е. для любого свободного вектора a и для любой точки О пространства существует единственный закреплённый вектор OA, который является реализацией а. )

Определение 5: Длина свободного вектора a – это длина его реализации: 

|a| = |AB|, если AB  a, |θ| = 0.

Определение 6: Угол между свободными векторами а и b – это наименьший угол между их реализациями ОА и ОВ ( ОАа, ОВb ).

Определение 7: Свободные векторы  a и b  равны (a = b), если они совпадают как множества.

Из определения свободного вектора очевидно, что для того, чтобы задать свободный вектор a, достаточно задать какую-либо его реализацию, т.е. закрепленный вектор AB  a.

Определение 8: V3 – множество всех свободных векторов в пространстве R3.

§ 2. Операции над свободными векторами: сложение и умножение на число.

Определение 9: Сумма свободных векторов.

Пусть a, b  V3. Возьмем произвольно точку О.

Тогда ! ОА  a и ! AB  b т.ч. OB  a+b, т.е. a+b = { CD : CD = OB}

Корректность сложения: OB  a+b, O'B'  a+b  OB = O'B'.

Определение 10: Пусть a - свободный вектор, AB – его реализация, тогда BA является реализацией свободного вектора (-a).

(-a) – обратный вектор для a, т.е. (-a) = { BA : AB  a }

Определение 11: Умножение вектора на число:

1) λ•θ = θ для  λ  R.

2) a ≠ θ, AB  a, отрезок AB лежит на прямой l.

2.1) λ = 0  λ∙a = θ.

2.2) λ > 0  AC  λ∙a, где AC т.ч. |AC| = λ•|AB|, C  l и т. B и C находятся по одну сторону от т. А.

2.3) λ < 0  AD  λ∙a, где AD т.ч. |AD| = |λ|∙|AB|, D  l и т. B и D находятся по разные стороны от т. А.

Свойства операций над векторами:   a, b, c  V3 ,   λ, μ  R

1) Коммутативность сложения

a + b = b + a.

2) Ассоциативность сложения

a + b + c = (a + b)+ c = a +( b + c).

3) a + θ = a.

4) a +(-a) = θ.

5) Ассоциативность умножения на число

λ(μ∙ a) = (λμ)∙ a

6) 1∙ a = a.

7) Дистрибутивность умножения на число относительно сложения векторов

λ∙( a + b) = λ∙ a +λ∙ b.

8) Дистрибутивность умножения на число относительно сложения чисел

(λ+μ)∙ a = λ∙ a +μ∙ a.

§ 3. Линейная зависимость векторов. Коллинеарность и компланарность векторов.

Определение 12: Векторы а1, а2, … , аn коллинеарны, если существует прямая l, содержащая реализацию каждого из них.

Обозначение: а || b

Предложение 2: a || b  ó  λ  R, т.ч. a= λ∙b

Определение 13: Коллинеарные векторы  а и b одинаково направлены, если ОАа, ОВb и т. А и В лежат по одну сторону от т. О.

Обозначение: а  b

Определение 14: Коллинеарные векторы  а и b разнонаправлены, если ОАа, ОВb и т. А и В лежат по разные стороны от т. О.

Обозначение: а  b

Определение 15: Векторы а1, а2, … , аn компланарны, если существует плоскость в пространстве, содержащая реализацию каждого из них.

Пример : рассмотрим с.в. еа=а  ( а≠ θ ).

еа коллинеарен  а, одинаково направлен с а, |ea|=1.

Замечание: Любые два свободных вектора компланарны. Нулевой вектор имеет реализацию на любой плоскости в пространстве. Следовательно, три вектора: а, b, θ всегда компланарны.

Определение 16: Система векторов а1, а2, … , аn линейно зависима, если  λ1, λ2, …, λ3 R, не все равные нулю, такие что λ1· а1+ λ2· а2+ λn· аn=0

Определение 17: Если λ1· а1+ λ2· а2+ λn· аn=0 только при λ1 = λ 2 = … = λ3 = 0, то система векторов а1, а2, … , аn линейно независима.

Предложение 3: Любая система из трёх и более ненулевых компланарных векторов линейно зависима.

Предложение 4: Любые три некомпланарных вектора линейно независимы.

§ 4. Проекции закреплённых и свободных векторов на плоскость и прямую.

Проецирование точек на плоскости и прямые хорошо изучается в школьном курсе геометрии, так что остаётся уговориться об обозначениях:

прΠ М; – ортогональная проекция т. М на плоскость Π,

прm М; ( || l ) – проекция т. М на прямую m параллельно прямой l

4.1 Ортогональная проекция на плоскость

Определение 18: Пусть А1= прΠ А, В1= прΠ B A1B1= прΠ AB. 

( Т.е. з.в. A1B1 – это ортогональная проекция з.в. AB на плоскость Π )

Определение 19: Пусть АВ  а и  прΠ AB  а1 а1= прΠ а. 

( Т.е. с.в. а1 – это ортогональная проекция с.в. а на плоскость Π )

4.2 Общий случай проецирования на плоскость. ( Проецирование параллельно прямой l которая не || и не лежит на плоскости Π )

Начало и конец вектора проецируются на Π параллельно l , определения вводятся аналогично п. 4.1 .

4.3 Ортогональная проекция на прямую

Определение 20: Пусть А1= прm А, В1= прm B A1B1= прm AB.]

Определение 21: Пусть АВ  а  и прm AB  а1 а1= прm а. 

4.4 Общий случай проецирования на прямую. ( Проецирование параллельно прямой l которая не || и не совпадает с прямой m)

Начало и конец вектора проецируются на m параллельно l , определения вводятся аналогично п. 4.3 .

§ 5. Базисы в V3. Координаты векторов относительно базиса.

Определение 22: Базисом в пространстве свободных векторов V3 называется любая упорядоченная тройка некомпланарных векторов.

Пусть В : а1, а2, а3 – фиксированный базис в V3.

Определение 23: Координатами вектора b относительно базиса В называется упорядоченная тройка чисел {x, y, z}, т.ч. b=x·a1+ y·а2+z· а3.

Обозначение: b={x, y, z}B

Замечание: Под координатами закреплённого вектора понимают координаты соответствующего ему свободного вектора.

Теорема1: Соответствие между V3 и R3 при фиксированном базисе взаимно однозначно, т.е. b  V3 ! {x, y, z} R3 и {x, y, z} R3 !  b  V3,  т.ч. b={x, y, z}B

Соответствие между вектором и его координатами в данном базисе обладает следующими свойствами:

1. Пусть b1={x1, y1, z1}B, b2={x2, y2, z2}B 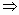  b1+ b2={x1+ x2, y1+ y2, z1+ z2}B

2. Пусть b={x, y, z}B, λ  R λ·b={ λ·x, λ· y, λ·z}B

3. Пусть  b1|| b2, b1= {x1, y1, z1}B, b2={x2, y2, z2}B
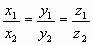     (Здесь:  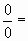любое число).

Определение 24: Ортонормированный ( декартов ) базис – это i, j, k, т.ч.

1) | i |=| j |=| k |=1,

2) i  j  k  i.

Замечание: i, j, k – это стандартное обозначение именно декартова базиса. Т.о., встречая его в тексте можно обойтись без дополнительных пояснений относительно системы координат.

§ 6. Ортогональная система координат в пространстве. Длина вектора. 

Определение 25: Ортогональная ( декартова ) система координат это

1. 1. единица масштаба ( отрезок, длина которого будет считаться "единичной" ),

   2. фиксированная т.О ( начало координат )

   3. ортонормированный базис е1, е2, е3 (изменим стандартное обозначения для удобства)

   4. пересекающиеся в т.О прямые l1, l2, l3, т.ч. li содержит реализацию еi, i=1,2,3.

Если на  li зафиксировать "положительное" направление в соответствии с направлением еi, получим оси координат (стандартное обозначение осей: Ox, Oy и Oz).

Теорема2: Если известны координаты точек А=(x1,y1,z1) и B=(x2,y2,z2) , то координаты вектора АВ можно вычислить по формуле: АВ={ x2-x1 , y2-y1 , z2-z1 }.

Теорема3: Если в ортогональной системе координат b={x, y, z}, то | b |=.

Наверх

2. Ориентация пространства. Скалярное, векторное и смешанное произведение векторов.

§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.

Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями.

Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки.

Определение 1: Упорядоченная тройка некомпланарных векторов а1, а2, а3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а1 к а2 и от а2 к а3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.

Есть и ещё один способ разделить эти два класса:

Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.

Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададимориентацию пространства.

Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого

§ 2. Скалярное произведение векторов.

Определение 2: Скалярное произведение ставит в соответствие паре векторов a и b число (a,b)=|a|·|b|·cosφa,b. 

Свойства скалярного произведения:

1. коммутативность: (a,b)=(b,a) 

2. (а,а)=|а|2

3. (a,b)=0 <=>  a  b

4. Дистрибутивность: (a1+а2,b)= (a1,b)+ (a2,b)

5. (а, λ·b)= λ·(a,b)   λ  R.

Утверждение 1: В декартовом базисе если а={x1,y1,z1}, b={x2,y2,z2}, то (a,b)=x1·x2+y1·y2+z1·z2.

§ 3. Векторное произведение векторов.

Определение 3: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что

1. | [a,b] |=Sa,b, где Sa,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то Sa,b=0.)

2. a [a,b] b.

3. a, b, [a,b] – правая тройка.

Свойства векторного произведения:

1. [a,b] = -[b,a]

2. [a,b] = θ  ó a || b

3. [a1+a2,b] = [a1,b]+[a2,b]

4. λ·[a,b] = [λ·a,b] = [a,λ·b]   λ R.

Утверждение 2: В декартовой системе координат (базис i, j, k), a={x1, y1, z1},  b={x2, y2, z2} 

=> [a,b] =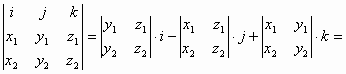

=

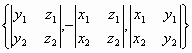
§4. Смешанное произведение векторов.

Определение 4: Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).

Утверждение 3: <a,b,c>=Va,b,c, если a,b,c – правая тройка, или <a,b,c>= -Va,b,c, если a,b,c – левая тройка. Здесь Va,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.)

Утверждение 4: В декартовой системе координат, если a={x1, y1, z1},  b={x2, y2, z2}, 

с={x3, y3, z3}, => <a,b,c>=.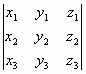

Наверх

3. Уравнения плоскости и прямой в пространстве в декартовой системе координат.

§ 1. Каноническое уравнение плоскости в пространстве

Пусть в декартовой системе координат дан вектор n={A,B,C} и точка М0=(x0,y0,z0).

Построим плоскость Π, проходящую через т. М0, перпендикулярную вектору n (этот вектор называютнормальным вектором или нормалью плоскости).

Утверждение 1: М  Π  ó  М0М n.

М0М={x-x0, y-y0, z-z0}   n  ó  A(x-x0)+B(y-y0)+C(z-z0)=0. (*)

(См. свойства скалярного произведения)

• Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0.

Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости. 

§ 2. Канонические и параметрические уравнения прямой в пространстве

Пусть в декартовой системе координат дан вектор a={p,q,r} и точка М0=(x0,y0,z0).

Построим прямую l, проходящую через т. М0, параллельную вектору a (этот вектор называютнаправляющим вектором прямой).

Утверждение 2: М l  ó М0М || a.

М0М={x-x0, y-y0, z-z0} || a  ó  tR, т.ч. М0М=t·a  =>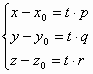  

• Параметрические уравнения прямой в пространстве:

(**)

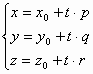Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем. 

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t0=0 он находится в точке М0, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**). 

Теперь несколько преобразуем формулы (**). 

Выразим из каждой строчки параметр t: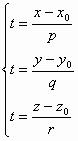

• Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения. 

Замечание 3: Это формальная запись и выражение вида  в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

§3. Расстояние от точки до плоскости в пространстве

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М1=(x1,y1,z1).

Утверждение 3: расстояние от точки М1 до плоскости Π вычисляется по формуле:

§4. Координаты точки, делящей отрезок в заданном соотношении

Пусть в декартовой системе координат М1=(x1,y1,z1), М2=(x2,y2,z2) .

Утверждение 4: Координаты т. М, т.ч. М1М=λ∙ММ2, находятся по следующим формулам: 

.

Наверх

4. Различные системы координат на плоскости и в пространстве.

§ 1. Декартова система координат на плоскости

Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.

Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.

Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.

Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).

§ 2. Полярная система координат на плоскости

Для того, чтобы задать полярную систему координат на плоскости, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.

Положение точки на плоскости задаётся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.

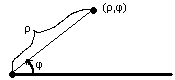
Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ0.

Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то 

x = ρ∙cosφ, 

y = ρ∙sinφ.

В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.

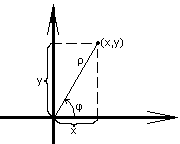
С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..

В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.

§3. Декартова система координат в пространстве

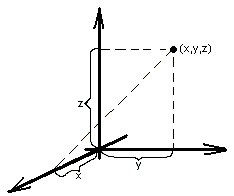
Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.

§4. Цилиндрическая система координат в пространстве

Цилиндрическая система координат в пространстве – “родственница” полярной системы координат на плоскости. Чтобы получить цилиндрическую систему надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. Т.о., координаты точки – три числа: первые два – полярные координаты проекции нашей точки на плоскость, третье – величина проекции точки на вертикальную ось. 

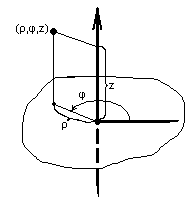
Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:

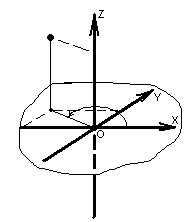
x = ρ·cosφ,

y = ρ·sinφ,

z = z.

§5. Сферическая система координат в пространстве

Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней -- точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.

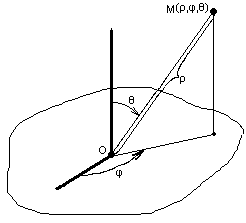
Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:

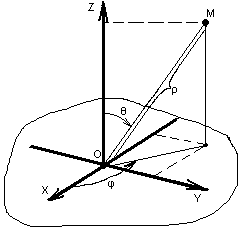
x = ρ·sinθ·cosφ,

y = ρ·sinθ·sinφ,

z = ρ·cosθ.