Курс "Обыкновенные дифференциальные уравнения"
В данной публикации представлен курс "Обыкновенные дифференциальные уравнения".
1. Обыкновенные дифференциальные уравнения 1 порядка. Основные понятия
2. Численное решение задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка
3. Дифференциальное уравнение первого порядка с разделяющимися переменными
4. Дифференциальные уравнения первого порядка в полных дифференциалах
5. Линейные дифференциальные уравнения первого порядка. Метод вариации произвольных постоянных
6. Дифференциальные уравнения высших порядков
7. Системы обыкновенных дифференциальных уравнений
8. Линейные дифференциальные уравнения
9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
10. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
12. Автономные системы на плоскости. Фазовая плоскость. Векторное поле
13. Точки покоя автономной линейной системы
14. Автономные системы на плоскости. Предельные циклы
15. Жесткие системы дифференциальных уравнений
16. Решение задачи Коши операционным методом
17. Приложения обыкновенных дифференциальных уравнений к задачам биологии и экономики
1. Обыкновенные дифференциальные уравнения 1 порядка. Основные понятия
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
F(x, y, y' )=0,
где F — известная функция трех переменных, определенная в области G из R3, x — независимая переменная из интервала (a, b), y(x) — неизвестная функция, y'(x) — ее производная.
Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида
y'=f(x, y)
называют уравнениями в нормальной форме.
Функция y=y(x) называется решением дифференциального уравнения, если она непрерывно дифференцируема на (a, b) и при всех x из (a, b) удовлетворяет уравнению F(x, y(x), y'(x))=0.
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Для дифференциального уравнения y'=f(x, y), правая часть которого f(x, y) и ее частная производная по y непрерывны в некоторой области D имеет место геометрическая интерпретация, называемая полем направлений.
Если через каждую точку (x, y) области D провести некоторый отрезок l(x, y) с угловым коэффициентом, равным значению правой части f(x, y) в точке (x, y), то получится изображение, которое называется "полем направлений". Любая интегральная кривая y=y(x) в каждой своей точке (x, y(x)) касается отрезка l(x, y).
Если дифференциальное уравнение первого порядка y'=f(x, y), имеет решение, то решений у него, вообще говоря, бесконечно много и эти решения могут быть записаны в виде y=y(x,C), где C — произвольная константа.
Выражение y(x,C) называют общим решением дифференциального уравнения 1-го порядка:
при всех допустимых значениях C функция y=y(x,C) является решением уравнения,
y'(x,C)=f(x, y(x, C));
для любого наперед заданного решения y=f(x) найдется такое значение константы C, C=С*, что y(x,C*)=f(x).
Однако, если поставить задачу: найти решение, удовлетворяющее условию y(x0)=y0, то при определенных условиях такая задача имеет единственное решение. Задача об отыскании решения y=y(x) дифференциального уравнения y'=f(x, y), удовлетворяющего начальному условию y(x0)=y0, называется задачей Коши. Решение задачи Коши называют частным решением.
Справедлива следующая теорема существования и единственности решения задачи Коши.
Если функция f(x, y) и ее частная производная по y непрерывны в области D, (x0, y0)ОD, то на некотором интервале (x0-h, y0+h) существует единственное решение y=y(x) уравнения y'=f(x, y), удовлетворяющее начальному условию y(x0)=y0.
Теорема существования и единственности имеет простую геометрическую интерпретацию: если условия теоремы выполнены в области D, то через каждую точку (x0, y0)ОD проходит только одна интегральная кривая y=y(x,C0) семейства y=y(x,C) такая, что y(x0,C0)=y0.
2. Численное решение задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка
Если задачу об отыскании всех решений дифференциального уравнения удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что уравнение интегрируется в квадратурах. В приложениях крайне редко встречаются уравнения, интегрируемые в квадратурах. Поэтому для исследования дифференциальных уравнений широко используются приближенные, численные методы их решения.
Численное решение на отрезке [a, b] задачи Коши
y' = f(x, y), y(a) = y0
состоит в построении таблицы приближенных значений
y0, y1, ..., yi, ... yN
решения y(x) в узлах сетки
a=x0 < x1 < ... < xi < ...< xN=b, y(xi)@ yi.
Если xi = a+ i h, h=(b-a)/ N, то сетка ![]() называется равномерной.
называется равномерной.
Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке x0 + h используется информация о решении только в точке x0.
Простейший одношаговый метод численного решения задачи Коши - метод Эйлера. В методе Эйлера величины yi вычисляются по формуле
yi+1 = yi + h f(xi , yi), i = 0, 1, ...
Метод Эйлера допускает простую геометрическую интерпретацию. Пусть известна точка (xi, yi) интегральной кривой уравнения y'=f(x, y).
Касательная к интегральной кривой уравнения, проходящая через эту точку, определяется уравнением
y = yi + f(xi , yi)(x-xi).
Следовательно, вычисленная методом Эйлера точка (xi+1 , yi+1 ),
где xi+1=xi+h, yi+1=yi + h f(xi , yi), лежит на этой касательной.
Методом Рунге-Кутты четвертого порядка точности называют одношаговый метод, относящийся к широкому классу методов Рунге-Кутты. В этом методе величины yi+1 вычисляются по следующим формулам:
yi+1 = yi + h (k1 + 2k2 + 2k3 + k4)/6 , i = 0, 1, ...
k1 = f(xi , yi),
k2 = f(xi+h/2, yi+hk1/2),
k3 = f(xi+h/2, yi+hk2/2),
k4 = f(xi+h, yi+hk3).
Практически оценить погрешность численного метода позволяет правило Рунге. Сначала вычисляют приближенное решение с шагом h, затем - с шагом h/2. Тогда для метода Рунге-Кутты 4 порядка точности справедливо приближенное равенство
y(x2i) - y2i(h/2) @ (y2i(h/2) - yi(h))/15,
здесь yi(h) - приближенное решение, вычисленное с шагом h,
y2i(h/2) - приближенное решение, вычисленное с шагом h/2.
За оценку погрешности решения, вычисленного с шагом h/2, принимают величину
maxi|y2i(h/2) - yi(h) |/15.
3. Дифференциальное уравнение первого порядка с разделяющимися переменными
Уравнением с разделяющимися переменными называется уравнение первого порядка вида
![]()
где X(x) и Y(y) — непрерывные функции.
Общий интеграл уравнения задается выражением
![]()
Решение y = y(x) задачи Коши y(x0) = y0 как неявную функцию переменной x задает выражение
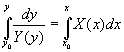
Заметим, что если Y(y*) = 0 в некоторой точке y*, то уравнение
y' = Y(y)X(x) имеет решение y(x) = y* при всех допустимых x.
Все решения системы исчерпываются выражениями y(x) = y* и
.gif)
4. Дифференциальные уравнения первого порядка в полных дифференциалах
Обыкновенное дифференциальное уравнение первого порядка вида
P(x, y) dx + Q(x, y) dy = 0
называется уравнением в полных дифференциалах, если P(x, y) и Q(x, y) непрерывны в некоторой односвязной области D и в этой области выполнено условие
![]()
Тогда общий интеграл уравнения задается выражением
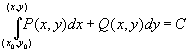 .
.
Обозначим
![]()
тогда
![]()
откуда
![]()
и формула для вычисления u(x, y) имеет вид:
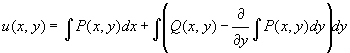
Выражение u(x, y)=0, где
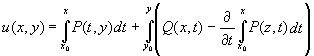
задает решение задачи Коши y(x0) = y0.
5. Линейные дифференциальные уравнения первого порядка. Метод вариации произвольных постоянных
Уравнение вида
![]()
называется линейным неоднородным уравнением.
Уравнение вида
![]()
называется линейным однородным уравнением.
Очевидно, что однородное линейное уравнение является уравнением с разделяющимися переменными и его общее решение вычисляется по формуле
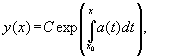
где C— произвольная постоянная,
Решение задачи Коши y(x0) = y0 определяется выражением

Метод вариации произвольных постоянных для линейного неоднородного уравненя состоит в том, что решение неоднородного уравнения записывается в виде

где C(x) неизвестная функция. Подставляя в уравнение имеем для C(x) 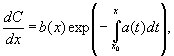
откуда
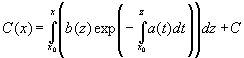
и тогда для общего решения неоднородного уравнения справедливо
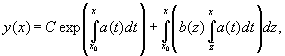
где C — произвольная постоянная.
Для решения задачи Коши y(x0) = y0 для линейного неоднородного уравнения справедлива формула
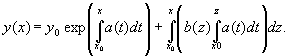
6. Дифференциальные уравнения высших порядков
Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида
F(x, y, y', y'', ..., y(n)) = 0,
где F - известная функция (n+2) переменных, определенная в области D М Rn+2, x - независимая переменная из интервала (a, b), y = y(x) - неизвестная функция, n - порядок уравнения.
В дальнейшем будем рассматривать обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной - уравнения, записанные в нормальной форме:
y(n)) = f(x, y, y', y'', ..., y(n-1)).
Функция y(x) называется решением дифференциального уравнения n-го порядка, если она n раз непрерывно дифференцируема на промежутке (a, b) и удовлетворяет уравнению для всех
xО(a, b).
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Дифференциальное уравнение n-го порядка имеет, вообще говоря, бесконечное множество решений. Чтобы выделить единственное решение уравнения достаточно определить начальные условия:
y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1.
При определенных ограничениях на правую часть уравнения эта задача, она называется задачей Коши, имеет единственное решение.
Справедлива следующая теорема существования и единственности решения задачи Коши.
Если правая часть уравнения
y(n)) = f(x, y, y', y'', ..., y(n-1))
и ее частные производные по переменным y, y', y'', ..., y(n-1) непрерывны в области GМ Rn+1, то для любой точки (x0, y0, y0,1, y0,2, ..., y0,n-1) из G на некотором интервале (x0-h, x0+h) существует единственное решение y(x) уравнения, удовлетворяющее начальным условиям
y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1.
Численное решение задачи Коши
y(n)) = f(x, y, y', y'', ..., y(n-1)),
y(x0) = y0 , y'(x0) = y0,1 , y''(x0) = y0,2 , ..., y(n-1)(x0) = y0,n-1
состоит в построении таблицы приближенных значений yi решения y=y(x) в точках x1, x2, ..., xi, ... .
Задача о численном решении дифференциального уравнения порядка выше первого чаще всего сводится к численному решению решению задачи Коши для нормальной системы дифференциальных уравнений.
Обозначив
y(x)=y1(x), y'(x)=y2(x), y''(x)=y3(x), ..., y(n-1)(x)=yn (x),
получим задачу Коши для системы n дифференциальных уравнений 1-го порядка
y1'=y2 , y2'=y3 , ..., yn' =f(x, y1, y2 , ..., yn ),
y1(x0 )=y0, y2(x0)=y1,0 , ..., yn-1(x0)=yn-1,0,
которая в векторной форме имеет вид
`Y '= `F(x,`Y), `Y(x0) =`Y0,
`Y (x)=(y1(x), y2(x), ..., yn(x)), `Y '(x)=(y1'(x), y2'(x), ..., yn'(x)),
`F(x,`Y)= (y2, y3, ..., yn, f(x, y1, y2 , ..., yn )).
Численное решение задачи Коши для этой системы состоит в построении таблицы приближенных значений yi,1 , yi,2 , ..., yi,N компонент yi(xj) вектора решения в точках x1 , x2 , ..., xN. Чтобы получить расчетные формулы метода Рунге—Кутты для систем дифференциальных уравнений, достаточно в расчетных формулах для уравнений первого порядка заменить
y, f(x, y), k1, k2, k3, k4 на `Y, `F(x,`Y), `k1, `k2, `k3, `k4 .
7. Системы обыкновенных дифференциальных уравнений
Рассмотрим систему дифференциальных уравнений
y'1 = f1(x, y1, y2 , ..., yn),
y'2 = f2 (x, y1, y2 , ..., yn),
..............................
y'n = fn (x, y1, y2 , ..., yn),
где x — независимая переменная, а
y1(x), y2(x), ..., yn(x) — неизвестные функции, n — порядок системы.
Обозначив
.gif)

запишем систему в векторной форме
`Y '=`F(x,`Y ).
Решением системы называется вектор-функция `Y , которая определена и нерерывно дифференцируема на интервале (a, b) и удовлетворяет системе, т.е. для всех x0О (a, b) справедливо
`Y '(x) =`F(x,`Y (x)).
Задачей Коши (задачей с начальными условиями) называется следующая задача: найти такое решение`Y (x) системы `Y '=`F(x,`Y ), что `Y (x0) =`Y 0,
где x0 — заданное число, а `Y 0 — заданный вектор.
Интегральной кривой системы называется кривая в (n+1) -мерном пространстве Rn+1x,y, заданная уравнением `Y =`Y (x), где `Y (x) - решение системы.Таким образом, решить задачу Коши — это значит найти интегральную кривую, проходящую через заданную точку пространства Rn+1x,y.
Для нормальных систем обыкновенных дифференциальных уравнений справедлива следующая теорема существования и единственности решения задачи Коши.
Если вектор-функция `F(x,`Y (x)) и ее частные производные по переменным yi , i = 1, 2, ..., n, непрерывны в области G пространства Rn+1x,y, то на некотором интервале (x0 -h, x0+h) существует единственное решение системы
`Y '(x) =`F(x,`Y (x)) ,
удовлетворяющее начальному условию
`Y (x0) =`Y 0,
т.е. через каждую точку области G проходит единственная интегральная кривая системы.
Подробнее геометрическая интерпретация систем обыкновенных дифференциальных уравнений и их решений рассмотрена в разделе, посвященном изучению автономных систем.
Если задачу об отыскании всех решений системы дифференциальных уравнений удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что система интегрируется в квадратурах.
В приложениях крайне редко встречаются системы, интегрируемые в квадратурах. Поэтому для исследования дифференциальных уравнений широко используются приближенные, численные методы их решения.
Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений состоит в построении таблицы приближенных значений
yi,1, yi,2 , ..., yi,N компонент yi(xj,) вектора решения `Y (x) в точках
x1, x2 , ..., xN.
Чтобы получить расчетные формулы метода Рунге—Кутты для систем дифференциальных уравнений, достаточно в расчетных формулах для уравнений первого порядка заменить
y, f(x, y), k1, k2, k3 , k4 на
`Y , F(x,`Y ), `k 1, `k 2, `k 3, `k 4.
Задача Коши для любого дифференциального уравнения n -го порядка
y(n) = f(x, y' , y' , ..., y(n-1)),
y(x0 )= y0 , y'(x0 )= y0,1, y''(x0 )= y0,2 , ..., y(n-1)(x0 )= y0,n-1
легко сводится к задаче для системы дифференциальных уравнений порядка
`Y '=`F(x,`Y ), где
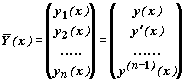
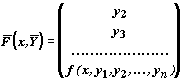

8. Линейные дифференциальные уравнения
Линейным дифференциальным уравнением n -го порядка называется уравнение вида
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x),
где y = y(x) — неизвестная функция,
a1(x), a2(x), ..., an-1(x), an(x), f(x) — известные функции, которые будем полагать непрерывными на промежутке (a, b).
Выражение в левой части уравнения называется линейным дифференциальным оператором n -го порядка:
L(y) = y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y .
Уравнения
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = 0 и
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x), f(x) № 0,
называются соответственно однородным и неоднородным линейным дифференциальным уравнением n -го порядка.
Будем записывать однородное и неоднородное линейные дифференциальные уравнения в виде:
L(y) = 0 и L(y) = f(x).
Принцип суперпозиции основан на следующих свойствах решений линейных уравнений:
а) Если y1(x) и y2(x) — два решения однородного линейного уравнения L(y)=0, то их линейная комбинация y(x) = c1 y1(x) + c2 y2(x)
при любых постоянных c1, c2 является решением однородного уравнения.
б) Если y1(x) и y2(x) — два решения неоднородного линейного уравнения
L(y) = f(x), то их разность y(x) = y1(x) - y2(x)
является решением однородного уравнения L(y) = 0.
в) Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма частного (фиксированного) решения неоднородного уравнения и некоторого решения однородного уравнения.
Принцип суперпозиции:
Если y1(x) и y2(x) — решения неоднородных линейных уравнений
L(y) = f1(x) и L(y) = f2(x), то их сумма y(x) = y1(x) + y2(x) является решением уравнения
L(y) = f1(x) + f2(x).
9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Для линейного однородного дифференциального уравнения n-го порядка
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = 0,
где y = y(x) — неизвестная функция, a1(x), a2(x), ..., an-1(x), an(x) — известные, непрерывные, справедливо:
1) существуют n линейно независимых решений уравнения
y1(x), y2(x), ..., yn(x);
2) при любых значениях констант c1, c2, ..., cn функция
y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x)
является решением уравнения;
3) для любых начальных значений x0, y0, y0,1, ..., y0,n-1 существуют такие значения c*1, c*n, ..., c*n, что решение
y*(x)=c*1 y1(x) + c*2 y2(x) + ... + c*n yn (x)
удовлетворяет при x = x0 начальным условиям
y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
Выражение y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) называется общим решением линейного однородного дифференциального уравнения n-го порядка.
Совокупность n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка y1(x), y2(x), ..., yn(x) называется фундаментальной системой решений уравнения.
Для линейного однородного дифференциального уравнения с постоянными коэффициентами существует простой алгоритм построения фундаментальной системы решений. Будем искать решение уравнения в виде y(x) = exp(lx):
exp(lx)(n) + a1exp(lx)(n-1) + ... + an-1exp(lx)' + anexp(lx)=
= (ln + a1ln-1 + ... + an-1l + an)exp(lx) = 0,
т.е. число l является корнем характеристического уравнения
ln + a1ln-1 + ... + an-1l + an = 0.
Левая часть характеристического уравнения называется характеристическим многочленом линейного дифференциального уравнения:
P(l) = ln + a1ln-1 + ... + an-1l + an.
Таким образом, задача о решении линейного однородного уравнения n -го порядка с постоянными коэффициентами сводится к решению алгебраического уравнения.
Если характеристическое уравнение имеет n различных действительных корней
l1№ l2 № ... № ln,
то фундаментальная система решений состоит из функций
y1(x) = exp(l1x), y2(x) = exp(l2x), ..., yn(x) = exp(lnx),
и общее решение однородного уравнения имеет вид:
y(x)= c1 exp(l1x) + c2 exp(l2x) + ... + cn exp(lnx).
Если какой-либо из действительных корней характеристического уравнения повторяется r раз (r-кратный корень), то в фундаментальной системе решений ему отвечают r функций; если
lk=lk+1 = ... = lk+r-1,
то в фундаментальную систему решений уравнения входят r функций:
yk(x) = exp(lkx),
yk+1(x) = xexp(lkx),
yk+2(x) = x2exp(lkx), ...,
yk+r-1(x) =xr-1 exp(lnx).
Если характеристическое уравнение имеет комплексные корни, то каждой паре простых (имеющих кратность 1 ) комплексных корней
lk,k+1=ak ± ibk
в фундаментальной системе решений отвечает пара функций
yk(x) = exp(akx)cos(bkx), yk+1(x) = exp(akx)sin(bkx).
Если же комплексная пара корней имеет кратность r, то такой паре
lk=lk+1 = ... = l2k+2r-1=ak ± ibk,
в фундаментальной системе решений отвечают функции
exp(akx)cos(bkx), exp(akx)sin(bkx),
xexp(akx)cos(bkx), xexp(akx)sin(bkx),
x2exp(akx)cos(bkx), x2exp(akx)sin(bkx),
................
xr-1exp(akx)cos(bkx), xr-1exp(akx)sin(bkx).
Таким образом, для отыскания общего решения линейного однородного дифференциального уравнения с постоянными коэффициентами следует:
записать характеристическое уравнение;
найти все корни характеристического уравнения l1, l2, ... , ln;
записать фундаментальную систему решений y1(x), y2(x), ..., yn(x);
записать выражение для общего решения y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x).
Для решения задачи Коши нужно подставить выражение для общего решения в начальные условия и определить значения постоянных c1,..., cn, которые являются решениями системы линейных алгебраических уравнений
c1 y1(x0) + c2 y2(x0) + ... + cn yn(x0) = y0,
c1 y'1(x0) + c2 y'2(x0) + ... + cn y'n(x0) =y0,1,
......... ,
c1 y1(n-1)(x0) + c2 y2(n-1)(x0) + ... + cn yn(n-1)(x0) = y0,n-1
10. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Для линейного неоднородного дифференциального уравнения n-го порядка
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x),
где y = y(x) — неизвестная функция, a1(x), a2(x), ..., an-1(x), an(x), f(x) — известные, непрерывные,справедливо:
1) если y1(x) и y2(x) — два решения неоднородного уравнения, то функция
y(x) = y1(x) - y2(x) — решение соответствующего однородного уравнения;
2) если y1(x) решение неоднородного уравнения, а y2(x) — решение соответствующего однородного уравнения, то функция
y(x) = y1(x) + y2(x) — решение неоднородного уравнения;
3) если y1(x), y2(x), ..., yn(x) — n линейно независимых решений однородного уравнения, а yч(x) — произвольное решение неоднородного уравнения,
то для любых начальных значений
x0, y0, y0,1, ..., y0,n-1
существуют такие значения
c*1, c*n, ..., c*n, что решение
y*(x)=c*1 y1(x) + c*2 y2(x) + ... + c*n yn (x) + yч(x)
удовлетворяет при x = x0 начальным условиям
y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
Выражение
y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x)
называется общим решением линейного неоднородного дифференциального уравнения n-го порядка.
Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида:
Pk(x)exp(ax)cos(bx) + Qm(x)exp(ax)sin(bx),
где Pk(x), Qm(x) — многочлены степени k и m соответственно, существует простой алгоритм построения частного решения, называемый методом подбора.
Метод подбора, или метод неопределенных коэффициентов, состоит в следующем.
Искомое решение уравнения записывается в виде:
(Pr(x)exp(ax)cos(bx) + Qr(x)exp(ax)sin(bx))xs,
где Pr(x), Qr(x) — многочлены степени r = max(k, m) с неизвестными коэффициентами
pr , pr-1, ..., p1, p0, qr, qr-1, ..., q1, q0.
Сомножитель xs называют резонансным сомножителем. Резонанс имеет место в случаях, когда средикорней характеристического уравнения есть корень
l =a ± ib кратности s.
Т.е. если среди корней характеристического уравнения соответствующего однородного уравнения есть такой, что его действительная часть совпадает с коэффициентом в показателе степени экспоненты, а мнимая — с коэффициентом в аргументе тригонометрической функции в правой части уравнения, и кратность этого корня s, то в искомом частном решении присутствует резонансный сомножитель xs. Если же такого совпадения нет (s=0), то резонансный сомножитель отсутствует.
Подставив выражение для частного решения в левую часть уравнения, получим обобщенный многочлен того же вида, что и многочлен в правой части уравнения, коэффициенты которого неизвестны.
Два обобщенных многочлена равны тогда и только тогда, когда равны коэффициенты при сомножителях вида xtexp(ax)sin(bx), xtexp(ax)cos(bx) с одинаковыми степенями t.
Приравняв коэффициенты при таких сомножителях, получим систему 2(r+1) линейных алгебраических уравнений относительно 2(r+1) неизвестных. Можно показать, что такая система совместна и имеет единственное решение.
Таким образом, для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует
найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения l1, l2, ... , ln, записать фундаментальную систему решений y1(x), y2(x), ..., yn(x));
найти любое частное решение неоднородного уравнения yч(x);
записать выражение для общего решения
y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x);
Для решения задачи Коши нужно подставить выражение для общего решения в начальные условия и определить значения постоянных c1,..., cn, которые являются решениями системы линейных алгебраических уравнений
c1 y1(x0) + c2 y2(x0) + ... + cn yn(x0) + yч(x0)= y0,
c1 y'1(x0) + c2 y'2(x0) + ... + cn y'n(x0) + yч(x0)=y0,1,
......... ,
c1 y1(n-1)(x0) + c2 y2(n-1)(x0) + ... + cn yn(n-1)(x0) + yч(x0)= y0,n-1
11. Метод вариации произвольных постоянных решения задачи Коши для линейного неоднородные дифференциального уравнения с постоянными коэффициентами
Доказано, что для линейного неоднородного дифференциального уравнения
y(n) + a1 y(n-1) + ... + an-1 y' + an y = f(x)
при непрерывной правой части f(x), для любых начальных значений
x0, y0, y0,1, ..., y0,n-1
существует и единственно решение задачи Коши
y(x0)=y0, (y)'(x0)=y0,1 , ...,(y)(n-1)(x0)=y0,n-1.
Решение задачи Коши для неоднородного дифференциального уравнения с постоянными коэффициентами можно найти методом вариации произвольных постоянных (методом Лагранжа), который состоит в следующем:
Записываем искомое решение задачи Коши для неоднородного уравнения в виде
y(x)= c1(x) y1(x) + c2(x) y2(x) + ... + cn(x) yn(x),
где y1(x), y2(x), ..., yn(x) — линейно независимые решения соответствующего однородного уравнения, и находим неизвестные функции
c1(x) , c2(x), ..., cn(x),
такие, чтобы функция y = y(x) удовлетворяла неоднородному уравнению и заданным начальным условиям.
Опишем алгоритм решения задачи Коши для уравнения второго порядка
y'' + a1 y' + a2 y = f(x), y(x0)=y0, (y)'(x0)=y0,1.
Будем искать решение задачи в виде
y(x)= c1(x) y1(x) + c2(x) y2(x),
где y1(x), y2(x) — линейно независимые решения однородного уравнения
y'' + a1 y' + a2 y = 0.
Вычислим y'(x), y''(x) и подставим полученные выражения в уравнение.
Вычислим первую производную
y'(x)= (c1'(x) y1(x) + c2(x)' y2(x)) + (c1(x) y1'(x) + c2(x) y2'(x)),
положим
c1'(x) y1(x) + c2(x)' y2(x) = 0
и тогда
y'(x)= c1(x) y1'(x) + c2(x) y2'(x),
y''(x)= (y'(x))'= (c1(x) y1'(x) + c2(x) y2'(x))'=
=c1'(x) y1'(x) + c2(x)' y2'(x) + c1(x) y1''(x) + c2(x) y2''(x).
Подставив y(x) и ее производные в уравнение, получим:
y'' + a1 y' + a2 y =
= c1'(x) y1'(x) + c2(x)' y2'(x) + c1(x) y1''(x) + c2(x) y2''(x) +
+ a1(c1(x) y1'(x)+c2(x) y2'(x)) + a2(c1(x) y1(x)+c2(x) y2(x)) =
= c1(x)( y1''(x)+a1 y1'(x)+a2 y1(x)) + c2(x)( y2''(x)+a1 y2'(x)+a2 y2(x)) +
+ c1'(x) y1'(x) + c2(x)' y2'(x) = 0 + 0 + c1'(x) y1'(x) + c2(x)' y2'(x) = f(x),
при условии c1'(x) y1(x) + c2(x)' y2(x) = 0.
Тогда неизвестные функции c1(x) и c2(x) являются решениями системы линейных дифференциальных уравнений
c1'(x) y1'(x) + c2(x)' y2'(x) = f(x),
c1'(x) y1(x) + c2(x)' y2(x) = 0
с известными y1(x) и y2(x).
Эта система легко разрешима относительно c1(x) и c2(x):
c1'(x) = f(x)y2(x)/(y1'(x)y2(x)-y1(x)y2'(x)),
c1'(x)= f(x)y1(x)/(y1(x)y2'(x)-y1'(x)y2(x)).
Вычислив интегралы в правой части системы, получим
![]()
![]()
Произвольные константы C1 и C2 определяются из начальных условий.
Заметим, что разрешимость системы дифференциальных уравнений для
c1'(x) и c2'(x) и однозначная разрешимость системы начальных условий для произвольных констант C1 и C2 гарантированы линейной независимостью y1(x) и y2(x),
(y1'(x)y2(x)-y1(x)y2'(x))№0 для линейно независимых y1(x) и y2(x).
Для того чтобы решить задачу Коши для уравнения более высокого порядка действуем аналогично.
Решение задачи Коши ищем в виде
y(x)= c1(x) y1(x) + c2(x) y2(x) + ... + cn(x) yn(x),
где y1(x), y2(x), ..., yn(x) — линейно независимые решения соответствующего однородного уравнения.
Неизвестные функции c1(x) , c2(x), ..., cn(x)
находим как решения линейной системы дифференциальных уравнений
c1'(x) y1(x) + c2(x)' y2(x) + ... + cn'(x) yn(x) = 0
c1'(x) y1'(x) + c2'(x) y2'(x) + ... + cn'(x) yn'(x) = 0,
c1'(x) y1''(x) + c2'(x) y2''(x) + ... + cn'(x) yn''(x) = 0,
.................
c1'(x) y1(n-1)(x) + c2'(x) y2(n-1)(x) + ... + cn'(x) yn(n-1)(x) = f(x),
которая в силу линейной независимости y1(x), y2(x), ..., yn(x) разрешима относительно ci'(x).
Вычислив ci(x) = Fi(x) + Ci находим произвольные постоянные Ci из начальных условий и тогда искомое решение уравнения имеет вид
y(x)= F1(x) y1(x) + F2(x) y2(x) + ...+ Fn(x) yn(x) + C1y1(x) + C2 y2(x) +...+ Cnyn(x).
Таким образом, для того чтобы решить методом вариации произвольных постоянных решение задачи Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует:
записать характеристическое уравнение;
найти все корни характеристического уравнения l1, l2, ... , ln;
найти фундаментальную систему решений y1(x), y2(x), ..., yn(x));
представить искомое решение задачи Коши в виде линейной комбинации
y(x)= c1(x)y1(x) + c2(x)y2(x) + ... + cn(x)yn(x),
с неизвестными функциями c1(x), c2(x), ..., cn(x);
составить и решить систему для c1 (x), c2(x), ..., cn(x);
подставить вычисленные ci(x) = Fi(x) + Ci в выражение для решения и записать для него начальные условия;
найти из начальных условий значения констант Ci и записать искомое решение.
Для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует
найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения l1, l2, ... , ln, записать фундаментальную систему решений y1(x), y2(x), ..., yn(x));
найти методом вариации произвольных постоянных любое частное решение неоднородного уравнения yч(x);
записать выражение для общего решения
y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x).
12. Автономные системы на плоскости. Фазовая плоскость. Векторное поле
Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
В теории автономных систем принято обозначать независимую переменную буквой t, а искомое решение — ![]() .
.
Ограничимся случаем n = 2 и в дальнейшем рассматриваем автономные системы второго порядка:
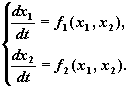
Будем полагать, что правые части системы f1(x1, x2 ) , f2(x1, x2) непрерывно дифференцируемы в области ![]() , т.е. справедлива теорема существования и единственности. Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1/dt и dx2/dtзависят только от x1 и x2. Автономные системы называют также динамическими системами.
, т.е. справедлива теорема существования и единственности. Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1/dt и dx2/dtзависят только от x1 и x2. Автономные системы называют также динамическими системами.
Пусть x1=j1(t), x2= j2(t) — решение автономной системы второго порядка. Тогда уравнения
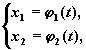
задают в параметрической форме кривую на плоскости. Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Для n >2 фазовые траектории располагаются в фазовом пространстве.
Если на рисунке изображено несколько фазовых кривых системы, характеризующих качественное поведение решений системы (кривые с одинаковыми асимптотами, предельными точками и пр.), то такое изображение называется фазовым портретом системы.
Интегральные кривые рассматриваемой системы изображаются в трехмерном пространстве переменных (t, x1, x2) и, если x1=f1(t), x2= f2(t) — решение системы, то интегральная кривая задается в параметрической форме уравнениями
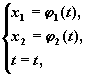
а фазовая траектория — не что иное, как проекция интегральной кривой на фазовую плоскость (плоскость (x1, x2).
Для фазовых кривых (фазовых траекторий) автономной системы с непрерывно дифференцируемой правой частью
![]() ,
, ![]() ,
,
справедливы следующие утверждения:
-
Если существует такая точка
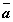 , что
, что 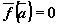 , то
, то  , является решением автономной системы, т.е. соответствующая фазовая траектория — точка.
, является решением автономной системы, т.е. соответствующая фазовая траектория — точка. -
Если точка (x1(t), x2(t)) принадлежит некоторой фазовой кривой, то при любой постоянной С точка (x1(t+С), x2(t+С)) принадлежит той же фазовой кривой.
-
Две фазовые кривые либо не имеют общих точек, либо совпадают.
-
Фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор).
-
Всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
-
Если фазовая кривая, отвечающая решению
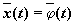 , есть гладкая замкнутая кривая, то это решение — периодическая функция.
, есть гладкая замкнутая кривая, то это решение — периодическая функция.
Точка ![]() , в которой правая часть системы обращается в нуль,
, в которой правая часть системы обращается в нуль,![]() , называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.
, называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.
Если в каждой точке области задан n-мерный вектор
,
, то говорят, что в области G задано векторное поле. Запишем автономную систему второго порядка
в векторной форме:
где
,
Автономная система
полностью определяется заданием векторного поля
.
Действительно, в каждой точке
гладкой фазовой кривой
существует касательный вектор
(x'(t0 ), y'(t0 ))
равный (в силу системы) вектору
,
иными словами, векторное поле
автономной системы задает в каждой точке направление касательной к фазовой кривой системы, проходящей через эту точку.
Точки векторного поля, в которых вектор — нулевой, называют особыми точками векторного поля. Таким образом, точки покоя автономной системы — это особые точки векторного поля.
13. Точки покоя автономной линейной системы
Рассмотрим автономную систему второго порядка:
Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1 /dt и dx2 /dt зависят только от x1 и x2 и не зависят от t.
Обозначим
и
.
Пусть — решение автономной системы второго порядка. Тогда уравнения
задают в параметрической форме кривую на плоскости . Эта кривая называется фазовой кривойили фазовой траекторией системы.Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы.
Точка , в которой правая часть системы обращается в нуль,
, называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.
Точка покоя называется устойчивой по Ляпунову, если:
1) существует такое , что для
при
существует решение задачи Коши с начальным условиям
;
2) для всякого существует такое
, что если
и
, то
при всех
.
Устойчивая точка покоя называется асимптотически устойчивой, если
при достаточно малых
.
Очевидно, что линейная автономная система
имеет единственную точку покоя: x1(t) = 0, x2(t) = 0, при всех . При этом характер точки покоя (0, 0) (ее устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по значениям собственных чисел l1 и l2 матрицы системы.
А именно, пусть l1 и l2 — собственные значения матрицы A исследуемой системы:
-
если l1 и l2— действительные отрицательные числа, то точка покоя устойчива и называется устойчивым узлом;
-
если l1 и l2 — действительные положительные числа, то точка покоя неустойчива и называется неустойчивым узлом;
-
если l1 и l2 — действительные числа, имеющие разные знаки, то точка покоя неустойчива и называется седлом;
-
если l1 и l2 — комплексные числа, l1,2 =Rell ± Imll и Rel не превышает нуля, то точка покоя устойчива, точнее, при Rel =0 точка устойчива, но не асимптотически устойчива и называется центром, при Rel< 0 она асимптотически устойчива и называется устойчивым фокусом, а если Rel>0, то точка покоя неустойчива и называется неустойчивым фокусом;
-
если l1 = l2 - отличные от нуля действительные числа, то точка покоя — узел специального вида, называемый диакритическим, устойчивым при отрицательных l1 = l2 и неустойчивым при положительных l1 = l2;
-
если l1 = 0 и l2 № 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя;
-
если l1 = l2 = 0, то все точки плоскости являются точками покоя.
14. Автономные системы на плоскости. Предельные циклы
Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
Рассмотрим автономные системы второго порядка:
Будем полагать, что правые части системы f1(x1, x2), f2(x1, x2) непрерывно дифференцируемы в области определения, т.е. справедлива теорема существования и единственности.
Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1/dt и dx2/dt зависят только от x1 и x2. Автономные системы называют также динамическими системами.
Пусть x1=j1(t), x2=j2(t) — решение автономной системы второго порядка. Тогда уравнения
задают в параметрической форме кривую на плоскости (x1, x2). Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Именно поэтому автономные системы второго порядка принято называть автономными системами на плоскости.
Для фазовых траекторий автономной системы с непрерывно дифференцируемой правой частью справедливы следующие утверждения:
-
две фазовые кривые либо не имеют общих точек, либо совпадают;
-
фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор);
-
всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
Если фазовая траектория x1=j1(t), x2=j2(t) — замкнутая гладкая кривая g, в некоторой окрестности которой нет других замкнутых траекторий, то она является предельным циклом: все траектории, которые начинаются достаточно близко от g, спиралевидно приближаются к ней либо при , либо при
.
Предельные циклы бывают трех типов:
-
устойчивые — близкие траектории "навиваются" на него при
;
-
неустойчивые — близкие траектории уходят от него при
;
-
полуустойчивые — траектории, лежащие по одну сторону от цикла, "навиваются" на него при
, а лежащие по другую строну — "отходят" от цикла.
15. Жесткие системы дифференциальных уравнений
В вычислительной практике часто встречаются системы дифференциальных уравнений, которые принято называть жесткими.
Не приводя точного определения жесткой системы, проиллюстрируем содержание этого понятия и возникающие проблемы на примере жесткой линейной системы двух дифференциальных уравнений с постоянными коэффициентами.
Пусть требуется численно решить задачу Коши
y'1 = -2y1 - 998 y2 ,
y'2 = - 1000y2 ,
y1 (0) = 2, y2 (0)=1.
Эту задачу можно записать в матричной форме в виде:
![]()
где
![]()
искомое решение,
![]()
матрица системы,
![]()
значение решения в начальной точке x = 0 — начальное условие.
Легко видеть, что точное решение системы имеет вид:
y1 (x) = exp(-2x) + exp(-1000x),
y2 (x) = exp(-1000x).
Слагаемое
exp(-1000x)
убывает очень быстро,
а слагаемое exp(-2x) — гораздо медленнее.
Попытаемся найти решение этой задачи методом Рунге-Кутты с различными шагами. Графики полученных решений и графики точного решения приведены ниже (график точного решения - справа).
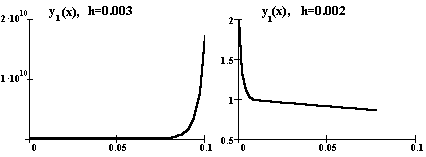

Видно, что полученные приближенные решения уже на первых шагах содержат большие ошибки. Для получения правдоподобного результата на отрезке [0, 0.1] нужно выбирать шаг, меньший 0.003. Это означает, что для достаточно большого интервала интегрирования потребуется выполнить вычисления для очень большого числа шагов. Казалось бы, можно избежать интегрирования на всем промежутке с малым шагом: вести вычисления с малым шагом до тех пор, пока компонента
exp(-1000x)
станет пренебрежимо малой, а затем увеличить шаг и до конца промежутка интегрирования вести вычисления с большим шагом. Оказывается, что на самом деле это совсем не так. Вторая компонента заставляет вести интегрирование с малым шагом на всем промежутке интегрирования. Это и означает, что система жесткая. Жесткость системы проявляется тогда, когда длина промежутка интегрирования T удовлетворяет соотношению ![]()
где lmax — наибольшее по абсолютной величине собственное число матрицы системы A. Для интегрирования жестких систем необходимо применять специально разработанные методы.
В примере рассмотрена линейная жесткая система. Однако специальные методы решения жестких систем, как правило, универсальны, т.е. применяются для решения как линейных так и нелинейных систем.
16. Решение задачи Коши операционным методом
Операционное исчисление — один из наиболее экономичных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. При решении операционным методом задача интегрирования линейного дифференциального уравнения с постоянными коэффициентамисводится к задаче о решении алгебраического уравнения.
Функцией-оригиналом называется функция f(x) для которой справедливо:
f(x) непрерывна при неотрицательных x, за исключением, быть может конечного числа точек,
f(x)=0 при x<0,
существуют такие постоянные M и a, что
![]()
при всех неотрицательных x.
Преобразованием Лапласа функции f(x) называется функция
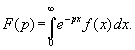
Функция F(p) называется изображением функции f(x), а функция f(x) - оригиналом для F(p).
Основные свойства преобразования Лаплалса, используемые при решении дифференциальных уравнений следующие:
-
оригинал восстанавливется по изображению единственным образом, с точностью до значений в точках разрыва - теорема единственности;
-
если F(p) и G(p) - изображения соответственно для f(x) и g(x), то изображением для
af(x)+bg(x)
является aF(p) +bG(p) - линейность преобразования Лапласа; -
изображением для производной f (n)(x) является функция
pnF(p)-pn-1f(0)-pn-2f'(0)- …- pf (n-2)(0)-f (n-1)(0) - изображение производных; -
если F(p) изображения для f(x), то для любого a>0 изображением для f(x-a) является
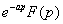 - теорема запаздывания.
- теорема запаздывания.
Рассмотри задачу Коши:
![]()
a1, a2, …, an - постоянные.
Алгоритм решения задачи Коши для уравнений операционным методом состоит в следующем. Обозначим Y(p) и F(p) изображения для y(x) и f(x).
Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим: ![]()
или, A(p)Y(p)+B(p) = F(p), где A(p) и B(p) - многочлены.
Отсюда:
![]()
и искомое решение задачи Коши y(x) является оригиналом для Y(p).
Совершенно аналогично операционное исчисление применяется к решению задачи Коши для системлинейных дифференциальных уравнений с постоянными коэффициентами. Рассмотрим задачу Коши:
![]()
A- постоянна матрица размерности n·n.
Алгоритм решения задачи Коши для систем операционным методом состоит в следующем.
Обозначим ![]() изображения для
изображения для ![]() - компонентами вектор-функций
- компонентами вектор-функций ![]() являются изображения соответствующих компонент вектор-функций
являются изображения соответствующих компонент вектор-функций ![]() . Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
. Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
![]()
![]() ,
,
где E - единичная матрица, ![]() - обратная матрица к матрице
- обратная матрица к матрице ![]() .
.
Тогда искомое решение задачи Коши ![]() является оригиналом для
является оригиналом для ![]() .
.
Наверх
17. Приложения обыкновенных дифференциальных уравнений к задачам биологии и экономики
Дифференциальные уравнения широко используются для моделирования реальных систем, зависящих от времени, в частности, для описания и исследования экономических и биологических систем.
Динамика популяций. Уравнения Вольтерра-Лотка
В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка. Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества.
Пусть x1 и x2 — число жертв и хищников соответственно. Предположим, что относительный прирост жертв x1'/x1 равен a-bx2, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, -bx2 — потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x1=0 ) относительная скорость изменения популяции хищников равна ![]() , c>0 , наличие пищи компенсирует убывание, и при x1>0 имеем
, c>0 , наличие пищи компенсирует убывание, и при x1>0 имеем ![]() , d>0.
, d>0.
Таким образом, система Вольтерра—Лотка имеет вид:
.gif)
где a, b, c, d >0.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и пр.
Рассмотрим фазовый портрет системы Вольтерра—Лотка для a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x1(0)=3, x2(0)=1, построенные программой ОДУ.
.gif)
.gif)
Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3 : 1 , обе популяции сначала растут. Когда число хищников достигает величины b=2.5 , популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x1=c/d =2 (в этой точке x2'=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины x2=a/b =1.6 (в этой точке x1'=0).С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и ... процесс повторяется снова и снова. На графике четко виден периодический характер процесса. Количество жертв и хищников колеблется возле величин x1=2, x2=1.6 соответственно (дробные числа здесь не означают “половину волка”, величины могут измеряться в сотнях, тысячах и т.п.). Периодичность процесса явственно видна на фазовой плоскости — фазовая кривая (x1(t), x2(t)) — замкнутая линия. Самая левая точка, этой кривой, - это точка, в которой число жертв достигает наименьшего значения. Самая правая точка x1=4,x2=1.6 , — точка пика популяции жертв. Между этими точками количество хищников сначала убывает, до нижней точки фазовой кривой,x1=2 , где достигает наименьшего значения, а затем растет до верхней точки фазовой кривой (x1=2, x2=2.5). Фазовая кривая охватывает точку x1=2, x2=1.6.
На языке дифференциальных уравнений это означает, что система имеет стационарное состояние
x1' =0, x2' =0,
которое достигается в точке x1=2, x2=1.6. Если в начальный момент система находилась в стационарной точке, то решения x1(t), x2(t) не будут изменяться во времени, останутся постоянными. Всякое же другое начальное состояние приводит к периодическому колебанию решений. Неэллиптичность формы траектории, охватывающей центр, отражает негармонический характер колебаний.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.
Уравнения Вольтерра-Лотка с логистической поправкой
Рассмотрим модель конкурирующих видов с “логистической поправкой”:
.gif)
В этом случае поведение решений в окрестности стационарной точки меняется в зависимости от величины и знака параметра a.
Рассмотрим фазовый портрет системы Вольтерра—Лотка для a =0.1, a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x1(0)=3, x2(0)=1, построенные программой ОДУ.
.gif)
.gif)
Видно, что в этом случае стационарная точка превращается в устойчивый фокус, а решения — в затухающие колебания. При любом начальном условии состояние системы через некоторое время становится близким к стационарному и стремится к нему при ![]() .
.
Графики решений и фазовая кривая при отрицательном значении параметра a, a =-0.1, приведены ниже.
.gif)
.gif)
Как видно, в этом случае стационарная точка является неустойчивым фокусом и амплитуда колебаний численности видов растет. В этом случае как бы близко ни было начальное состояние к стационарному, с течением времени состояние системы будет сильно отличаться от стационарного.
Модель Холлинга-Тэннера
На примере модели Вольтерра—Лотка и модели Вольтерра—Лотка с логистической поправкой было продемонстрировано одно из важнейших качественных свойств центров — они легко разрушаются даже при самых малых изменениях правой части. Большинство моделей является идеализацией действительности; в них внимание сосредоточено на некоторых основных переменных и соотношениях между ними. Поэтому устойчивость моделей относительно малых возмущений чрезвычайно важна в приложениях. Модели, не чувствительные к малым возмущениям, называются грубыми.
Модель Вольтерра—Лотка неустойчива относительно возмущений, поскольку ее стационарное состояние — центр.
Существует другой вид моделей, в которых возникают незатухающие колебания, — это модели, имеющие на фазовых портретах предельные циклы. Такая модель существует для системы конкурирующих видов — это модель Холлинга—Тэннера.
Скорость роста популяции жертв x'1 в этой модели равна сумме трех величин:
-
скорости размножения в отсутствие хищников — r x1;
-
влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей это влияние ограниченных сырьевых ресурсов) —
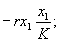
-
влиянию хищников , в предположении, что хищник перестает убивать, когда насыщается —
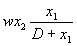
Скорость роста популяции хищников x'2 строится так же, как в модели Вольтерра—Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно J жертв, то популяция из x1 жертв сможет обеспечить пищей x1/J хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид
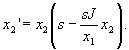 .
.
Таким образом, имеем модель Холлинга—Тэннера:
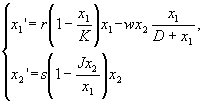
где r, s, K, D, J > 0.
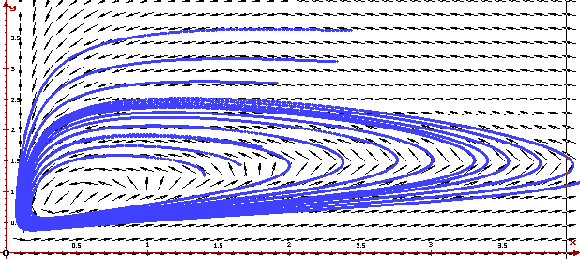
Можно показать, что при
![]()
на фазовом портрете системы будет устойчивый предельный цикл. Ниже приведено решение системы при r=1, K=7, w=1, D=1, s=0.2, J=0.5 и двух различных начальных состояниях и фазовый портрет системы, построенные программой ОДУ.


Выравнивание цен
Модель выравнивания цен по уровню актива интересна тем, что в ней можно наблюдать гармонические колебания решений возле стационарного состояния. Предположим, что изменение уровня актива q пропорционально разности между предложением s и спросом d, т.е. q'=k(s-d), k > 0. Предположим далее, что изменение цены p пропорционально отклонению актива q от некоторого фиксированного уровня q0 так, что p'=-m(q-q0 ) , m > 0. Таким образом, модель выравнивания цен по уровню актива имеет вид
q' = k(s(p) - d(p)),
p' = - m(q-q0).
Ниже приведены график решения и фазовая кривая для
s(p)=ap+s0 ,
d(p)=cp+d0 ,
k=0.3, m=0.1,
q0 =20, a=20,
s0 =10, d0 =50, c=-10
при начальном состоянии
q(0)=19, p(0)=2,
построенной программой ОДУ.
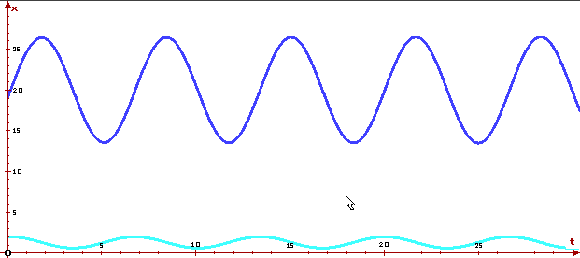
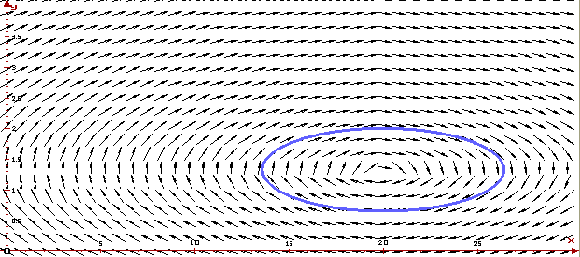
Видно, что цена и актив колеблются возле стационарного состояния. Фазовая траектория представляет собой эллипс, охватывающий стационарную точку. Это означает, что колебания актива и цены — гармонические.
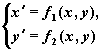
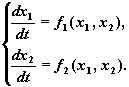

.GIF)
.GIF)
Комментарии
nice