Курс по теории функций комплексного переменного
Небольшой теоретический курс по теории функций комплексного переменного.
1. Различные формы представления комплексных чисел. Арифметические операции с комплексными числами.
2. Элементарные функции комплексного переменного.
3. Дифференцирование функций комплексного переменного.
4. Интегралы в комплексной области.
5. Нули аналитической функции.
6. Изолированные особые точки функции комплексного переменного.
7. Ряд Тейлора функций комплексного переменного.
10. Вычисление интегралов по замкнутому контуру.
11. Вычисление несобственных интегралов.
12. Преобразование Лапласа. Решение задачи Коши операционным методом.
Различные формы представления комплексных чисел. Арифметические операции с комплексными числами
Комплексным числом z называется упорядоченная пара действительных чисел x и y.
Первое из них x называется действительной частью комплексного числа z и обозначается Rez, x = Rez;
второе число y называется мнимой частью комплексного числа z и обозначается Imz, y = Imz.
Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:
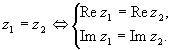
Алгебраическая форма записи комплексного числа
![]()
Число
![]()
![]() , где
, где ![]()
называется комплексно сопряженным числу
![]()
![]()
Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).
Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью
x = rcosj, y = rsinj
получим тригонометрическую форму записи комплексного числа:
z = r (cosj + isinj) .
При этом число r называют модулем комплексного числа, |z| = r, а число j - аргументом комплексного числа,
Arg z = arg z+2kp= j.
При решении задач для вычисления аргумента удобно пользовааться схемой, приведенной ниже:
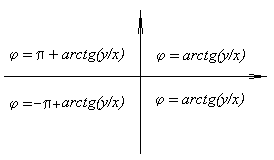
Справедливы соотношения:
![]()
Используя формулу Эйлера
![]()
получим показательную форму записи комплексного числа:
![]()
Арифметические операции c комплексными числами определяются следующим образом:
если
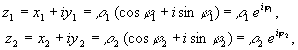
то
![]()
![]()
Элементарные функции комплексного переменного
Значение целой положительной степени комплексного аргумента, значение функции f(z) = z n , проще всего вычислять в тригонометрической форме.
Если z = x + iy = r (cosj + isinj ), то для любого целого положительного числа n имеет место формула:
w = f(z) = z n = r n (cos nj + isin nj ).
Если w = f (z) = f (x + iy) = u(x, y) + iv(x, y), то
u(x, y) = r ncos nj , u(x, y) = r nsin nj.
Корнем n-й степени из комплексного числа z называется число
![]() такое, что wn = z.
такое, что wn = z.
Для любого комплексного числа z существует n комплексных чисел w таких, что wn = z.
Значение корня, т.е. значение функции
![]()
проще всего вычислять в тригнометрической форме.
Если z = x + iy = r (cosj + isinj), то для любого целого положительного числа n имеет место формула:
![]()
Т.е. функция
![]()
является многозначной функцией _ каждому значению аргумента отвечает n различных значений корня.
Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то ![]()
Если z = x + iy = r (cosj + isinj ), то значения функции f(z) = exp(z) вычисляются по формуле
f(z) = ez = ex+iy = e xe iy = ex (cosy + isiny).
Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то
u(x,y) = ex cosy , v(x,y) = ex siny.
Тригонометрические функции комплексного аргумента определяются формулами:
![]()
Гиперболические функции комплексного переменного определяются совершенно так же, как функции в действительной области:
![]()
Логарифмом комплексного числа z называется такое число w, что
exp(w) = z.
Значения логарифмической функции f(z) = Ln(z) вычисляются по формуле
Ln(z) = ln(|z|) + iArg z = ln(|z|) + iarg z + 2kp i, k = 0,1,2,...
Величину ln(|z|) + iarg z называют главным значением логарифма.
Функция f(z) = Ln(z) является многозначной функцией _ каждому значению аргумента отвечает бесконечное множестворазличных значений логарифма.
Показательная (f(z) = az) и степенная (f(z) = za) функции комплексного переменного определяются с помощью логарифма - для любых комплексных чисел a и z справедливо:
f(z) = az = ezLna;
f(z) = za= eaLnz.
Значения обратных тригонометрических функций комплексного переменного вычисляются по формулам:
 .
.
Дифференцирование функций комплексного переменного
Производная функции комплексного переменного определяется, как и производная в действительной области:
![]()
Здесь
z0, Dz _ комплексные и Df(z0) = f(z0+Dz) - f(z).
Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.
1. Сумма и произведение дифференцируемых в точке функций, есть функция и справедливы равенства:
![]()
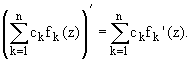
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :
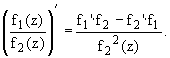
3. Сложная функция f(j (z)) дифференцируема в точке z0, если в этой точке дифференцируема функция j (z), а функция f(u) дифференцируема в точке u0,
где u0 = j (z0) и u = j (z). При этом в точке z0 имеет место формула:
![]()
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.
Например, рассмотрим функцию f(z) = z3.
По определению производной для любой точки z, принадлежащей комплексной области, записываем:
![]()
Предел существует для любой точки z, принадлежащей комплексной области и
(z3)' =3z2.
Аналогично можно получить:
(zn)' = nzn-1 (n - действительное число).
Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z),
то справедливы следующие утверждения:
1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей
u(x, y) = Re f(z), v(x, y) = Im f(z)
и выполняется условие Коши-Римана:
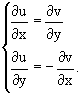
2. Если u(x, y) и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция f(z) = f(x+iy) = u(x, y) + iv(x, y) дифференцируема в точке z0 = x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из формул:
![]()
![]()
![]()
![]()
Интегралы в комплексной области.
Интегралом от функции комплексного переменного называется предел последовательности интегральных сумм; функция при этом определена на некоторой кривой l, кривая предполагается гладкой или кусочно-гладкой:
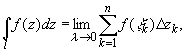
где ![]() - точка, произвольно выбранная на дуге
- точка, произвольно выбранная на дуге ![]() разбиения кривой,
разбиения кривой,
![]() - приращение аргумента функции на этом участке разбиения,
- приращение аргумента функции на этом участке разбиения,
![]() - шаг разбиения,
- шаг разбиения,
![]() - длина хорды, соединяющей концы дуги
- длина хорды, соединяющей концы дуги ![]() ,
,
кривая l разбивается произвольным образом на n частей ![]() , k=1,2...n.
, k=1,2...n.
На кривой выбрано направление, т.е. указаны начальная и конечная точки.
В случае замкнутой кривой l = C
![]()
интегрирование происходит в положительном направлении, т.е. в направлении обхода, оставляющем слева конечную область, ограниченную контуром С.
Существует несколько способов вычисления интегралов в комплексной области.
1 способ. Интеграл вычисляется сведением к криволинейным интегралам от функций действительных переменных - примененяются формулы:
![]()
где f(z) = u + iv, u = Re f(z), v = Im f(z).
2 способ. Интеграл вычисляется сведением к определенному интегралу (путь интегрирования l задается в параметрической форме z = z(t)) - применяется формула:
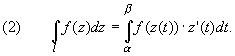
3 способ. Вычисление интегралов от аналитической функции в односвязных областях - примененяеется формула:
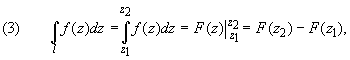
где F(z) - первообразная для f(z).
Нули аналитической функции.
Пусть функция f (z) является аналитической в точке z0. Точка z0 называется нулем функции f (z), если ее значение в этой точке равно нулю, т.е. f (z0) = 0.
В разложении функции в ряд Тейлора в окрестности нуля этой функции (т. z0) отсутствует свободный член: С0 = f(z0) = 0.
Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности (z-z0) до n-ой степени, т.е. разложение имеет вид: ![]()
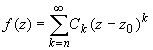 или
или ![]() то точка z0 называется нулем порядка nфункции f(z).
то точка z0 называется нулем порядка nфункции f(z).
Нуль первого порядка (n = 1) называется простым нулем.
Следующие условия являются необходимым и достаточным условиями нуля порядка n функции f (z) в точке z0:
a). ![]()
b). представление функции в виде произведения:![]()
Порядок нуля в точке z0 функции, полученной в результате перемножения аналитических функций
f (z) = f1(z) f2(z) равен сумме порядков нуля (n1 + n2) в этой точке функций сомножителей
( n1 - порядок нуля в точке z0 функции f1(z), n2 - порядок нуля в точке z0 функции f2(z) ).
Изолированные особые точки функции комплексного переменного.
Точка z0, принадлежащая области комплексных чисел, называется изолированной особой точкой функции f(z), если ![]() такая, что f(z) является однозначной аналитической функцией в
такая, что f(z) является однозначной аналитической функцией в ![]() (в самой точке аналитичность f(z) нарушается).
(в самой точке аналитичность f(z) нарушается).
Изолированная особая точка z0 функции f(z) называется:
-
устранимой особой точкой, если
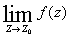 существует и конечен;
существует и конечен; -
полюсом, если
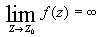 ;
; -
существенно особой точкой, если
.gif) не существует.
не существует.
Для того чтобы особая точка функции f(z) была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если z0 - устранимая особая точка, то ряд Лорана функции f(z) имеет вид:  (1)
(1)
для z0 - конечной точки, принадлежащей области комплексных чисел.
Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов.
Ряд Лорана функции f(z) в случае z0-полюс имеет вид:
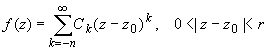 (2)
(2)
если z0 принадлежит области комплексных чисел.
Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка z0 является полюсом порядка n функции f(z), если в разложении (2) ![]() , Ck = 0 при k < -n.
, Ck = 0 при k < -n.
Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции f(z) в случае z0 - существенно особой точки имеет вид:  (3)
(3)
если z0 принадлежит области комплексных чисел.
Ряд Тейлора функций комплексного переменного.
Теорема Тейлора (о разложении функции в степенной ряд).
Функция, аналитическая в области комплексных чисел D, в окрестности каждой точки z0 этой области представляется в виде степенного ряда:
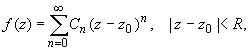 (1)
(1)
радиус сходимости R которого не меньше, чем расстояние от точки z0 до границы области D.
Такой степенной ряд называется рядом Тейлора.
Коэффициенты ряда Тейлора вычисляются по формуле:
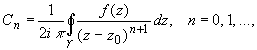 (2)
(2)
где ![]() - произвольный контур, принадлежащий области D и охватывающий точку z0 (в частности,
- произвольный контур, принадлежащий области D и охватывающий точку z0 (в частности, ![]() - окружность
- окружность ![]() ), или по формуле:
), или по формуле:
![]() (3)
(3)
Радиус сходимости ряда Тейлора равен расстоянию от точки z0 до ближайшей особой точки функции.
Для вычисления радиуса сходимости ряда Тейлора можно также использовать формулы:
![]()
![]()
Основные разложения.
![]() (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
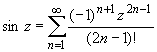 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
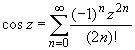 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
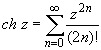 (z принадлежит области комплексных чисел);
(z принадлежит области комплексных чисел);
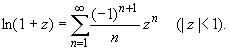
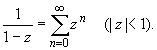
Ряды Лорана.
Теорема Лорана (о разложении функции в ряд по целым степеням).
Функция f(z), аналитическая в кольце
r < | z - z0 | < R, ![]()
представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство:
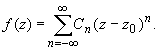 (1)
(1)
Коэффициенты ряда вычисляются по формуле: 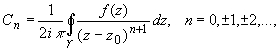 (2)
(2)
где ![]() - произвольный контур, принадлежащий кольцу и охватывающий точку z0; в частности,
- произвольный контур, принадлежащий кольцу и охватывающий точку z0; в частности,
![]() - окружность
- окружность ![]()
Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f(z).
Совокупность членов ряда с неотрицательными степенями 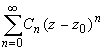 называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:
называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:
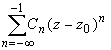 или
или 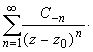
Для коэффициентов ряда имеет место формула оценки коэффициентов - неравенство Коши:
![]() где
где ![]()
r - радиус контура интегрирования в формуле (2).
На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f(z) - его суммы.
Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z0 (r = 0) и в окрестности бесконечно удаленной точки (z0 = 0, ![]() ).
).
При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами.
Вычеты.
Вычетом функции f(z) в изолированной особой точке z0 (точка принадлежит области комплексных чисел) называется интеграл вида:
.gif)
где ![]() - контур, принадлежащий окрестности точки z0 и охватывающий ее. Обход контура - положительный, т.е. область ограниченная им и принадлежащая окрестности z0 при обходе расположена слева: обход против часовой стрелки.
- контур, принадлежащий окрестности точки z0 и охватывающий ее. Обход контура - положительный, т.е. область ограниченная им и принадлежащая окрестности z0 при обходе расположена слева: обход против часовой стрелки.
Обозначается вычет .gif)
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z-z0) для z0, принадлежащей области комплексных чисел: ![]()
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то ![]()
Если z0 - полюс порядка n функции f(z), z0 принадлежит области комплексных чисел, то
![]()
![]()
Если z0 - простой полюс функции ![]() ,
,
где ![]() аналитические функции в точке z0 и
аналитические функции в точке z0 и ![]() ,
,
то ![]()
Вычисление интегралов по замкнутому контуру.
Теорема (Основная теорема о вычетах).
Если функция f(z - аналитична в ![]() за исключением конечного числа особых точек
за исключением конечного числа особых точек ![]() , то справедливо равенство
, то справедливо равенство
![]()
где D - односвязная область в комплексной плоскости, ![]() - граница D,
- граница D,
![]() - вычет функции f(z) в точке zk.
- вычет функции f(z) в точке zk.
Вычисление несобственных интегралов
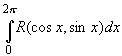 ~
~  ~
~ 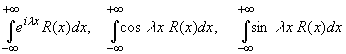
Утверждение. Пусть R(x, y) - рациональная функция двух действительных переменных. Тогда справедливы равенства 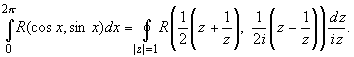
Действительно, замена z = eix переводит отрезок ![]() в окружность |z| = 1,
в окружность |z| = 1,
![]() .
.
При этом: ![]()
В результате имеем формулу, сопоставляющую интеграл от действительной переменной с интегралом по замкнутой кривой от функции комплексного переменного:
.gif)
Замечание. Для вычисления таких интегралов в математическом анализе в общем случае, за исключением некоторых частных случаев, применяется замена tg(1/2)= t ("универсальная" подстановка) и интеграл приводится к интегралу от рациональной дроби.
Утверждение. Пусть функция ![]()
где Pn(x) и Qm(x) - многочлены степени n и m (n = const, m = const), удовлетворяет условиям:
1. (m - n) больше или равно 2.
2. Qm(x) не равна 0 при x, принадлежащим области действительных чисел.
Тогда справедливы равенства:

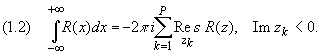
Здесь zk, k = 1,2,..., p - все особые точки функции R(z), расположенные выше оси Ох (Im zk> 0) в случае формулы (1) и ниже оси Ох (Im zk< 0) в случае формулы (1.2).
Замечание. Если R(z) - четная функция, то можно, используя формулы (1.1) и (1.2), вычислить интеграл вида 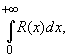
т.к. для четной функции имеет место равенство: 
Утверждение. Пусть R(x) - рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, - нуль порядка не ниже первого (т.е. (m - n) больше или равно 1). Тогда справедливы формулы:
![]()
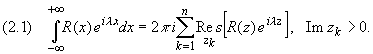
![]()
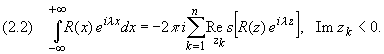
![]()
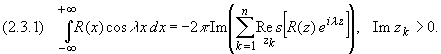
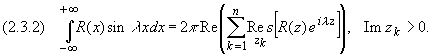
Преобразование Лапласа. Решение задачи Коши операционным методом
Операционное исчисление - один из наиболее эффективных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. При решении операционным методом задача интегрирования линейного дифференциального уравнения с постоянными коэффициентами сводится к задаче о решении алгебраического уравнения.
Функцией-оригиналом называется функция f (x) для которой справедливо:
f (x) непрерывна при неотрицательных x, за исключением, быть может конечного числа точек, f (x) = 0 при x<0, существуют такие постоянные M и a, что ![]() при всех неотрицательных x.
при всех неотрицательных x.
Преобразованием Лапласа функции f (x) называется функция 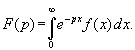
Функция F (p) называется изображением функции f (x), а функция f (x) - оригиналом для F (p).
Основные свойства преобразования Лапласа, используемые при решении дифференциальных уравнений следующие:
-
оригинал восстанавливется по изображению единственным образом, с точностью до значений в точках разрыва - теорема единственности;
-
если F (p) и G (p) - изображения соответственно для f (x) и g (x), то изображением для af (x) + bg (x) является aF (p) + bG (p) - линейность преобразования Лапласа;
-
изображением для производной f (n)(x) является функция pnF(p) - pn-1f (0) - pn-2f '(0) -...- pf (n-2)(0) - f (n-1)(0) - изображение производных;
-
если F (p) изображения для f (x), то для любого a>0 изображением для f (x-a) является
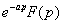 - теорема запаздывания.
- теорема запаздывания.
Рассмотри задачу Коши:
![]()
a1, a2, ..., an - постоянные.
Алгоритм решения задачи Коши для уравнений операционным методом состоит в следующем. Обрзначим Y (p) и F (p) изображения для y (x) и f (x).
Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим: ![]()
или, A (p)Y (p) + B (p) = F (p), где A (p) и B (p) - многочлены.
Отсюда:
![]()
и искомое решение задачи Коши y (x) является оригиналом для Y (p).
Совершенно аналогично операционное исчисление применяется к решению задачи Коши для систем линейных дифференциальных уравнений с постоянными коэффициентами. Рассмотри задачу Коши:
![]()
A- постоянна матрица размерности n.n.
Алгоритм решения задачи Коши для систем операционным методом состоит в следующем.
Обозначим ![]() изображения для
изображения для ![]() - компонентами вектор-функций
- компонентами вектор-функций ![]() являются изображения соответствующих компонент вектор-функций
являются изображения соответствующих компонент вектор-функций ![]() . Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
. Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
![]()
![]() ,
,
где E - единичная матрица, ![]() - обратная матрица к матрице
- обратная матрица к матрице![]() . Тогда искомое решение задачи Коши
. Тогда искомое решение задачи Коши ![]() является оригиналом для
является оригиналом для ![]() .
.
Комментарии