Курс "Введение в вычислительную математику"

Данный курс посвящен введению в вычислительную математику.

1. Теория погрешностей и машинная арифметика.

2. Решение нелинейных уравнений. Методы бисекций, простой итерации, Ньютона.

3. Решение нелинейных уравнений. Обусловленность задачи нахождения корня. Интервал неопределенности.

4. Решение систем линейных алгебраических уравнений. Нормы векторов и матриц. LU-разложение матрицы.

5. Решение систем линейных алгебраических уравнений прямыми методами.

6. Решение систем линейных алгебраических уравнений итерационными методами.

7. Приближение функций. Метод наименьших квадратов.

8. Приближение функций. Интерполяция.

9. Приближение функций. Сплайны.

10. Решение задачи Коши одношаговыми методами. 

Наверх

1. Теория погрешностей и машинная арифметика.

Пусть  - точное значение, 

        - приближенное значение некоторой величины. 

Абсолютной погрешностью приближенного значения  называется величина  . 

Относительной погрешностью значения  (при  0) называется величина   . 

Так как, значение  как правило неизвестно, чаще получают оценки погрешностей вида:      . 

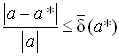Величины  и  называют верхними границами (или просто границами) абсолютной и относительной погрешностей. 

Значащими цифрами числа     называют все цифры в его записи, начиная с первой ненулевой слева.

Значащую цифру числа   называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре. 

Для оценки погрешностей арифметических операций следует использовать следующие утверждения:

Абсолютная погрешность алгебраической суммы (суммы или разности ) не превосходит суммы абсолютной погрешности слагаемых, т.е.

Если а и b - ненулевые числа одного знака, то справедливы неравенства

,       , 

где  ,    

Для относительных погрешностей произведения и частного приближенных чисел верны оценки: 

если  и  , то   , .

Пусть  - дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов    . Тогда для абсолютной погрешности функции  справедлива следующая оценка

 .

Здесь [x, x*] v отрезок, соединяющий точки x и x* =( ) 

Для относительной погрешности функции справедливо следующее приближенное равенство

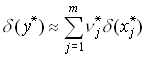 , где

Наверх

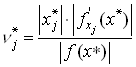
2. Решение нелинейных уравнений. Методы бисекций, простой итерации, Ньютона.

Пусть рассматривается уравнение . Корнем уравнения называется значение , при котором . Корень  называется простым, если 

, в противном случае корень называется кратным. Целое число m называется кратностью корня , если  для k=1,2,3-,m-1 и 

.

Постановка задачи вычисления приближенного значения корня с точностью : найти такое значения , что .

Решение задачи разбивается на два этапа: на первом этапе осуществляют локализацию корней, на втором этапе производят итерационное уточнение корней. На этапе локализации корней находят достаточно узкие отрезки ( или отрезок, если корень единственный), которые содержат один и только один корень уравнения . На втором этапе вычисляют приближенное значение корня с заданной точностью. Часто вместо отрезка локализации достаточно указать начальное приближение к корню.

Метод бисекции. Пусть [a,b] v отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков . 

Алгоритм метода бисекции состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Опишем один шаг итераций метода. Пусть на k-ом шаге найден отрезок  такой, что . Найдем середину отрезка . Если , то - корень и задача решена. Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:

, , если

, , если

Критерий окончания итерационного процесса: если длина отрезка локализации меньше 2, то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.

Теорема о сходимости метода бисекций. Пусть функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков .Тогда метод сходится и справедлива оценка погрешности :

Метод Ньютона (метод касательных) . Расчетная формула метода Ньютона имеет вид:

. Геометрически метод Ньютона означает, что следующее приближение к корню  есть точка пересечения с осью ОХ

касательной, проведенной к графику функции y=f(x) в точке . 

Теорема о сходимости метода Ньютона. Пусть  - простой корень уравнения , в некоторой окрестности которого функция дважды непрерывно дифференцируема. Тогда найдется такая малая - окрестность корня , что при произвольном выборе начального приближения  из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка 

, где , .

Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство .

Как указано в теореме, метод Ньютона обладает локальной сходимостью, то есть областью его сходимости является малая окрестность корня . Неудачный выбор может дать расходящуюся итерационную последовательность.

Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение  преобразовать к виду, удобному для итерации . Это преобразование можно выполнить различными способами. Функция  называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: .

Теорема о сходимости метода простой итерации. Пусть в некоторой - окрестности корня функция  дифференцируема и удовлетворяет неравенству , где  - постоянная . Тогда независимо от выбора начального приближения из указанной - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится

со скоростью геометрической последовательности и справедлива оценка погрешности:, .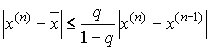

Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство 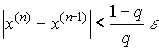. Если величина , то можно использовать более простой критерий окончания итераций: .

Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду . Предположим дополнительно, что производная  знакопостоянна и  на отрезке [a,b]. Тогда при выборе итерационного параметра  метод сходится и значение

 .

Наверх

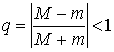3. Решение нелинейных уравнений. Обусловленность задачи нахождения корня. Интервал неопределенности.

Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям входных данных.

Пусть установлено неравенство , где  - относительная погрешность входных данных, а - относительная погрешность решения. Тогда - называется абсолютным числом обусловленности задачи. Если же установлено неравенство  между относительными погрешностями данных и решения, то  называют относительным числом обусловленности задачи. 

Обычно под числом обусловленности  понимают относительное число обусловленности. Если , то задачу называют плохо обусловленной.

Обусловленность задачи нахождения корня. Пусть  v корень, подлежащий определению. Будем считать, что входными данными для задачи вычисления корня являются значения функции . Так как v вычисляется приближенно, то обозначим функцию, полученную в действительности через . Предположим, что в малой окрестности корня выполняется неравенство: . Для близких к  значений  справедливо равенство , следовательно, . 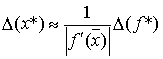Это означает, что число обусловленности задачи нахождения корня равно . Из последней формулы следует, что чем меньше значение производной функции в точке корня, тем задача хуже обусловлена. В частности, задача нахождения кратного корня имеет число обусловленности - бесконечность. 

Интервал неопределенности корня. Если функция  непрерывна, то найдется такая малая окрестность   корня , имеющая радиус , в которой выполнено неравенство . Это означает, что  знак вычисленного значения  , вообще говоря не обязан совпадать со знаком  и, следовательно, становится невозможным определить, какое именно значение  из интервала  обращает функцию  в нуль. Этот интервал называется интервалом неопределенности корня. Очевидно, что радиус интервала неопределенности для простого корня равен 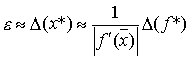. Аналогично можно показать, что для кратного корня . Это означает, что для простого корня радиус интервала неопределенности прямо пропорционален погрешности вычисления функции , а для кратного корня .

Пусть . Корень уравнения простой и равен  = -0.34729635533861. Тогда  и . Если , то . Это означает , что найти корень с точностью меньшей, чем радиус интервала неопределенности, не удастся. 

Применение метода Ньютона для нахождения кратного корня. Метод Ньютона для случая кратного корня обладает лишь линейной скоростью сходимости. Чтобы сохранить квадратичную сходимость его модифицируют следующим образом:

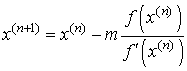, где  - кратность корня. 

Как правило, значение  v неизвестно. Используя метод Ньютона, можно узнать кратность корня. Для этого будем задавать значения = 1,2,3 и вычислять значение корня с заданной точностью , одновременно подсчитывая количество итераций для каждого значения . При некотором значении число итераций будет минимальным. Это значение  и есть кратность корня.

Наверх

4. Решение систем линейных алгебраических уравнений. Нормы векторов и матриц. LU-разложение матрицы.

Нормы векторов и матриц. Обозначим через - точное решение системы, а через - приближенное решение системы. Для количественной характеристики вектора погрешности  введем понятие нормы.

Нормой вектора  называется число , удовлетворяющее трем аксиомам: 

1)  причем  = 0 тогда и только тогда, когда = 0;

2)  для любого вектора  и любого числа ;

3)  для любых векторов  и .

Наиболее употребительными являются следующие три нормы:

  ,    ,   .

Абсолютная и относительная погрешности вектора вводятся с помощью формул:

  и  .

Нормой матрицы  называется величина . Введенная норма обладает свойствами, аналогичными свойствам нормы вектора:

1)  причем  = 0 тогда и только тогда, когда  A = 0;

2)  для любой матрицы A и любого числа ;

3)  для любых матриц A и B;

4) .

Каждой из векторных норм соответствует своя подчиненная норма матрицы:

  ,    ,   .

В оценках вместо нормы  используется евклидова норма матрицы

  , так как   .

Абсолютная и относительная погрешности матрицы вводятся аналогично погрешностям вектора с помощью формул:

  ,   .

Пусть рассматривается система линейных алгебраических уравнений

В матричной форме записи она имеет вид . Будем предполагать, что матрица системы задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным.

Обусловленность задачи. Так же как и другие задачи, задача вычисления решения системы может быть как хорошо обусловленной, так и плохо обусловленной. 

Теорема об оценке погрешности решения по погрешностям входных данных.

Пусть решение системы , а x* - решение системы A*x*=b*, тогда , где  - относительное число обусловленности системы.

Если число обусловленности больше 10, то система является плохо обусловленной, так как возможен сильный рост погрешности результата.

Метод Гаусса. Рассмотрим метод Гаусса (схему единственного деления) решения системы уравнений. Прямой ход состоит из m-1 шагов исключения.

1 Шаг. Исключим неизвестное  из уравнений с номерами i = 2,3,..m. Предположим, что . Будем называть его ведущим элементом 1-го шага.

Найдем величины , i=2,3,...m , называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, ...m vго уравнений системы первое уравнение, умноженное соответственно на . В результате 1-го шага получим эквивалентную систему уравнений:

Аналогично проводятся остальные шаги. Опишем очередной k-ый шаг. Предположим, что ведущий элемент . Вычислим множители к-го шага:, i=k+1,...m и вычтем последовательно из (k+1)-го, ...m v го уравнений системы k-ое уравнение, умноженное соответственно на 

.После (m-1)-го шага исключения получим систему уравнений

,

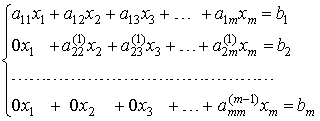матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы находим . Подставляя найденное значение  в предпоследнее уравнение, получим . Далее последовательно находим неизвестные .

LU  разложение матрицы. Представим матрицу A в виде произведения нижней треугольной матрицы L и верхней треугольной U.

Введем в рассмотрение матрицы 

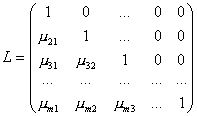 и

Можно показать, что A = LU. Это и есть разложение матрицы на множители.

Наверх

5. Решение систем линейных алгебраических уравнений прямыми методами.

Метод решения задачи называют прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Метод решения задачи называют итерационным, если в результате получают бесконечную последовательность приближений к решению. Если эта последовательность сходится к решению задачи, то говорят, что итерационный процесс сходится. К прямым методам решения относятся метод Гаусса и его модификации, метод Холецкого и метод прогонки.

В методе Гаусса для вычисления масштабирующих множителей требуется делить на ведущие элементы каждого шага. Если элемент равен нулю или близок к нулю, то возможен неконтролируемый рост погрешности.

Поэтому часто применяют модификации метода Гаусса, обладающие лучшими вычислительными свойствами.

Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент  при неизвестной  в уравнениях с номерами i = k+1, ... , m.Затем уравнение, соответствующее выбранному коэффициенту с номером , меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента . После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.

Метод Холецкого. Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU-разложения матрицы A, в результате чего она приводится к виду A=. Если разложение получено, то как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами:  и  . Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы  приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:

 ,  i = 2, 3, ..., m,

 ,  i = 3, 4, ..., m,

...............

     i = k+1, ... , m.

Метод прогонки.Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:

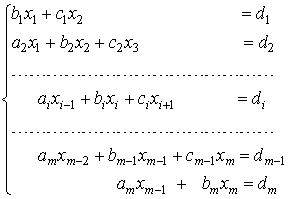
Преобразуем первое уравнение системы к виду , где ,

Подставим полученное выражение во второе уравнение системы и преобразуем его к виду  и т.д. На i-ом шаге уравнение преобразуется к виду , где , . На m-ом шаге подстановка в последнее уравнение выражения  дает возможность определить значение :

. Значения остальных неизвестных находятся по формулам: , i = m-1, m-2, ..., 1.

Наверх

6. Решение систем линейных алгебраических уравнений итерационными методами.

Рассматривается система Ax = b. 

Для применения итерационных методов система должна быть приведена к эквивалентному виду x=Bx+d. Затем выбирается начальное приближение к решению системы уравнений 

 и находится последовательность приближений к корню. Для сходимостиитерационного процесса достаточно, чтобы было выполнено условие . Критерий окончания итераций зависит от применяемого итерационного метода.

Метод Якоби.

Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное  x1, из второго уравнения системы выразим  x2, и т. д. В результате получим систему уравнений с матрицей B, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:

 ,i, j = 1, 2, ... n. 

Компоненты вектора d вычисляются по формулам:

 ,   i = 1, 2, ... n. 

Расчетная формула метода простой итерации имеет вид 

, 

или в покоординатной форме записи выглядит так:

,  i = 1, 2, ... m.

Критерий окончания итераций в методе Якоби имеет вид: 

 ,   где   .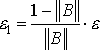 

Если  , то можно применять более простой критерий 

 окончания итераций 

Метод Зейделя.

Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестному  xi при i >1 используют уже найденные (n+1)-е приближения к неизвестным  x1, x2, ..., xi - 1, а не n-ое приближение, как в методе Якоби. Расчетная формула метода в покоординатной форме записи выглядит так:

, 

 i = 1, 2, ... m.. Условия сходимости и критерий окончания итераций можно взять такими же как в методе Якоби.

Пусть матрица системы уравнений A - симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается. 

Метод простой итерации.

Если A - симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду: 

x = x - (Ax - b),   - итерационный параметр. 

Расчетная формула метода простой итерации в этом случае имеет вид:

x (n+1) = x n -  (Ax n - b). 

Здесь B = E -  A  и параметр   > 0 выбирают так, чтобы по возможности сделать минимальной величину  . 

Пусть  и  - минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра  . В этом случае   принимает минимальное значение равное .

Наверх

7. Приближение функций. Метод наименьших квадратов.

На практике часто возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате эксперимента. Часто вид эмпирической зависимости известен, но числовые параметры неизвестны. 

Ниже рассматривается решение задачи приближения многочленами таблично заданной функции по методу наименьших квадратов и по методу интерполяции.

Постановка задачи приближения функции по методу наименьших квадратов. Пусть функция y=f(x) задана таблицей своих значений: , i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение (СКО) минимально.

Так как многочлен определяется своими коэффициентами, то фактически нужно подобрать набор кофициентов , минимизирующий функцию .

Используя необходимое условие экстремума, , k=0,1,-m получаем так называемую нормальную систему метода наименьших квадратов: , k=0,1,-m.

Полученная система есть система алгебраических уравнений относительно неизвестных . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.

Запишем нормальную систему наименьших квадратов для двух простых случаев: m=0 и m=2. При m=0 многочлен примет вид: . Для нахождения неизвестного коэффициента  имеем уравнение:. Получаем, что коэффициент  есть среднее арифметическое значений функции в заданных точках. 

Если же используется многочлен второй степени , то нормальная система уравнений примет вид:

Предположим, что функцию f можно с высокой точностью аппроксимировать многочленом некоторой степени m. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные  содержат случайные ошибки. Для решения этой задачи можно принять следующий алгоритм: для каждого m=0,1,2,.. вычисляется величина 

. За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина  стабилизируется или начинает возрастать.

Определение параметров эмпирической зависимости. Часто из физических соображений следует, что зависимость  между величинами хорошо описывается моделью вида , где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров из условия минимума функции: .

Если зависимость от параметров  нелинейна, то экстремум функции ищут методами минимизации функций нескольких переменных.

Наверх

8. Приближение функций. Интерполяция.

Постановка задачи интерполяции функций.

Пусть функция y = f(x) задана таблицей своих значений: 

, i=0,1,...n. Требуется найти многочлен степени n, такой, что значения функции и многочлена в точках таблицы совпадают:

, i=0,1,... n. 

Справедлива теорема о существовании и единственности интерполяционного многочлена.

Одна из форм записи интерполяционного многочлена - многочлен Лагранжа:

, где 

Многочлен представляет собой многочлен степени n , удовлетворяющий условию

 .

Таким образом, степень многочлена  равна n и при  в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером , равного . Поэтому многочлен Лагранжа является интерполяционным.

Другая форма записи интерполяционного многочлена - интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция f задана с произвольным шагом и

точки таблицы занумерованы в произвольном порядке. Величины 

 называют разделенными разностями первого порядка. Разделенные разности второго порядка определяются формулой:

.

Определение разделенной разности порядка таково: 

. 

Используя разделенные разности, интерполяционный многочлен Ньютона можно записать в следующем виде:

Величину называют погрешностью интерполяции или остаточным членом интерполяции.

Оценка погрешности интерполяции.

Если функция n+1 раз на отрезке [a,b] , содержащем узлы интерполяции , i=0,1,...n, то для погрешности интерполяции справедлива оценка: 

. Здесь , .

Эта оценка показывает, что для достаточно гладкой функции при фиксированной степени интерполяционного многочлена погрешность интерполяции стремится к нулю не медленнее, чем величина, пропорциональная . Этот факт формулируют так: интерполяционный многочлен степени nаппроксимирует функцию с (n+1) порядком точности относительно .

В практическом плане формула Ньютона обладает преимуществами перед формулой Лагранжа. Предположим, что в необходимо увеличить степень многочлена на единицу, добавив в таблицу еще один узел . При использовании формулы Лагранжа это приводит к необходимости вычислять каждое слагаемое заново. Для вычисления достаточно добавить к лишь очередное слагаемое: . Если функция f достаточно гладкая, то справедливо приближенное равенство . Это равенство можно использовать для практической оценки погрешности интерполяции :.

Наверх

9. Приближение функций. Сплайны.

Глобальная и кусочно-полиномиальная интерполяция. Пусть функция  f(x) интерполируется на отрезке [a,b]. Метод решения этой задачи с помощью единого многочлена  для всего отрезка называют глобальной полиномиальной интерполяцией. В вычислительной практике такой поход применяется редко в силу различных причин. Одна из причин v необходимо задать стратегию выбора узлов при интерполяции функции  f многочленами все возрастающей степени n.

Теорема Фабера. Какова бы ни была стратегия выбора узлов интерполяции, найдется непрерывная на отрезке [a,b] функция  f, для которой  при . Таким образом, теорема Фабера отрицает существование единой для всех непрерывных функций стратегии выбора узлов. Проиллюстрируем сказанное примером.

Предположим, что выбираем равноотстоящие узлы, то есть , i = 0,1,...n, где . Покажем, что для функции Рунге такая стратегия является неудачной.

На практике чаще используют кусочно-полиномиальную интерполяцию: исходный отрезок разбивается на части и на каждом отрезке малой длины исходная функция заменяется многочленом невысокой степени. Система Mathcad предоставляет возможность аппроксимации двумя важными классами функций: кусочно-линейной и сплайнами.

При кусочно-линейной интерполяции узловые точки соединяются отрезками прямых, то есть через каждые две точки  ,  проводится полином первой степени.

Как видно из приведенного примера этот способ приближения также имеет недостаток: в точках "стыка" двух соседних многочленов производная, как правило, имеет разрыв.

Если исходная функция была гладкой и требуется, чтобы и аппроксимирующая функция была гладкой, то кусочно-полиномиальная интерполяция неприемлема. В этом случае применяют сплайны v специальным образом построенные гладкие кусочно-многочленные функции.

Интерполяция сплайнами. Пусть отрезок [a,b] разбит точками на n частичных отрезков . Сплайном степени m называется функция , обладающая следующими свойствами:

1) функция  непрерывна на отрезке [a,b] вместе со своими производными до некоторого порядка  p.

2) на каждом частичном отрезке  функция совпадает с некоторым алгебраическим многочленом  степени m.

Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a,b] производной называют дефектом сплайна. Кусочно-линейная функция является сплайном первой степени с дефектом, равным единице. Действительно, на отрезке [a,b] сама функция  (нулевая производная) непрерывна. В то же время на каждом частичном отрезке  совпадает с некоторым многочленом первой степени.

Наиболее широкое распространение получили сплайны 3 степени (кубические сплайны)  с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.

Погрешность приближения кубическими сплайнами. Пусть функция f имеет на отрезке [a,b] непрерывную производную четвертого порядка и . Тогда для интерполяционного кубического сплайна справедлива оценка погрешности: .

Наверх

10. Решение задачи Коши одношаговыми методами.

Постановка задачи Коши для дифференциального уравнения первого порядка.

Пусть дано дифференциальное уравнение первого порядка  . Требуется найти функцию  , удовлетворяющую при  дифференциальному уравнению и при  начальному условию . 

Теорема существования и единственности задачи Коши. Пусть функция  определена и непрерывна на множестве точек  . Предположим также, что она удовлетворяет условию Липшица:  для всех  и произвольных ,  , где  - некоторая константа (постоянная Липшица). Тогда для каждого начального значения  существует единственное решение  задачи Коши, определенное на отрезке  .

Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Заданием начального условия мы выделяем из семейства решений ту единственную кривую, которая проходит через фиксированную точку

Численное решение задачи Коши методом Эйлера.

Численное решение задачи Коши состоит в построении таблицы приближенных значений в точках  . Точки ,  называются узлами сетки, а величина  - шагом сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной:  . Разрешая уравнение относительно  , получаем расчетную формулу метода Эйлера: , . 

Численный метод называется  явным, если вычисление решения в следующей точке осуществляется по явной формуле. Метод называется одношаговым, если вычисление решения в следующей точке  производится с использованием только одного предыдущего значения  . Метод Эйлера является явным одношаговым методом. 

Оценка погрешности метода Эйлера.

Локальной погрешностью метода называется величина  . Найдем величину локальной погрешности метода Эйлера:  , при условии, что  . Другими словами  погрешность, которую допускает за один шаг метод, стартующий с точного решения. Глобальной погрешностью   (или просто погрешностью) численного метода называют сеточную функцию  со значениями  в узлах. В качестве меры абсолютной погрешности метода примем величину  . Можно показать, что для явных одношаговых методов из того, что локальная погрешность имеет вид  следует, что  , где  и M - некоторые константы. Таким образом, метод Эйлера является методом первого порядка точности. Для нахождения решения задачи Коши с заданной точностью  требуется найти такое приближенное решение  , для которого величина глобальной погрешности  . Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.

Правило Рунге оценки погрешностей.  Для практической оценки погрешности проводят вычисления с шагами h и h/2. За оценку погрешности решения, полученного с шагом h/2, принимают величину, равную 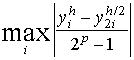 , где p - порядок метода.

Модификации метода Эйлера.

Метод Эйлера обладает медленной сходимостью, поэтому чаще применяют методы более высокого порядка точности. Второй порядок точности по  имеет усовершенствованный метод Эйлера : . Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом  ломаных, так как интегральная кривая на отрезке  заменяется ломаной с угловым коэффициентом  . В усовершенствованном методе Эйлера интегральная кривая на отрезке  заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка  . Так как значение  в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом . 

Еще одна модификация метода Эйлера второго порядка - метод Эйлера-Коши:

Решение систем дифференциальных уравнений методом Эйлера.

Пусть требуется решить нормальную систему дифференциальных уравнений: 

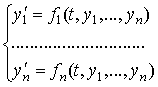
с начальными условиями: ,  , ...,

Эту систему в векторной форме можно записать в виде: ,  . Здесь 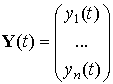, ,  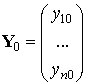. Расчетная формула метода Эйлера имеет вид: , .