MATLAB и быстрое преобразование Фурье

В этой статье я постараюсь объяснить, что же все-таки выдает в качестве результата fft (Fast Fourier transform) на примере MATLAB (и в качестве бонуса проведу небольшой ликбез по этому весьма полезному, на мой взгляд, языку).

По работе неоднократно сталкивался с необходимостью быстро определить наличие в сигнале гармонических составляющих. Часто для примерной оценки достаточно воспользоваться алгоритмом быстрого преобразования Фурье. Тем более что его реализации есть практически во всех математических пакетах и библиотеках, да и собственноручно реализовать не составит особого труда. Между тем, опыт показывает, что при всей своей простоте метод начинает вызывать некоторые вопросы, когда возникает необходимость не просто посмотреть наличие дискреток в сигнале, но и выяснить их абсолютные значения, т.е. нормализовать полученный результат.

В этой статье я постараюсь объяснить, что же все-таки выдает в качестве результата fft (Fast Fourier transform) на примере MATLAB (и в качестве бонуса проведу небольшой ликбез по этому весьма полезному, на мой взгляд, языку).

MATLAB позволяет не заморачиваться с ручным удалением ненужных объектов, однако при работе с более-менее объемными массивами данных имеет привычку капризничать и жаловаться на недостаток памяти. Для освобождения памяти используется процедура clear с указанием имени объекта, который необходимо удалить.

С этого и начнем. Так как все необходимое мы сгенерируем самостоятельно, можно смело удалять все, что накопилось в рабочем пространстве за активную сессию, просто добавив ключевое слово all:

clear all% Очистка памяти

Итак, прежде всего зададим исходные данные для нашей модели. Фурье анализ идеально подходит для выделения гармонических сигналов на фоне помех. Для того чтобы продемонстрировать это, возьмем в качестве сигнала сумму некоторой постоянной и двух синусоид с разной частотой и амплитудой. Дисперсию шума возьмем в 3 раза больше амплитуды первой синусоиды. Также зададим количество частотных полос, которые должен будет посчитать fft алгоритм. Точка с запятой в конце строк не обязательна, и если ее не ставить, результат вычисления функций и задания переменных будет дублироваться в командную строку, что можно использовать для отладки кода (однако 512 значений сплошным полотном в командной строке вряд ли помогут вам, тем более что их вывод тоже занимает некоторое количество времени, так что все же лучше не забывать закрывать строки).

%% Параметры
Tm=5;% Длина сигнала (с)
Fd=512;% Частота дискретизации (Гц)
Ak=0.5;% Постоянная составляющая (Попугаев)
A1=1;% Амплитуда первой синусоиды (Попугаев)
A2=0.7;% Амплитуда второй синусоиды (Попугаев)
F1=13;% Частота первой синусоиды (Гц)
F2=42;% Частота второй синусоиды (Гц)
Phi1=0;% Начальная фаза первой синусоиды (Градусов)
Phi2=37;% Начальная фаза второй синусоиды (Градусов)
An=3*A1;% Дисперсия шума (Попугаев)
FftL=1024;% Количество линий Фурье спектра


MATLAB (Matrix Laboratory), как следует из названия, предназначен прежде всего для работы с массивами, практически все алгоритмы счета в нем оптимизированы для работы с векторами. Обилие удобных инструментов работы так же ненавязчиво подталкивает представлять как можно больше исходных данных в виде матриц. В частности, можно легко сгенерировать массив возрастающих (убывающих) величин с заданным шагом (1\Fd в данном примере):

%% Генерация рабочих массивов
T=0:1/Fd:Tm;% Массив отсчетов времени


Случайный Гауссов шум задается функцией randn, результатом которой является массив размерности, заданной в ее параметрах. Для единообразия зададим его в виде строки (первый параметр 1) длиной соответствующей длине нашего массива отсчетов времен, что в свою очередь вычислим функцией length.

Noise=An*randn(1,length(T));% Массив случайного шума длиной равной массиву времени

Символ * используется для обозначения перемножения. Т.к. чаще всего действия производятся над векторами, то и умножение подразумевается векторное, но так же легко можно, не перегружая этот оператор, использовать его для поэлементного перемножения, добавив перед ним точку (.*). При умножении вектора на скаляр точка перед умножением не является обязательной. Также добавленная точка сделает поэлементным возведение в степень и деление.

Signal=Ak+A1*sind((F1*360).*T+Phi1)+A2*sind((F2*360).*T+Phi2);% Массив сигнала (смесь 2х синусоид и постоянной составляющей)

Теперь перейдем к тому, ради чего и затевалась данная статья — функции fft(). Аргументами стандартной функции MATLAB являются сам сигнал (в нашем случае Signal), размерность вектора-результата (FftL), а также измерение.
Последний аргумент определяет вдоль какого измерения располагается сигнал, в случае если на вход подается многомерный массив (иногда этот параметр ошибочно принимают за размерность преобразования Фурье, но это не так. Хотя в MATLAB есть реализации двухмерного fft2() и многомерного fftn() алгоритмов). Так как наш сигнал представляет собой вектор, то его вполне можно опустить.
Рассмотрим сначала сигнал без примеси шума. В качестве результата мы получим вектор комплексных чисел. Это и есть представление нашего сигнала в частотном домене в показательной форме. Т.е. модули этих комплексных чисел представляют амплитуды соответствующих частот (точнее полосы частот см. дальше), а аргументы – их начальные фазы. И если полученная фаза, однозначно вычисляется в радианах, то с амплитудой и частотами не все так просто.
Например, если мы просто применим к нашему сигналу преобразование Фурье, и возьмем абсолютные значения вектора на выходе, то получим приблизительно следующую картинку:

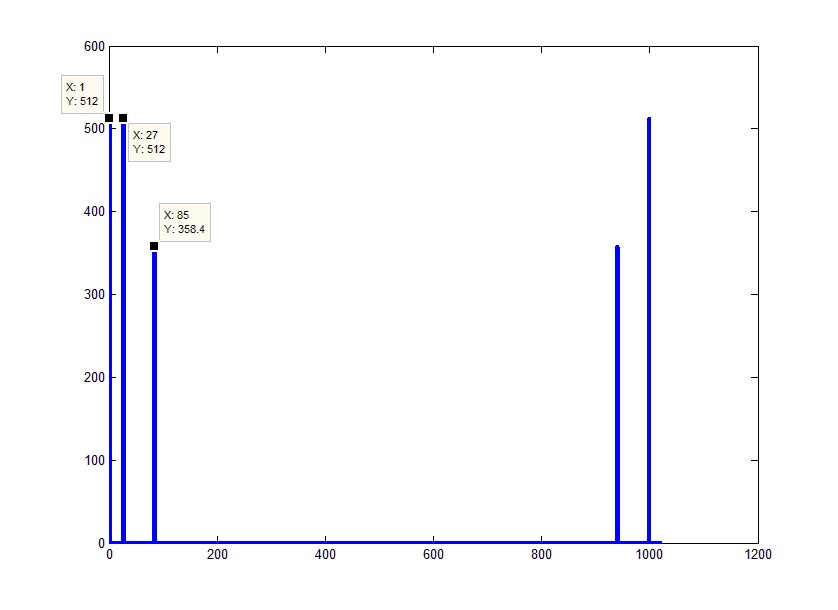
Для построения двухмерных графиков удобно использовать функцию plot. Основные параметры, используемые в этой функции, – одномерные массивы точек, первый задает ось ординат, второй – значение функции в соответствующих точках. Если передать только один массив, то он будет отображен с фиксированным шагом 1.
Если присмотреться к полученной картинке, выяснится, что она несколько отличается от наших ожиданий. На приведенном графике 5 пиков вместо ожидаемых 3х (постоянная + 2 синусоиды), их амплитуды не совпадают с амплитудами исходных сигналов, и ось абсцисс вряд ли отображает частоты.

Прежде всего, следует учитывать, что счет алгоритма устроен таким образом, что перебираются не только положительные, но и отрицательные частоты и правая часть графика является «зеркальным» отображением реального спектра. Т.е. на самом деле 0 (которому соответствует постоянная часть сигнала) должен приходиться на середину массива. Ситуацию можно поправить, совершив циклический сдвиг на половину длины массива. Для этих целей в MATLAB существует функция сдвига fftshift(), смещающая первый элемент в середину массива:

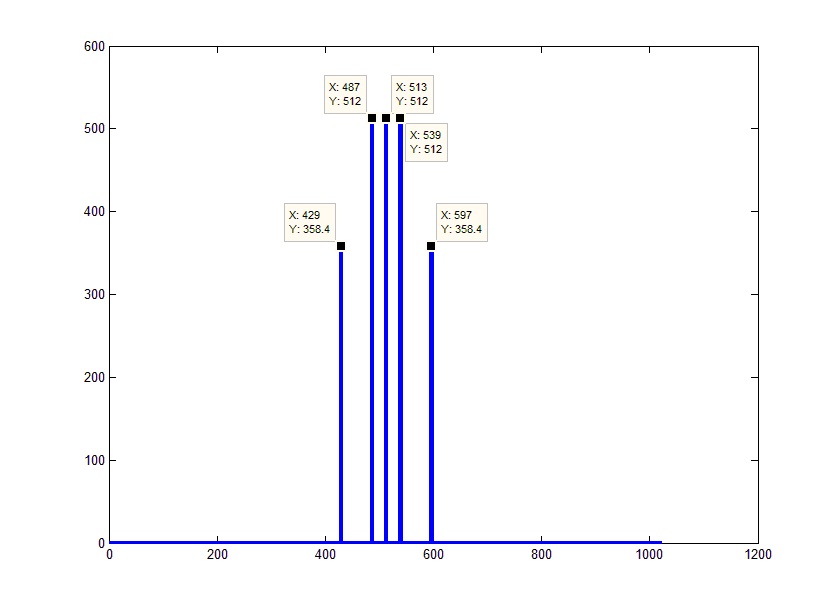
Теперь обратим внимание на ось значений.
Согласно теореме отсчетов (также известной как теорема Найквиста-Шеннона или более патриотично теорема Котельникова) спектр дискретного сигнала будет ограничен половиной частоты дискретизации (Fd). Или в нашем случае –Fd/2 слева и Fd/2 справа. Т.е. весь полученный массив покрывает Fd частот. Отсюда, учитывая что мы знаем (вернее даже самостоятельно задали в качестве параметра) длину массива, получим частоты в виде массива значений от –Fd/2 до Fd/2 с шагом Fd/FftL (на самом деле крайняя правая частота будет меньше границы на один отсчет т.е. Fd/2-Fd/FftL):

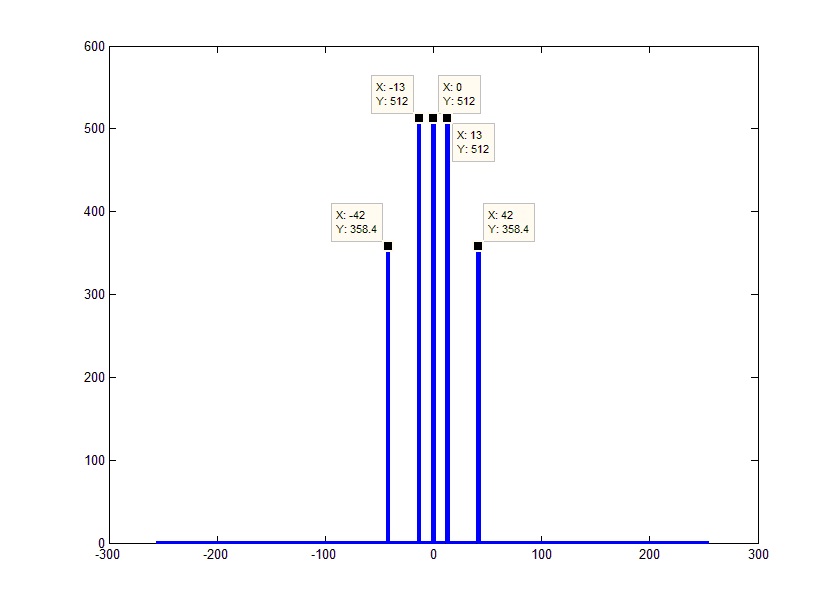
Если посмотреть на фазы частот, можно заметить, что они равны отрицательным фазам соответствующих отрицательных частот. Учитывая равенство амплитуд левой и правой частей спектра и соответствие их фаз с точностью до знака, весь спектр будет эквивалентен своей положительной части с удвоенной амплитудой. Исключение составляет только 0 элемент, который не имеет зеркальной половины. Таким образом, можно избавиться от «непонятных» и зачастую ненужных отрицательных частот. Это можно было сделать сразу просто отбросив конец исходного массива и помножив оставшиеся элементы на 2 (за исключением постоянной составляющей):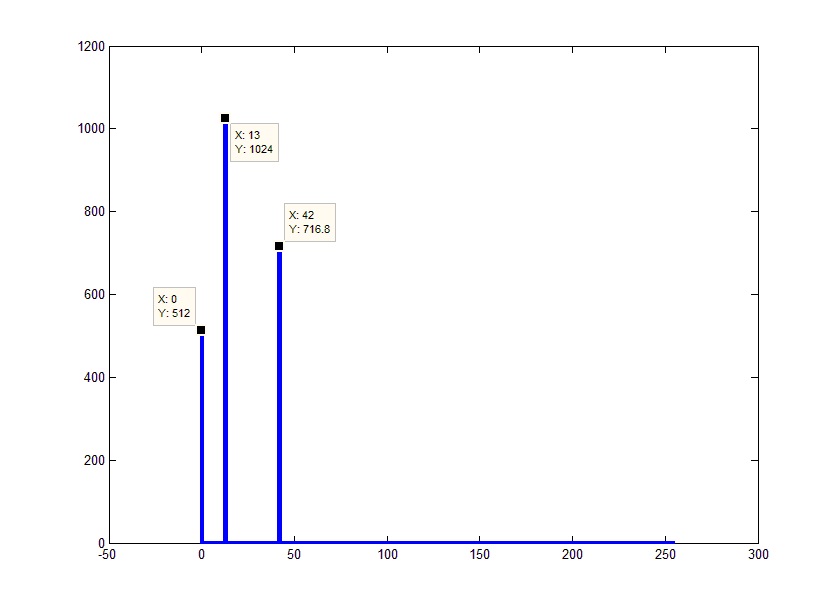



Теперь это уже похоже на тот результат, который мы ожидаем. Единственное, что смущает теперь – это амплитуды. С этим все достаточно просто. Т.к. быстрое преобразование Фурье фактически представляет собой суммирование сигнала перемноженного на ядро преобразования (комплексную экспоненту) для каждой из частот, то реальный результат будет меньше полученного ровно в количество суммирований (частот в результате), т.е. полученный результат надо разделить на количество элементов в результате (не забываем, что под результатом понимается весь ответ, вместе с отброшенной частью, т.е. наше заданное FftL):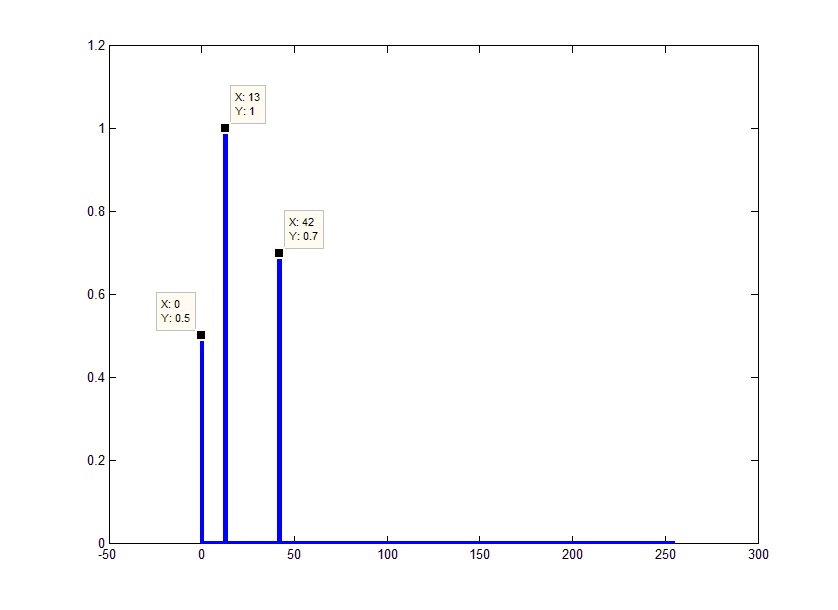



Стоит упомянуть еще одну вещь. В спектральном представлении вычисляется не значение сигнала на той частоте, на которую попал алгоритм (как мы помним, частоты следуют с шагом Fd/FftL), а значение в полосе (шириной равной шагу). Т.е. если в эту полосу попало несколько дискреток, то они суммируются. Для примера можно уменьшить количество линий в результате работы алгоритма: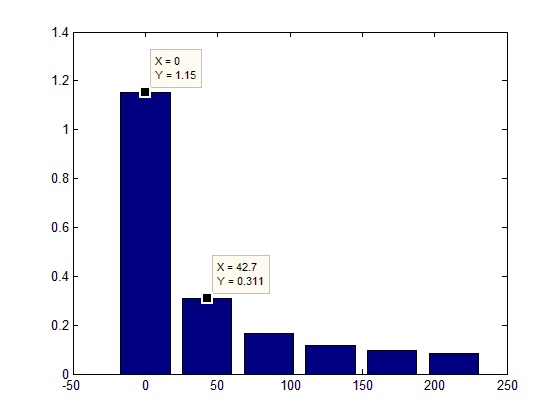



Однако это не означает, что стоит сразу бездумно увеличивать точность работы, т.к. это тоже приводит к негативным последствиям, т.к. если разрешение будет сопоставимо с частотой дискретизации сигнала, в спектр полезут гармоники «окна», которые имеют отношение не к реальному сигналу, а к его дискретному представлению: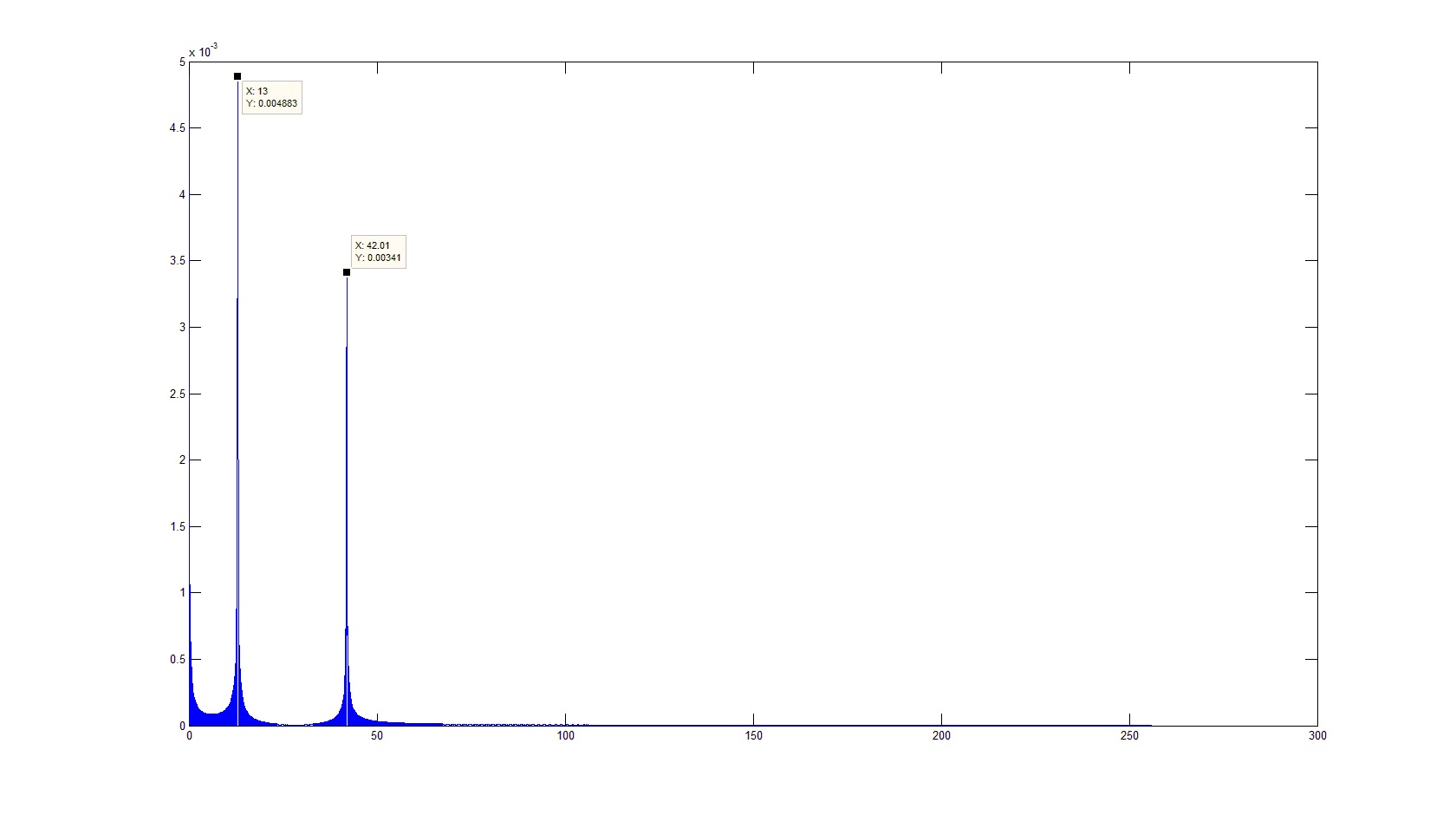



Или более близко окрестности одной из дискреток: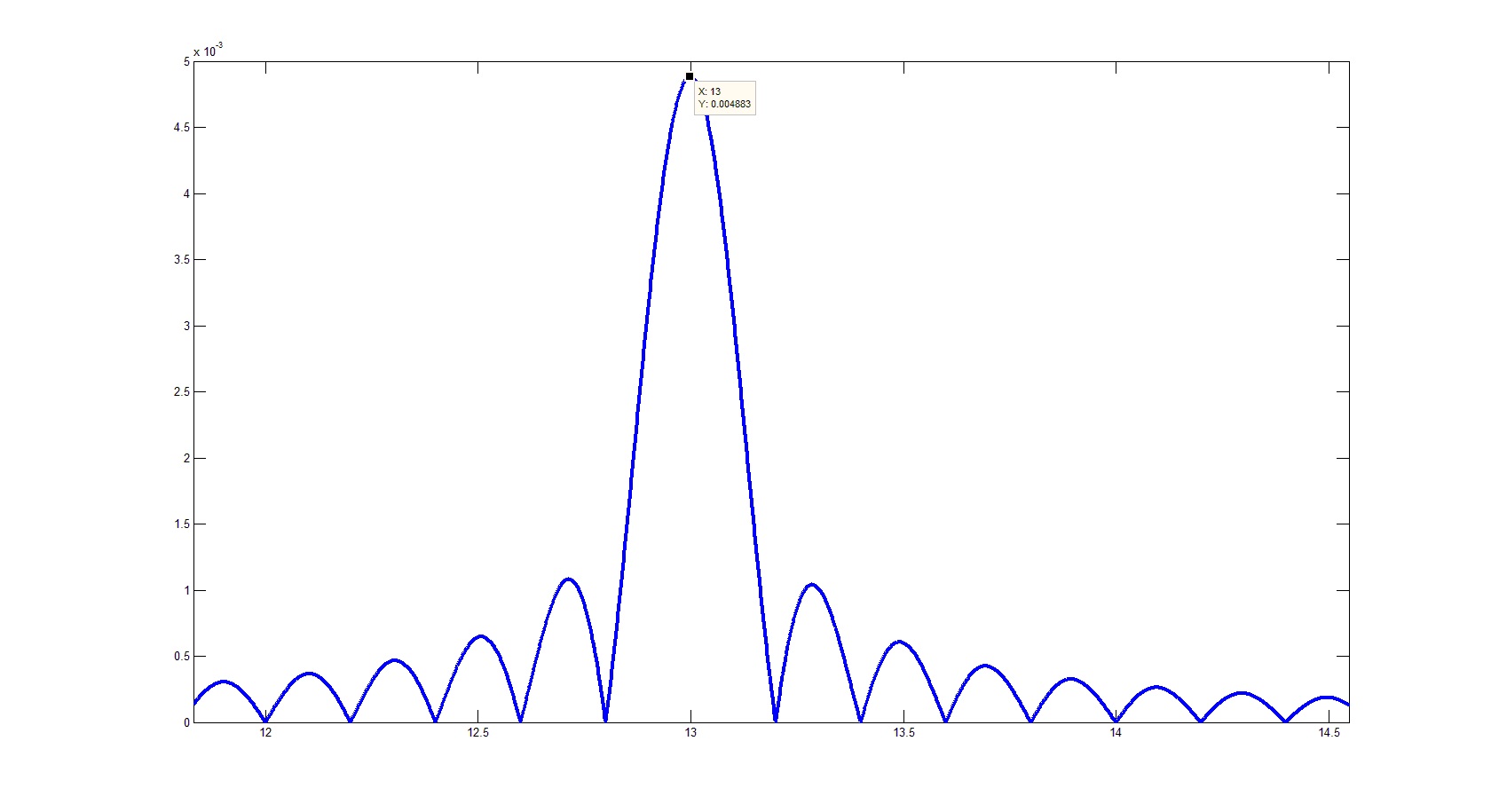



Код для нормировки fft будет выглядеть приблизительно следующим образом:

%% Спектральное представление сигнала
FftS=abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала
FftS=2*FftS./FftL;% Нормировка спектра по амплитуде
FftS(1)=FftS(1)/2;% Нормировка постоянной составляющей в спектре
FftSh=abs(fft(Signal+Noise,FftL));% Амплитуды преобразования Фурье смеси сигнал+шум
FftSh=2*FftSh./FftL;% Нормировка спектра по амплитуде
FftSh(1)=FftSh(1)/2;% Нормировка постоянной составляющей в спектре


Нам осталось только вывести результаты. Функция subplot позволяет разбить окно на несколько областей для отображения графиков.

%% Построение графиков
subplot(2,1,1);% Выбор области окна для построения
plot(T,Signal);% Построение сигнала
title('Сигнал');% Подпись графика
xlabel('Время (с)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
plot(T,Signal+Noise);% Построение смеси сигнал+шум
title('Сигнал+шум');% Подпись графика
xlabel('Время (с)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика

F=0:Fd/FftL:Fd/2-1/FftL;% Массив частот вычисляемого спектра Фурье
figure% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
plot(F,FftS(1:length(F)));% Построение спектра Фурье сигнала
title('Спектр сигнала');% Подпись графика
xlabel('Частота (Гц)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
plot(F,FftSh(1:length(F)));% Построение спектра Фурье сигнала
title('Спектр сигнала');% Подпись графика
xlabel('Частота (Гц)');% Подпись оси х графика
ylabel('Амплитуда (Попугаи)');% Подпись оси у графика


Результат выполнения кода будет выглядеть следующим образом: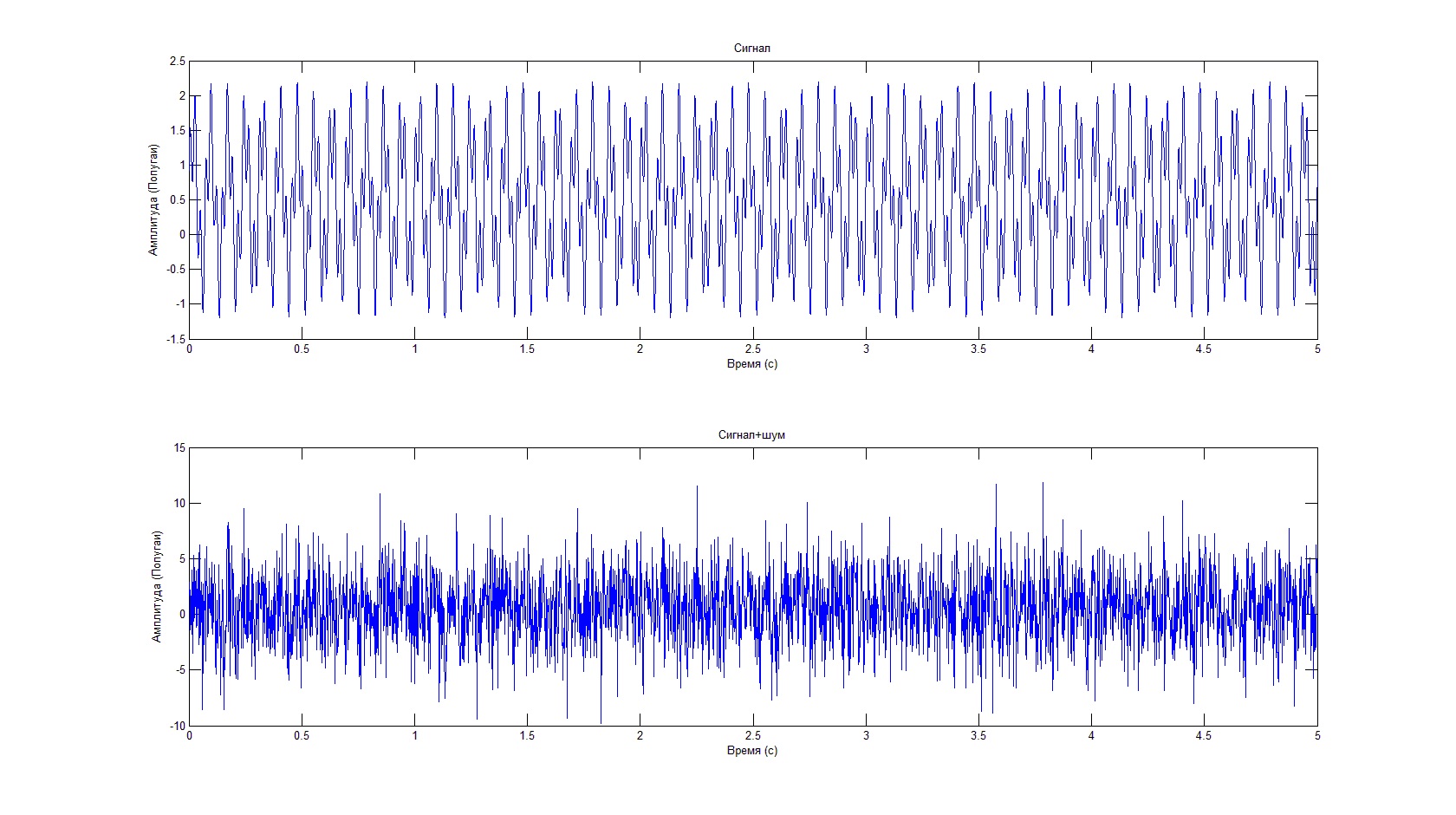





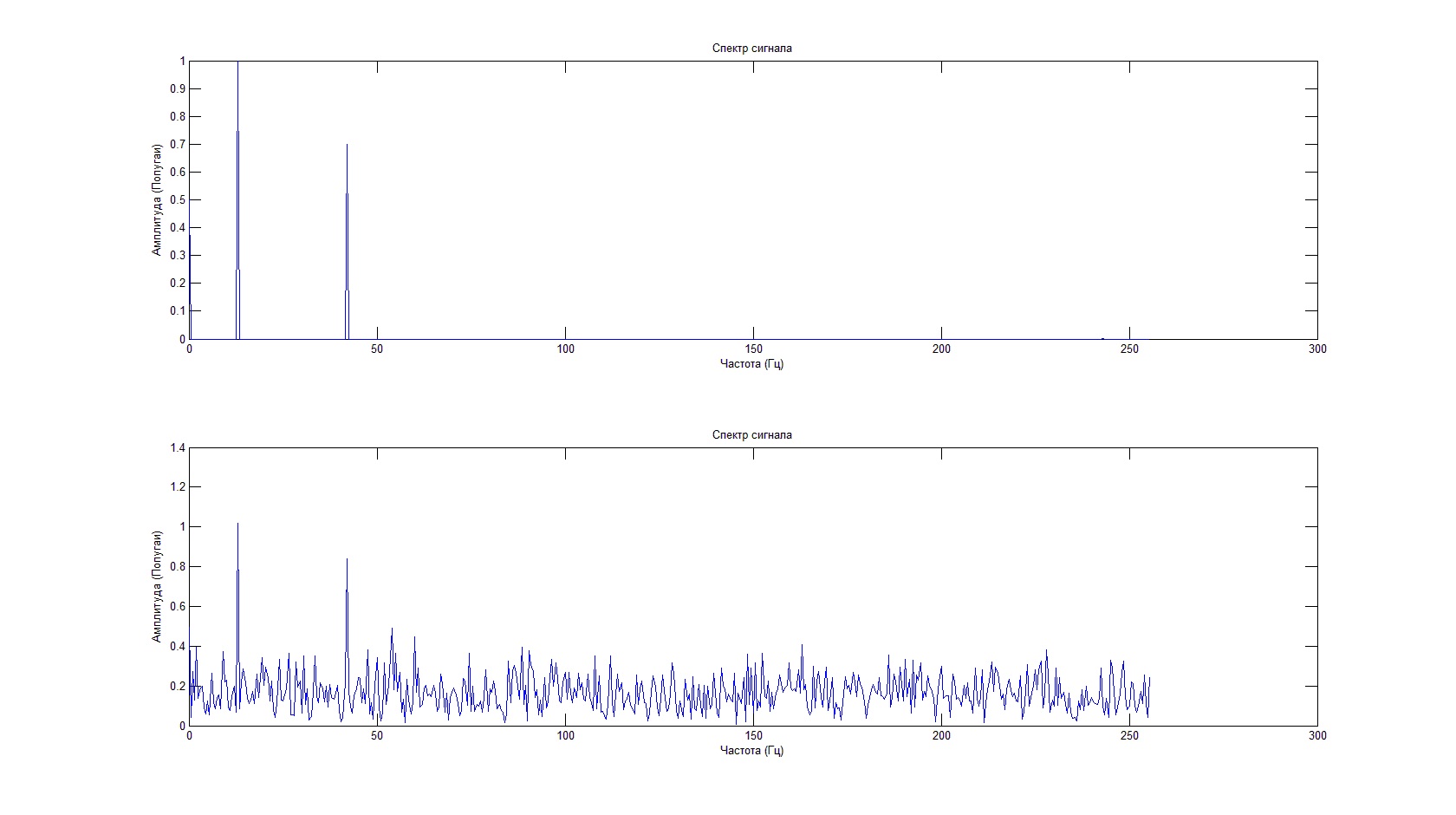
Несмотря на то, что полезного сигнала не видно на фоне шума, спектральная характеристика позволяет определить его частоту и амплитуду.

Надеюсь, данный текст был вам полезен.