Авторы - В.Д.Борисевич, В.Г.Потемкин, С.П.Струнков

В настоящее время численное моделирование прочно вошло в практику работы научно-исследовательских, проектно-конструкторских и производственных учреждений во всем мире. Правительства многих стран на стадии разработки проекта обязывают своих производителей создавать полностью компьютерные модели будущих высокотехнологичных изделий. Многочисленные успехи в освоении космоса и выборе рациональных форм летательных аппаратов, практике оптимального управления и разработке различных высоких технологий в немалой степени обязаны проведению так называемых вычислительных экспериментов и использованию полученной таким образом информации. При правильно поставленной, хорошо смоделированной и рационально алгоритмизированной задаче объем информации, который получается из расчетов, зачастую значительно полнее и стоит дешевле существующих экспериментальных исследований.

Оглавление

Введение

1. Математические основы

1.1. Прямоугольные и квадратные матрицы, ранги, жордановы формы

1.2. Регулярные и сингулярные пучки матриц. Каноническая форма Кронекера

1.3. Квазитреугольная форма сингулярных пучков

2. Решение СНАУ

2.1. Спектральный метод решения СНАУ

2.2. Алгоритм решения СНАУ

2.3. Протокол решения тестовой системы

Список литературы

 

Наверх

Введение

В настоящее время численное моделирование прочно вошло в практику работы научно-исследовательских, проектно-конструкторских и производственных учреждений во всем мире. Правительства многих стран на стадии разработки проекта обязывают своих производителей создавать полностью компьютерные модели будущих высокотехнологичных изделий. Многочисленные успехи в освоении космоса и выборе рациональных форм летательных аппаратов, практике оптимального управления и разработке различных высоких технологий в немалой степени обязаны проведению так называемых вычислительных экспериментов и использованию полученной таким образом информации. При правильно поставленной, хорошо смоделированной и рационально алгоритмизированной задаче объем информации, который получается из расчетов, зачастую значительно полнее и стоит дешевле существующих экспериментальных исследований.

Современные компьютеры с процессорами, эффективно реализующими вычисления как целочисленные, так и с плавающей запятой, позволяют проводить прямое численное моделирование сложных задач, связанных с решением нелинейных дифференциальных уравнений в частных производных. При численном моделировании осуществляется переход от так называемой непрерывной модели, выражающейся в записи исходной системы дифференциальных уравнений и граничных условий, к дискретной модели, представляющей собой систему нелинейных алгебраических уравнений (СНАУ) большой размерности, получаемую на основе различных разностных схем исследуемых уравнений. Такой переход необходим вследствие того, что в вычислительных методах отсутствует возможность непосредственной реализации многих математических операторов. Поэтому в дискретных моделях дифференцирование аппроксимируется разностными операторами, интегрирование - суммированием и т.д. 

Потребности практики вызвали интенсивную разработку методов вычислительной математики и, в частности, методов решения СНАУ вида

,

где fi - полиномы от переменных x1, ..., xn. 

Используемые в настоящее время методы решения систем нелинейных алгебраических уравнений (СНАУ) могут быть классифицированы как символьные и числовые. Символьные методы, чаще всего основанные на приведении к базису Грёбнера, используют механизм исключения переменных для сведения к задаче нахождения корней полиномов от одной переменной. Однако используемые в настоящее время алгоритмы для решения символьными методами эффективны только для систем полиномиальных уравнений низкого порядка (не выше, чем три или четыре). Главная проблема связана с плохой обусловленностью задачи вычисления корней полиномов с одной переменной степени больше, чем 14 или 15. Это обстоятельство во многих случаях не позволяет использовать эти методы в арифметике с фиксированной точностью из-за медленной сходимости соответствующих алгоритмов.

Числовые методы решения СНАУ, как правило, основаны на итерационных методах. Итерационные методы, такие как хорошо известный метод Ньютона, удовлетворительно работают только в области, достаточно близкой от решения и при задании хорошего начального приближения, что довольно трудно обеспечить на практике. 

Принципиально новый подход к решению СНАУ на основе спектрального разложения сингулярных пучков матриц был впервые описан в 1978 г. в работе В. Н. Кублановской [1]. В то время он не получил широкого распространения, поскольку не были разработаны эффективные вычислительные алгоритмы для определения канонических форм Кронекера (KФК) для прямоугольных пучков матриц. В 80-е гг. Ван Доорен доказал ряд теорем, связанных со спектральной структурой матричных пучков [2], продемонстрировав возможность приведения сингулярного пучка к квазитреугольной форме, содержащей два блока, первый из которых объединяет все бесконечные собственные значения и правые полиномиальные индексы, а второй - конечные собственные значения и левые полиномиальные индексы.

Новый подход к решению СНАУ, основанный на спектральном разложении матричных пучков, не использует информацию о якобиане системы и не требует линеаризации, характерной для итерационных методов типа метода Ньютона. Метод основывается на свойстве алгебраической структуры вектора переменных исходной СНАУ, что позволяет построить систему спектральных задач (ССЗ) для прямоугольных пучков матриц. При этом решения СНАУ определяются как собственные значения регулярных блоков матричных пучков.

В последние годы подход В. Н. Кублановской получил своё дальнейшее развитие в работах [3, 4], в которых представлены практические алгоритмы решения СНАУ и продемонстрировано их применение для решения ряда физических задач.

Настоящее пособие посвящено описанию пакета прикладных программ SNAE, разработанного для решения систем нелинейных алгебраических уравнений от двух переменных методом спектрального разложения сингулярных пучков матриц. Обсуждению разработанного алгоритма и примеров решения с его помощью задач предшествует необходимая для их практического освоения информация о прямоугольных матрицах и пучках матриц.

 

Наверх

Математические основы

1.1. Прямоугольные и квадратные матрицы, ранги, жордановы формы

Система строк (столбцов) матрицы 

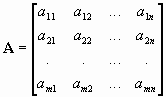(1.1)

называется базисной системой строк (столбцов), если она сама линейно независима, а система строк (столбцов), полученная присоединением к ней дополнительных строк (столбцов), уже является линейно зависимой. В курсе линейной алгебры доказывается, что число строк r , входящих в любую базисную систему строк, не зависит от выбора этой базисной системы и называется рангом матрицы A по строкам. Аналогичный факт верен также для базисных столбцов матрицы A и при этом ранги матрицы по строкам и по столбцам равны, и это общее число называется рангом матрицы A.

Чаще всего ранг матрицы вычисляют с помощью элементарных преобразований. Элементарными преобразованиями строк называются следующие преобразования:

1.  перестановка местами любых строк;

2.  умножение всех элементов строки на любое ненулевое число;

3.  прибавление к элементам какой-нибудь строки соответствующих элементов любой другой строки;

4.  вычеркивание нулевых строк, т.е. строк все элементы которых равны нулю.

5. Элементарные преобразования столбцов определяются аналогично. Элементарные преобразования строк и столбцов не меняют ранга матрицы. Легко проверить, что преобразования 1-3 можно реализовать при помощи умножения матрицы A справа на какую-нибудь невырожденную квадратную матрицу размера m x m. Опишем метод вычисления ранга матрицы с помощью элементарных преобразований строк. Заметим, что обычно к преобразованиям 1-4), определенным выше, добавляют еще одно преобразование перестановки любых столбцов матрицы. 

На первом шаге (после вычеркивания нулевых строк) выбирают максимальный по модулю (т.е. главный) элемент матрицы A и преобразованиями 1, 5 переводят его в левый верхний угол матрицы A, т.е. на позицию А(1, 1). Затем преобразованиями 2, 3 делают нулевыми все элементы первого столбца, кроме выбранного. Затем (снова после вычеркивания нулевых строк, если они есть) выбирают главный элемент среди элементов (новых) строк и столбцов преобразованной (на первом шаге) матрицы A, номера которых больше числа 1, и преобразованиями 1, 5 помещают его на позицию А(2, 2). После этого преобразованиями 2, 3 добиваются того, чтобы все элементы во втором столбце во всех строках, начиная с третьей, стали равными нулю и т.д. 

В результате таких преобразований получается матрица, все диагональные элементы которой отличны от нуля, а элементы, стоящие под диагональю, равны нулю. Число строк r полученной матрицы равно рангу заданной матрицы A.

Будем использовать следующие фундаментальные свойства ранга матрицы:

1. 
   

   1. для любой матрицы A размера m x n и любых невырожденных матриц B и C размеров соответственно
      m xm и n x n ранги матриц A и BAC совпадают;

   2. размерность пространства решений следующей линейной однородной системы уравнений с матрицей системы A

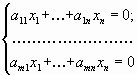(1.2)

равна n - rank(A). Систему вида (1.2) коротко будем записывать в виде Ax = 0.

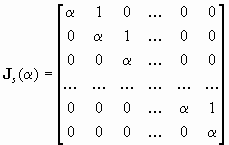
Жордановой клеткой порядка s называется матрица

, (1.3)

где a - некоторое комплексное число.

Будем говорить, что данная квадратная матрица J является матрицей Жордана, если она квазидиагональная и при этом ее диагональные блоки являются клетками Жордана .

В курсе линейной алгебры доказывается, что любая квадратная матрица A может быть приведена к жордановой форме, т.е. для нее существует невырожденная матрица C, такая, что матрица C-1AC является матрицей Жордана. При этом две различные жордановы формы матрицы A имеют одни и те же клетки Жордана, только порядок их расположения может отличаться. Легко видеть, что числа a i жордановых клеток жордановой формы J = C-1ACматрицы A являются ее характеристическими числами. При этом из приведенных выше свойств ранга матриц вытекает, что число всех жордановых клеток квадратной матрицы A порядка n, диагональные элементы которых равны нулю, составляет n - rank(A). Это число совпадает с размерностью пространства решений линейной системы однородных уравнений Ax = 0.

 

Наверх

1.2. Регулярные и сингулярные пучки матриц. Каноническая форма Кронекера

Пусть a, b - заданные матрицы размера m x n с вещественными или комплексными коэффициентами. Пучком матриц aи b называется матрица a - l b, элемент которой (a - l b)ij является функцией от l ; он также может быть записан в форме aij - l bij. Если m = n (т.е. матрицы a и b - квадратные) и определитель det(a - l b) не равен тождественно нулю, то пучок a - l b называется регулярным. В противном случае он называется сингулярным. Опишем канонические формы произвольных регулярных и сингулярных пучков, т.е. наиболее простой вид матрицы M(a - l b)N, где M и N - квадратные невырожденные матрицы размеров m x m и n x n соответственно. Для формулировки результатов нам понадобятся некоторые понятия теории матричных пучков.

В работах [5, 6] показано, что любой сингулярный пучок матриц a - l b приводится к канонической форме Кронекера

M(a - l b)N = diag{Zlr, , , 

, ..., , l E - J}, (1.4)

где присутствие Zlr означает, что первые l строк и r столбцов матрицы M(a - l b)N нулевые; Ll - двухдиагональный пучок размера (l+1) x 1 вида

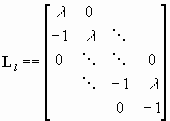, (1.5)

при этом числа l1, ..., ls и r1, ..., rt равны степеням левых и правых линейно независимых полиномиальных решений минимальных степеней однородных систем yT(l ) (a - l b) = 0, (a - l b) x(b) = 0 и называются левыми и правыми минимальными индексами соответственно; Ei - единичная матрица размера i x i; Ni - матрица размера i x i, в которой элементы (Ni)j j+1 = 1, а все остальные элементы равны нулю (каждый такой блок Ei - l Ni называется жордановой клеткой с бесконечным характеристическим числом и обозначается Ji(); E - единичная матрица; J - матрица Жордана.

Заметим, что число u жордановых клеток Ji() равно размерности подпространства Ker(b) решений системы bx = 0 и, следовательно, u = n - rank(b). Точно так же, число v жордановых клеток с нулевыми характеристическими числами в жордановой матрице J равно размерности пространства Ker(a) решений системы ax = 0, т.е. v = n - rank(a).

Задача приведения произвольного сингулярного пучка к канонической форме Кронекера довольно трудна. Однако для решения СНАУ часто бывает достаточно привести пучок к некоторой промежуточной форме. Ниже мы опишем одну такую форму и соответствующий алгоритм ее получения.

 

Наверх

1.3. Квазитреугольная форма сингулярных пучков

Рассмотрим сингулярный пучок a - l b размера m x n. Пусть X и Y - подпространства, принадлежащие Cn и Cmсоответственно, причем

Y = aX + bX. (1.6)

Выделим подпространства X и Y размерности l и k. Построим для них унитарные блочные матрицы Q и Z

  (1.7)

порядков n и m, соответственно, такие, что

X = <Z1>; Y = <Q1>. (1.8)

Как следует из (1.6), , где ( )H обозначает эрмитово сопряжение. Таким образом, справедливо соотношение

. (1.9)

Описанное здесь приведение к квазитреугольному виду будем называть элементарным. Важно отметить, что элементарные приведения осуществляются при помощи унитарных (или ортогональных) матриц Q и Z.

Используем теперь эти рассуждения для описания алгоритма приведения сингулярного пучка a -l b к квазитреугольному виду

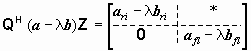, (1.10)

в котором каноническая форма Кронекера блока ari -l bri содержит все элементарные блоки вида Ji( ) и LiT пучка 

a - l b, а остальные элементарные блоки (т.е. блоки вида Li и l E - J) входят в состав формы Кронекера блока 

afl - l bfl. Для простоты будем считать, что между строками и столбцами матрицы a - l b нет постоянных линейных зависимостей, т.е. в канонической форме Кронекера отсутствует блок Zlr. Алгоритм приведения пучка к такому квазитреугольному виду предложен в работе [6]. Такое приведение получается последовательностью элементарных приведений, описанных выше, поэтому матрицы Q и Z, с помощью которых осуществляется это приведение, являются унитарными (или ортогональными). Это обстоятельство гарантирует устойчивость алгоритма. 

Пусть X = Ker(b), Y = aX - соответствующее разложение вида (1.9). Тогда каноническая форма Кронекера пучка 

c22 - l d22 содержит те же блоки вида Li и l E - J и в том же количестве, что и пучок a - l b. Такое разложение можно получить с помощью следующего построения. 

Выберем матрицу Z так, что <Z1> = Ker(b); полагая n1 = dim Ker(b), имеем

. (1.11)

Выберем Q так, что <Q1> = Im(X) = aX; полагая m1 = dim Im(X) , имеем

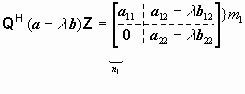, (1.12)

Теперь шаг (1.11-1.12) можно повторить для пучка a22 - l b22. Последовательное выполнение этих операций эквивалентно одному приведению, в котором унитарная матрица Z = [Z1 | Z2 |...], где <Z2> = Ker(b22). При этом 

n2 = dim Ker(b22) <= m1, так как в противном случае подпространство Ker(b22) = <Z2> будет содержать столбцы, принадлежащие подпространству Ker(b12) = <Z1>. Соответствующая матрица Q строится аналогично. Продолжая таким образом процесс приведения до тех пор, пока на некотором шаге l не образуется пучок al+1,l+1 - l bl+1,l+1, для которого Ker(bl+1,l+1) = {0} [7]. После этого процесс приведения прекращается и в результате получаем матрицу 

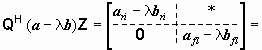
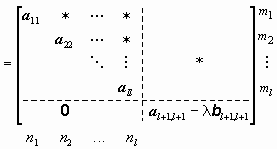(1.13)

При этом выполняются следующие неравенства

. (1.14)

При решении СНАУ, как правило, выполняется условие m = rank[a b], и тогда квазитреугольная форма для матричного пучка приобретает вид

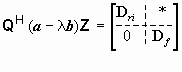. (1.15)

Эта структура имеет единственный блок Df с конечными собственными значениями и не имеет блока Dl, соответствующего левым полиномиальным решениям. Это позволяет использовать RGSVD (Reiterative General Singular Value Decomposition) - алгоритм [8] для выделения регулярного блока из матричного пучка.

 

Наверх

Решение СНАУ

Предлагаемый метод решения СНАУ сводит исходную проблему к спектральным задачам или системам спектральных задач (ССЗ) для сингулярных пучков прямоугольных матриц. 

В случае двух переменных ССЗ описывается следующим образом

(2.1)

где D(x) = (ax - x bx), D(y) = (ay - y by) - пучки матриц; Rx(x), Ry(y) - матрицы собственных векторов; X, Y - произвольные матрицы.

Если сингулярные пучки D(x), D(y) имеют регулярные части Df(x), Df(y) соответственно, то последние и определяют пары конечных собственных значений. Если пучки не содержат регулярных частей, то формируется вспомогательная СНАУ (ВСНАУ) путем приравнивания полиномиальных решений пучка D(x) полиномиальным решениям пучка D(y).

 

Наверх

2.1. Спектральный метод решения СНАУ

Возможность построения пучков прямоугольных матриц обусловлена алгебраической структурой нуль-пространства матрицы СНАУ, представленного в специальном базисе. 

В качестве такого базиса для СНАУ от n переменных используется произведение Кронекера n векторов алгебраической структуры. Вектор алгебраической структуры xi для переменной xi - это вектор-столбец всех степеней данной переменной, начиная с нулевой, т.е.

. (2.2)

Его размер равен li? 1, причем li = si + 1. Для удобства записи вектор записывается в виде строки с указанием символа транспонирования [ ]T.

Тогда исходная СНАУ, включающая p уравнений с n неизвестными, может быть записана в следующем обобщенном виде

, . (2.3)

Используемый здесь базис [x1 x2 … xn] алгебраической структуры соответствует лексикографическому упорядочению переменных при использовании базиса Грёбнера.

Построение систем спектральных задач. Рассмотрим построение спектральных задач и ССЗ для системы нелинейных алгебраических уравнений (2.3) на примере СНАУ от одной и двух переменных. 

Решение нелинейного алгебраического уравнения. Пусть задано нелинейное алгебраическое уравнение вида

A1x n+1 xn+1 = 0, (2.4)

где A = [a0 a1 ... an]; xn+1 = [xn xn-1 ... x 1]T.

Введем вектор v = [xn-1 ... x 1]T, тогда вектор xn+1 может быть записан в виде [xv 1]T. Пусть Q0 = Ker(A); размер Q0равен (n + 1) x n.

Запишем Q0 в виде блочной матрицы Q0 = [q1 q2 ... qn qn+1]B, где qi (i = 1 ... n+1) - векторы-строки; ( )B - символ блочного транспонирования.

Введем векторы ax = [q1 q2 ... qn]B и bx = [q2 ... qn qn+1]B, составленные соответственно из n верхних и нижних строк матрицы Q0. Сопоставим вектору bx вектор v; тогда нетрудно убедиться, что ax = x bx, откуда следует следующая спектральная задача для определения неизвестной x:

(ax - x bx)r = 0, (2.5)

где ax, bx - квадратные матрицы размера n x n; r - собственный вектор пучка D(x), соответствующий собственному значению x. 

Решение СНАУ от одной переменной. СНАУ от одной переменной записываются следующим образом

Ap x n+1 Xn+1 = 0, (2.6)

где p - число уравнений.

Решение системы может быть сведено к спектральной задаче для следующего линейного пучка прямоугольных матриц

(ax - x bx) r = 0, (2.7)

где ax, bx - прямоугольные матрицы размера n x (n+1-rank(A)); 

r - собственный вектор пучка D(x) = ax - x bx, соответствующий собственному значению x. 

Решение СНАУ от двух переменных. Существует две эквивалентные формы для описания СНАУ от двух переменных

Ax [x A y] = 0; (2.8a) 

Ay [y A x] = 0, (2.8b)

где x, y -векторы алгебраической структуры, т.е.

x = [ ... x 1]T размера lx x 1, lx = sx+1;

y = [ ... y 1]T размера ly x 1, ly = sy+1;

Ax, Ay - постоянные матрицы размера p x (lx x ly); p - число уравнений.

СНАУ от двух переменных может быть сведена к следующей системе спектральных задач

; (2.9а)

; (2.9б)

(2.9в)

Если пучки имеют регулярные решения, то матрицы собственных векторов постоянны и не зависят от переменных x и y. В этом случае решения {xi } и {yi } являются собственными значениями регулярных блоков Df(x) и Df(y) пучков D(x) и D(y), соответственно.

Если пучки не имеют регулярных решений, то решения СНАУ могут быть получены из полиномиальных решений пучков D(x), D(y); в этом случае матрицы собственных векторов являются матричными полиномами и могут быть описаны в следующем виде

Rx(x) = Sl x l x; (2.10а)

Ry(y) = S l y l y, (2.10б)

где l x = [xt xt-1 ... x 1]T размера (t +1) x 1; l y = [yv yv-1 ... y 1]T размера (v+1) x 1.

Подставляя (2.10) в уравнение (2.9в), получим следующую вспомогательную СНАУ

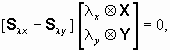(2.11)

где векторы и матрицы имеют размеры

size l x = [t+1 1]; size l y = [v+1 1];

size X = [m x 1]; size Y = [m y 1];

size Sl x = [N-p m x* (t+1)]; size Sl y = [N-p m y* (v+1)];

size[Sl x -Sl y] = [N-p Nl], N l = m x*(t+1)+m y*(v+1).

Матрицы Slx и Sly могут быть вычислены в соответствии с определением полиномиального решения, данного в работе [5].

Примем во внимание, что полиномиальные решения степеней t и v удовлетворяют матричным уравнениям

; 

, (2.12)

где

; ;

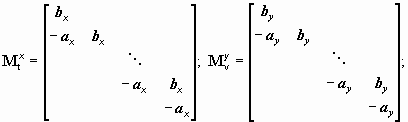
size Dx = [mx nx]; size Dy = [my ny];

size = [(t+2)mx (t+1)nx]; size = [(v+2)my (v+1)ny];

size = [(t+1)mx m x]; size = [(v+1)my m y];

m x = dim Ker(); m y = dim Ker().

Тогда справедливы соотношения

Sl x == ()B;

S ly = = ()B.

Построим для вспомогательной СНАУ (2.11) собственную ССЗ; для этого рассмотрим матрицу

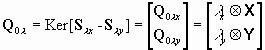 (2.13)

размера Nl x pl, где pl - число уравнений системы (2.11). Учитывая алгебраическую структуру векторов l x, l y, построим следующую ССЗ

(a lx - lx b lx) R lx = 0;

(a ly - ly b ly) R ly = 0, (2.14)

где D lx = a lx -lx b lx - пучок матриц размера mx t x Nl - pl;

D ly = a ly - ly b ly - пучок матриц размера my v x Nl - pl.

Возможные решения СНАУ порождаются регулярными блоками Df lx, Df ly пучков D lx, D ly соответственно. Если регулярные блоки для обоих классов решений (регулярного и полиномиального) не порождают возможных решений, то исходная СНАУ либо имеет бесчисленное множество решений, либо является приводимой, т.е. сводима к СНАУ от одной переменной с использованием базиса Гребнера [8, 9].

 

Наверх

2.2. Алгоритм решения СНАУ

Рассмотрим подробно алгоритм решения систем нелинейных алгебраических уравнений (СНАУ) от двух переменных вида: 

Ap*N [x  y] = 0, (2.15)

где Ap*N - матрица коэффициентов системы уравнений; 

x, y - векторы алгебраической структуры вида x = [xs...xj ...x 1]T, s = max j, ri = si +1; 

XN - кронекеровское произведение векторов xA y.

Алгебраическая структура вектора Xk позволяет свести задачу определения решения относительно переменных 

x1 .... xk к спектральной задаче для системы линейных сингулярных пучков вида [1, 3]

D(x1) r = ( a1 - x1 b1 ) r = 0; 

. . . . . . . . . . . . (2.16)

D(xk) r = ( ak - xk bk ) r = 0, 

где матрицы ai и bi имеют размеры (N si /ri) * (N - p), когда ранг матрицы Ap*N равен p.

Обратимся к анализу алгоритма решения СНАУ; основные блоки алгоритма показаны на рис. 1 ниже. 

Блок 1 выводит на экран параметры исходной СНАУ: матрицу системы, структуру вектора xA y, количество уравнений системы и максимальные степени переменных. В этом же блоке вычисляется нуль-пространства 

Q0x = Ker(Axy) и Q0y = Ker(Ayx) размера N x (N-p). 

Блок 1. Описание исходной СНАУ. Построение системы спектральных задач.
1.1.	Параметры исходной СНАУ
1.2.	Построение пучков D(x), D(y)
Блок 2. Вычисление структуры Кронекера
2.1.	Характеристики структуры Кронекера
2.2.	Структура Кронекера
2.3	Возможные источники решений
Блок 3. Вычисление решений системы спектральных задач (ССЗ)
3.1.	Формирование Mtx, Mvy
3.2.	Формирование вспомогательной СНАУ (ВСНАУ)
3.3.	Редукция числа уравнений ВСНАУ
3.4.	Формирование Qolx, Dlx, Qoly, Dly
3.5.	Выделение регулярной части Df lx, Df ly
Блок 4. Формирование решений ССЗ
4.1.	Вычисление спектра регулярных пучков
4.2.	Решения ССЗ
Блок 5. Определение допустимых пар решений ССЗ
5.1.	Редукция к СНАУ от одной переменной
5.2.	Формирование допустимых конечных пар решений
Блок 6. Формирование решений СНАУ
6.1.	Подстановка допустимых решений в исходную СНАУ и оценка точности
6.2.	Построение графика решений

Рис. 1. Схема алгоритма решения СНАУ

Для вычисления Q0y по известной матрице Q0x используется матрица перестановок P, связывающая векторы y  x и 

x  y, а следовательно, и соответствующие матрицы Q0y = PQ0x. Используя структуру вектора x  y, формируются пучки D(x) = ax - x bx и D(y) = = ay - y by.

Они позволяют составить систему уравнений 

(ax - x bx ) Rx = 0;

(ay - y by) Ry = 0. (2.17)

Базисным алгоритмом вычисления нуль-пространств является алгоритм SVD-разложения прямоугольной матрицы [10, 11]. 

Блок 2 вычисляет структуру Кронекера пучков D(x) и D(y). Структура Кронекера сингулярного пучка D(l ) = a - l bопределяется следующим образом [5-7]. Сингулярный пучок D(l ) размера m x n строго эквивалентен канонической форме Кронекера, если существуют постоянные невырожденные матрицы P Сmx m и Q Сnx n такие, что справедливо [6]

P(a - l b)Q = diag{Dr , Di , Df , Dl }, (2.18)

где Dr - сингулярная часть пучка, объединяющая блоки LtT размера t x (t+1); Di - регулярная часть пучка, соответствующая бесконечным собственным значениям; Df- регулярная часть пучка, соответствующая конечным собственным значениям; Dl - сингулярная часть пучка, объединяющая блоки Ls размера (s+1) x s.

Для того чтобы охарактеризовать структуры сингулярных блоков Dl и Dr , а также регулярных блоков Di и Df введем в рассмотрение следующие мультииндексы

a l = { l0 ... ls ... lu }; (2.19а)

a r = { r0 ... rt ... rw}; (2.19б)

a i = { ji1 ... jik ... jiv }; (2.19в)

a f = { jf1 ... jfk ... jfv }, (2.19г)

т.е. a l - мультииндекс, указывающий число блоков типа L0...Ls...Lu, соответствующих левым полиномиальным решениям; a r - мультииндекс, указывающий число блоков типа L0T...LtT...LwT, соответствующих правым полиномиальным решениям; a i - мультииндекс, указывающий число клеток Жордана Ji1...Jik...Jiv, соответствующих бесконечным собственным значениям; a f - мультииндекс, указывающий число клеток Жордана Jf1...Jfk...Jfv, соответствующих конечным собственным значениям с номерами f = {0, 1, ..., p}; u,v,w - индексы, задающие максимальные размеры сингулярных блоков и клеток Жордана.

Cледуя работе [6], введем мультииндекс

a = { a0 a1 ... af ... ap ai al ar }, (2.20)

который определяет структуру Кронекера сингулярного пучка прямоугольных матриц.

Число блоков Ls и LtT равно, соответственно

, , (2.21а)

а число клеток Жордана, соответствующих нулевым и бесконечным собственным значениям, равно, соответственно

, , (2.21б)

Следует отметить, что общее количество блоков разного типа, характеризующих структуру пучка, может быть вычислено на основе следующих соотношений

Nl = m - rank( [a b] ); (2.22а)

Nr = n - rank( [aH bH] ); (2.22б)

N0 = m - rank( a ); (2.22в)

Ni = m - rank( b ). (2.22г)

Эти соотношения не определяют состава блоков каждого типа, но дают общую интегральную оценку числа клеток Жордана с нулевыми (N0) и бесконечными собственными значениями (Ni ), общее количество правых (Nr) полиномиальных блоков LtT и левых (Nl) блоков Ls.

Выявление структуры мультииндексов ar (2.19б) и ai (2.19в) реализовано с помощью алгоритма RGSVD-разложения, который включен в ППП SNAE в виде М-функции sstruct на языке Matlab и обращение к которому имеет вид

[bk, ak, n(k), m(k)] = sstruct(b, a). (2.23)

Входные параметры: a, b - матрицы пучка a - l b .

Выходные параметры: n(k), m(k) - информационные векторы, описывающие структуру мультииндексов ar и ai; ak, bk - матрицы, полученные после одного шага RGSVD-алгоритма.

На основе информационных векторов n(k), m(k) можно сформировать следующую таблицу

Таблица

k	nk	mk	r0	r1	r2	r3	ji1	ji2	ji3
1	n1	m1	0	m1-n2
2	n2	m2	n2-m2	m2-n3
3	n3	m3	n3-m3	m3-n4
4	n4	0	n4

Она справедлива при следующих условиях, практически всегда имеющих место при анализе пучков, возникающих при решении СНАУ от двух переменных

n1= m1= Ni + Nr . (2.24)

Далее нетрудно убедиться, что выполняются соотношения 

Nr = (n2+n3+n4) - (m2+m3), Ni = (m1+m2+m3) - (n2+n3+n4), 

что подтверждает условие (2.24). Из таблицы следует, что мультииндексы могут быть записаны следующим образом

ar = {r0, r1, r2, r3} = { 0 n2-m2 n3-m3 n4 }; (2.25а)

ai = { ji1, ji2, ji3 } = { m1-n2 m2-n3 m3-n4 }. (2.25б)

Регулярная часть пучка Df = af - l bf определяется квадратными матрицами af и bf размера

size(Df) = [nf mf] = [n - m - ]. (2.26)

Размер пучка nf = mf отличен от нуля, когда процедура завершается по одному из условий: 

либо nk = 0, либо mk = 0 и < m.

Результатами работы блока 2 являются регулярные пучки Df (x) и Df (y), мультииндексы ar(x) и ar(y), а также список возможных источников решений. 

Блок 3 определяет решения системы спектральных задач, которые включают регулярные и полиномиальные решения.

Полиномиальное решение для пучка D(l ) = a - l b определяется следующим образом [5]. Векторный полином вида

x(l ) = stl t + st-1l t-1 + ... +s1l + s0 , (2.27)

где st, st-1, ... s1, s0 - векторы размера n x 1, является правым полиномиальным решением пучка, если при любом lвыполняется тождество (a - lb) x(l )  0, из которого следует справедливость соотношений

bst = 0; bst-1 = ast; ... bs0 = as1; as0 = 0 . (2.28)

Рассматривая эту систему равенств как систему линейных однородных уравнений относительно элементов столбцов 

st, st-1 ... s1, s0 можно сформировать систему вида

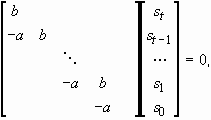(2.29а)

Уравнение (2.29a) может быть записано в следующем виде

Mt St = 0 , (2.29б)

где Mt - матрица коэффициентов уравнения (2.29а) размера [(t+2)*N*s1/r1 (t+1)*(N-p)]; St - ядро Ker(Mt) размера [(t+1)*(N-p) m ], m = dim Ker(Mt).

Введем в рассмотрение блочно транспонированную матрицу 

Sl = StB вида Sl =[St St-1...Sj...S1 S0], где size(Sj) = [N-p m ] для всех j от 1 до t. 

Для полиномиальных решений должно выполняться условие rx = ry, которое с учетом соотношений (2.27 - 2.29) можно записать в следующем виде 

S lx lx X = S ly ly Y, (2.30)

где S lx=(Stx)B, Stx = Ker(Mtx), m t = dim Ker(Mtx), mx = m t/rt;

S ly=(Svy)B, Svy = Ker(Mvy), m v = dim Ker(Mvy), my = m v/rv;

lx=[xt ... 1]T, ly=[yv ... 1]T; 

X - вектор размера [mx 1]; Y - вектор размера [my 1].

Число таких уравнений равно произведению величин Nrx и Nr y, вычисленных по соотношению (2.22б).

Cоотношения (2.28 - 2.30) определяют следующую последовательность шагов алгоритма в блоке 3:

Шаг 3.1. Формирование матрицы Mtx и Mvy с учетом структуры мультииндексов arx и ar y по переменным x и y.

Шаг 3.2. Формирование вспомогательной СНАУ. Для этого вычисляются нуль-пространства 

Stx = Ker(Mtx) и Svy = Ker(Mvy) и по каждой переменной строится мультииндекс m , объединяющий размерности ядер 

m t = dim Ker(Mt), зависящие от t 

m = [ m 0 m 1 ... m t ... mw ], (2.31)

который можно сопоставить с мультииндексом ar (2.19б). Так например, структура мультииндекса дефектов матрицы Mt, соответствующая мультииндексу (2.25а) структуры правых полиномиальных решений, вычисленных в блоке 2, должна иметь вид

m = [ 0 m 1 m 2 m 3 ]. (2.31а)

Сформировать системы уравнений вида 

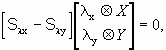(2.32)

где векторы и матрицы имеют следующие размеры

size l x = [t+1 1]; size l y = [v+1 1];

size X = [mx 1]; size Y = [my 1];

size S lx = [N-p mx* (t+1)]; size S ly = [N-p my* (v+1)];

size[S lx -S ly ] = [N-p mx*(t+1)+my *(v+1)].

Шаг 3.3. Редукция числа уравнений. Все отобранные уравнения удовлетворяют системе (2.32), причем число уравнений этой системы может быть уменьшено, если выполняются некоторые условия. Системе (2.32) соответствует пучок Dlxразмера [mx* t mx* (t+1)+my* (v+1)-pl], где pl - число уравнений системы. Условие регулярности пучка определяется соотношением

pl* = mx + my* (v+1) . (2.33)

Если оказывается, что текущее pl > pl*, то число уравнений, используемых для формирования СНАУ (2.32), следует сократить до величины pl*. Если описанная редукция возможна, то на следующем шаге pl = pl*, а сформированный пучок будет регулярным; если - нет, то число уравнений остается равным pl = N-p, а пучок - сингулярным.

Шаг 3.4. Вычисление 

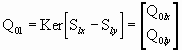(2.34)

размера [Nl Nl-pl], где Nl = mx*(t+1)+my*(v+1).

Выделить из матрицы Q0l подматрицу Q0l x, соответствующую подблоку l x  X и имеющую размер [mx*(t+1) Nl-pl]. Сформировать пучок Dlx = alx - xblx размера [m *t Nl-pl]. Если редукция на шаге 3.3 была успешной, то сформированный пучок - регулярный и можно переходить к блоку 4, не выполняя шаг 3.3. 

Шаг 3.5. Выделение из сингулярных пучков Dlx и Dly, полученных на шаге 3.4, регулярных частей 

Dflx = aflx-xbflx и 

Dfl y = afly - xbfl y.

Блок 4 формирует решения ССЗ. Вычислить спектры регулярных пучков Df(x) и Df(y), полученных в блоке 2 и Dflx и Dfly, полученных в блоке 3, используя процедуру eig(a, b) [12] решения обобщенной проблемы собственных значений. Результатом является множество решений {xi} и {yi} по переменным x и y.

Блок 5 определяет допустимых пар решений ССЗ. Этот блок использует следующую последовательность шагов.

Шаг 5.1. Каждое из вычисленных в блоке 4 решение подставляется в исходную СНАУ и таким образом выполняется редукция к СНАУ от одной переменной. Вычисляются решения этой СНАУ и формируются все допустимые пары решений, включая решения типа Inf и NaN. 

Шаг 5.2. Из найденных на шаге 5.2 пар решений извлекаются только конечные пары {xi, yi}.

Блок 6 формирует решения СНАУ. Этот блок включает два шага.

Шаг 6.1. Найденные конечные пары решений подставляются в исходную СНАУ и вычисляются невязки для каждого уравнения системы. Сумма модулей этих невязок служит оценкой точности решений СНАУ. 

Шаг 6.2. Построение графика решений, на который выводится графический образ исходной матрицы и множество всех значений {xi } и {yi }, как действительных, так и комплексных.

Из схемы алгоритма наглядно видно, что ряд блоков и шагов обладают естественным параллелизмом, обусловленным применением одной процедуры к различным данным.

Алгоритм решения СНАУ в полном объеме реализован в среде системы научных расчетов Matlab 5 [13].

В качестве теста рассмотрим пример решения системы нелинейных алгебраических уравнений от двух переменных вида

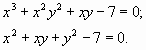
Протокол решения приведен ниже и не нуждается в дополнительных комментариях. Последовательность решения соответствует всем вышеописанным блокам алгоритма.

 

Наверх

2.3. Протокол решения тестовой системы

% ********************************************************

%

% Решение 

% систем нелинейных алгебраических уравнений (СНАУ)

% от двух переменных:

%

% Axy*[x**y] = 0, 

%

% ******************************************************** 

%

% Axy - матрица СНАУ размера p*N;

% N - число столбцов матрицы A, длина вектора x**y;

% x, y - векторы алгебраической структуры

% sx jx

% [ x*..*x ... x*..*x ... 1 ],

% sy jy

% [ y*..*y ... y*..*y ... 1 ]

% jx, jy - степени переменных x(jp, jx), y(jp, jy);

% sx, sy - максимальные степени переменных x, y;

% x**y - произведение Кронекера.

echo off

flagreal = 0

БЛОК 1. Описание СНАУ. Построение (ССЗ) 

Шаг 1.1. Параметры СНАУ 

Вы работаете со следующей СНАУ:

Axy =

0 0 1 1 0 0 0 1 0 0 0 -7

0 0 0 0 0 1 0 1 0 1 0 -7

ranka = 2

XN = [ xxxyy xxxy xxx xxyy xxy xx xyy xy x yy y 1 ]

Количество уравнений

p = 2

Максимальная степень переменной x

sx = 3

Максимальная степень переменной y

sy = 2

БЛОК 2. Вычисление структуры Кронекера 

Размеры пучков: D(x) D(y) 

9*10 8*10

Шаг 2.1. Характеристики структуры Кронекера 

Характеристики структуры Кронекера для D(x) 

[ Nl Nr N0 Ni ]

Nx = 0 1 0 1

Характеристики структуры Кронекера для D(y) 

[ Nl Nr N0 Ni ]

Ny = 0 2 0 0

Nl - число левых полиномиальных решений

Nr - число правых полиномиальных решений

N0 - число блоков Жордана с нулевыми собственными значениями

Ni - число блоков Жордана с бесконечными собственными значениями

Шаг 2.2. Структура Кронекера 

Структура Кронекера пучка D(x)

k nk mk r0 r1 r2 r3 r4 r5 r6 J1 J2 J3 J4 J5 J6

1 2 2 0 0 

2 2 2 0 1 

3 1 1 0 0 

4 1 1 0 0 

5 1 1 0 0 

6 1 1 0 0 

7 1 0 1 

Структура Кронекера пучка D(y)

k nk mk r0 r1 r2 r3 r4 J1 J2 J3 J4

1 2 2 0 0 

2 2 2 0 0 

3 2 2 0 0 

4 2 2 0 0 

5 2 0 2 

Шаг 2.3. Возможные источники решений

Решения по X:

************************************************

- регулярные решения [n n]:

nfx = 1

- полиномиальные решения:

alrx = 0 0 0 0 0 0 1

************************************************

Решения по Y:

************************************************

- регулярных решений нет :

nfy = 0

- полиномиальные решения:

alry = 0 0 0 0 2

************************************************

БЛОК 3. Нахождение полиномиальных решений

Шаг 3.1. Формирование Mt, Mv 

Характеристики Mt

s m n rnk mu alr

0 18 10 10 0 0

1 27 20 20 0 0

2 36 30 30 0 0

3 45 40 40 0 0

4 54 50 50 0 0

5 63 60 60 0 0

6 72 70 69 1 1

Характеристики Mv

s m n rnk mu alr

0 16 10 10 0 0

1 24 20 20 0 0

2 32 30 30 0 0

3 40 40 40 0 0

4 48 50 48 2 2

Шаг 3.2. Формирование вспомогательной СНАУ (ВСНАУ)

Характеристики ВСНАУ 

До редукции

Размер: Sl 

10*17

Шаг 3.3. Редукция уравнений ВСНАУ

Редукция по y

pl = 10 ----> ply = 9

После редукции:

Размер: Sl 

9*17

N0l pl plx ply 

ans = 10 10 11 9

N0l - число уравнений ВСНАУ

pl - ранг ВСНАУ

plx - число уравнений для формирования регулярных пучков по x

ply - число уравнений для формирования регулярных пучков по y

Шаг 3.4. Формирование q0lx, D0lx, q0ly, D0ly 

Размеры матриц: q0l(x) q0l(y) 

7*8 10*8

Размеры пучков: D0l(x) D0l(y) 

6*8 8*8

Ранги: 6 8

6 7

Характеристики структуры Кронекера для D0l(x) 

[ Nl Nr N0 Ni ]

Nlx = 0 2 0 0

Характеристики структуры Кронекера для D0l(y) 

[ Nl Nr N0 Ni ]

Nly = 0 0 0 1

Nl - число левых полиномиальных решений

Nr - число правых полиномиальных решений

N0 - число блоков Жордана с нулевыми собственными значениями

Ni - число блоков Жордана с бесконечными собственными значениями

Шаг 3.5. Формирование регулярных частей Dflx, Dfly 

Регулярные пучки для ВСНАУ

Размеры пучков: Dfl(x) Dfl(y) 

0*0 6*6

БЛОК 4. Формирование решений ССЗ 

Шаг 4.1. Вычисление собственных значений регулярных пучков 

Распределение решений по классам 

Dfx Dflx Dfy Dfly

ans = 1 0 0 6

Шаг 4.2. 

Решения ССЗ

x =

1.0000e+000

y =

3.0251e+000 

2.1154e+000 

2.6514e-001 - 1.4533e+000i

2.6514e-001 + 1.4533e+000i

-1.8354e+000 - 3.7391e-001i

-1.8354e+000 + 3.7391e-001i

БЛОК 5. Вычисление допустимых решений ССЗ 

Шаг 5.1. Редукция к СНАУ от одной переменной 

ДОПУСТИМЫЕ ПАРЫ РЕШЕНИЙ ССЗ 

x y

1.0000e+000 -3.0000e+000 

1.0000e+000 2.0000e+000 

-1.1427e+000 3.0251e+000 

-2.9666e+000 2.1154e+000 

2.7900e+000 + 8.2555e-001i 2.6514e-001 - 1.4533e+000i

2.7900e+000 - 8.2555e-001i 2.6514e-001 + 1.4533e+000i

-1.2353e+000 + 4.2601e-001i -1.8354e+000 - 3.7391e-001i

-1.2353e+000 - 4.2601e-001i -1.8354e+000 + 3.7391e-001i

Шаг 5.2. 

ДОПУСТИМЫЕ ПАРЫ КОНЕЧНЫХ РЕШЕНИЙ ССЗ 

x y

1.0000e+000 -3.0000e+000 

1.0000e+000 2.0000e+000 

-1.1427e+000 3.0251e+000 

-2.9666e+000 2.1154e+000 

2.7900e+000 + 8.2555e-001i 2.6514e-001 - 1.4533e+000i

2.7900e+000 - 8.2555e-001i 2.6514e-001 + 1.4533e+000i

-1.2353e+000 + 4.2601e-001i -1.8354e+000 - 3.7391e-001i

-1.2353e+000 - 4.2601e-001i -1.8354e+000 + 3.7391e-001i

БЛОК 6. Формирование решений СНАУ 

Шаг 6.1. Подстановка решений ССЗ в СНАУ и вычисление невязок

РЕШЕНИЯ СНАУ 

x y

1.0000e+000 -3.0000e+000 

1.0000e+000 2.0000e+000 

-1.1427e+000 3.0251e+000 

-2.9666e+000 2.1154e+000 

2.7900e+000 + 8.2555e-001i 2.6514e-001 - 1.4533e+000i

2.7900e+000 - 8.2555e-001i 2.6514e-001 + 1.4533e+000i

-1.2353e+000 + 4.2601e-001i -1.8354e+000 - 3.7391e-001i

-1.2353e+000 - 4.2601e-001i -1.8354e+000 + 3.7391e-001i

ТОЧНОСТЬ РЕШЕНИЯ 

reps = 3.8481e-013

Шаг 6.2: Графики исходной СНАУ и решений:

 

Наверх

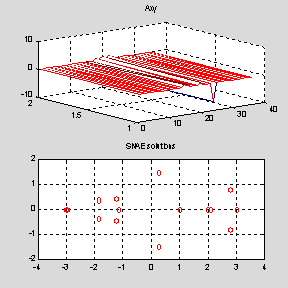
Список литературы

1. Кублановская В.Н. О связи спектральной задачи для линейных пучков матриц с некоторыми задачами алгебры. //Записки научных семинаров ЛОМИ "Численные методы и вопросы организации вычислений". 1978. T.80. C. 98-116.

2. Van Dooren P. The computation of Kronecker's canonical form of a singular pencil. //Lin. Alg. & Appl. 1979. Vol.27. P. 103-141. 

3. Потемкин В.Г. Алгоритм решения систем нелинейных алгебраических уравнений на основе разложения сингулярного пучка матриц. //Вестник Российской транспьютерной ассоциации. 1994. № 2(13). C. 5-18. 

4. Borisevich V.D., Potemkin V.G. Direct method for SNAE solving in modeling of gas flow in centrifuge. //Separation Phenomena in Liquids and Gases. Fourth Workshop procceedings. Ed. C. Ying. Tsinghua University. Beijing, 1994. P. 115-127.

5. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.: Наука, 1988. 552 c. 

6. Van Dooren P. Reducing subspaces: definition, principles and algorithms. P. 58-73. //In: Ka gstro m B., Ruhe A. Matrix pencils. Proceedings, Pite Havsbad, 1982, Lecture Notes in Mathematics 973. Berlin: Springer-Verlag, 1983. 293 p. 

7. Buchberger B. Gro bner Bases: An algorithmic method in polynomial ideal theory. //In: Multidimensional systems theory (Ed. N.K. Bose.). D. Reidel Publ. Comp., 1985. P. 184-232.

8. Ka gstro m B. RGSVD - An algorithm for computing the Kronecker structure and reducing subspaces of singular A-l B pencils. SIAM J. Sci. Stat. Comput. 1986. Vol.7. № 1. Jan. P. 185-211. 

9. Уфнаровский В.А. Комбинаторные и асимптотические методы алгебры. //Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. T.57. Алгебра 6. М.: ВИНИТИ, 1990. C. 7-177.

10. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра. /Пер. с англ. М.: Машиностроение, 1976. 389 c.

11. Golub G.H., van Loan C.F. Matrix computations. //North Oxford Academic Publishers Ltd. 1986. 474 p.

12. Потемкин В.Г. Система MATLAB. Справочное пособие. М.: ДИАЛОГ-МИФИ, 1997. 350 с.

13. Потемкин В.Г. MATLAB 5 для студентов. М.: ДИАЛОГ-МИФИ, 1998. 314 с.