Теоретический курс и примеры по курсу линейной алгебры
Теоретический курс и примеры по курсу линейной алгебры в среде MATLAB для студентов, изучающих высшую математику. Здесь собраны примеры решения типовых задач курса ЛА. Все примеры решены в среде математического пакета MATLAB доступны для просмотра.
Матрицы. Действия с матрицами
-
Пример 1. Действия с матрицами
-
Пример 2. Проверка перестановочности матриц
-
Пример 3. Умножение матрицы на матрицы специального вида
-
Пример 4. Возведение матрицы в степень
-
Пример 5. Обращение матрицы
-
Пример 6. Ортогональная матрица
Определители. Вычисление определителей
-
Пример 1. Вычисление определителя разложением по 1-ой строке
-
Пример 2. Вычисление определителей матриц 2 и 3 порядков
Методы решения систем линейных алгебраических уравнений
-
Пример 1. Решение матричного уравнения
-
Пример 2. Вычисление решения системы линейных уравнений по формулам Крамера
-
Пример 3. Решение системы линейных уравнений методом Гаусса
Общая теория систем линейных уравнений. Однородные системы
-
Пример 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей
-
Пример 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизестными
-
Пример 3. Исследование однородной системы на совместность методом Гаусса
Общая теория систем линейных уравнений. Неоднородные системы
-
Пример 1. Проверка условия совместности неоднородной системы
-
Пример 2. Исследование неоднородной системы для двух различных правых частей методом Гаусса
Теоретическая справка
1. Матрицы. Действия с матрицами
2. Определители. Вычисление определителей
3. Методы решения систем линейных алгебраических уравнений
4. Общая теория систем линейных уравнений. Однородные системы
5. Общая теория систем линейных уравнений. Неоднородные системы
6. Линейное пространство. Основные понятия
7. Элементарная теория линейных операторов
Примеры по теме "Матрицы. Действия с матрицами" курса ЛА
Пример 1. Действия с матрицами
Вычислим матрицу 2A-BA, где  и
и  .
.
Решение примера в среде MATLAB:
% Введём матрицы A и B
A = [2 3; 1 0; -1 3];
B = [2 0 1; 1 -2 2; 5 0 7];
% Вычислим 2A - BA
C = 2*A - B*A;
% Выведем результат
disp(C);
| >> | 1 | -3 |
| 4 | -9 | |
| -5 | -30 |
Пример 2. Проверка перестановочности матриц
Проверим, что матрицы 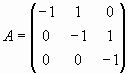 и
и 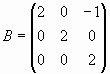 перестановочны, а матрицы А и
перестановочны, а матрицы А и  неперестановочны.
неперестановочны.
Решение примера в среде MATLAB:
% Введём матрицы A и B
A = [-1 1 0; 0 -1 1; 0 0 -1];
B = [2 0 -1; 0 2 0; 0 0 2];
% Проверим AB == BA
same(A*B,B*A) % Выведет 2 - да, 0 - нет. Проверка на идентичность.
% Введём матрицу С
C = [2 8 3; 3 0 -2; 7 2 1];
% Проверим AC == CA
same(A*C,C*A) % Выведет 2 - да, 0 - нет.
>>
ans = 2
ans = 0
Пример 3. Умножение матрицы на матрицы специального вида
Умножим матрицу 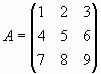 на единичную, скалярную и матрицы
на единичную, скалярную и матрицы 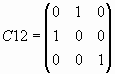 и
и 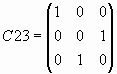 .
.
Решение примера в среде MATLAB:
% Введём матрицу A
A = [1 2 3; 4 5 6; 7 8 9];
% Введём перестановочные матрицы
C12 = [0 1 0; 1 0 0; 0 0 1];
C23 = [1 0 0; 0 0 1; 0 1 0];
% Проверим результат
C12 * A % Перестановка строк
C23 * A % Перестановка строк
A * C12 % Перестановка столбцов
A * C23 % Перестановка столбцов
% Как это сделать средствами MATLAB
A([2 1 3], :) % Перестановка строк
A([1 3 2], :) % Перестановка строк
A(:, [2 1 3]) % Перестановка столбцов
A(:, [1 3 2]) % Перестановка столбцов
>>
| ans = | 4 | 5 | 6 |
| 1 | 2 | 3 | |
| 7 | 8 | 9 |
| ans = | 1 | 2 | 3 |
| 7 | 8 | 9 | |
| 4 | 5 | 6 |
Пример 4. Возведение матрицы в степень
Для матрицы ![]() найдем A0, A1, A2.
найдем A0, A1, A2.
Решение примера в среде MATLAB:
% Введём матрицу A
A = [2 -1; 3 1];
% Вычислим A^0, A^1, A^2 и выведем результат
A^0, A^1, A^2
>>
| ans = | 1 | 0 |
| 0 | 1 |
| ans = | 2 | -1 |
| 3 | 1 |
| ans = | 1 | -3 |
| 9 | -2 |
Пример 5. Обращение матрицы
Проверим, что матрица 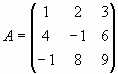 невырождена и найдем матрицу A-1.
невырождена и найдем матрицу A-1.
Решение примера в среде MATLAB:
% Введём исходную матрицу
A=[1 2 3; 4 -1 6; -1 8 9];
% Вычислим к ней обратную. Выведем результат.
inv(A)
ans =
| 1.1875 | -0.1250 | -0.3125 |
| 0.8750 | -0.2500 | -0.1250 |
| 0.6458 | - 0.2083 | 0.1875 |
Пример 6. Ортогональная матрица
Проверим, что матрица ![]() ортогональна.
ортогональна.
Решение примера в среде MATLAB:
% Вычислим матрицу поворота на угол alpha. Будем использовать символьную математику
syms alpha;
U = [cos(alpha) sin(alpha); -sin(alpha) cos(alpha)];
% Условие ортогональности U * U' = E
simplify(U*U.')
% Знак .' означает транспонирование, тогда как ' - сопряжение
% conj(U.') = U', где conj - комплексное сопряжение.
>>
| ans = | [ 1, 0] |
| [ 0, 1] |
Примеры по теме "Определители. Вычисление определителей" курса ЛА
Пример 1. Вычисление определителя матрицы разложением по 1-ой строке
Вычислим определитель матрицы четвертого порядка разложением по 1-ой строке
Решение примера в среде MATLAB:
% Введём матрицу A
A = [1 -2 3 0; 2 3 0 1; -7 5 6 7; 3 10 12 13];
% Вычислим определитель разложением по первой строке
detA1 = 1 * acomp(A,1,1) - 2 * acomp(A,1,2) + 3 * acomp(A,1,3)
% Вычислим определитель с помощью встроенной функции
detA2 = det(A)
>>
detA1 = 477
detA2 = 477
Пример 2. Вычисление определителей матриц 2 и 3 порядков
Вычислим определители матриц ![]() и
и  .
.
Решение примера в среде MATLAB:
% Получим аналитическое представление для определителей порядка 2 и 3.
% Все переменные - символьные
syms a11 a12 a13 a21 a22 a23 a31 a32 a33;
% Введём матрицы
A2 = [a11 a12; a21 a22];
A3 = [a11 a12 a13; a21 a22 a23; a31 a32 a33];
% Формулы для определителей
det(A2)
det(A3)
>>
ans = a11*a22-a12*a21
ans = a11*a22*a33-a11*a23*a32-a21*a12*a33+a21*a13*a32+a31*a12*a23-a31*a13*a22
Примеры по теме "Методы решения систем линейных алгебраических уравнений" курса ЛА
Пример 1. Решение матричного уравнения
Запишем систему в матричном виде и решим матричное уравнение.
Решение примера в среде MATLAB:
% Перепишем систему в векторном виде и введём её матрицы
A = [1 2 3; 1 -3 2; 1 1 1];
b = [7;5;3];
% Решаем систему Ax=b
% Проверим систему на невырожденность
rank(A)
>> ans = 3
% Ранг системы полный, система невырождена
% Решим систему с помощью обратной матрицы. x=A^(-1)*b
x = inv(A) * b
| >> | x = | 1.0000 |
| 0 | ||
| 2.0000 |
% Решим систему с помощью средств MATLAB для решения линейных систем
x = A \ b
| >> | x = | 1 |
| 0 | ||
| 2 |
Пример 2. Вычисление решения системы линейных уравнений по формулам Крамера
Найти по формулам Крамера решение системы линейных уравнений 
Решение примера в среде MATLAB:
% Решим систему методом Крамера
A = [1 2 3 4; -1 2 -3 4; 0 1 -1 1; 1 1 1 1];
b = [30;10;3;10];
% Проверим невырожденность системы
rank(A)
>> ans = 4
% По правилу Крамера
A1 = A;
A2 = A;
A3 = A;
A4 = A;
A1(:,1) = b;
A2(:,2) = b;
A3(:,3) = b;
A4(:,4) = b;
x1 = det(A1) / det(A);
x2 = det(A2) / det(A);
x3 = det(A3) / det(A);
x4 = det(A4) / det(A);
x=[x1;x2;x3;x4];
% Проверим решение
A*x - b
| >> | ans = | 0 |
| 0 | ||
| 0 | ||
| 0 |
Пример 3. Решение системы линейных уравнений методом Гаусса
Решение примера в среде MATLAB:
% Решим систему Ax=b методом Гаусса.
% Для этого, сформируем расширенную систему
A = [1 2 3; 1 -3 2; 1 1 1];
b = [7;5;3];
C = [A b];
% Приведём её к ступенчатому виду, выполнив прямой и обратный ход метода Гаусса
D = rref(C)
| >> | D = | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 2 |
% Последний столбец матрицы есть решение
x = D(:,4);
% Проверим его
A*x - b
| >> | ans = | 0 |
| 0 | ||
| 0 |
Примеры по теме "Общая теория систем линейных алгебраических уравнений. Однородные системы" курса ЛА
Пример 1. Нетривиальная совместность системы линейных уравнений с квадратной матрицей
Проверим условие нетривиальной совместности однородной системы 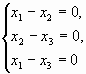 с квадратной матрицей
с квадратной матрицей 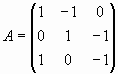 .
.
Решение примера в среде MATLAB:
% Введём матрицу A
A = [1 -1 0; 0 1 -1; 1 0 -1];
% Условие нетривиальности системы Ax=0 - вырожденность A.
% Проверим определитель A == 0, тогда система имеет нетривиальные решения
det(A)
>> ans = 0
Пример 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизвестными
Проверим условие нетривиальной совместности однородной системы 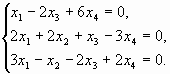
Решение примера в среде MATLAB:
% Проверим на нетривиальну разрешимость систему с неквадратной матрицей A
A = [1 0 -2 6; 2 2 1 -3; 3 -1 -2 2];
% Для этого достаточно rank(A) < 4
rank(A)
>> ans = 3
Пример 3. Исследование однородной системы на совместность методом Гаусса
Исследуем однородную систему 
Решение примера в среде MATLAB:
% Определим систему на нетривиальность методом Гаусса.
A = [1 4 2 0 -3; 2 9 5 2 1; 1 3 1 -2 -9; 3 12 6 0 -8; 2 10 6 4 7];
% Приведём матрицу к ступенчатому виду
C = rref(A)
| >> | C = | 1 | 0 | -2 | -8 | 0 |
| 0 | 1 | 1 | 2 | 0 | ||
| 0 | 0 | 0 | 0 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 |
% Видим, что размерность линейного пространства Ax=0 равна 2.
% В качестве свободных переменных выберем x1, x2.
% Тогда, решая неоднородную систему
C = C(1:3,3:end);
syms x1 x2;
D = [C [x1;x2;0]];
E = rref(D)
| >> | E = | [ 1, | 0, | 0, | 1/2*x1+2*x2] |
| [ 0, | 1, | 0, | -1/2*x2-1/4*x1] | ||
| [ 0, | 0, | 1, | 0] |
% Тогда, решением будет
E(:,end)
% где x1,x2 - свободные переменные
| >> | ans = | [ 1/2*x1+2*x2] |
| [ -1/2*x2-1/4*x1] | ||
| [ 0] |
% Найдём базис ядра оператора A - фундаментальную систему решений Ax=0
null(A)
| >> | ans = | -0.4439 | -0.8581 |
| 0.4828 | -0.0167 | ||
| -0.7436 | 0.4624 | ||
| 0.1304 | -0.2229 | ||
| -0.0000 | -0.0000 |
Примеры по теме "Общая теория систем линейных алгебраических уравнений. Неоднородные системы" курса ЛА
Пример 1. Проверка условия совместности неоднородной системы
Проверим условие совместности неоднородной системы 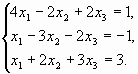
Решение примера в среде MATLAB:
% Рассмотрим систему Ax=b
A = [4 -2 2; 1 -3 -2; 1 2 3];
b = [1;-1;3];
% Сравним ранги исходной и расширенной матриц
rank(A)
rank([A b])
| >> | ans = 2 |
| ans = 3 |
% Ранг расширенной матрицы больше, значит система несовместна.
Пример 2. Исследование неоднородной системы для двух различных правых частей методом Гаусса
Исследуем неоднородную систему линейных уравнений Ax=b для двух различных правых частей b=b1 и b=b2.
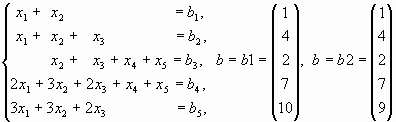 .
.
Решение примера в среде MATLAB:
% Исследуем систему Ax=b1 и Ax=b2 методом Гаусса
A = [1 1 0 0 0; 1 1 1 0 0; 0 1 1 1 1; 2 3 2 1 1;3 3 2 0 0];
b1 = [1;4;2;7;10];
b2 = [1;4;2;7;9];
% Приведём матрицы к ступенчатому виду
A1 = rref([A b1])
% Эта система оказывается несовместна
| >> | A1 = | 1 | 0 | 0 | -1 | -1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
% Видно, что система Ax=b2 совместна
A2 = rref([A b2])
| >> | A2 = | 1 | 0 | 0 | -1 | -1 | 2 |
| 0 | 1 | 0 | 1 | 1 | -1 | ||
| 0 | 0 | 1 | 0 | 0 | 3 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
% Найдя базис ядра оператора A
null(sym(A))
| >> | ans = | [ -1, 0] |
| [ 1, 0] | ||
| [ 0, 0] | ||
| [ 0, 1] | ||
| [ -1, -1] |
% и зная частное решение
sym(A)\sym(b2)
% мы легко получаем общее решение
| >> | ans = | [ 2] |
| [ -1] | ||
| [ 3] | ||
| [ 0] | ||
| [ 0] |
1. Матрицы. Действия с матрицами
Матрицей размерности m x n называется прямоугольная таблица m x n чисел a ij , i=1,..., m, j=1,..., n:
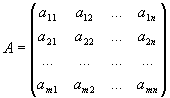
расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).
Линейные матричные операции
По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.
Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.
Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если
.gif) ,
,  ,
,
то произведением матриц A и B, называется матрица
 ,
,
элементы которой вычисляются по формуле
c ij =a i1 b 1j + a i2 b 2j + ... +a in b nj , i=1, ..., m, j=1, ..., k.
Произведение матриц A и B обозначается AB, т.е. C=AB.
Произведение матриц, вообще говоря, зависит от порядка сомножителей. Если AB=BA, то матрицы A и B называются перестановочными.
Для квадратных матриц определена единичная матрица - квадратная матрица, все диагональные элементы которой единицы, а остальные - нули:
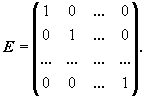
Единичная матрица чаще всего обозначается буквой E или E n, где n - порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы:
AE=EA=A.
Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица - частный случай скалярной матрицы.
Для квадратных матриц определена операция возведения в целую неотрицательную степень:
A 0 =E, A 1 =A, A 2 =AA, ..., A n =A n-1 A, ....
Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу A. Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A T:
.gif) ,
, 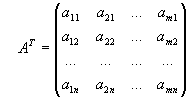 .
.
Верны соотношения:
(AT )T =A;
(A+B)T=AT +BT ;
(AB)T =BT AT.
Квадратная матрица A, для которой A T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.
Квадратная матрица A называется обратимой, если существует такая матрица X, что
AX=XA=E.
Матрица X называется обратной к матрице A и обозначается A -1, т.е.
A A -1 =A -1A=E.
Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A -1.
Верно соотношение: (A-1)T =(AT ) -1.
Квадратная матрица U, для которой U -1 =U T, называется ортогональной матрицей.
Свойства ортогональной матрицы:
-
Модуль определителя ортогональной матрицы равен единице.
-
Сумма квадратов элементов любого столбца ортогональной матрицы равна единице.
-
Сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна нулю. Такими же свойствами обладают строки ортогональной матрицы.
2. Определители. Вычисление определителей
Пусть A квадратная матрица порядка n, n>1. Определителем квадратной матрицы A порядка n называется число
det A=  =
= 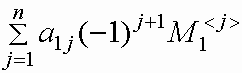 ,
,
где M1 <j> - определитель квадратной матрицы порядка n -1, полученной из матрицы A вычеркиванием первой строки и j -го столбца, называемый минором элемента a1j .
Формула
det A = .gif)
называется формулой вычисления определителя разложением по первой строке.
Число (-1) j+1 M1 <j> называется алгебраическим дополнением элемента a1j.
Пусть Mi <j> - определитель квадратной матрицы порядка n-1, полученной из матрицы A вычеркиванием i-й строки и j-го столбца (минор элемента aij ).
Число (-1) j+i Mi <j> называется алгебраическим дополнением элемента aij матрицы A.
Справедливы формулы вычисления определителя квадратной матрицы A разложением по i-й строке и разложением по j-му столбцу:
det A= .gif) =
= 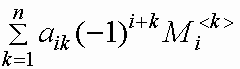 =
=
= 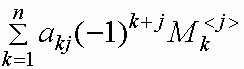
для i=1,2,...,n, j=1,2,...,n.
Для квадратной матрицы второго порядка формула вычисления определителя упрощается:
det 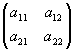 =
= 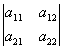 = a11 a22 - a12 a21,
= a11 a22 - a12 a21,
поскольку, например, в формуле разложения определителя по 1-ой строке
M1 < 1> =a22 , M1 < 2> =a21.
Для квадратной матрицы третьего порядка формула вычисления определителя разложением по 1-ой строке имеет вид:
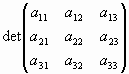 =
=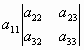 -
-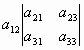 +
+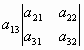 .
.
3. Методы решения систем линейных алгебраических уравнений
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x1 , x2 , ..., xn:
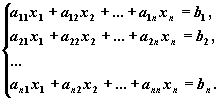
Эта система в "свернутом" виде может быть записана так:
S ni=1aij xj = bi , i=1,2, ..., n.
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где
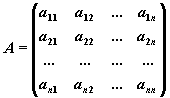 ,
, 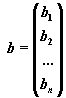 ,
, 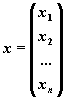 .
.
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.
Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.
Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой:
x=A -1 b.
Справедливо следующее утверждение (формулы Крамера).
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1 , x2 , ..., xn, определяемое формулами Крамера
xi =Di / D, i=1,2, ..., n,
где Di - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn
.gif)
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
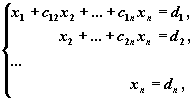
решение которой находят по рекуррентным формулам:
xn =dn , xi = di -S nk=i+1 cik xk , i=n-1, n-2, ...,1.
Матричная запись метода Гаусса.
-
Прямой ход метода Гаусса: приведение расширенной матрицы системы
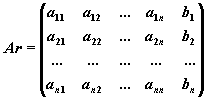
к ступенчатому виду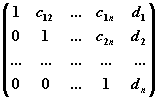
с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:-
перестановка строк;
-
умножение строки на число, отличное от нуля;
-
сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).
-
-
Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
 ,
,
последний, (n+1)-й, столбец этой матрицы содержит решение системы.
4. Общая теория систем линейных уравнений. Однородные системы
Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных
x1 , x2 , ..., xn :
.gif)
Решением системы называется совокупность n значений неизвестных
x1=x'1 , x2 =x'2 , ..., xn=x'n ,
при подстановке которых все уравнения системы обращаются в тождества.
Система линейных уравнений может быть записана в матричном виде:
![]()
где A — матрица системы, b — правая часть, x — искомое решение, Ap — расширенная матрица системы:
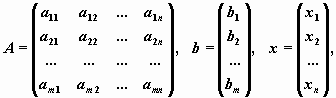
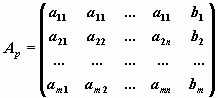 .
.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Однородной системой линейных уравнений называется система, правая часть которой равна нулю:
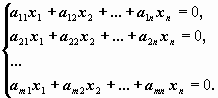
Матричный вид однородной системы: Ax=0.
Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:
x1=0 , x2=0 , ..., xn=0.
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.
Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду
 .
.
Число r ненулевых строк в ступенчатой форме матрицы называется рангом матрицы, обозначаем
r=rg(A) или r=Rg(A).
Справедливо следующее утверждение.
Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы рангr матрицы системы был меньше числа неизвестных n.
Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.
Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-rлинейно независимых решений.
Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0 меньше числа неизвестных n и векторы
e1 , e2 , ..., en-r образуют ее фундаментальную систему решений (Aei =0, i=1,2, ..., n-r), то любое решение xсистемы Ax=0 можно записать в виде
x=c1 e1 + c2 e2 + ... + cn-r en-r ,
где c1 , c2 , ..., cn-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.
Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.
Исследуем однородную систему методом Гаусса.
Пусть
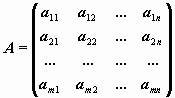
матрица исследуемой однородной системы, ранг которой r< n.
Такая матрица приводится Гауссовым исключением к ступенчатому виду
 .
.
Соответствующая эквивалентная система имеет вид
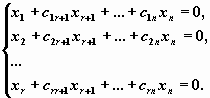
Отсюда легко получить выражения для переменных x1 , x2 , ..., xr через xr+1 , xr+2 , ..., xn . Переменные
x1 , x2 , ..., xr называют базисными переменными, а переменные xr+1 , xr+2 , ..., xn — свободными переменными.
Перенеся свободные переменные в правую часть, получим формулы

которые определяют общее решение системы.
Положим последовательно значения свободных переменных равными
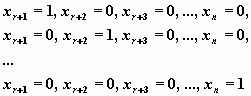
и вычислим соответствующие значения базисных переменных. Полученные n-r решений линейно независимы и, следовательно, образуют фундаментальную систему решений исследуемой однородной системы:
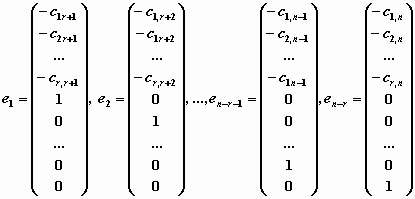
5. Общая теория систем линейных уравнений. Неоднородные системы
Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно n неизвестных
x1 , x2 , ..., xn:
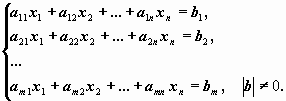
В отличие от однородной системы, эта система совместна не всегда.
Справедливо следующее утверждение (теорема Кронекера-Капелли).
Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
Исследовать неоднородную систему — это значит установить, является ли она совместной, и если является — найти выражение для общего решения системы.
Исследуем неоднородную систему методом Гаусса.
Пусть
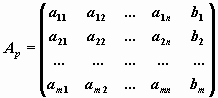
расширенная матрица исследуемой системы, ранг которой r равен рангу матрицы системы и r< n.
Такая матрица приводится Гауссовым исключением к ступенчатому виду
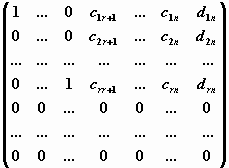 .
.
Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения базисных переменных x1 , x2 , ..., xr через свободные переменные xr+1 , xr+2 , ..., xn . Формулы
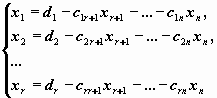
определяют общее решение системы. Положив свободные переменные равными нулю, xr+1 =0, xr+2 =0, ..., xn=0, и вычислив соответствующие значения базисных переменных, получим частное решениеисследуемой системы
x1 =d1 , x2 =d2 , ..., xr=dr , xr+1 =0, xr+2 =0, ..., xn=0.
6. Линейное пространство. Основные понятия
Линейное пространство. Основные понятия
Пусть ![]()
![]() множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
паре элементов множества ![]() ,
, ![]() отвечает элемент
отвечает элемент ![]() , называемый суммой
, называемый суммой ![]() и
и ![]() ;
;
паре ![]() ,
, ![]() отвечает элемент
отвечает элемент ![]() , называемый произведением числа
, называемый произведением числа ![]() и элемента
и элемента ![]() .
.
Будем называть множество ![]() линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов
линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов ![]() и произвольных чисел
и произвольных чисел ![]() справедливо:
справедливо:
-
![[Graphics:16.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_16.gif) , сложение коммутативно;
, сложение коммутативно; -
![[Graphics:17.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_17.gif) , сложение ассоциативно;
, сложение ассоциативно; -
существует единственный нулевой элемент
![[Graphics:18.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_18.gif) такой, что
такой, что ![[Graphics:19.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_19.gif) ,
, ![[Graphics:20.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_20.gif) ;
; -
для каждого элемента существует единственный противоположный элемент
![[Graphics:21.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_21.gif) такой, что
такой, что ![[Graphics:22.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_22.gif) ,
, ![[Graphics:23.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_23.gif)
-
![[Graphics:24.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_24.gif) , умножение на число ассоциативно;
, умножение на число ассоциативно; -
![[Graphics:25.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_25.gif) ,
, ![[Graphics:26.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_26.gif) ;
; -
![[Graphics:27.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_27.gif) , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов; -
![[Graphics:28.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_28.gif) , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
Равенства 1--8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы -- векторами.
Базис и размерность линейного пространства. Координаты вектора в заданном базисе
Говорят, что элемент (вектор) ![]() линейного пространства
линейного пространства ![]() линейно выражается через элементы (векторы)
линейно выражается через элементы (векторы) ![]() , если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде
, если его можно представить в виде линейной комбинации этих элементов, т.е. представить в виде ![]() .
.
Если любой вектор системы ![]() векторов линейного пространства
векторов линейного пространства ![]() линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
Система векторов, которая не является линейно зависимой, называется линейно независимой.
Справедливо следующее утверждение.
Система ![]() векторов линейного пространства
векторов линейного пространства ![]() линейно независима тогда и только тогда, когда из равенства
линейно независима тогда и только тогда, когда из равенства ![]() следует равенство нулю всех коэффициентов
следует равенство нулю всех коэффициентов ![]() .
.
Если в линейном пространстве ![]() существует линейно независимая система из
существует линейно независимая система из ![]() векторов, а любая система из
векторов, а любая система из ![]() -го вектора линейно зависима, то число
-го вектора линейно зависима, то число ![]() называется размерностью пространства
называется размерностью пространства ![]() и обозначается
и обозначается ![]() . В этом случае пространство
. В этом случае пространство ![]() называют
называют ![]() -мерным линейным пространствомили
-мерным линейным пространствомили ![]() -мерным векторным пространством.
-мерным векторным пространством.
Любая упорядоченная линейно независимая система ![]() векторов
векторов ![]() линейного пространства
линейного пространства ![]() образует базис пространства и любой вектор
образует базис пространства и любой вектор ![]() единственным образом выражается через векторы базиса:
единственным образом выражается через векторы базиса: ![]() .
.
Числа ![]() называют координатами вектора
называют координатами вектора ![]() в базисе
в базисе ![]() и обозначают
и обозначают ![]() . При этом для любых двух произвольных векторов
. При этом для любых двух произвольных векторов ![]() -мерного линейного пространства
-мерного линейного пространства ![]() ,
, ![]() и произвольного числа
и произвольного числа ![]() справедливо:
справедливо: ![]() и
и ![]() .
.
Это означает, что все ![]() -мерные линейные пространства “устроены” одинаково -- как пространство
-мерные линейные пространства “устроены” одинаково -- как пространство ![]() векторов-столбцов из
векторов-столбцов из ![]() действительных чисел, т.е. что все они изоморфны пространству
действительных чисел, т.е. что все они изоморфны пространству ![]() .
.
Линейные пространства ![]() и
и ![]() называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам
называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам ![]() и
и ![]() из
из ![]() соответствуют векторы
соответствуют векторы ![]() и
и ![]() из
из ![]() , то вектору
, то вектору ![]() соответствует вектор
соответствует вектор ![]() и при любом
и при любом ![]() вектору
вектору ![]() соответствует вектор
соответствует вектор ![]() .
.
Изоморфизм ![]() -мерных линейных пространств пространству
-мерных линейных пространств пространству ![]() означает, что соотношения между элементами
означает, что соотношения между элементами ![]() -мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из
-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из ![]() и операции с ними и что всякое утверждение относительно векторов из
и операции с ними и что всякое утверждение относительно векторов из ![]() справедливо для соответствующих элементов любого
справедливо для соответствующих элементов любого ![]() -мерного линейного пространства.
-мерного линейного пространства.
Например, доказано, что система векторов ![]() из
из ![]()
![[Graphics:88.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_88.gif) ,
, ![[Graphics:89.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_89.gif) ,...,
,..., ![[Graphics:90.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_90.gif)
образует базис в ![]() тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами
тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами ![]() :
:
![[Graphics:93.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_93.gif)
Для векторов ![]() из
из ![]() это означает, что они образуют базис в
это означает, что они образуют базис в ![]() тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов
тогда и только тогда, когда отличен от нуля определитель матрицы, столбцами которой являются компоненты векторов ![]() .
.
Пусть ![]() и
и ![]() -- два базиса в
-- два базиса в ![]() . Матрицей перехода от базиса
. Матрицей перехода от базиса ![]() к базису
к базису ![]() называется матрица
называется матрица ![]() , столбцами которой являются координаты векторов
, столбцами которой являются координаты векторов ![]() в базисе
в базисе ![]() :
:
| ... | ... |
![]()
![[Graphics:113.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_113.gif) ,
, ![]()
Вектор ![]() линейно выражается через векторы обоих базисов. Тогда, если
линейно выражается через векторы обоих базисов. Тогда, если ![]() , то координаты вектора
, то координаты вектора ![]() в базисе
в базисе ![]() , и его координаты в базисе связаны соотношениями
, и его координаты в базисе связаны соотношениями
![[Graphics:120.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_120.gif)
Исследование линейной зависимости. Ранг матрицы
Пусть ![]() -- прямоугольная матрица размерности
-- прямоугольная матрица размерности ![]() :
:
![[Graphics:123.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_123.gif)
Столбцы матрицы можно рассматривать как векторы из ![]() :
:
![[Graphics:125.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_125.gif) ,
, ![]() ,
,
и исследовать их на линейную зависимость. Исследовать систему векторов на линейную зависимость -- это значит установить является система векторов линейно зависимой или нет.
Доказано, что ранг матрицы равен максимальному числу линейно независимых столбцов матрицы. Это утверждение позволяет исследовать систему векторов ![]() на линейную зависимость следующим образом.
на линейную зависимость следующим образом.
Пусть ![]() -- исследуемая система векторов. Запишем матрицу , столбцами которой являются векторы : , , и вычислим ее ранг . Если
-- исследуемая система векторов. Запишем матрицу , столбцами которой являются векторы : , , и вычислим ее ранг . Если ![]() , то исследуемая система векторов линейно независима, если же , то она линейно зависима.
, то исследуемая система векторов линейно независима, если же , то она линейно зависима.
Более того, если матрица приведена к ступенчатому виду элементарными операциями со строками
то векторы-столбцы , входящие в базисный минор, образуют линейно независимую подсистему, а векторы следующим образом линейно выражаются через базисные векторы:
| ... |
Ортонормированные базисы и ортогональные матрицы
Линейное пространство называется евклидовым, если каждой паре векторов , из этого пространства поставлено в соответствие действительное число , называемое скалярным произведением, и при этом для любых из и любого действительного числа справедливы следующие равенства:
1. ;
2. ;
3. ;
4. при , , -- нулевой вектор.
Число называется длиной вектора ; число -- расстоянием между векторами ; угол , косинус которого , -- углом между векторами , , , .
Векторы , из евклидова пространства называются ортогональными, если .
Система векторов евклидова пространства называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину.
Базис конечномерного евклидова пространства называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину. Поскольку доказано, что в любом конечномерном евклидовом пространстве существует ортонормированный базис, будем рассматривать в -мерном евклидовом пространстве только ортонормированные базисы.
Простейший пример евклидова пространства дает нам пространство -- пространство столбцов, в котором скалярное произведение введено формулой .
Тогда для любых , из справедливы формулы:
Все евклидовы пространства размерности устроены так же, как пространство .
Величины ![]() ,
, ![]() и характеризуют взаимное расположение векторов и не зависят от выбранного ортонормированного базиса.
и характеризуют взаимное расположение векторов и не зависят от выбранного ортонормированного базиса.
Если и -- два ортонормированных базиса в ![]() -мерном евклидовом пространстве, то матрица перехода от одного из этих базисов к другому -- ортогональная матрица.
-мерном евклидовом пространстве, то матрица перехода от одного из этих базисов к другому -- ортогональная матрица.
7. Элементарная теория линейных операторов
Пусть заданы линейные пространства ![]() и
и ![]() . Правило, по которому каждому элементу
. Правило, по которому каждому элементу ![]() ставится в соответствие единственный элемент
ставится в соответствие единственный элемент ![]() , называется оператором, действующим в линейных пространствах
, называется оператором, действующим в линейных пространствах ![]() . Результат действия оператора
. Результат действия оператора ![]() на элемент
на элемент ![]() обозначают
обозначают ![]() или
или ![]() . Если элементы
. Если элементы ![]() и
и ![]() связаны соотношением
связаны соотношением ![]() , то
, то ![]() называют образом элемента
называют образом элемента ![]() ; элемент
; элемент ![]() прообразом элемента
прообразом элемента ![]() .
.
Множество элементов линейного пространства ![]() , для которых определено действие оператора
, для которых определено действие оператора ![]() , называют областью определения оператора и обозначают
, называют областью определения оператора и обозначают ![]() .
.
Множество элементов линейного пространства ![]() , которые являются образами элементов из области определения оператора
, которые являются образами элементов из области определения оператора ![]() , называют образом оператора и обозначают
, называют образом оператора и обозначают ![]() . Если
. Если ![]() , то
, то ![]() .
.
Оператор ![]() , действующий в линейных пространствах
, действующий в линейных пространствах ![]() называется линейным оператором, если
называется линейным оператором, если ![]() и
и ![]() для любых
для любых ![]() и для любого числа
и для любого числа ![]() .
.
Если пространства ![]() и
и ![]() совпадают, то говорят, что оператор действует в пространстве
совпадают, то говорят, что оператор действует в пространстве ![]() . В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве
. В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве ![]() .
.
Линейный оператор и его матрица. Переход к другому базису
Рассмотрим линейный оператор ![]() , действующий в конечномерном линейном пространстве
, действующий в конечномерном линейном пространстве ![]() ,
, ![]() и пусть
и пусть ![]() базис в
базис в ![]() . Обозначим через
. Обозначим через ![]() образы базисных векторов
образы базисных векторов ![]() .
.
Матрица
![[Graphics:42.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_42(1).gif)
столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.
Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно ![]() каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
![[Graphics:44.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/primery-po-kursu-lineynoy-algebry933/index_gr_44(1).gif)
с одной стороны, связывают координаты образа ![]() с координатами прообраза
с координатами прообраза ![]() , с другой стороны, описывают действие оператора, заданного матрицей
, с другой стороны, описывают действие оператора, заданного матрицей ![]() .
.
При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве ![]() произошел переход от базиса
произошел переход от базиса ![]() к базису
к базису ![]() . Связь между матрицей
. Связь между матрицей ![]() оператора
оператора ![]() в базисе
в базисе ![]() и матрицей
и матрицей ![]() этого оператора в базисе
этого оператора в базисе ![]() задается формулой .
задается формулой .
![]()
Здесь ![]()
![]() матрица перехода от базиса
матрица перехода от базиса ![]() к базису
к базису ![]() и обратная к ней.
и обратная к ней.
Образ и ядро линейного оператора
Рассмотрим линейный оператор ![]() , действующий в конечномерном линейном пространстве
, действующий в конечномерном линейном пространстве ![]() . Доказано, что образ
. Доказано, что образ ![]() линейного оператора
линейного оператора ![]() линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается
линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается ![]() .
.
Ядром линейного оператора называется множество элементов из ![]() , образом которых является нулевой элемент. Ядро оператора обозначают
, образом которых является нулевой элемент. Ядро оператора обозначают ![]() :
: ![]() . Ядро линейного оператора
. Ядро линейного оператора ![]() линейное пространство; размерность ядра линейного оператора называется дефектом оператора, обозначается
линейное пространство; размерность ядра линейного оператора называется дефектом оператора, обозначается ![]() :
: ![]() .
.
Для линейного оператора, действующего в n-мерном линейном пространстве ![]() , справедливы следующие утверждения:
, справедливы следующие утверждения:
сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ![]() ;
;
ранг оператора равен рангу его матрицы;
ядро оператора совпадает с множеством решений линейной однородной системы с матрицей ![]() , размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.
Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
Собственные значения и собственные векторы линейного оператора
Пусть ![]()
![]() линейный оператор, действующий в линейном пространстве.
линейный оператор, действующий в линейном пространстве.
Число ![]() называется собственным значением, а ненулевой вектор
называется собственным значением, а ненулевой вектор ![]()
![]() соответствующим собственным вектором линейного оператора
соответствующим собственным вектором линейного оператора ![]() , если они связаны между собой соотношением
, если они связаны между собой соотношением ![]() .
.
Пусть ![]() матрица оператора в некотором базисе.
матрица оператора в некотором базисе.
Собственные значения оператора и соответствующие им собственные векторы связаны соотношением ![]() , где
, где ![]() единичная матрица, а
единичная матрица, а ![]() нулевой элемент пространства
нулевой элемент пространства ![]() . Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы
. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы ![]() , которое существует тогда и только тогда, когда
, которое существует тогда и только тогда, когда ![]() . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения
. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения ![]() , а собственные векторы -- как решения соответствующих однородных систем.
, а собственные векторы -- как решения соответствующих однородных систем.
Уравнение ![]() называется характеристическим уравнением оператора, а многочлен
называется характеристическим уравнением оператора, а многочлен ![]() характеристическим многочленом оператора.
характеристическим многочленом оператора.
Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:
характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно ![]() ;
;
линейный оператор, действующий в n-мерном линейном пространстве имеет не более ![]() различных собственных значений;
различных собственных значений;
собственные векторы, отвечающие различным собственным значениям, линейно независимы;
если линейный оператор, действующий в n-мерном линейном пространстве ![]() , имеет
, имеет ![]() различных собственных значений, то собственные векторы оператора образуют базис в пространстве
различных собственных значений, то собственные векторы оператора образуют базис в пространстве ![]() ; этот базис называют собственным базисом оператора;
; этот базис называют собственным базисом оператора;
матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.
Комментарии