Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документация MATLAB на русском языке.

Матрица как математический объект возникает при решении конкретных вычислительных задач, и в первую очередь при решении систем линейных алгебраических уравнений и задач на собственные значения. Матрица в виде прямоугольной таблицы чисел очень схожа с массивом, однако прикладные задачи, которые порождают матрицы, определяют для них специальную совокупность допустимых операций, среди которых особое место занимает операция умножения. Для простейшего случая, когда умножается вектор-строка на вектор-столбец, такой операцией является операция скалярного произведения.

Матрицы широко используются при решении обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных, решении оптимальных задач и т. п.

Алгебраические задачи, связанные с матрицами, объединяются в раздел математики, получивший название линейной алгебры, который включает такие базисные задачи, как обращение и псевдообращение матриц, спектральное и сингулярное разложение матриц.

В вычислительном плане раздел линейной алгебры поддержан пакетами прикладных программ LINPACK, EISPACK, разработанными в 60-70-е годы ведущими специалистами, к числу которых принадлежит и основатель фирмы The MathWorks, Inc. Моулер (C. Moler). Изначальное назначение системы MATLAB состояло именно в том, чтобы создать диалоговую среду для работы с пакетами программ линейной алгебры.

Несмотря на кажущуюся завершенность, этот раздел развивается и в настоящее время в направлении создания новых операций: для работы с парами матриц (приведение пары матриц к форме Шура, рекуррентное сингулярное разложение пары прямоугольных матриц), решения матричных полиномов и полиномиальных матричных уравнений.

Рассмотрим функции системы MATLAB, которые поддерживают работу с матрицами, в следующей последовательности: характеристики матриц, решение систем линейных уравнений, вычисление собственных значений и сингулярных чисел, вычисление функций от матриц, работа с алгебраическими полиномами.

Матрицы широко используются при решении обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных, решении оптимальных задач и т. п.

Алгебраические задачи, связанные с матрицами, объединяются в раздел математики, получивший название линейной алгебры, который включает такие базисные задачи, как обращение и псевдообращение матриц, спектральное и сингулярное разложение матриц.

В вычислительном плане раздел линейной алгебры поддержан пакетами прикладных программ LINPACK, EISPACK, разработанными в 60-70-е годы ведущими специалистами, к числу которых принадлежит и основатель фирмы The MathWorks, Inc. Моулер (C. Moler). Изначальное назначение системы MATLAB состояло именно в том, чтобы создать диалоговую среду для работы с пакетами программ линейной алгебры.

Несмотря на кажущуюся завершенность, этот раздел развивается и в настоящее время в направлении создания новых операций: для работы с парами матриц (приведение пары матриц к форме Шура, рекуррентное сингулярное разложение пары прямоугольных матриц), решения матричных полиномов и полиномиальных матричных уравнений.

Рассмотрим функции системы MATLAB, которые поддерживают работу с матрицами, в следующей последовательности: характеристики матриц, решение систем линейных уравнений, вычисление собственных значений и сингулярных чисел, вычисление функций от матриц, работа с алгебраическими полиномами.

Характеристики матриц

• COND - число обусловленности матрицы
• NORM - нормы векторов и матриц
• RCOND - оценка числа обусловленности матрицы
• RANK - ранг матрицы
• DET - определитель матрицы
• TRACE - след матрицы
• NULL - нуль-пространство (ядро) матрицы
• ORTH - ортонормальный базис матрицы
• SUBSPACE - угол между двумя подпространствами
• RREF - треугольная форма матрицы

Решение линейных уравнений

• \, / - решатели систем линейных уравнений
• CHOL - разложение Холецкого
• LU - LU-разложение
• INV - обращение матрицы
• PINV - псевдообращение матрицы по Муру-Пенроузу
• QR, QRDELETE, QRINSERT - QR-разложение
• PLANEROT - преобразование Гивенса
• NNLS - метод наименьших квадратов с ограничениями
• LSCOV - метод наименьших квадратов в присутствии шумов

Вычисление собственных значений и сингулярных чисел

• EIG, CDF2RDF - собственные значения и собственные векторы матрицы
• BALANCE - масштабирование матрицы
• HESS - приведение к форме Хессенберга
• SCHUR, RSF2CSF - приведение к форме Шура
• CPLXPAIR - сортировка комплексносопряженных пар
• QZ - прведение пары матриц к обобщенной форме Шура
• POLYEIG - вычисление собственных значений матричного полинома
• SVD - сингулярное разложение матрицы

Вычисление функций от матриц

• EXPM, EXPM1, EXPM2, EXPM3 - вычисление матричной экспоненты
• LOGM - вычисление логарифма матрицы
• SQRTM - вычисление функции A ^1/2
• FUNM - вычисление произвольных функций от матрицы

Полиномы и операции над ними

• POLYVAL - вычисление полинома
• POLYVALM - вычисление матричного полинома
• CONV - умножение полиномов
• DECONV - деление полиномов
• POLYDER - вычисление производных
• ROOTS - вычисление корней полиномов
• POLY - вычисление характеристического полинома
• RESIDUE, RESI2 - разложение на простые дроби

Характеристики матриц

 

Наверх

COND - число обусловленности матрицы

Синтаксис:

k = cond(A)

Описание:

Функция k = cond(A) возвращает число обусловленности матрицы A по отношению к операции обращения, которое равно отношению максимального сингулярного числа к минимальному:

k = s _max/s _min.

Число обусловленности по отношению к операции обращения - это мера относительной погрешности, равная
k = ||D(A-1)||/||DA||,
где ||DA|| - норма матрицы погрешностей исходных данных. Оно характеризует точность операции обращения матрицы или решения системы линейных уравнений.

Эта функция неприменима для разреженных матриц.

Сопутствующие функции: CONDEST, RCOND, NORM, SVD.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

NORM - нормы векторов и матриц

Синтаксис:

	n = norm(v, p)	n = norm(A, p)
	n = norm(v)	n = norm(A, ‘fro’)
		n = norm(A)

Описание:

Нормы векторов:

Функция n = norm(v, p) вычисляет p-норму вектора v, определяемую следующим образом:

            || v ||_p = sum(abs(v).^p)^1/p.

Cправедливы следующие соотношения:

            norm(v) = norm(v, 2);
            norm(v, inf) = max(abs(v));
            norm(v, -inf) = min(abs(v)).

Нормы матриц:

Функция n = norm(A, p) вычисляет подчиненную p-норму матрицы A только для значений p, равных 1, 2, inf.

Cправедливы следующие соотношения:

            norm(A, 1) = max(sum(abs(A)));
            norm(A, inf) = max(sum(abs(A’)));
            norm(A, ‘fro’) = sqrt(sum(diag(A’ * A)));
            norm(A) = norm(A, 2) = smax(A).

Пример:

Нормы вектора:	Нормы матрицы:
v = -3 : 2;	A = toeplitz(1:5, 1.5:4.5);
norm(v, 1) ans = 9.0000	norm(A, 1) ans = 15
norm(v, 2) ans = 4.3589	norm(A, 2) ans = 12.1001
norm(v, 3) ans = 3.5569	norm(A, inf) ans = 14
norm(v, inf) ans = 3	norm(A, 'fro') ans = 12.9422
norm(v, -inf) ans = 0	norm(A) ans = 12.1001
norm(v) ans = 4.3589

Сопутствующие функции: COND, RCOND, SVD, MIN, MAX.

 

Наверх

RCOND - оценка числа обусловленности матрицы

Синтаксис:

             k_1 = rcond(A)

Описание:

Функция k_1 = rcond(A) возвращает величину, обратную значению числа обусловленности матрицы A относительно 1-нормы. Если матрица A хорошо обусловлена, то значение k_1 близко к единице; если матрица A плохо обусловлена, то значение k_1 близко к нулю.

Пример:

A = hilb(4);

	1/rcond(A)	cond(A)	condest(A)
	2.1523e+004	1.5514e+004	2.8375e+004

Сопутствующие функции: COND, NORM, SVD, RANK, CONDEST.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

RANK - ранг матрицы

Синтаксис:

             r = rank(A)
             r = rank(A, tol)

Описание:

Функция r = rank(A) возвращает ранг матрицы, который определяется как количество сингулярных чисел, превышающих порог max(size(A))*norm(A)*eps.

Функция r = rank(A, tol) возвращает ранг матрицы, который определяется как количество сингулярных чисел, превышающих заданный порог tol.

Алгоритм:

Существует несколько подходов к вычислению ранга матрицы. В системе MATLAB использован метод, основанный на вычислении сингулярных чисел матрицы A; он реализован в виде функции svd. Это наиболее надежный метод, хотя и требующий значительного времени на вычисление.

Сам алгоритм вычисления ранга достаточно прост:

            s = svd(A);
            tol = max(size(A)) * s(1) * eps;
            r = sum(s > tol).

Сопутствующие функции: SVD.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

DET - определитель матрицы

Синтаксис:

            d = det(A)

Описание:

Функция d = det(A) вычисляет определитель квадратной матрицы; если матрица A целочисленная, то результатом является также целое число.

Алгоритм:

Определитель матрицы вычисляется на основе треугольного разложения методом исключения Гаусса:

            [L, U] = lu(A);
            s = det(L);
            d = s * prod(diag(U)).

Пример:

Вычисление определителя и ранга матриц Гильберта различного порядка.

n	3	4	5	6	7	8	9	10	11
det	4.6296 e-004	1.6534 e-007	3.7493 e-012	5.3673 e-018	4.8358 e-025	2.7371 e-033	9.7203 e-043	2.1645 e-053	3.0274 e-065
rank	3	4	5	6	7	8	9	10	11

Сопутствующие функции: INV, LU, RCOND, RREF, /, \.

 

Наверх

TRACE - след матрицы

Синтаксис:

t = trace(A)

Описание:

Функция t = trace(A) вычисляет след квадратной матрицы, равный сумме ее диагональных элементов.

Алгоритм:

Алгоритм вычисления следа матрицы на языке MATLAB - это однострочный М-файл

t = sum(diag(A)).

Пример:

Вычисление следа, определителя и ранга матриц Гильберта различного порядка.

n	3	4	5	6	7	8	9	10	11
trace	1.5333	1.6762	1.7873	1.8782	1.9551	2.0218	2.0806	2.1333	2.1809
det	4.6296 e-004	1.6534 e-007	3.7493 e-012	5.3673 e-018	4.8358 e-025	2.7371 e-033	9.7203 e-043	2.1645 e-053	3.0274 e-065
rank	3	4	5	6	7	8	9	10	11

Сопутствующие функции: DET, EIG.

 

Наверх

NULL - нуль-пространство (ядро) матрицы

Синтаксис:

             Q = null(A)

Описание:

Функция Q = null(A) возвращает ортонормальный базис нуль-пространства матрицы A; если Q - не пустая матрица, то справедливы следующие соотношения:

Q’ * Q = eye(size(A));
A * Q = 0.

Количество столбцов матрицы Q определяет размерность нуль-пространства или дефект матрицы A, что можно вычислить следующим образом:

             defect = size(null(A), 2).

Пример:

Вычисление дефекта, следа, определителя и ранга матриц Гильберта различного порядка.

n	4	5	6	7	8	9	10	11	12
defect	0	0	0	0	0	0	0	0	1
trace	1.6762	1.7873	1.8782	1.9551	2.0218	2.0806	2.1333	2.1809	2.2244
det	1.6534 e-007	3.7493 e-012	5.3673 e-018	4.8358 e-025	2.7371 e-033	9.7203 e-043	2.1645 e-053	3.0274 e-065	2.7904 e-078
rank	4	5	6	7	8	9	10	11	12

Сопутствующие функции: QR, ORTH, SUBSPACE.

 

Наверх

ORTH - ортонормальный базис матрицы

Синтаксис:

             Q = orth(A)

Описание:

Функция Q = orth(A) возвращает ортонормальный базис матрицы A; столбцы Q определяют то же пространство, которая определяет и столбцы A, но столбцы Q ортогональны, то есть

Q’ * Q = eye(size(A)).

Количество столбцов матрицы Q определяет ранг матрицы A, что можно вычислить следующим образом:

                rank = size(orth(A), 2).

Пример:

Вычисление ранга матриц Гильберта различного порядка:

n	4	5	6	7	8	9	10	11	12
rank	4	5	6	7	8	9	10	10	11

Сопутствующие функции: QR, NULL, SUBSPACE.

 

Наверх

SUBSPACE - угол между двумя подпространствами

Синтаксис:

             theta = subspace(A, B)

Описание:

Функция theta = subspace(A, B) возвращает угол между двумя подпространствами, натянутыми на столбцы матриц A и B; если a и b - векторы единичной длины, то вычисляется угол между двумя векторами theta = acos(a’ * b).

Если некоторая реализация физического эксперимента описывается массивом A, а другая реализация - массивом B, то функция subspace(A, B) определяет меру количества новой информации, полученной из второго эксперимента и не связанную со случайными ошибками.

Сопутствующие функции: NULL, QR, ORTH.

 

Наверх

RREF - треугольная форма матрицы

Синтаксис:

	R = rref(A)	[R, jb] = rref(A)	rrefmovie(A)
	R = rref(A, tol)	[R, jb] = rref(A, tol)	rrefmovie(A, tol)
			rrefmovie

Описание:

Функция R = rref(A) осуществляет приведение матрицы к треугольной форме на основе метода исключения Гаусса с частичным выбором ведущего элемента.

По умолчанию используется следующее значение порога для принятия решения о малости исключаемого элемента:

             tol = max(size(A) * eps * norm(A, inf).

Функция R = rref(A, tol) осуществляет приведение матрицы к треугольной форме на основе метода исключения Гаусса с частичным выбором ведущего элемента для заданного значения порога tol.

Функции [R, jb] = rref(A) и [R, jb] = rref(A, tol) кроме треугольной формы возвращают также вектор jb, обладающий следующими свойствами:

• r = length(jb) может служить оценкой ранга матрицы A;
• при решении систем линейных уравнений Ax = b переменные x(jb) являются связанными переменными;
• столбцы A(:, jb) определяют базис матрицы A;
• R(1 : r, jb) - единичная.

Функции R = rrefmovie(A) и R = rrefmovie(A, tol) реализуют пошаговую процедуру приведения матрицы к треугольной форме с выводом на экран промежуточных матриц.

Функции R = rrefmovie демонстрирует пошаговую процедуру приведения некоторой матрицы размера 8 х 6 с рангом 4 к треугольной форме.

Примеры:

            A = magic(4), [R, jb]=rref(A)

A =	R =
16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1	1 0 0 1 0 1 0 3 0 0 1 -3 0 0 0 0

jb =    1     2    3
r = length(jb)
r = 3

A(:, jb) =	R(:, jb) =
16 2 3 5 11 10 9 7 6 4 14 15	1 0 0 0 1 0 0 0 1 0 0 0

Сопутствующие функции: RANK, ORTH, LU, INV.

 

 

Наверх

Решение линейных уравнений

 

Наверх

\, / - решатели систем линейных уравнений

Синтаксис:

X = B \ A
X = B / A

Описание:

Функция X = A \ B находит решение системы уравнений вида AX = B, где A - прямоугольная матрица размера m х n и B - матрица размера n х k.

Функция X = B / A находит решение системы уравнений вида XA = B, где A - прямоугольная матрица размера n х m и B - матрица размера m х k.

Алгоритм:

Решение систем линейных уравнений вида X = A \ B и X = B / A реализовано в MATLAB с помощью специального монитора, который использует разные алгоритмы решения в зависимости от структуры матрицы A.

• Если A - треугольная матрица с точностью до перестановки ее строк или столбцов, то решение таких систем уравнений может быть эффективно вычислено методом обратной подстановки. Проверка матрицы, является ли она верхней треугольной, осуществляется для полных матриц проверкой на нуль всех элементов, лежащих ниже диагонали; для разреженных матриц - определением структуры ее элементов. Большинство матриц нетреугольной структуры выявляются почти мгновенно, так что такая проверка требует очень малого времени.
• Если матрица A - симметрическая или эрмитова с положительными диагональными элементами, то применяется разложение Холецкого (функция chol). Если A - разреженная матрица, применяется алгоритм упорядочения по разреженности (функции symmmd и spparms). Если при этом матрица A положительно определенна, то алгоритм Холецкого позволяет эффективно найти решение. Матрицы, не являющиеся положительно определенными, выявляются почти мгновенно. Разложение Холецкого имеет вид:
  A = L * L^T,
  где L^T - верхняя треугольная матрица. После этого решение Х можно получить решая последовательно две треугольные системы
  X = L^T \ (L \ B).
• Если A - произвольная квадратная матрица, то треугольное разложение вычисляется методом исключения Гаусса с частичным выбором главного элемента (функция lu). Если A - разреженная матрица, применяется алгоритм упорядочения по разреженности столбцов (функции colmmd и spparms). В результате имеем следующее разложение:
  A = L * U,
  где L - нижняя, а U - верхняя треугольные матрицы. После этого решение Х можно получить решая последовательно две треугольные системы
  X = U \ (L \ B).
• Если A - прямоугольная полная матрица, то применяется QR-разложение на основе преобразований Хаусхолдера следующего вида
  A * P = Q * R,
  где P - матрица преобразований, Q - ортогональная и R - верхняя треугольная (функция qr) матрицы. Решение, соответствующее минимуму квадрата ошибки, находится согласно следующему соотношению
  X = P * (R \ (QT * B)).
• Если A - прямоугольная разреженная матрица, то формируется вспомогательная расширенная матрица следующего вида:
  S = [c*I A; A^T 0].
  Это реализуется с помощью функции spaugment. По умолчанию значение коэффициента масштабирования невязки c равно max(max(abs(A)))/1000 (функция spparms). Решение X в соответствии с методом наименьших квадратов и матрица невязок R = B - A * X вычисляются путем решения следующей системы:
  S * [R / c; X] = [B; 0]
  с использованием алгоритмов упорядочения по разреженности и исключения Гаусса с выбором главного элемента.
  Различные алгоритмы разложения матриц реализованы в системе MATLAB на основе ZGECO, ZGEFA и ZGESL для квадратных и процедур ZQRDC и ZQRSL для прямоугольных матриц из пакета LINPACK [1].

Диагностические сообщения:

При решении систем линейных уравнений:
если A - квадратная вырожденная матрица, выдается сообщение Matrix is singular to working precision.

Для выбранной точности матрица вырожденна.

При поэлементном делении:
если массив-делитель имеет нулевые элементы, выдается сообщение

Divide by zero.
Деление на нуль.

На ЭВМ, где не реализован стандарт IEEE-арифметики, например на ЭВМ VAX, обе вышеприведенные операции будут выдавать сообщения об ошибке. На ЭВМ, где реализован стандарт IEEE-арифметики, например на РС, будут генерироваться только предупреждения. При этом при решении систем будут возвращаться матрицы, часть элементов которых будет иметь значение Inf; при поэлементном делении результатом могут быть как значения Inf, так и значение NaN.

Если результат обращения матрицы не является надежным, выдается сообщение

            Warning: Matrix is close to singular or badly scaled.
            Results may be inaccurate. RCOND = xxx
            Предупреждение: Матрица близка к вырожденной или плохо масштабирована.
            Результаты могут быть неточными. Число обусловленности RCOND = xxx

При решении систем линейных уравнений:
если прямоугольная матрица А имеет неполный столбцовый ранг, выдается сообщение

            Warning: Rank deficient, rank = xxx tol = xxx
            Предупреждение: Неполный ранг, ранг rank = xxx точность tol = xxx

Сопутствующие функции: INV, QR, DET, LU, RCOND, ORTH, RREF.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

CHOL - разложение Холецкого

Синтаксис:

             R = chol(A)
             [R, p] = chol(A)

Описание:

Функция R = chol(A) находит разложение Холецкого для действительных симметрических и комплексных эрмитовых матриц. Если A - положительно определенная матрица, то матрица R - верхняя треугольная и удовлетворяет соотношению R’ * R = A; в противном случае появляется сообщение об ошибке.

Функция [R, p] = chol(A) никогда не генерирует сообщения об ошибке; если A - положительно определенная матрица, то p = 0 и матрица R совпадает с предшествующим случаем, в противном случае p > 0 и R - верхняя треугольная матрица порядка q = p -1 такая, что R’ * R = A(1 : q, 1 : q).

Примеры:

Рассмотрим матрицу Паскаля, составленную из биномиальных коэффициентов. Это положительно определенная матрица, а ее разложение Холецкого также использует часть биномиальных коэффициентов:

A = pascal(5)

A	R = chol(A)	eig(A)
1 1 1 1 1 1 2 3 4 5 1 3 6 10 15 1 4 10 20 35 1 5 15 35 70	1 1 1 1 1 0 1 2 3 4 0 0 1 3 6 0 0 0 1 4 0 0 0 0 1	0.0108 1.1812 1.0000 5.5175 92.2904

Разрушим положительную определенность этой матрицы, вычтя из ее последнего элемента единицу:

A	[R, p] = chol(A)	eig(A)
1 1 1 1 1 1 2 3 4 5 1 3 6 10 15 1 4 10 20 35 1 5 15 35 69	1 1 1 1 0 1 2 3 0 0 1 3 0 0 0 1 p = 5	0.0000 0.1500 0.9522 5.3531 91.5446

            R' * R =

	1	1	1	1
	1	2	3	4
	1	3	6	10
	1	4	10	20

Сопутствующие функции: QR, LU.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

LU - LU-разложение

Синтаксис:

             [L, U] = lu(A)
             [L, U, P] = lu(A)

Описание:

Функция [L, U] = lu(A) находит LU-разложение для произвольной квадратной матрицы A в виде произведения нижней треугольной матрицы L (возможно с перестановками) и верхней треугольной матрицы U, так что A = L * U.

Функция [L, U, P] = lu(A) находит разложение для произвольной квадратной матрицы A в виде трех составляющих - нижней треугольной матрицы L, верхней треугольной матрицы U и матрицы перестановок P, так что P * A = L * U.

Все алгоритмы LU-разложения так или иначе основаны на методе исключения Гаусса. LU-разложение используется при вычислении определителей, нахождении обратных матриц и в решателях систем линейных уравнений.

Примеры:

Рассмотрим возмущенную отрицательно определенную матрицу Паскаля 3-го порядка следующего вида:

	A =	eig(A) =
	1 1 1 1 2 3 1 3 4	0.7024 -0.2185 6.5160

            [L, U] = lu(A)

L =	U =	L * U =
1.0000 0 0 1.0000 0.5000 1.0000 1.0000 1.0000 0	1.0000 1.0000 1.0000 0 2.0000 3.0000 0 0 0.5000	1 1 1 1 2 3 1 3 4

            det(A) = det(L) * det(U) = -1;
            [L, U, P] = lu(B)

L =	U =	P =	L * U =
1.0000 0 0 1.0000 0.5000 0 1.0000 1.0000 1.0000	1.0000 1.0000 1.0000 0 2.0000 3.0000 0 0 0.5000	1 0 0 0 0 1 0 1 0	1 1 1 1 2 3 1 3 4

det(A) = det(L) * det(U)/det(P) = -1;

Сопутствующие функции: QR, INV, DET, RCOND, RREF, \, /.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

INV - обращение матрицы

Синтаксис:

             Y = inv(A)

Описание:

Функция Y = inv(A) вычисляет матрицу, обратную квадратной матрице A. В случаях, когда матрица A плохо масштабирована или близка к вырожденной, выдаются сообщения.

На практике вычисление явной обратной матрицы требуется не так часто. Как правило, говоря о задаче обращения, имеют в виду нахождение решений систем линейных уравнений. В рамках системы MATLAB для этих целей рекомендуется использовать решатели систем, то есть операторы вида x = A\b или x = b/ A, а не операцию x = inv(A)*b.

Диагностические сообщения:

В процессе выполнения функции inv на рабочих станциях и компьютерах с IEEE-арифметикой возможно появление следующего предупреждения:

Matrix is singular to working precision.
               При заданной точности матрица вырожденна.

При этом формируется матрица, все элементы которой равны Inf.

На машинах без IEEE-арифметики, например на VAX, эта ситуация рассматривается как ошибка.

Если выполненное обращение ненадежно, появляется сообщение

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = xxx
               Предупреждение: Матрица близка к вырожденной. Результаты могут быть неточными. RCOND = xxx

Примеры:

Рассмотрим пример, демонстрирующий различие в определении решения систем линейных уравнений с помощью операций x = inv(A) * b и x = A \ b.

Cформируем матрицу Кахана A = kahan(100,1.35); со следующими характеристиками:

                 cond(A) = 1.6203e+010 norm(A) = 8.2970,

используя пакет Test Matrix Toolbox.

Затем сформируем результат в виде случайного вектора x = rand(100, 1);, а затем вычислим вектор b = A * x.

Используя компьютер PC/AT 486 с тактовой частотой 50 МГц, выполним следующие расчеты с фиксацией продолжительности вычислений:

t0 = clock;		t0 = clock;
y = inv(A) * b;		z = A \ b;
t = etime(clock, t0)		t = etime(clock, t0)
t = 1.0400		t = 0.0600
err = norm(y - x)		err = norm(z - x)
err = 2.3224e-008		err = 1.1668e-008
res = norm(A * y - b)		res = norm(A * z - b)
res = 2.5831e-008		res = 1.0409e-014

Сравнивая оба подхода, можно убедиться, что расчеты с помощью решателя выполняются значительно быстрее и с большей точностью.

Сопутствующие функции: DET, LU, RCOND, RREF, \, /.

Ссылки:

1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

PINV - псевдообращение матрицы по Муру-Пенроузу

Синтаксис:

P = pinv(A)
P = pinv(A, tol)

Описание:

Функция P = pinv(A) вычисляет матрицу, псевдообратную матрице A, которая имеет такие же размеры, как и матрица A’, и удовлетворяет следующим условиям [1]:

A * P * A = A;
P * A * P = P.

Вычисление матрицы P основано на использовании функции svd(A) и приравнивании к нулю всех сингулярных чисел, меньших величины tol, которая по умолчанию принимается равной tol = max(size(A)) * norm(A) * eps.

Функция P = pinv(A, tol) позволяет пользователю самому назначить порог tol.

Если матрица A квадратная и невырожденная, то вычисление обратной на основе псевдообращения является слишком расточительной процедурой. Если A - квадратная и вырожденная или прямоугольная матрица, то обратной матрицы не существует; в этих случаях псевдообратная матрица обладает некоторыми, но не всеми свойствами обратной.

Если A имеет строк больше, чем столбцов, и не является матрицей полного ранга, то возникает переопределенная задача наименьших квадратов

Вектор x минимизирует указанную норму тогда и только тогда, когда x имеет вид

x = pinv(A) * b + (I - pinv(A) * A) * z

для некоторого z.

Выберем два из бесконечного множества решений:

x = pinv(A) * b;
               y = A \ b.

Эти решения характеризуются следующими свойствами: решение x имеет норму norm(x), которая минимальна в сравнении с нормой любого другого решения; решение y имеет минимальное количество ненулевых компонентов.

Пример:

Рассмотрим прямоугольную матрицу, которая генерируется следующим образом:

A = magic(8); A = A(:, 1:6).

Эта матрица размером 8 х 6 имеет ранг, равный 3.

Сформируем вектор b = 260 * ones(8, 1).

Тогда получим следующие решения

x = pinv(A) * b x =   1.1538   1.4615   1.3846   1.3846   1.4615   1.1538 norm(x) = 3.2817

y = A \ b Warning: Rank deficient, rank = 3 tol = 1.8829e-013 Предупреждение: Ранг неполный, rank = 3 tol = 1.8829e-013 y =   3.0000   4.0000   0   0   1.0000   0 norm(y) = 5.0990

Вектор z, удовлетворяющий условию y = x + (I - pinv(A) * A) * z, равен

z’ = [ 5.7517    9.6751     4.6404    5.8559    7.8906     1.5362 ]

Сопутствующие функции: RANK, INV, SVD, QR.

Ссылки:

1. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание: Пер. с англ. М.:Наука, 1977. 224 с.

 

Наверх

QR, QRDELETE, QRINSERT - QR-разложение

Синтаксис:

[Q, R] = qr(A)	Q, R] = qrdelete(Q, R, j)	[Q, R] = qrinsert(Q, R, j, x)
[Q, R, P] = qr(A)
Y = qr(A)

Описание:

Функция [Q, R] = qr(A) находит QR-разложение для произвольной матрицы A в виде произведения унитарной матрицы Q и верхней треугольной матрицы R, так что A = Q * R.

Функция [Q, R, P] = qr(A) находит разложение для произвольной квадратной матрицы A в виде трех составляющих - унитарной матрицы Q, верхней треугольной матрицы R с убывающими по модулю диагональными элементами и матрицы перестановок P, так что A * P = Q * R.

Функция Y = qr(A) возвращает матрицу Y, которая связана с матрицей R соотношением R = triu(Y).

Функция [Q, R] = qrdelete(Q, R, j) позволяет пересчитать известное QR-разложение матрицы A для случая, когда в матрице A удален j-й столбец A(:, j). Функция [Q, R] = qrinsert(Q, R, j, x) позволяет пересчитать известное QR-разложение матрицы A для случая, когда в матрице A перед j-м столбцом A(:, j) вставлен дополнительный столбец x. Если указать j = n+1, где n - число столбцов матрицы A, то дополнительный столбец x будет n+1-м столбцом матрицы.

Примеры:

Рассмотрим операции, связанные с QR-разложением следующей прямоугольной матрицы A:

             [Q, R] = qr(A)

A =	Q =	R =
1 2 3 4 5 6 7 8 9 10 11 12	-0.0776 -0.8331 0.5444 0.0605 -0.3105 -0.4512 -0.7709 0.3251 -0.5433 -0.0694 -0.0913 -0.8317 -0.7762 0.3124 0.3178 0.4461	-12.8841 -14.5916 -16.2992 0 -1.0413 -2.0826 0 0 0.0000 0 0 0

Удалим второй столбец из матрицы A:

             [Q1, R1] = qrdelete(Q, R, 2)

Q1 =	R1 =
-0.0776 -0.8331 0.5444 0.0605 -0.3105 -0.4512 -0.7709 0.3251 -0.5433 -0.0694 -0.0913 -0.8317 -0.7762 0.3124 0.3178 0.4461	-12.8841 -16.2992 0 -2.0826 0 0 0 0

Вставим второй столбец из матрицы A на место третьего:

            [Q2, R2] = qrinsert(Q1, R1, 3, A(:,2))

Q2 =	R 2=
-0.0776 0.8331 -0.5458 -0.0456 -0.3105 0.4512 0.6938 0.4676 -0.5433 0.0694 0.2499 -0.7985 -0.7762 -0.3124 -0.3979 0.3764	-12.8841 -16.2992 -14.5916 0 2.0826 1.0413 0 0 0.0000 0 0 0	1 3 2 4 6 5 7 9 8 10 12 11

Сопутствующие функции: ORTH, NULL, LU, \, /.

Ссылки: 1. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

Наверх

PLANEROT - преобразование Гивенса

Синтаксис:

             [G, y] = planerot(x)

Описание:

Функция [G, y] = planerot(x), где x - вектор-столбец из двух компонентов, возвращает ортогональную матрицу G порядка 2, такую, что выполняется условие y = Gx и y(2) = 0.

Преобразование Гивенса применяется для исключения элементов матрицы с целью ее приведения к более простой форме (Хессенберга, трехдиагональной и т. п.).

Сопутствующие функции: QRINSERT, QRDELETE.

 

Наверх

NNLS - метод наименьших квадратов с ограничениями

Синтаксис:

	x = nnls(A, b)	[x, w] = nnls(A, b)
	x = nnls(A, b, tol)	[x, w] = nnls(A, b, tol)

Описание:

Функция x = nnls(A, b) находит неотрицательные решения xj >= 0, j = 1,..., n для системы уравнений вида Ax = b по методу наименьших квадратов. Для отбора таких решений по умолчанию используется значение порога tol = max(size(A)) * norm(A,1) * eps.

Функция x = nnls(A, b, tol) позволяет пользователю самому установить значение порога tol.

Функции [x, w] = nnls(A, b) и [x, w] = nnls(A, b, tol) позволяют в дополнение к решению x возвратить также вектор двойственных переменных w. Векторы x и w связаны между собой следующими соотношениями:

wi < 0, (i | xi = 0);
wi = 0, (i | xi > 0).

Пример:

Сравним решения задачи наименьших квадратов с ограничениями и без них. Пусть задана следующая система уравнений, описываемая парой {A, b}

	A =		b =
	0.0372 0.2869 0.6861 0.7071 0.6233 0.6245 0.6344 0.6170		0.8587 0.1781 0.0747 0.8405

Вычислим решения без ограничений и с ограничениями на переменные, а также нормы невязок:

[ A\b     nnls(A, b) ]	[norm(A * (A \ b) - b)	norm(A * nnls(A, b) - b)]
-2.5627 0 3.1108 0.6929	0.6674	0.9118

Как следует из решения, невязка для решения без ограничений меньше, но при этом один из компонентов вектора x отрицателен.

Найдем вектор двойственных переменных w:

[x, w] = nnls(A, b)

	x =		w =
	0 0.6929		-0.1506 0.0000

Сопутствующие функции: LSCOV.

Ссылки:

1. Lawson C. L., Hanson R. J. Solving Least Squares Problems. Prentice-Hall, 1974.

 

Наверх

LSCOV - метод наименьших квадратов в присутствии шумов

Синтаксис:

x = lscov(A, b, V)

Описание:

Функция x = lscov(A, b, V) возвращает решение x для следующей системы уравнений Ax = b + v, где вектор шумов v имеет матрицу ковариаций V. Решение минимизирует по методу наименьших квадратов следующую квадратичную форму:

             (Ax - b)’ * inv(V) * (Ax - b).

Решение задачи имеет вид [1, 2]:

x = inv(A’ * inv(V) * A) * A’ * inv(V) * b.

Реально алгоритм построен так, что обращения матрицы V не требуется.

Сопутствующие функции: QR, NNLS.

Ссылки:

1. Strang G. Introduction to Applied Mathematics. Wellesley-Cambridge, 1986.
2. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание: Пер. с англ. М.:Наука, 1977. 224 с.

 

 

Вычисление собственных значений и сингулярных чисел

 

Наверх

EIG, CDF2RDF - собственные значения и собственные векторы матрицы

Синтаксис:

	d = eig(A)	d = eig(A, B)
	[R, D] = eig(A)	[V, D] = eig(A, B)
	[R, D] = eig(A, ‘nobalance’)
	[R, D] = cdf2rdf(R, D)

Описание:

Проблема собственных значений состоит в нахождении нетривиальных решений системы уравнений, которая может быть интерпретирована как алгебраический эквивалент системы обыкновенных дифференциальных уравнений в явной форме Коши:

Ar = l r,

где A - квадратная матрица порядка n;
      r - вектор-столбец размера 1х n, называемый собственным вектором;
      l - скаляр, называемый собственным значением.

Функция d = eig(A) вычисляет собственные значения матрицы A.

Функция [R, D] = eig(A) вычисляет диагональную матрицу D собственных значений и матрицу R правых собственных векторов, удовлетворяющих соотношению A * R = R * D. Эти векторы нормированы так, что норма каждого из них равна единице.

Левые собственные векторы могут быть найдены следующим образом:
[L, D] = eig(A’);

Матрицы собственных значений D для A и A’ содержат одни и те же собственные значения, хотя порядок их следования может быть различен. Матрица левых собственных векторов удовлетворяет соотношению A’ * L = L * D. Для согласования независимо найденных систем правых и левых собственных векторов систему левых векторов необходимо нормировать так, чтобы соблюдалось условие L * R = eye(n,n).

Функция [R, D] = cdf2rdf(R, D) преобразовывает комплексные выходы функции   eig в действительные, при этом комплексные собственные значения преобразовываются в блоки размера 2 х 2, а комплексная матрица правых собственных векторов R преобразовывается в действительную, столбцы которой, соответствующие действительным собственным значениям, сохраняются, а соответствующие комплексным - расщепляются на два: [Re(ri) Im(ri)].

Пример 1:

Рассмотрим матрицу порядка 3 с одним действительным и парой комплексно сопряженных собственных значений и выполним вычисления с использованием комплексных матриц.

Применяя функцию cdf2rdf, эти же вычисления можно реализовать, используя только действительные матрицы, что позволяет более экономно расходовать память.

Функция [R, D] = eig(A, ‘nobalance’) вычисляет собственные значения и собственные векторы без предварительного масштабирования матрицы. Обычно, масштабирование улучшает обусловленность матрицы, гарантируя большую точность вычислений. Однако когда матрица содержит очень малые по величине элементы, которые находятся в пределах ошибок округления, масштабирование может сделать их сравнимыми с другими элементами матрицы, что может привести к неправильным результатам.

Пример 2:

Рассмотрим матрицу порядка 4, которая содержит элементы, сравнимые с ошибками округления.

B = ;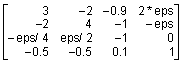

[RB, DB] = eig(B);					RN, DN] = eig(B, 'nobalance');
DB =					DN =
5.5616	0	0	0		5.5616
0	1.4384	0	0			1.4384
0	0	1.0000	0				1.0000
0	0	0	-1.0000					-1.0000
norm(B * RB - RB * DB) = 1.24392					norm(B*RN- RN*DN) = 0.9957e-015

Как следует из этого примера, собственные значения в обоих случаях вычислены правильно, но нормы невязок различаются очень существенно, что свидетельствует о том, что собственные векторы в первом случае вычислены неверно.

Обобщенная проблема собственных значений состоит в нахождении нетривиальных решений системы уравнений

Ar = l Br,

где A, B - квадратные матрицы порядка n;
      r - вектор-столбец размера 1 х n, называемый обобщенным собственным вектором;
      l - скаляр, называемый обобщенным собственным значением.

Вычисления с использованием комплексных матриц:

Вычисления с использованием только действительных матриц:

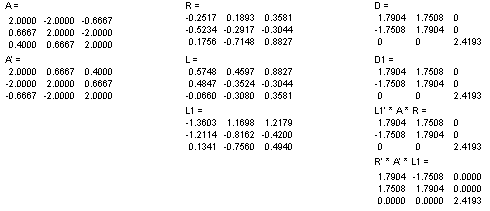
Если B - невырожденная матрица, то система может быть рассмотрена как алгебраический эквивалент системы обыкновенных дифференциальных уравнений в неявной форме Коши, а задача может быть сведена к обычной проблеме собственных значений

B^-1Ar = l r.

В случае, когда B - вырожденная матрица, система уравнений представляет собой смешанную систему дифференциальных и алгебраических уравнений и для ее решения необходимо применять специальные методы.

Функция d = eig(A, B) вычисляет обобщенные собственные значения матрицы A.

Функция [R, D] = eig(A, B) вычисляет диагональную матрицу D обобщенных собственных значений и матрицу R правых обобщенных собственных векторов, удовлетворяющих соотношению A * R = B * R * D. Эти векторы нормированы так, что норма каждого из них равна единице.

Алгоритм:

Для действительных матриц функция eig(A) использует следующие модули пакета EISPACK [1-2]: balance, balbak, orthes, ortran и hqr2. Модули balance и balbak связаны с операциями масштабирования и восстановления; модуль orthes осуществляет приведение матрицы к форме Хессенберга посредством ортогональных подобных преобразований; модуль ortran запоминает все преобразования; модуль hqr2 вычисляет собственные значения и векторы матрицы в верхней форме Хессенберга с использованием QR-алгоритма Франсиса и Кублановской [3].

Функция eig(A, B) использует другие модули пакета EISPACK [1-2]: qzhes, qzit, qzval, и qzvec, основанные на QZ-алгоритме.

Для комплексных матриц функция eig(A) использует QZ-алгоритм, решая задачу в форме eig(A, eye(A)).

Диагностические сообщения:

Если в течение 30*n итераций собственные значения не найдены, выдается сообщение
          Solution will not converge.
          Решение не сходится.

Сопутствующие функции: BALANCE, HESS, QZ, SCHUR.

Ссылки:

1. Smith B. T., Boyle J. M., Dongarra J. J., Garbow B. S., Ikebe Y., Klema V., Moler C. B.. Matrix Eigensystem Routines - EISPACK//Guide. Lecture Notes in Computer Science. Berlin, 1976. Vol. 6.
2. Garbow B. S., Boyle J. M., Dongarra J. J., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide Extension//Lecture Notes in Computer Science. Berlin, 1977. Vol. 51.
3. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 390 с.
4. Moler C. B., Stewart G. W. An Algorithm for Generalized Matrix Eigenvalue Problems//SIAM J. Numer. Anal. 1973. N 2. Vol. 10.

 

Наверх

BALANCE - масштабирование матрицы

Синтаксис:

            B = balance(A)
            [D, B] = balance(A)

Описание:

Несимметрические матрицы могут проявлять плохую обусловленность при вычислении их собственных значений. Малые возмущения элементов матрицы, такие, как ошибки округления, могут вызывать значительные погрешности в собственных значениях. Величина, связывающая погрешность вычисления собственных значений с погрешностью исходных данных, называется числом обусловленности задачи на собственные значения и вычисляется следующим образом:

             k = cond(R) = norm(R) * norm(inv(R)), где [R, D] = eig(A).

Цель масштабирования - перевести плохую обусловленность матрицы собственных векторов в диагональное масштабирование. Масштабирование не может превратить несимметрическую матрицу в симметрическую, но делается попытка выравнять нормы строк и соответствующих столбцов. Поскольку масштабирование реализуется введением множителей, которые являются степенями основания 2, то никаких ошибок округления при этом не привносится.

Функция B = balance(A) возвращает масштабированную матрицу.

Функция [D, B] = balance(A) кроме масштабированной матрицы возвращает также диагональную матрицу D, элементы которой являются степенями основания 2; матрица B - это результат преобразования подобия

            B = D \ A * D.

Функция eig(A) автоматически масштабирует A перед вычислением собственных значений D. Масштабирование можно подавить, если использовать обращение вида eig(A, ‘nobalance’).

Пример:

Рассмотрим матрицу порядка 3, которая имеет большой разброс значений элементов - большие наддиагональные и малые поддиагональные элементы.

	A =	1	100	10000
		0.01	1	100
		0.0001	0.01	1

Вычислим собственные значения и векторы матрицы A.

[RA, DA] = eig(A)

A =	RA =	DA =
1.0e+004* 0.0001 0.0100 1.0000 0.0000 0.0001 0.0100 0.0000 0.0000 0.0001	0.9999 -1.0000 -0.9998 0.0100 0.0054 0.0209 0.0001 0.0000 -0.0001 cond(RA) = 1.4073e+004	3.0000 0 0 0 0.0000 0 0 0 0.0000

Матрица собственных векторов плохо обусловлена.

Выполним масштабирование матрицы A.

[D, B] = balance(A)

A =	D =	B =
1.0e+004* 0.0001 0.0100 1.0000 0.0000 0.0001 0.0100 0.0000 0.0000 0.0001	1.0e+003 * 2.0480 0 0 0 0.0320 0 0 0 0.0003 cond(D) = 8192	1.0000 1.5625 1.2207 0.6400 1.0000 0.7813 0.8192 1.2800 1.0000

После масштабирования значения элементов матрицы B оказались выравненными по величине.

Вычислим собственные значения и векторы матрицы B.

            [RB, DB] = eig(B)

B =	RB =	DB =
1.0000 1.5625 1.2207 0.6400 1.0000 0.7813 0.8192 1.2800 1.0000	0.6933 -0.8903 -0.5274 0.4437 0.3070 0.7064 0.5679 0.3364 -0.4721 cond(RB) = 1.9381	3.0000 0 0 0 0.0000 0 0 0 0.0000

Матрица собственных векторов очень хорошо обусловлена. Плохая обусловленность сконцентрирована в диагональной матрице масштабирования D.

Алгоритм: Функция balance является встроенной функцией интерпретатора MATLAB; она использует алгоритмы, первоначально написанные на языке АЛГОЛ [1], а затем реализованные на языке FORTRAN в составе пакета EISPACK: balance, balbak [2].

Ограничения:

Обычно масштабирование улучшает обусловленность матрицы, гарантируя большую точность вычислений. Однако когда матрица содержит очень малые по величине элементы, которые находятся в пределах ошибок округления, масштабирование может сделать их сравнимыми с другими элементами матрицы, что может привести к неправильным результатам.

Диагностические сообщения:

Если матрица не квадратная, выдается сообщение
          Matrix must be square.
          Матрица должна быть квадратной.

Сопутствующие функции: EIG, HESS, SCHUR.

Ссылки:

1. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 390 с.
2. Garbow B. S., Boyle J. M., Dongarra J. J., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide Extension//Lecture Notes in Computer Science. Berlin, 1977. Vol. 51.

 

Наверх

HESS - приведение к форме Хессенберга

Синтаксис:

            H = hess(A)
            [P, H] = hess(A)

Описание:

Функция H = hess(A) возвращает матрицу в верхней форме Хессенберга, элементы которой hij c номерами i > j + 1, то есть расположенные ниже первой поддиагонали, равны нулю. Если матрица A симметрическая или эрмитова, то матрица Хессенберга вырождается в трехдиагональную.

Функция [P, H] = hess(A) кроме матрицы в верхней форме Хессенберга возвращает также унитарную матрицу преобразований P, которая удовлетворяет условиям

A = P * H * P, P’ * P = eye(size(A)).

Пример:

Рассмотрим приведение матрицы A = magic(5) размером 5 х 5 к верхней форме Хессенберга.

A = magic(5), H = hess(A)

A =	H =
17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9	17.0000 -28.9413 1.8470 -4.4603 2.2572 -27.6767 33.9399 26.1875 -2.2280 1.2675 0 25.0964 20.6871 -6.6055 -0.1973 0 0 -5.9630 -16.8163 -12.4454 0 0 0 -9.0122 10.1893

Алгоритм:

Для действительных матриц функция hess(A) использует следующие модули пакета EISPACK [1-2]: ortran и orthes. Модуль orthes осуществляет приведение матрицы к верхней форме Хессенберга посредством ортогональных подобных преобразований; модуль ortran запоминает все преобразования.

Для комплексных матриц функция hess(A) использует модуль qzhes пакета EISPACK.

Сопутствующие функции: EIG, QZ, SCHUR.

Ссылки:

1. Smith B. T., Boyle J. M., Dongarra J. J., Garbow B. S., Ikebe Y., Klema V., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide//Lecture Notes in Computer Science. Berlin, 1976. 1976. Vol. 6.
2. Garbow B. S., Boyle J. M., Dongarra J. J., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide Extension//Lecture Notes in Computer Science. Berlin, 1977. Vol. 51.

 

Наверх

SCHUR, RSF2CSF - приведение к форме Шура

Синтаксис:

            T = schur(A)
            [U, T] = schur(A)
            [U, T] = rsf2csf(U,T)

Описание:

Функция T = schur(A) возвращает матрицу в форме Шура. Комплексная форма Шура - это верхняя треугольная матрица с собственными значениями на диагонали; действительная форма Шура сохраняет на диагонали действительные собственные значения, а комплексные представляются в виде блоков 2 х 2, частично занимая нижнюю поддиагональ.

Функция [U, T] = schur(A) кроме матрицы Шура T возвращает также унитарную матрицу преобразований U, которая удовлетворяет условиям

A = U * H * U’, U’ * U = eye(size(A)).

Если исходная матрица A действительная, то возвращается действительная форма Шура, если комплексная, то комплексная форма Шура. Функции cdf2rdf и rsf2csf обеспечивают преобразование из одной формы в другую.

Функция [U, T] = rsf2csf(U, T) преобразовывает действительную квазитреугольную форму Шура в комплексную треугольную.

Пример:

Рассмотрим приведение тестовой матрицы с двумя кратными комплексными и одним действительным собственными значениями к действительной форме Шура [1].

	A =	15	11	6	-9	-15
		1	3	9	-3	-8
		7	6	6	-3	-11
		7	7	5	-3	-11
		17	12	5	-10	-16

         [U, T] = schur(A)

U =

0.2868 0.0207 0.7227 0.2502 -0.5766 0.4854 0.4640 -0.5919 0.1372 -0.4241 0.4192 0.0148 0.0802 0.6744 0.6023 0.3530 0.5466 0.3290 -0.5861 0.3533 0.6178 -0.6966 -0.1129 -0.3467 -0.0096

 

T =

-1.0000 20.1766 4.8432 33.1468 15.2146 0 -0.0399 -2.0829 -2.2176 8.8043 0 7.2596 3.0399 10.1089 -10.9556 0 0 0 0.7171 2.7149 0 0 0 -4.9221 2.2829

Преобразуем действительную квазитреугольную форму Шура в комплексную треугольную.

             [U1, T1] = rsf2csf(U, T)
   U1 =

0.2868	0.6332 + 0.0090i	-0.1534 - 0.3133i	0.4310 + 0.1457I	0.2745 + 0.3358i
0.4854	-0.6085 + 0.2012i	-0.2984 + 0.2566i	0.3230 + 0.0799I	0.1643 + 0.2470i
0.4192	0.0680 + 0.0064i	-0.0280 - 0.0348i	-0.5696 + 0.3928I	0.4645 - 0.3508i
0.3530	0.1878 + 0.2370i	-0.5434 - 0.1426i	-0.2088 - 0.3413I	-0.5156 - 0.2058i
0.6178	0.0307 - 0.3020i	0.6352 + 0.0490i	0.0520 - 0.2019I	-0.2771 + 0.0056i

     T1 =

-1.0000	0.4967 + 8.7481i	-18.6913 - 2.0999i	7.9820 +19.3046I	28.5534 + 8.8610i
0	1.5000 + 3.5707I	-5.8300 - 1.5148i	7.3239 + 8.3731I	6.7070 + 7.8425i
0	0	1.5000 - 3.5707i	2.0252 + 3.2914I	-1.9851 + 7.4522i
0	0	0	1.5000 - 3.5707I	2.4562 + 1.1359i
0	0	0	0	1.5000 - 3.5707i

Алгоритм:

Для действительных матриц функция schur(A) использует следующие модули пакета EISPACK [2-3]: ortran, orthes и hqr2. Модуль orthes осуществляет приведение матрицы к верхней форме Хессенберга посредством ортогональных подобных преобразований; модуль ortran запоминает все преобразования. Модуль hqr2 вычисляет собственные значения матрицы в верхней форме Хессенберга на основе QR-алгоритма Франсиса - Кублановской.

Для комплексных матриц функция schur(A) использует модули qzhes, qzit, qzval и qzvec пакета EISPACK.

Сопутствующие функции: HESS, EIG, QZ.

Ссылки:

1. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 390 с.
2. Smith B. T., Boyle J. M., Dongarra J. J., Garbow B. S., Ikebe Y., Klema V., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide//Lecture Notes in Computer Science. Berlin, 1976. Vol. 6.
3. Garbow B. S., Boyle J. M., Dongarra J. J., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide Extension//Lecture Notes in Computer Science. Berlin, 1977. Vol. 51.

 

Наверх

CPLXPAIR - сортировка комплексносопряженных пар

Синтаксис:

             y = cplxpair(x)
             y = cplxpair(x, tol)

Описание:

Функция y = cplxpair(x) группирует комплексно сопряженные пары элементов вектора в порядке возрастания их действительных частей. Внутри пары элемент с отрицательной мнимой частью всегда является первым. Действительные элементы замыкают комплексно сопряженные пары. Порог отделения комплексных элементов от действительных по умолчанию равен imag(x(i))/abs(x(i)) < 100*eps.

Функция y="cplxpair(x," tol) позволяет пользователю указать свой порог отделения комплексных элементов от действительных.

В результате выполнения этой функции все комплексно сопряженные пары, возможно вычисленные неточно в пределах погрешности вычисления, выравниваются.

Пример: Произведем сортировку элементов вектора x="exp(2" * pi * i * (0 : 4) / 5), расположенных на окружности единичного радиуса.

 

Наверх

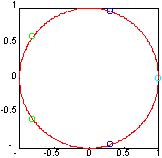
QZ - прведение пары матриц к обобщенной форме Шура

Синтаксис:

[AA, BB, Q, Z, V] = qz(A, B)

Описание:

Многие задачи линейной алгебры - решение матричных уравнений Сильвестра и Риккати, смешанныx систем дифференциальных и линейных алгебраических уравнений, приводят к необходимости одновременного приведения пары матриц к форме Шура.

Функция [AA, BB, Q, Z, V] = qz(A, B) возвращает комплексные верхние треугольные матрицы AA и BB, соответствующие матрицы приведения Q и Z, а также вектор обобщенных собственных векторов V, так что

            Q * A * Z = AA;
            Q * B * Z = BB.

Обобщенные собственные значения могут быть найдены исходя из следующего условия:

            A * V * diag(BB) = B * V * diag(AA).

Пример:

Для системы обыкновенных дифференциальных уравнений в неявной форме Коши с одним входом и одним выходом

            

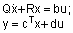
задачи вычисления полюсов и нулей соответствующей передаточной функции определяются следующим образом [1]:

• вычисление полюсов
  Rr = -lQr;
• вычисление нулей

                     .

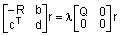Нетрудно видеть, что обе задачи требуют решения обобщенной проблемы собственных значений.

Описание системы:

Q =	R =	b =
1.0000 0 0.1920 1.0000	1.1190 -1.0000 36.4800 1.5380	31.0960 0.1284
C = [ 0.6299 0 ]	d = -0.0723

Расчет полюсов:

            [AA, BB] = qz(R, -Q)

AA =

5.5039 + 2.7975i 24.8121 - 25.3646i 0.0000 + 0.0000i 5.5158 - 2.8036i

BB =	diag(AA)./diag(BB) =
-0.6457 + 0.7622i -0.1337 + 0.1378i 0 -0.6471 - 0.7638i	-1.4245 - 6.0143i -1.4245 + 6.0143i

Расчет нулей:

	A = [-R b        C d]	B = [ -Q       zeros(size(b))          zeros(size(C))         0 ]
	-1.1190 1.0000 0.1284 -36.4800 -1.5380 31.0960 0.6299 0 0.0723	-1.0000 0 0 -0.1920 -1.0000 0 0 0 0

[AA, BB] = qz(A, B)

AA =	BB =	diag(AA)./diag(BB) =
31.0963 -0.7165 -36.5109 0.0000 1.0647 0.9229 0 0.0000 0.5119	0 0.9860 -0.2574 0 0.0657 0.9964 0 0 -0.0354	Inf 16.2035 -14.4735

Алгоритм:

Средством вычисления формы Шура для пары матриц {A, B} является созданный Моулером и Стьюартом QZ-алгоритм [2-3], который реализован в рамках пакета EISPACK [4] и использует модули qzhes, qzit, qzval и qzvec.

Сопутствующие функции: EIG.

Ссылки:

1. Потемкин В. Г., Кутузова Г. Н. Особенности исследования дискретно-непрерывных комплексов на ЭВМ. Учеб. пособие. М.: МИФИ, 1988. 56 с.
2. Икрамов Х. Д. Численное решение матричных уравнений. М.: Наука, 1984. 192 с.
3. Moler C. B., Stewart G. W. An Algorithm for Generalized Matrix Eigenvalue Problems//SIAM J. Numer. Anal. 1973. N 2. Vol. 10.
4. Garbow B. S., Boyle J. M., Dongarra J. J., Moler C. B. Matrix Eigensystem Routines - EISPACK Guide Extension//Lecture Notes in Computer Science. Berlin, 1977. Vol. 51.

 

Наверх

POLYEIG - вычисление собственных значений матричного полинома

Синтаксис:

[R, d] = polyeig(A₀, A₁, ..., A_p)

Описание:

Функция [R, d] = polyeig(A₀, A₁, ..., A_p) решает полную проблему собственных значений для матричного полинома степени p вида

         (A₀ + l * A₁ + ... + l ^p * A_p) * r = 0.

Входными переменными этой функции являются p+1 квадратная матрица A₀, A₁, ..., A_p порядка n. Выходными переменными - матрица собственных векторов R размера n х (n х p) и вектор собственных значений d длины n х p.

Для некоторых значений p и n функция polyeig становится равносильной другим функциям системы MATLAB:

• p = 0, функция polyeig(A) равносильна функции eig(A);
• p = 1, функция polyeig(A, B) равносильна функции eig(A, -B);
• n = 1, функция polyeig(a0, a1, ..., ap) для скаляров a0, ..., ap, равносильна функции roots([ap .. a1 a0]).

Алгоритм:

Задача сводится к решению обобщенной проблемы собственных значений для пары матриц A и B порядка n х p. В частном случае, когда p = 4, эти матрицы имеют вид

    A = 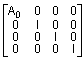;        B = ;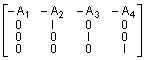

Если одна (но не обе) из матриц A₀ или A_p вырожденна, то некоторые из собственных значений могут оказаться равными нулю или Inf.

Если обе матрицы A₀ и A_p вырожденны, то задача оказывается плохо обусловленной. С точки зрения теории это означает, что решения может не существовать или оно может быть неединственным. С вычислительной точки зрения решение может оказаться неточным.

В алгоритме сделана попытка выявить эту ситуацию и сформировать соответствующее предупреждение.

Диагностические сообщения:

Если обе матрицы A₀ и A_p близки к вырожденным, выдается сообщение
Warning: Rank deficient generalized eigenvalue problem.
Eigenvalues are not well determined. Results may be inaccurate.
Предупреждение: Неполный ранг для обобщенной проблемы.
Собственные значения плохо обусловлены. Результат может быть неточным.

Замечание:

Функция polyeig включена в систему MATLAB начиная с версии 4.2c.

Сопутствующие функции: EIG, ROOTS, QZ.

 

Наверх

SVD - сингулярное разложение матрицы

Синтаксис:

            s = svd(A)
            [U, S, V] = svd(A)
            [U, S, V] = svd(A, 0)

Описание:

Если A - действительная матрица размера m х n (m >= n), то ее можно представить в виде [1]:

            A = U * S * V^T,

где U^TU = V * V^T = In и S = diag(s₁, ...s_n).

Такое разложение называется сингулярным разложением матрицы A.

Матрица U сформирована из n ортонормированных собственных векторов, соответствующих n наибольшим собственным значениям матрицы AA^T, а матрица V - из ортонормированных собственных векторов матрицы A^TA. Диагональные элементы матрицы S - неотрицательные значения квадратных корней из собственных значений матрицы A^TA; они называются сингулярными числами.

Допустим, что s₁>= s₂ >=... >= s_n >= 0. Если ранг матрицы A равен r, то значения s_r+1 = s_r+2 = ... = s_n = 0.

Существует другое, более экономное сингулярное разложение:

            A = U_r * S_r * V_r^T,

где U_r^TU_r = V_r * V_r^T = I_r и S_r = diag(s₁, ..., s_r).

Функция s = svd(A) вычисляет только сингулярные числа матрицы A.

Функция [U, S, V] = svd(A) вычисляет диагональную матрицу S тех же размеров, которые имеет и матрица A с неотрицательными диагональными элементами в порядке их убывания, а также унитарные матрицы преобразований U и V.

Функция [U, S, V] = svd(A, 0) выполняет экономное сингулярное разложение.

Пример 1: Рассмотрим прямоугольную матрицу размера 4 х 2.

A =

	1	2
	3	4
	5	6
	7	8

Полное сингулярное разложение

            [U, S, V] = svd(A)

U =	V =	S =
0.1525 0.8226 -0.3945 -0.3800 0.3499 0.4214 0.2428 0.8007 0.5474 0.0201 0.6979 -0.4614 0.7448 -0.3812 -0.5462 0.0407	0.6414 -0.7672 0.7672 0.6414	14.2691 0 0 0.6268 0 0 0 0

Экономное сингулярное разложение

[U, S, V] = svd(A, 0)

U =	V =	S =
0.1525 0.8226 0.3499 0.4214 0.5474 0.0201 0.7448 -0.3812	0.6414 -0.7672 0.7672 0.6414	14.2691 0 0 0.6268

Пример 2:

Рассмотрим матрицу порядка 5, которая в пределах ошибок округления имеет только нулевые собственные значения [2].

                 A = chebspec(5)

	A =	5.5000	-6.8284	2.0000	-1.1716	0.5000
		1.7071	-0.7071	-1.4142	0.7071	-0.2929
		-0.5000	1.4142	0.0000	-1.4142	0.5000
		0.2929	-0.7071	1.4142	0.7071	-1.7071
		-0.5000	1.1716	-2.0000	6.8284	-5.5000

                [U, S, V] = svd(A^3)

	U =	0.5774	-0.4472	-0.5412	0.2121	0.3588
		0.4082	-0.4472	0.2245	-0.2794	-0.7106
		0.0000	-0.4472	0.6753	-0.1695	0.5614
		-0.4082	-0.4472	0.0819	0.7588	-0.2256
		-0.5774	-0.4472	-0.4404	-0.5220	0.0159

 

	S =	155.5378	0	0	0	0
		0	32.8634	0	0	0
		0	0	0.0000	0	0
		0	0	0	0.0000	0
		0	0	0	0	0.0000

 

	V =	0.2673	-0.4082	0.6267	-0.5498	0.2588
		-0.5345	0.5774	0.0315	-0.4589	0.4115
		0.5345	0.0000	-0.5883	-0.1319	0.5923
		-0.5345	-0.5774	-0.0528	0.3475	0.5073
		0.2673	0.4082	0.5074	0.5908	0.3943

   

semilogy(svd(A3))	plot(eig(A3)

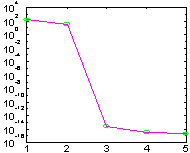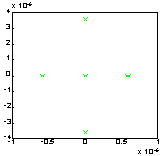Из анализа графиков следует, что 3 сингулярных числа имеют значения меньше 10^-14 и существенно отличаются от остальных; собственные значения находятся в круге радиусом 0.5 * 10^-6, то есть являются кратными. Дефект матрицы A³равен трем.

В рассматриваемом случае это означает, что имеется 3 клетки Жордана, порядок которых пока неизвестен. Применяя пакет прикладных программ JORD [3], можно установить, что в данном случае имеется одна клетка первого и две клетки второго порядка.

Алгоритм:

Функция svd(A) использует модуль svd пакета LINPACK [4].

Пакет программ JORD можно запросить по следующему адресу электронной почты: potem@mephi.ru.

Диагностические сообщения:

Если в течение 75 итераций QR-преобразования сингулярные значения не найдены, выдается сообщение
             Solution will not converge.
             Решение не сходится.

Ссылки:

1. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 390 с.
2. Higham N. J. The Test Matrix Toolbox for MATLAB (version 3.0)//Numerical Analysis Report. Manchester. 1995. Vol. 276.
3. Потемкин В. Г. Пакет программ JORD. М.: МИФИ, 1995.
4. Dongarra J. J., Bunch J. R., Moler C. B., Stewart G. W. LINPACK User’s Guide. Philadelphia, 1979.

 

 

Вычисление функций от матриц

 

Наверх

EXPM, EXPM1, EXPM2, EXPM3 - вычисление матричной экспоненты

Синтаксис:

	Y = expm(A)	Y = expm2(A)
	Y = expm1(A)	Y = expm3(A)

Описание:

Функция Y = expm(A) является встроенной функцией интерпретатора системы MATLAB и вычисляет функцию e^A от матрицы A.

Функция Y = expm1(A) является M-файлом, который полностью соответствует встроенной функции expm(A). Он вычисляет функцию e^A, используя разложение Паде матрицы A [1].

Функция Y = expm2(A) вычисляет функцию e^A, используя разложение Тейлора матрицы A [2]. Этот метод имеет меньшую скорость сходимости по сравнению с разложением Паде.

Функция Y = expm3(A) вычисляет функцию e^A, используя спектральное разложение матрицы A:

             [R, D] = eig(A);
             Y = R * diag(exp(diag(D))) / R;,

которое, строго говоря, справедливо только для случая различных собственных значений.

Замечание:

Функцию матричной экспоненты expm(A) не следует путать с функцией exp(A), которая вычисляет экспоненту от каждого элемента массива A.

Пример:

Рассмотрим тестовую матрицу порядка n = 5 с дефектом 1, имеющую 5 кратных собственных значений, равных нулю [3].

norm(Y1 - Y)	norm(Y1 - Y2)	norm(Y1 - Y3)
0	1.0560e-013	0.0065

Как следует из анализа полученных данных, функции expm(A) и expm1(A) дают совпадающие результаты, функция expm2(A) имеет погрешность в пределах ошибки округления, однако функция expm3(A) имеет ошибки в третьем знаке, что является следствием того, что исходная система меет кратные собственные значения.

Используя пакет программ JORD [4], можно выявить точную структуру формы Жордана матрицы A.

R =	J =
0.2342 0.2342 0.0679 -0.0102 -0.0050 0.2342 0.1656 0.0093 -0.0210 0.0000 0.2342 0.0000 -0.0492 0.0000 0.0099 0.2342 -0.1656 0.0093 0.0210 0.0000 0.2342 -0.2342 0.0679 0.0102 -0.0050	0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0

В данном случае это 1 клетка Жордана порядка 5, характеризующая простую однократную вырожденность.

Аналитическая функция f(J), где J - клетка Жордана, соответствующая собственному значению l, может быть вычислена следующим образом [4]:

f(J) = .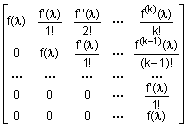

В рассматриваемом случае матрица e^J равна

EJ =

	1.0000	1.0000	0.5000	0.1667	0.0417
	0	1.0000	1.0000	0.5000	0.1667
	0	0	1.0000	1.0000	0.5000
	0	0	0	1.0000	1.0000
	0	0	0	0	1.0000

а матрица Y0 = e^A = R * e^J * R^-1 может быть вычислена так:

Y0 = R * EJ / R.

Вычисленная матрица Y0 имеет вид

Y0 =

	21.0000	-32.4853	21.0000	-15.5147	7.0000
	11.1569	-15.7782	9.2426	-6.5355	2.9142
	1.0000	0.0000	0.0000	0.0000	0.0000
	-0.1569	0.5355	0.7574	-0.2218	0.0858
	0.0000	0.0000	1.0000	0.0000	0.0000

Cчитая данное решение точным, оценим нормы невязок для предыдущих решений.

norm(Y0 - Y)	norm(Y0 - Y1)	norm(Y0 - Y2)	norm(Y0 - Y3)
1.2635e-013	1.2635e-013	6.3827e-014	0.0065

Из анализа следует, что функции expm1(A) и expm2(A) дают результаты с погрешностью в пределах ошибки округления, а функция expm3(A) имеет ту же погрешность.

Сопутствующие функции: EXP, FUNM, LOGM, SQRTM.

Ссылки:

1. Golub G. H., Van Loan. Matrix Computation. Oxford. John Hopkins University Press, 1983.
2. Moler C. B., Van Loan. Nineteen Dubious Ways to Compute the Exponential of a Matrix//SIAM Review, 1979. Vol. 20. P. 801-836.
3. Higham N. J. The Test Matrix Toolbox for MATLAB (version 3.0)//Numerical Analysis Report. Manchester, 1995. Vol. 276.
4. Потемкин В. Г. Пакет программ JORD. М.: МИФИ, 1995.

 

Наверх

LOGM - вычисление логарифма матрицы

Синтаксис:

            Y = logm(A)
            [Y, esterr] = logm(A)

Описание:

Функция Y = logm(A) вычисляет функцию log(A), такую, что для большинства матриц A должно выполняться условие

logm(expm(A)) = A = expm(logm(A)).

При таком обращении возможно появление диагностического предупреждения

Warning: LOGM appears inaccurate. esterr = xxx
          Предупреждение: функция LOGM вычислена неточно. esterr = xxx
Если матрица A - действительная симметрическая или комплексная эрмитова, то теми же свойствами обладает и функция logm(A).

Функция [Y, esterr] = logm(A) кроме вычисленной матрицы возвращает оценку погрешности в виде относительной невязки

norm(expm(Y) - A) / norm(A).

В этом случае диагностическое сообщение не выводится.

Замечание:

Функцию матричной экспоненты logm(A) не следует путать с функцией log(A), которая вычисляет логарифм от каждого элемента массива A.

Пример:

Рассмотрим матрицу A = expm(chebspec(5)), вычисленную в предыдущем разделе.

            A =

	21.0000	-32.4853	21.0000	-15.5147	7.0000
	11.1569	-15.7782	9.2426	-6.5355	2.9142
	1.0000	0.0000	0.0000	0.0000	0.0000
	-0.1569	0.5355	0.7574	-0.2218	0.0858
	0.0000	0.0000	1.0000	0.0000	0.0000

logm(A)
Warning: LOGM appears inaccurate. esterr = 6.471e-007

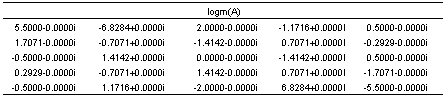
Алгоритм:

Функция logm, как и другие функции от матриц, вычисляется с использованием алгоритма Парлетта [1]. Этот алгоритм использует приведение к форме Шура и может давать неточные или полностью несостоятельные результаты в случае кратных собственных значений.

Сопутствующие функции: EXPM, FUNM, SQRTM.

Ссылки:

1. Golub G. H., Van Loan. Matrix Computation. Oxford. John Hopkins University Press, 1983.

 

Наверх

SQRTM - вычисление функции A ^1/2

Синтаксис:

             Y = sqrtm(A)
             [Y, esterr] = sqrtm(A)

Описание:

Функция Y = sqrtm(A) вычисляет одну из многих матриц, которые удовлетворяют условию Y * Y = A.

При таком обращении возможно появление диагностического предупреждения
             Warning: SQRTM appears inaccurate. esterr = xxx
             Предупреждение: функция SQRTM вычислена неточно. esterr = xxx

Если матрица A - действительная симметрическая или комплексная эрмитова, то теми же свойствами обладает и функция sqrtm(A).

Функция [Y, esterr] = sqrtm(A) кроме вычисленной матрицы возвращает оценку погрешности в виде относительной невязки

             norm(Y * Y - A) / norm(A).

В этом случае диагностическое сообщение не выводится.

Замечание:

Функцию sqrtm(A) не следует путать с функцией sqrt(A), которая вычисляет положительный квадратный корень от каждого элемента массива.

Примеры:

Рассмотрим матричное представление разностного оператора 4-го порядка.

         A =

	5	-4	1	0	0
	-4	6	-4	1	0
	1	-4	6	-4	1
	0	1	-4	6	-4
	0	0	1	-4	5

Эта матрица симметрическая и положительно определенная; ее единственный положительно определенный квадратный корень представляет собой разностный оператор 2-го порядка:

Y = sqrtm(A)
          Y =

	2.0000	-1.0000	0.0000	0.0000	0
	-1.0000	2.0000	-1.0000	0.0000	0.0000
	0.0000	-1.0000	2.0000	-1.0000	0.0000
	0.0000	0.0000	-1.0000	2.0000	-1.0000
	0.0000	0.0000	0.0000	-1.0000	2.0000

Матрица вида

X =

	7	10
	15	22

имеет 4 матрицы, являющиеся ее квадратным корнем.

Две из них следующие:

Две другие - соответственно -Y1 и -Y2.

Все 4 матрицы могут быть получены на основе спектрального разложения исходной матрицы

              [R, D] = eig(X).

 

 

Функция sqrtm строит решение только для положительных значений квадратных корней, и результатом является матрица Y1, хотя матрица Y2 представляется более предпочтительным решением, поскольку она целочисленна.

Алгоритм:

Функция sqrtm является просто аббревиатурой для вызова функции funm(A, ‘sqrt’). Алгоритм, реализующий функцию funm, использует приведение к форме Шура и может давать неточные или полностью несостоятельные результаты в случае кратных собственных значений.

Сопутствующие функции: EXPM, FUNM, LOGM.

 

Наверх

FUNM - вычисление произвольных функций от матрицы

Синтаксис:

Y = funm(A, ‘<имя функции>‘)
[Y, esterr] = funm(A, ‘<имя функции>‘)

Описание:

Функция Y = funm(A, ‘<имя функции>‘) позволяет вычислить любую функцию от матрицы, если она имеет имя, составленное из латинских букв. Это могут быть, например, все элементарные математические функции.

При таком обращении возможно появление диагностического предупреждения

            Warning: Result from FUNM may be inaccurate. esterr = xxx
            Предупреждение: Результат вычисления функции FUNM может быть неточным.esterr = xxx

Функция [Y, esterr] = logm(A) кроме вычисленной матрицы возвращает оценку погрешности в виде относительной невязки norm(expm(Y) - A) / norm(A).

В этом случае диагностическое сообщение не выводится.

Функции funm(A, ‘sqrt‘) и funm(A, ‘log‘) эквивалентны функциям sqrtm(A) и logm(A). Функции funm(A, ‘exp‘) и expm(A) вычисляют одну и ту же функцию, но различными способами; применение функции expm предпочтительнее.

Пример:

Следующие последовательности операторов в пределах ошибок округления должны давать одинаковые результаты.

	S = funm(A, ‘sin’);	E = expm(i * A);
	C = funm(A, ‘cos’);	C = real(E);
		S = imag(E);

В любом случае они удовлетворяют условию S*S + C*C = I, где I = eye(size(A)).

Алгоритм:

Функция funm вычисляется, функции от матриц с использованием алгоритма Парлетта [1-2]. Этот алгоритм потенциально неустойчив. Если матрица имеет кратные или близкие к ним собственные значения, то функция funm дает неточные или полностью несостоятельные результаты. При разработке алгоритма была сделана попытка выявить эту ситуацию и дать диагностическое сообщение. Однако выбранный критерий столь чувствителен, что сообщение может быть выдано даже при точном результате.

Если матрица A - действительная симметрическая или комплексная эрмитова, то ее форма Шура диагональна и результаты могут обладать очень высокой точностью.

Сопутствующие функции: EXPM, SQRTM, LOGM.

Ссылки:

1. Golub G. H., Van Loan. Matrix Computation. John Hopkins University Press, 1983.
2. Moler C. B., Van Loan. Nineteen Dubious Ways to Compute the Exponential of a Matrix//SIAM Review. Berlin, 1979. Vol. 20. P.801-836.

 

 

Полиномы и операции над ними

 

Наверх

POLYVAL - вычисление полинома

Синтаксис:

y = polyval(p, s)
Y = polyval(p, S)

Описание:

Функция  y = polyval(p, s), где p = [p₁ p₂ ... p_n p_n+1] - вектор коэффициентов полинома p(x) = p₁xⁿ + p₂x^n-1 + ... + p_nx + p_n+1, вычисляет значение этого полинома в точке x = s.

Функция Y = polyval(p, S), где S - одномерный или двумерный массив, вычисляет значение этого полинома для каждого элемента массива, поэтому size(Y) = size(V).

Пример:

Вычислим значение полинома p(x) = 3x² + 2x +1 в точке x = 5.

             p = [3    2   1]
             p = 3    2   1
             y = polyval(p, 5)
             y = 86

Сопутствующие функции: POLYDER, POLYVALM.

 

Наверх

POLYVALM - вычисление матричного полинома

Синтаксис:

             Y = polyval(p, S)

Описание:

Функция Y = polyval(p, S), где p = [p₁ p₂ ... p_n p_n+1] - вектор коэффициентов матричного полинома
            p(X) = p₁Xⁿ + p₂X^n-1 + ... + p_nX + p_n+1 ,
вычисляет значение этого полинома для матрицы X = S.

Пример:

Рассмотрим матрицу Паскаля порядка 4, составленную из биномиальных коэффициентов.

            S = pascal(4)
            S =

	1	1	1	1
	1	2	3	4
	1	3	6	10
	1	4	10	20

Вычислим характеристический полином этой матрицы.

p = poly(S)
p = 1.0000    -29.0000    72.0000    -29.0000     1.0000    3    2   1

Сравним результаты применения функций polyvalm и polyval.

polyvalm(p, S)	polyval(p, S)
1.0e-010 * -0.0027 -0.0094 -0.0222 -0.0428 -0.0094 -0.0326 -0.0749 -0.1423 -0.0222 -0.0749 -0.1713 -0.3233 -0.0428 -0.1423 -0.3233 -0.6091	16.00 16.00 16.00 16.00 16.00 15.00 -140.00 -563.00 16.00 -140.00 -2549.00 -12089.00 16.00 -563.00 -12089.00 -43779.00

Матрица polyvalm(p, S) в пределах погрешности - нулевая матрица, что подтверждает теорему Кэли - Гамильтона о том, что всякая матрица удовлетворяет своему характеристическому уравнению.

Матрица polyval(p, S) - это массив значений полинома p для каждого элемента матрицы S.

Сопутствующие функции: POLYDER, POLYVAL.

 

Наверх

CONV - умножение полиномов

Синтаксис:

             c = conv(a, b)

Описание:

Если заданы полиномы a и b длины степеней соответственно m и n, то их произведение - это полином c степени m + n, k-й элемент которого находится по формуле

.

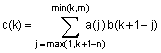Функция z = conv(x, y) вычисляет произведение двух полиномов a и b.

Пример:

Найдем произведение полиномов x³ + 2x² + 3x + 4 и 10x² + 20x + 30.

Для этого сформируем векторы a = [1 2 3 4] и b = [10 20 30] и вычислим

             c = conv(a, b)
             c = 10     40    100    160    170     120

Сопутствующие функции: DECONV, RESIDUE.

 

Наверх

DECONV - деление полиномов

Синтаксис:

[q, r] = deconv(c, a)

Описание:

Функция [q, r] = deconv(c, a) реализует деление полинома c на полином a; частное от деления возвращается в виде вектора q, остаток - в виде вектора r, так что выполняется соотношение c = conv(q, a) + r.

Пример:

Если c = [10 40 100 160 170 120] и a = [1 2 3 4], то деление этих полиномов дает следующий результат:

                [q, r] = deconv(c, a)
                q = 10    20    30
                r = 0    0    0    0    0     0,

и этот результат соответствует примеру из раздела CONV.

Сопутствующие функции: CONV.

 

Наверх

POLYDER - вычисление производных

Синтаксис:

            dp = polyder(p)
            dp = polyder(a, b)
            [q, p] = polyder(b, a)

Описание:

Функция dp = polyder(p) возвращает производную полинома dp(x) / dx.

Функция dp = polyder(a, b) возвращает производную от произведения полиномов a(x) * b(x).

Функция [q, p] = polyder(b, a) возвращает производную от отношения полиномов b(x)/a(x) в виде отношения полиномов q(x)/p(x).

Примеры:

Вычислим производную полинома p(x) = 3x² + 2x +1.

p = [3   2   1]; dp = polyder(p)
               dp =     6    2

Вычислим производную произведения полиномов.

a		b		dp = polyder(a, b)
1   3   5   7		3   2   1		15   44   66   68    19

Вычислим производную отношения двух полиномов b(x)/a(x).

b		a		[q, p] = polyder(b, a)
3   2   1		1   3   5   7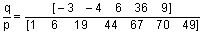

Сопутствующие функции: POLYVAL, POLYVALM.

 

Наверх

ROOTS - вычисление корней полиномов

Синтаксис:

r = roots(p)

Описание:

Функция r = roots(p), где p = [p₁ p₂ ... p_n p_n+1] - вектор-строка коэффициентов полинома p(x) = p₁xⁿ + p₂x^n-1 + ... + p_nx + p_n+1, вычисляет вектор-столбец корней этого полинома.

Функция p = poly(r), где r - вектор-столбец корней некоторого полинома, вычисляет вектор-строку коэффициентов этого полинома.

Пример:

Вычислим корни полинома p(x) = x³ + 3x² + 5x +7.

	p	r = roots(p)
	1   3   5   7	-2.1795 -0.4102 + 1.7445i -0.4102 - 1.7445I

p = poly(r)
p = 1.0000      3.0000     5.0000      7.0000 + 0.0000i

Сопутствующие функции: POLY.

 

Наверх

POLY - вычисление характеристического полинома

Синтаксис:

             p = poly(A)
             p = poly(r)

Описание:

Функция p = poly(A), где A - матрица порядка n, вычисляет вектор-строку коэффициентов характеристического полинома p(s) = det(sI - A) = p₁sⁿ + p₂s^n-1 + ... + p_ns + p_n+1.

Функция p = poly(r), где r - вектор-столбец корней некоторого полинома, вычисляет вектор-строку коэффициентов этого полинома.

Пример:

Рассмотрим рациональную матрицу А, вычисляя коэффициенты характеристического полинома, его корни и по ним вновь восстановим характеристический полином:

A =

	-5/3	-1	-2/3
	-5/6	1/4	11/12
	1/6	-17/4	-19/12

p = poly(A)
p = 1    3    5     7
r = roots(p)
r =    -2.1795
            -0.4102 + 1.7445i
            -0.4102 - 1.7445I
p = poly(r)
p = 1.0000    3.0000     5.0000    7.0000 + 0.0000i

Сопутствующие функции: ROOTS, RESIDUE.

 

Наверх

RESIDUE, RESI2 - разложение на простые дроби

Синтаксис:

[r, p, k] = residue(b, a)
coeff = resi2(u, v, pole, n, k)
[b, a] = residue(r, p, k)

Описание:

Функция p = [r, p, k] = residue(b, a) вычисляет вычеты, полюса и многочлен целой части отношения двух полиномов b(s) и a(s):

простые корни:

;

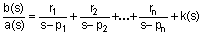• входные переменные - векторы b и a определяют коэффициенты полиномов числителя и знаменателя по убывающим степеням s;
• выходные переменные - вектор-столбец r вычетов, вектор-столбец p полюсов и вектор-строка k целой части дробно-рациональной функции;
• количество полюсов определяется по формуле:
  n = length(a) - 1 = length(r) = length(p);
• вектор коэффициентов многочлена прямой передачи будет пустым, если length(b) < length(a); в противном случае length(k) = length(b) -length(a) + 1;

кратные корни:

если p(j) = . . . =p(j+m-1) - полюс кратности m, то разложение на простые дроби включает член [1]

.

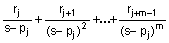Функция rj = resi2(b, a, pole, m, j) вычисляет вектор коэффициентов разложения дробно-рациональной функции b(s)/a(s) для полюса pole, имеющего кратность m. Параметр j указывает, какой из коэффициентов rj вычисляется при данном обращении к функции; по умолчанию j = m; если не указано m, то оно принимается за 1, то есть функция определяет вычеты для простых корней.

Функция [b, a] = residue(r, p, k) с тремя входными и двумя выходными параметрами выполняет обратную функцию свертки разложения в дробно-рациональную функцию отношения двух полиномов b(s) и a(s):

Пример 1:

Рассмотрим дробно-рациональную функцию отношения двух полиномов b(x)/a(x) с некратными корнями.

;
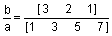[r, p, k] = residue(b, a)

r =	p =	k =
1.7642	-2.1795	[ ]
0.6179 + 0.7589i	-0.4102 + 1.7445i
0.6179 - 0.7589i	-0.4102 - 1.7445i

Поскольку порядок числителя меньше порядка знаменателя, целая часть функции отсутствует.

Пример 2:

Поменяем местами числитель и знаменатель дробно-рациональной функции.

;
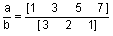          [ra, pa, ka] = residue(a, b)

ra =	pa =	ka =
0.5185 - 1.8332i	-0.3333 + 0.4714i	0.3333      0.7778
0.5185 + 1.8332i

В этом случае появляется целая часть функции, определяемая вектором ka.

Пример 3:

Обратимся к случаю кратных корней и рассмотрим следующую дробно-рациональную функцию:

;

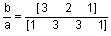r1 = resi2(b, a1, -1, 3, 1)	r2 = resi2(b, a1, -1, 3, 2)	r3 = resi2(b, a, -1, 3)
3	-4	2

Пример 4:

Обратимся к результатам примера 1. Зная их, восстановим исходную дробно-рациональную функцию, используя следующее обращение:

[b1, a1] = residue(r, p, k)

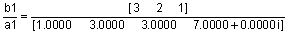
norm(a - a1) = 4.3739e-015

В пределах погрешности компьютера результаты совпадают.

Ограничения:

В вычислительном плане разложение дробно-рациональной функции на простые дроби плохо обусловлено. Если полином знаменателя имеет корни, близкие к кратным, то малые возмущения исходных данных могут привести к большим погрешностям вычисления полюсов и вычетов. Предпочтительнее использовать описание в пространстве состояний или представление таких функций в виде нулей и полюсов.

Сопутствующие функции: POLY, ROOTS.

Ссылки:

1. Oppenheim A. V., Schafer R. W. Digital Signal Processing. Prentice-Hall, 1975, P. 56-58.