Wavelet Toolbox - Очерк "Вокруг CWT"

Автор - К.А.Алексеев.

Теория вейвлет-функций, ворвавшаяся в мировую науку десятилетие назад и получившая самую широкую известность, проникла во многие области техники, экономику, финансы, завершила в них свой “инкубационный период” и в настоящее время продолжает стремительно увеличивать число своих приложений.

Содержание

1. Предисловие

2. Частотно-временная плоскость

3. Оконное преобразование Фурье

4. Вейвлет-функции

5. Рождение анализа

5.1. Взаимные корреляционные функции

5.2. Соотношение частота - масштабирующая переменная

Вейвлет-спектры

Обратное вейвлет-преобразование

8. Математический формализм

8.1. Прямое и обратное континуальное преобразования

8.2. Свойства континуального преобразования

8.2.1 Свойство линейности

8.2.2. Свойство инвариантности сдвигу

8.2.3. Свойство инвариантности к масштабированию

Равенство Парсеваля

Частотно-временные окна

11. Вейвлет-ряды

11.1. Кватование масштабирующей переменной

11.2. Квантование масштабирующей переменной и сдвига. Базис Рисса. Фреймы

Фильтрация сигналов

Приложение. Восстановление импульсных характеристик датчиков и испытательных воздействий с использованием континуального вейвлет-преобразования

Список литературы

 

Наверх

1. Предисловие

Теория вейвлет-функций, ворвавшаяся в мировую науку десятилетие назад и получившая самую широкую известность, проникла во многие области техники, экономику, финансы, завершила в них свой “инкубационный период” и в настоящее время продолжает стремительно увеличивать число своих приложений. 

Свидетельством революционного интереса к теории и практике вейвлет-анализа является лавинообразный поток издаваемой литературы. Например, в США, Германии и др. странах ежегодно издаются десятки книг, учебников и даже журналов, посвященных вейвлет-анализу, публикуются сотни статей, проводятся конференции. 

Так, достаточно упомянуть, что на Всемирном конгрессе математиков, проходившем в 1994 г. в Цюрихе, среди немногочисленных пленарных докладов, посвященных самым глубоким вопросам современной математики, И. Добеши (Daubechies, I.) был произнесен доклад о вейвлет-функциях, что, без преувеличения, явилось беспрецедентным событием для форумов подобного ранга (сплайны, некогда суперпопулярные, такой чести удостоены не были). 

В Интернете под редакцией В.Свелденса (Sweldens, W.) выходит электронный дайджест (“Wavelet Digest”), который публикует аннотации работ по вейвлет-функциям и их применению в математическом анализе, теории дифференциальных уравнений и т.д. 

Успехи теории вейвлет-функций до недавнего времени оставались полностью в руках математиков, определявших ее развитие и, собственно, публиковавших данные работы. Между тем, любая математическая теория может найти применение или, так сказать, материализоваться, только при условии, что ею овладеет масса инженеров, заключив ее в рамки технических приложений. Приходящее в последние годы понимание чисто математических вопросов теории привело к внедрению и использованию вейвлет-анализа в радиотехнике, связи, обработке и сжатии статических изображений и видео, анализе речи, распознавании образов, сейсмологии, гео- и астрофизике, анализе ЭКГ, энцефалограмм, томограмм и т.д. Об этом свидетельствует появление в научно-технической литературе также колоссального количества статей, посвященных именно инженерным приложениям вейвлет-функций. Правда, такое положение дел наблюдается опять-таки за рубежом: число публикаций, посвященных инженерным приложениям вейвлет-функций на русском языке, к сожалению, катастрофически мало. 

Проникновение вейвлет-анализа в область обработки сигналов можно считать естественным движением данной области от Фурье-анализа к методам, обеспечивающим частотно-временную локализацию сигналов. Дело в том, что анализ Фурье, как известно, обладает рядом недостатков, приводящих к потере информации о временных характеристиках сигналов и, как следствие, подразумевает использование искусственных приемов, направленных на установление их частотно-временной локализации (например, окон данных). Вейвлет-анализ оказался лишенным таких недостатков и, как следовало ожидать, проявил себя весьма аппликабельным к задачам, плохо поддающимся классическому анализу Фурье. 

В рамках обработки сигналов в настоящее время развит дискретный вейвлет-анализ, построены банки вейвлет-фильтров, заложены основы теории вейвлет-пакетов, целочисленного вейвлет-преобразования, лифтинг-схемы…

Однако на пути широкого и, что главное, оправданного применения вейвлет-функций к анализу данных существует также ряд препятствий, из которых главное представляет собой сложность математического аппарата.

 

Наверх

2. Частотно-временная плоскость

Свойство вейвлет-функций осуществлять частотную и временную локализацию сигналов достаточно просто продемонстрировать на плоскости, заданной в координатах частота – время. 

На данной плоскости вейвлет-функция может быть охарактеризована отрезком , равным ширине ее носителя, а также отрезком , имеющим ширину Фурье-образа функции. В этом случае изображение вейвлет-функции на частотно-временной плоскости имеет вид, показанный на рис. 1.

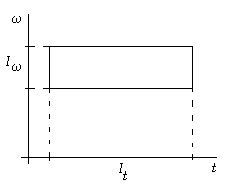
Рис. 1

Легко догадаться, что смещение вейвлет-функции на интервал  вызывает равное перемещение прямоугольника параллельно временной оси. С другой стороны, модуляция вейвлет-функции комплексной экспонентой  приводит на частотно-временной плоскости к сдвигу прямоугольника относительно оси частот на . Данное утверждение может быть доказано тем, что преобразование Фурье модулированной вейвлет-функции имеет вид:

,

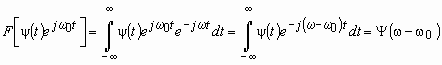где ,  – вейвлет-функция и ее Фурье-образ, смещенный в частотной области на . Результаты временной и частотной трансляций вейвлет-функции изображены на рис. 2.

Другое преобразование вейвлет-функции, такое как дилатация (сжатие или растяжение) приводит на частотно-временной плоскости к развороту частотно-временного прямоугольника. Так, например, сжимая вейвлет-функцию в  раз, получим новую функцию:

,

энергия которой после преобразования уменьшится в  раз:

.

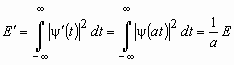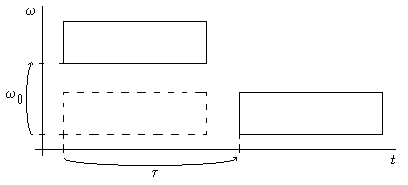
Рис. 2

Кроме того, поскольку при сжатии функции ширина ее носителя уменьшается в  раз, т.е. , ширина Фурье-образа в данном случае увеличивается в равное число раз: . Необходимо подчеркнуть, что подобное поведение вейвлет-функции и ее Фурье-образа согласуется с принципом неопределенности Гейзенберга, утверждающем, что увеличение ширины носителя функции во временной области приводит к уменьшению носителя ее образа Фурье, и наоборот. 

В качестве примеров, иллюстрирующих общие принципы представления функций на частотно-временной плоскости, рассмотрим -функцию Дирака и базис Фурье. 

Известно, что -функция Дирака является идеальным базисом для временного анализа континуальных сигналов, поскольку позволяет получить совокупность отсчетов сигнала (дискретизованный сигнал), рассматриваемых как временной спектр. На плоскости частота-время спектр -функции выглядит так, как показано на рис. 3. Из рисунка видно, что функция Дирака обладает свойством хорошей временной локализации, тогда как свойство частотной локализации у данной функции отсутствует (функция имеет плоский спектр). Действительно, образ Фурье -функции представляет собой константу и имеет вид:

.

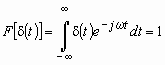В то же время, базисные функции Фурье, как раз наоборот обладают свойством хорошей частотной локализации, тогда как во времени имеют бесконечный носитель (см. рис. 4).

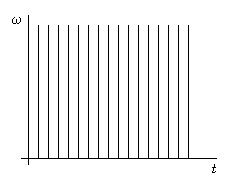Рис. 3

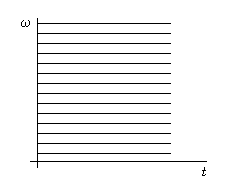Рис. 4

 

Наверх

3. Оконное преобразование Фурье

Недостаток анализа Фурье, обусловленный неспособностью осуществлять временную локализацию сингулярностей сигналов, может быть частично устранен путем введения в преобразование так называемого окна  – движущейся функции, имеющей компактный носитель. Использование оконной функции позволяет представить результат анализа – образ Фурье – в виде функции двух переменных, а именно частоты  и времени  положения окна:

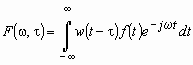, (1)

или с учетом обозначения

следующим образом:

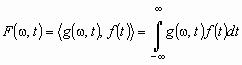. (2)

Проблема выбора оконной функции широко освещена в литературе [8 – 10, 12, 19] и, поскольку не является предметным вопросом настоящей лекции, более подробно здесь рассматриваться не будет. Однако представляется целесообразным повторно указать на тот факт, что введение оконной функции обеспечивает анализ Фурье техникой локализации сингулярностей по временной переменной.

На рис. 5 показана частотно-временная плоскость, на которой изображено оконное преобразование Фурье, соответствующее использованию ядра вида 

,

смещенного вдоль временной оси на интервал , а также различным значениям гармоник .

Из рисунка следует, что при сдвиге окна, осуществляемого вдоль временной оси, равно как при изменении частоты модуляции ширина частотно-временного прямоугольника остается неизменной. Данное обстоятельство объясняется тем фактом, что операция преобразования Фурье в данном случае осуществляется при постоянной ширине носителя оконной функции.

Одним из примеров оконного преобразования Фурье является преобразование Габора†, в котором роль оконной функции играет гауссиан. Преобразование Габора является одним из лучших оконных преобразований Фурье, поскольку обеспечивает наилучшую временную локализацию сигнала. 

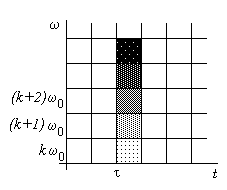
Рис. 5

Другими примерами оконных функций могут служить функции Хэмминга, Хэнинга, Кайзера, Бартлетта, Блэкмана, Чебышева и др., однако, как уже подчеркивалось, подробное изложение характеристик оконных функций, а также свойств анализа Фурье, приобретаемых вместе с введением оконной функции, достаточно легко найти в литературе, рекомендованной ранее.

 

Наверх

4. Вейвлет-функции

Вообще говоря, в литературе не существует единого определения вейвлет-функций; апеллируя, однако, к их свойствам, являющимся непосредственной ценностью в математических и инженерных приложениях, можно сказать, что, благодаря своей частотно-временной локализации, вейвлет-функции способны аппроксимировать т.н. “тонкую”, корреляционную, или нерегулярную, структуру сигналов.

Локализация вейвлет-функций во времени подразумевает наличие концентрации их энергии внутри некоторого финитного интервала, а также выполнение одного из законов их убывания [17]: 

, где ;

более быстро убывающего, чем ;

экспоненциального , где .

Частотная локализация вейвлет-функций говорит о компактности носителя их Фурье-образа, т.е. локализации его энергии внутри определенного частотного интервала. Существует, таким образом, аналогия между вейвлет-функциями и фильтрами, полоса пропускания которых определяется степенью гладкости самих функций во временной области и наличием некоторого числа нулевых моментов:

.

Кроме того, вейвлет-функции порождают базис Рисса [20], удовлетворяют концепции многомасштабного анализа, а также обеспечивают аппроксимацию данных с энтропией, меньшей исходной (при этом число вейвлет-функций, привлекаемых к аппроксимации, меньше числа исходных данных). 

Говоря о достоинствах вейвлет-функций, собранных вместе и положенных на одну чашу, нельзя забывать о том, насколько легки могут быть эти достоинства перед двумя перышками возражений, приводимых противниками вейвлет-анализа и положенными на другую чашу весов (именно так поступали египтяне, отыскивая в чем-либо истину). Первым из возражений является отсутствие у результата вейвлет-анализа какого-либо физического смысла: действительно, до сих пор представляется несколько затруднительной интерпретация вейвлет-спектра сигнала. Другое возражение представляет собой проблему высокой вариативности вейвлет-спектра от вида материнской вейвлет-функции (затронутые здесь вопросы являются предметом дальнейшего обсуждения).

Итак, свойство частотно-временной локализации является необходимым, но не достаточным условием выявления возмущений сигналов: для того, чтобы локализовать существующие сингулярности и при этом аппроксимировать ламинарное поведение сигналов представляется необходимым наличие набора вейвлет-функций, полученных посредством неоднократных трансляций и дилатаций одной, материнской, вейвлет-функции. 

Отметим, транслирование материнской функции представляет собой сдвиг функции вдоль временной оси на интервал , т.е. . 

Обеспечение частотной локализации, определяемой сжатиями и растяжениями материнской функции (дилатацией функции) осуществляется посредством введения другого аргумента – масштабного коэффициента , являющего собой аналог частоты анализа Фурье. 

В общем виде операция трансляции и дилатации материнской вейвлет-функции  могут быть записаны следующим образом:

, (3)

где .

Интересен тот факт, что масштабированию подвергается не только аргумент времени, но также переменная сдвига, что позволяет сохранить относительную плотность расположения синтезируемых вейвлет-функций во времени в случае расширения или сжатия материнской функции, т.е.  (см. рис. 6).

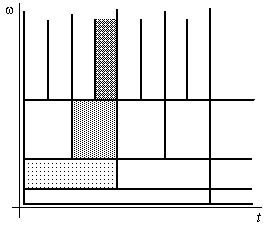
Рис. 6

Таким образом, наряду со свойством убывания по одному из упомянутых законов, вейвлет-функции должны удовлетворять следующим свойствам:

• ограниченность в пространстве 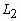, или квадратичная интегрируемость,
  ,
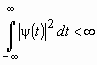  следуемая из того факта, что функции удовлетворяют какому-либо закону убывания;

• локализация, т.е. наличие компактного носителя как во временной, так и частотной областях определения функции;

• нулевое среднее, т.е. равенство нулю нулевого момента (площади вейвлет-функции),
  .

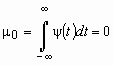В ряде случаев оказывается необходимым наличие также равенства нулю момента -го порядка, свидетельствующего о свойстве вейвлет-функций осуществлять анализ “тонкой” (высокочастотной) структуры сигнала, подавляя ламинарные (низкочастотные) составляющие,

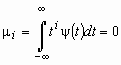. (4)

Приведем краткий список вейвлет-функций, удовлетворяющих вышеперечисленным условиям и получившим наибольшее распространение в задачах инженерного плана.

Прежде всего необходимо упомянуть вейвлет-функции, построенные на основе производных функции Гаусса, в общем случае записываемые следующим образом:

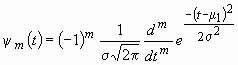, (5)

где  – первый начальный момент,  – среднеквадратическое отклонение. Отметим, при выполнении условия (4), очевидно, обеспечиваются равенства  и , в связи с чем общее выражение для вейвлет-функций (5) может быть переписано в виде:

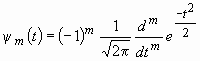. (6)

Так, первая производная функции Гаусса порождает WAVE-вейвлет, выражение для которого имеет вид:

.

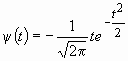Графическое изображение WAVE-функции представляет собой несимметричный вейвлет, нулевой момент которого (площадь под кривой) равен нулю (см. рис. 7).

Вторая производная функции Гаусса порождает вейвлет “сомбреро” (“мексиканская шляпа”), получивший данное название ввиду своей внешней схожести (см. рис. 8) с разрезом головного убора:

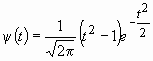. (7)

Необходимо отметить, что вейвлет “сомбреро” обладает двумя начальными моментами, равными нулю, в связи с чем его образ Фурье имеет меньшую по сравнению с WAVE-функцией ширину носителя и, следовательно, лучшую частотно-временную локализацию.

Разность двух гауссовых функций образует также DOG-вейвлет (от англ. – difference of gaussians):

,

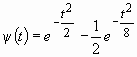график которого изображен на рис. 9.

Широкое распространение получил также вейвлет Морле:

 - (8)

в общем случае комплексная функция, вещественная и мнимая части которой суть гармоники доминирующей частоты , также модулированные гауссианом (см. рис. 10). (Присутствие доминирующей частоты в вейвлет-функции Морле позволяет варьировать избирательностью функции в частотной области.) 

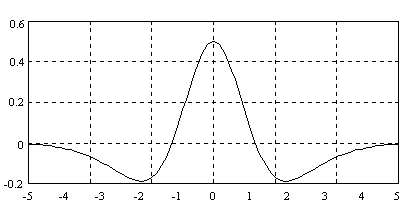Рис. 9

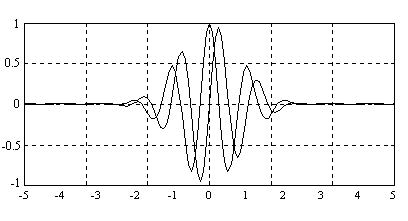Рис. 10

 

5. Рождение анализа

Наверх

5.1. Взаимные корреляционные функции

Континуальный вейвлет-анализ представляет собой достаточно гибкий и в то же время весьма мощный инструмент временного и спектрального анализа, целью которого является построение частотно-временных характеристик сигналов, во многом проясняющих природу не только сигналов в целом, но также их составляющих. Можно назвать по крайней мере 2 характерные особенности, присущие континуальному вейвлет-анализу.

Первой такой особенностью является трехмерное представление сигнала в спектральной области. Такое представление, вообще говоря, является избыточным и отдаленно напоминает изображение детали, узла механизма и т.д. на эпюре Монжа: эпюр не вносит в деталь каких-либо конструктивных изменений, однако, существенно увеличивает объем информации о ней. Кроме того, подобное представление обеспечивает необходимой информацией как о временных, так и спектральных сингулярностях сигнала.

Другой отличительной чертой является существование ряда возможностей уменьшения избыточности информации, приводящей к алгоритмам сжатия и выделения сигналов из шума, посредством введения техники статистического анализа. Здесь целесообразно подчеркнуть, что упомянутая гибкость вейвлет-анализа достигается посредством применения различных функций и, следовательно, процедур синтеза вейвлет-спектра сигнала и его сжатия. Подобная свобода выбора, очевидно, определяет результирующее качество анализа и поэтому представляет собой безусловное достоинство техники вейвлет-анализа.

Введение в вейвлет-анализ, на наш взгляд, целесообразно начать рассмотрением простейшего примера обработки чистого тона

(9)

с использованием, например, вейвлет-функции “сомбреро” (7). (Разумеется, Фурье-анализ в данном случае представляется более предпочтительным инструментом, однако анализ косинусоиды с помощью вейвлет-функции является всего лишь иллюстрацией).

Анализ косинусоиды осуществляется посредством трансляции вейвлет-функции вдоль временной оси с шагом , а также сравнением полученных временных клонов с отрезком косинусоиды, равным ширине носителя клона (см. рис. 11). По мере “продвижения” вейвлет-функции по косинусоидальному сигналу, очевидно, имеют место периодически повторяющиеся фазы наибольшего совпадения вейвлет-функции и косинусоиды, фазы меньшего совпадения, совпадения в противофазе, вновь меньшего совпадения и т.д. (Необходимо оговориться, что, простоты ради, здесь подразумевается равенство амплитуд косинусоиды и главного всплеска вейвлет-функции, а также равенство полупериода косинусоиды длине отрезка, соединяющего точки пересечения временной оси главным всплеском вейвлет-функции).

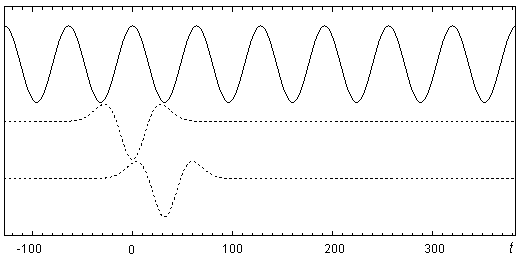
Рис. 11

Мера совпадения двух стационарных эргодических функций  и , одна из которых сдвигается относительно другой с шагом , может быть охарактеризована посредством корреляционной зависимости, имеющей, как известно, вид [8, 9, 19]:

,

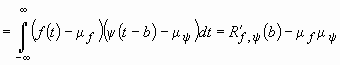где 

 –

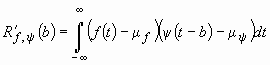взаимная ковариационная функция,  – первые начальные моменты функций  и  соответственно.

Поскольку по определению функции “сомбреро” , очевидно, что

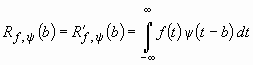, (10)

т.е. взаимная ковариационная функция и взаимная корреляционная функция равны.

В частном случае, при , взаимная корреляционная функция претерпевает вырождение в автокорреляционную функцию:

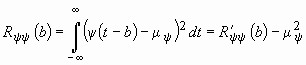
такую, что 

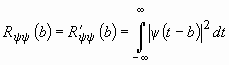(11)

при условии .

По определению автокорреляционная функция всегда является четной, т.е. имеет место равенство:

,

тогда как взаимная корреляционная функция свойством четности не обладает, удовлетворяя однако следующему соотношению:

.

Итак, поведение взаимной корреляционной функции, характеризующей меру совпадения косинусоиды и вейвлета, движущегося вдоль анализируемой гармоники, по-видимому, представляет собой также косинусоиду, взятую в противофазе (см. рис. 12). Здесь сплошной линией показана исходная гармоника (9), тогда как взаимная корреляционная функция (10) изображена пунктиром.

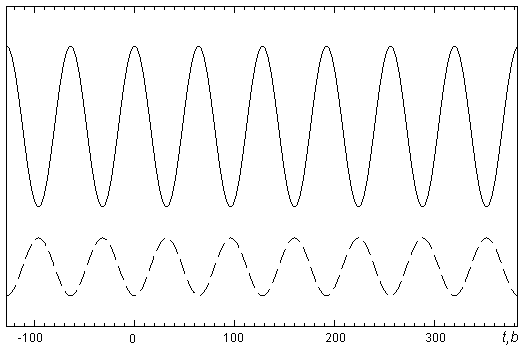
Рис. 12

Постепенно усложняя процесс обработки, осуществим дилатации материнской функции, т.е. ее растяжения и сжатия в  раз (3).

Однако здесь представляет интерес видимое поведение косинусоиды, амплитуда которой по мере сжатия вейвлет-функции будет стремиться к постоянной величине и, наоборот, содержать несколько полных периодов внутри носителя сильно растянутого вейвлета (см. рис. 13). В связи с этим оказывается совершенно естественным факт достижения взаимной корреляционной функцией, изображенной на данном рисунке пунктирной линией, наибольшей амплитуды при оптимальном соотношении “период косинусоиды – ширина носителя вейвлета” и ее минимального значения при предельном сжатии и растяжении вейвлет-функции.

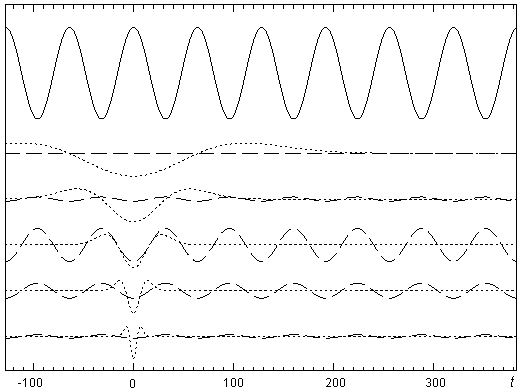
Рис. 13

Совокупность взаимных корреляционных функций, построенных для вейвлета “сомбреро”, взятого при различных значениях масштабирующей переменной , начиная с меньшего, и гармонического сигнала (9) приведена на рис. 14 и представляет собой результат континуального вейвлет-преобразования.

Подставив выражения для вейвлета “сомбреро” (7) и косинусоидального сигнала (9) в выражение для взаимной корреляционной функции (10), после интегрирования имеем:

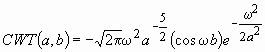, (12)

где  – результат континуального преобразования косинусоиды (от англ. – continuous wavelet transform),  – частота косинусоиды при  Гц.

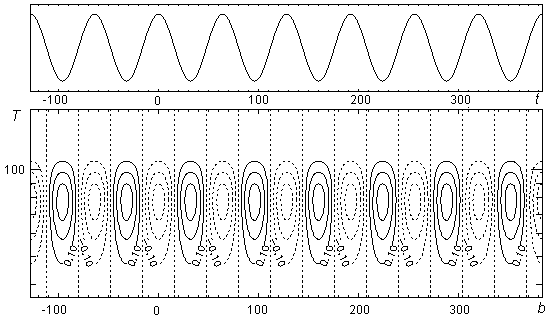
Рис. 14

Из рисунка следует, что результирующее преобразование  представляет собой функцию двух переменных: корреляционного сдвига  и масштабирующей переменной  материнской вейвлет-функции. Очевидно, максимумы и минимумы континуального преобразования, наблюдаемые на рис. 14, характеризуют местоположение всплесков косинусоиды, соответствующие выбору различных значений масштабирующей переменной вейвлета (об этом свидетельствует также присутствие некоторого числа контурных линий, сходящихся к вершине экстремумов).

Аналогичным образом найдем континуальное преобразование сигнала, представляющего собой суперпозицию трех гармонических составляющих (см. рис. 15), а также осциллирующего сигнала (развернутой синусоиды типа ), результат преобразования которого показан на рис. 16.

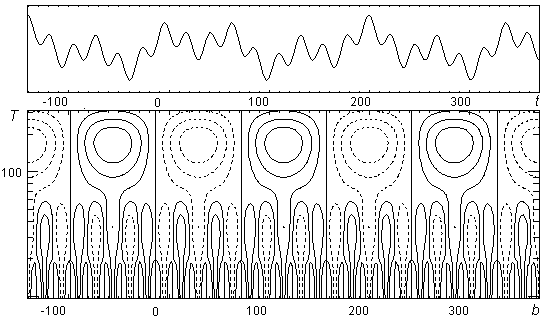
Рис. 15

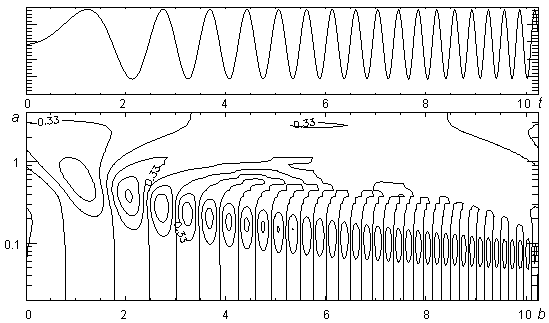
Рис. 16

При рассмотрении рис. 15 видно, что результирующая функция  содержит ярко выраженные экстремумы, соответствующие различным значениям масштабирующей переменной  и, следовательно, различным частотам, составляющим исследуемый полигармонический сигнал. В то же время достаточно просто обусловить тренд, наблюдаемый на рис. 16: уменьшение значения масштабирующей переменной вейвлета соответствует временной увеличению частоты нестационарного осциллирующего сигнала.

Другими примерами континуального преобразования нестационарных сигналов могут служить результаты преобразования амплитудно-модулированного сигнала (см. рис. 17), а также сигнала, представляющего собой частотно-временное распределение – совокупность гармоник, часть из которых взвешена шумом (см. рис. 18).

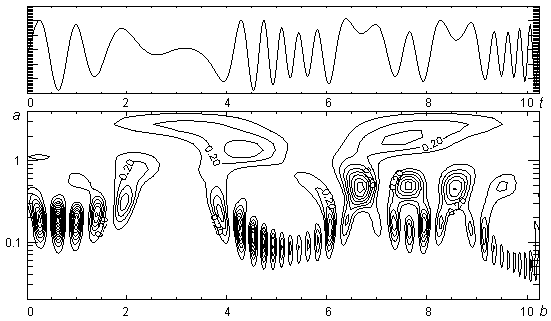
Рис. 17

Проиллюстрировать построение континуального анализа косинусоиды (9) можно также на примере wave-вейвлета

,

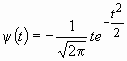изображенного на рис. 7. Подставляя выражение для данного вейвлета в выражение (10) для взаимной корреляционной функции, получим результат континуального преобразования косинусоиды в аналитическом виде:

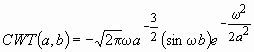. (13)

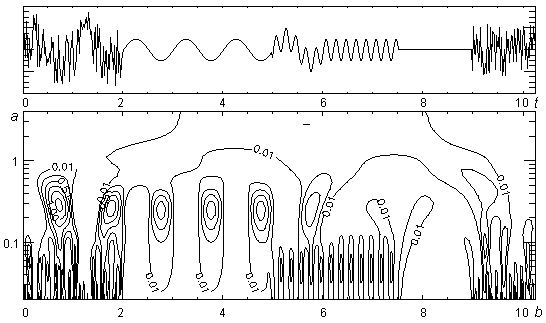
Рис. 18

Графическое изображение континуального преобразования (13) с помощью wave-функции, приведенное на рис. 19, показывает несколько худшую локализацию всплесков косинусоиды.

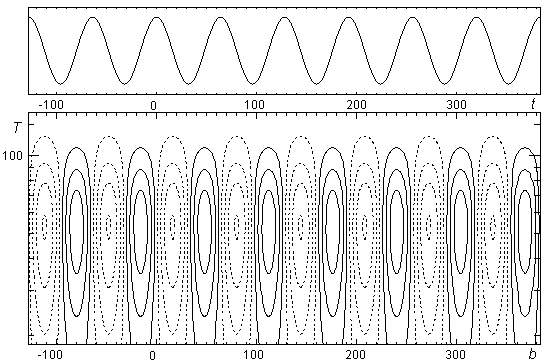
Рис. 19

Наверх

5.2. Соотношение частота - масштабирующая переменная

Как известно, одна из главнейших задач анализа сигналов суть задача идентификации частот гармонических составляющих. Данная задача является основополагающей также для континуального вейвлет-анализа, в связи с чем представляется целесообразным рассмотрение следующего вопроса.

Дело в том, что между концепцией комплексных гармоник Фурье и процедурой дилатации материнской вейвлет-функции существует некоторая, быть может, не совсем очевидная на первый взгляд взаимосвязь, позволяющая установить количественное соотношение между комплексной частотой Фурье и масштабирующей переменной вейвлет-функции. Необходимо подчеркнуть, что формальное соотношение, осуществляющее подобный пересчет, не является единственным: каждая вейвлет-функция обладает собственным коэффициентом пересчета. В этом можно убедиться, взглянув хотя бы на функции , соответствующие преобразованию одной и той же косинусоиды с помощью вейвлетов "wave" и "сомбреро" (см. рис. 14, 19).

Отметим, подбор коэффициента пересчета k осуществляется эмпирически посредством простого сравнения Фурье-образа гармоники, частота которой известна и равна , а также вейвлет-спектра той же гармоники:

.

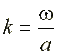Так, в настоящее время известны коэффициенты пересчета частот для вейвлета "сомбреро"

, (14)

wave-функции

(15)

и других.

Используя коэффициенты пересчета (14), (15), теперь достаточно просто идентифицировать частоту косинусоидального сигнала (9), предложенного для анализа в приведенных примерах.

 

Наверх

Вейвлет-спектры

По аналогии со спектральной плотностью Фурье  , характеризующей распределение энергии между гармоническими составляющими сигнала

, (16)

где 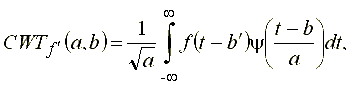 - его Фурье-образ, введем спектральную плотность сигнала  на плоскости вейвлет-преобразования:

. (17)

Здесь необходимо подчеркнуть, что вейвлет-спектры также обладают рядом поправочных коэффициентов, каждый из которых соответствует вейвлет-функции, используемой в качестве базиса преобразования. Например, поправочный коэффициент вейвлет-спектра, рассчитываемого в базисе функции "сомбреро" составляет .

Тогда общее выражение для спектра в базисе функции "сомбреро" имеет вид:

.

Следовательно, аналитическое выражение для вейвлет-спектра косинусоиды, полученное на основании функции (12) может быть записано как 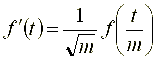(18)

(графическое изображение спектра приведено на рис. 20).

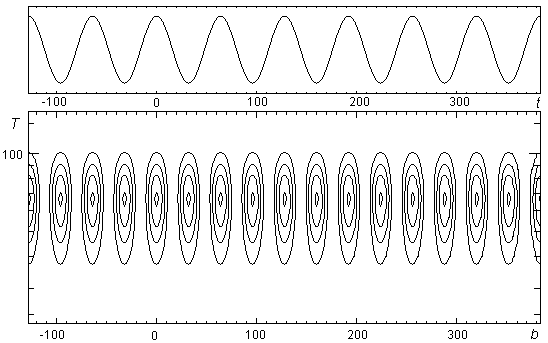
Рис. 20

Интегральная оценка вейвлет-спектра, полученная посредством интегрирования некоторой строки спектра, соответствующей какому-либо значению масштабирующей переменной вейвлет-функции, характеризует распределение энергии между сингулярностями сигнала, рассматриваемыми в масштабе :

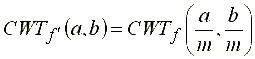(19)

На рис. 21 показана интегральная оценка спектра косинусоиды, рассчитанная в базисе функции "сомбреро". 

Ради полноты изложения следует отметить также, что оценка (19) вейвлет-спектров непериодических сигналов имеет вид, схожий со спектром Фурье.

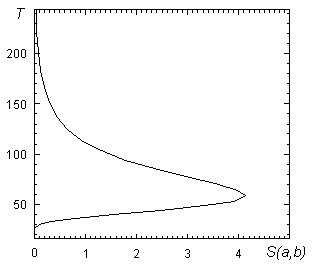
Рис. 21

 

Наверх

Обратное вейвлет-преобразование

Обратное вейвлет-преобразование, впрочем как и любое другое преобразование, соответствующее восстановлению сигнала по его спектральной функции, может быть определено как свертка функции  с вейвлет-функцией, используемой в качестве базиса преобразования.

На рис. 22 изображен исходный нестационарный сигнал, представляющий собой временное распределение гармоник, часть из которых взвешена шумом, функция  его континуального преобразования, а также сигнал, восстановленный по функции . В силу того факта, что вейвлет-функция в спектральной области образует полосовой фильтр, становится понятной причина сглаживания, наблюдаемого в первой и последней гармониках сигнала после операции его восстановления.

Выполнение обратного вейвлет-преобразования подразумевает необходимость расчета функции  для всех 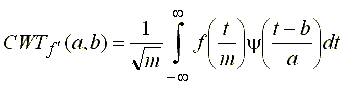 и 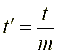, что, совершенно естественно, не представляется возможным на практике. С целью адаптации континуального вейвлет-преобразования к решению практических задач существуют процедуры квантования переменных масштаба и сдвига, правда, обусловливающие некоторые погрешности преобразования. Такие процедуры квантования и порождаемые ими фреймы рассмотрим после обращения к чисто формалистическим вопросам математики континуального преобразования.

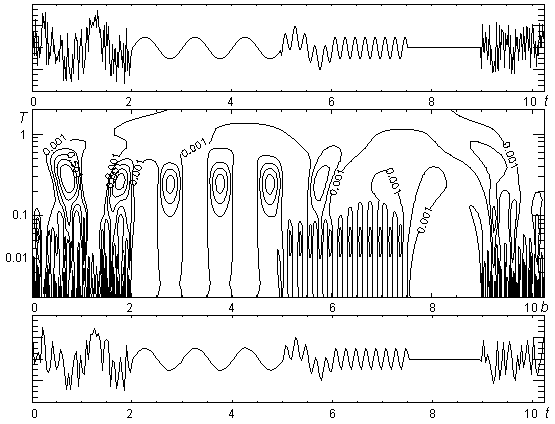
Рис. 22

 

8. Математический формализм

Наверх

8.1. Прямое и обратное континуальное преобразования

Введем в пространстве  базис, представляющий собой совокупность вейвлет-функций, порождаемых материнским вейвлетом  посредством его трансляций и дилатаций (3) и удовлетворяющих условиям, перечисленным в п. 4:

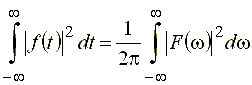, (20)

, .

На основании выражения (10), характеризующего взаимную корреляционную функцию исследуемого сигнала и базисной функции, запишем общее выражение для прямого континуального преобразования, осуществляемого над сигналом  в базисе (20):

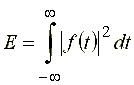
или в интегральной фoрме:

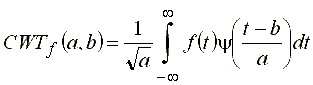. (21)

Тогда выражение для обратного преобразования может быть записано как свертка функции 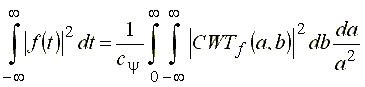 и базиса (20):

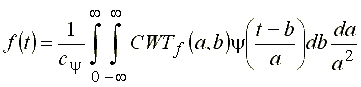. (22)

Здесь нормирующий коэффициент 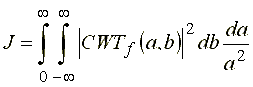, выражающий условие допустимости функций (20) в качестве базисных для пары преобразований (21), (22), имеет вид:

, (23)

где 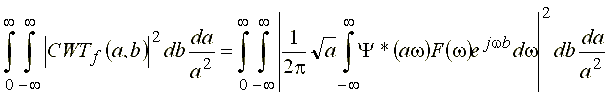 - Фурье-образ материнской вейвлет-функции.

Интегрируя данное выражение по частям, нетрудно убедиться, что условие  выполняется в том случае, если =0 при : ,

т.е. нулевой момент функции  также равен нулю.

Необходимо обратить внимание на тот факт, что выражение для обратного преобразования (22) представляет собой аналог тождества Кальдерона, о котором шла речь при рассмотрении истории разработок, имеющих природу вейвлет-анализа.

Из выражений, образующих пару континуальных преобразований (21), (22) видно, что обеспечение свойства частотно-временной локализации здесь достигается посредством использования ядра 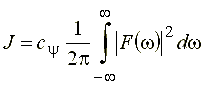, аналогичного ядру  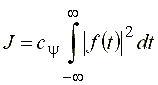преобразования Фурье, в котором роль частоты играет множитель , тогда как использование переменной сдвига  обеспечивает локализацию сингулярных структур сигнала во времени. Нормирующий коэффициент (23) обратного преобразования в анализе Фурье также имеет эквивалент, которым является множитель .

Найдем образ Фурье материнской вейвлет-функции (20), полагая, что :

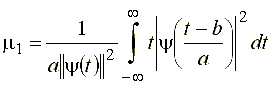(24)

Тогда выражение для прямого преобразования (21) в частотной области может быть записано следующим образом:

,

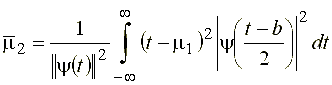где 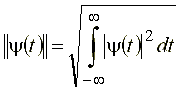 - образ Фурье анализируемого сигнала, * - знак комплексного сопряжения, или с учетом (24) в виде:

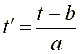. (25)

Отметим, аналог выражения (21) в частотной области может быть получен на основании равенства Парсеваля [8 - 10, 12, 13, 19].

Докажем, например, справедливость выражения (23), для чего в данном выражении рассмотрим интеграл

. (26)

Подставляя в выражение для 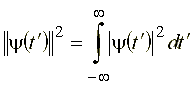 выражение (25), имеем:

.

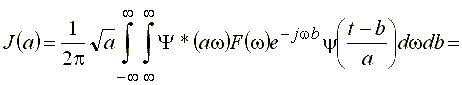
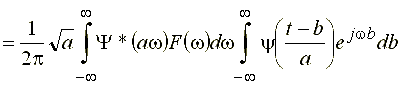Положим во тором интеграле, что 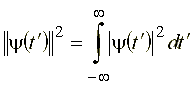, тогда, следовательно,

.

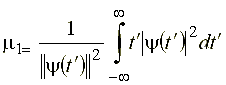После подстановки полученного выражения в интеграл , имеем выражение:

.

Данное выражение является подынтегральным выражением в (22):

. (28)

С другой стороны, второе подынтегральное выражение представляет собой обратное преобразование Фурье:

,

которое приводит (27) к виду:

.

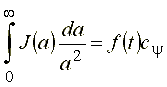Очевидно, полученные выражения в совокупности доказывают справедливость (22) как выражения для обратного преобразования:

,

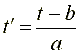что и требовалось доказать.

 

Наверх

8.2. Свойства континуального преобразования

Рассмотрим основные свойства континуального вейвлет-преобразования, а именно свойства линейности, инвариантности к сдвигу, инвариантности к масштабированию.

Наверх

8.2.1 Свойство линейности

Если , тогда

. (29)

На основании выражения (21) можно записать, что

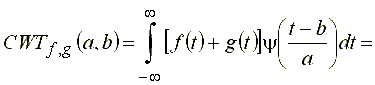
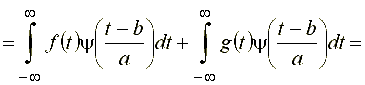
что и требовалось доказать.

Визуально данное свойство может быть доказано, например, с помощью средств пакета "Инструментарий элементарной волны" системы MatLab, как показано на рис. 23. Здесь на первом из рисунков показаны 2 синусоиды и их суперпозиция, на другом и третьем рисунках - вейвлет-преобразования составляющих бигармонического сигнала, тогда как на последнем - вейвлет-преобразование бигармонического сигнала в целом.

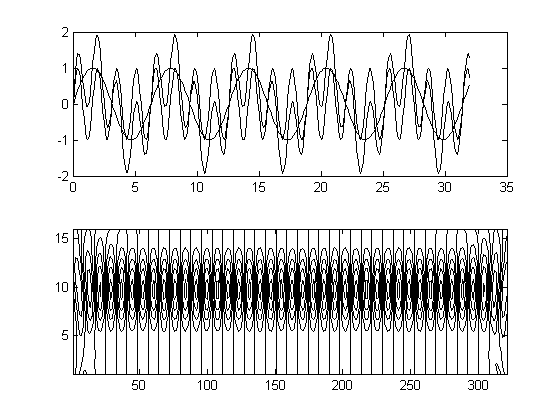
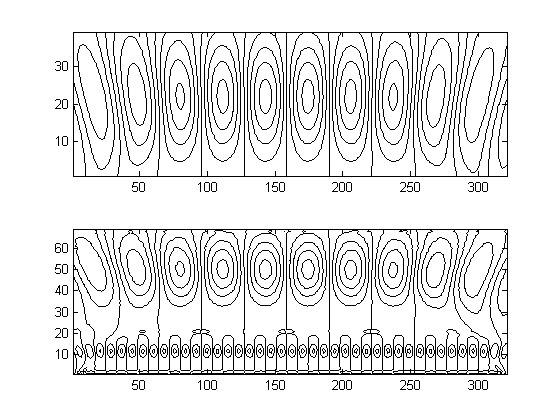
Рис. 23

 

Наверх

8.2.2. Свойство инвариантности сдвигу

Положим, сигнал  претерпевает сдвиг такой, что , тогда

. (30)

Поскольку общее выражение для прямого вейвлет-преобразования сигнала  имеет вид

то

,

где используемая подстановка .

Из данного выражения следует, что сдвиг сигнала вдоль временной оси на интервал порождает равный ему сдвиг вейвлет-образа (см. рис. 24).

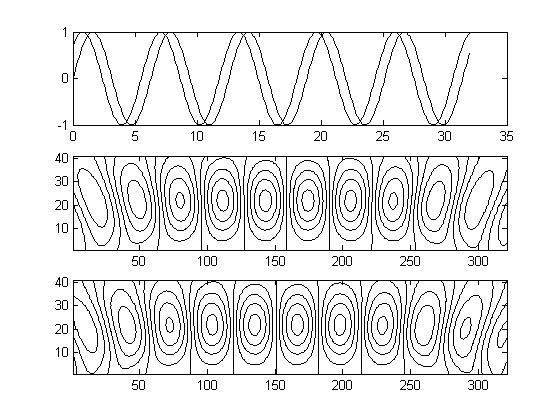
Рис. 24

 

Наверх

8.2.3. Свойство инвариантности к масштабированию

Положим, сигнал  претерпевает масштабирование в раз такое, что , причем энергия сигнала сохраняется (это следует из поправочного коэффициента ), причем

. (31)

Запишем аналогично предыдущему случаю выражение для прямого вейвлет-преобразования с учетом операции масштабирования сигнала:

.

Тогда, положив в подынтегральном выражении , получим:

.

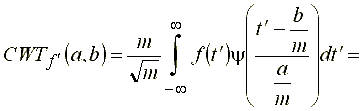
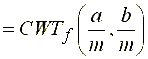Свойство инвариантности к масштабированию утверждает, что вейвлет-образ сигнала, подвергаемого масштабированию, также претерпевает масштабирующее преобразование: увеличение длины реализации сигнала во временной области приводит к расширению носителя его вейвлет-образа на плоскости (см. рис. 25).

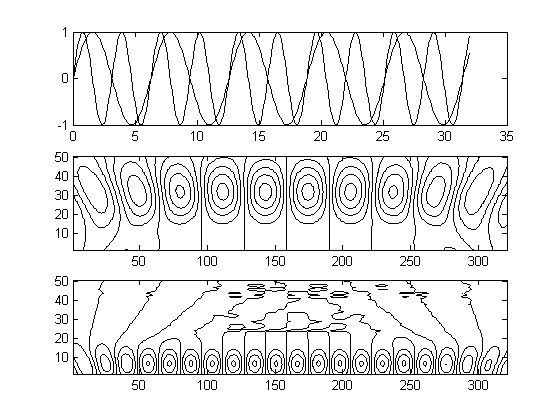
Рис. 25

 

Наверх

Равенство Парсеваля

Те, кто обладает здравым суждением, знают, 

какая существует разница между похожими словами

в зависимости от того, в каком месте

и при каких обстоятельствах 

эти слова употребляются. 

Б.Паскаль

Рассмотрим интерпретацию равенства Парсеваля, развитую в контексте континуального вейвлет-преобразования и причисляемую некоторыми авторами [21] к свойствам самого преобразования.

Как известно, равенство Парсеваля позволяет установить взаимосвязь между энергией сигнала, рассчитанной во временной области, и интегральной оценкой его спектральной плотности:

, (32)

Известно, что энергия сигнала может быть определена посредством расчета его автокорреляционной функции, отыскиваемой при нулевом временном сдвиге. Сказанное означает, что энергия сигнала в соответствие с выражением (11)

и является максимальным значением его автокорреляции:

. (33)

С другой стороны, согласно равенству Парсеваля, энергия сигнала, представленного на плоскости , может быть рассчитана как полная интегральная оценка его вейвлет-спектра, т.е.

. (34)

Для доказательства равенства Парсеваля на плоскости  рассмотрим правую часть выражения (34):

. (35)

Заменяя в данном выражении функцию  на выражение (25), получим:

.

Введем следующее обозначение:

и после подстановки его в полученное выражение дважды применим равенство Парсеваля, записанное в форме (32):

.

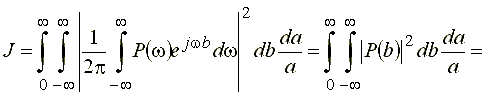
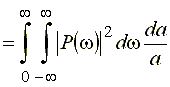Раскроем в полученном выражении подстановку (36), после чего запишем его следующим образом:

.

Очевидно, второй интеграл данного выражения представляет собой нормирующий коэффициент (28).

Таким образом, интеграл J, изначально записанный в форме (35), оказывается равен:

и, согласно равенству, следовательно,

, что и требовалось доказать.

 

Наверх

Частотно-временные окна

Когда бы я ни смотрел в окно, 

этот прямоугольник света рождает во мне целый мир мыслей.

Ж.Барбе Д'Оревильи,

"Дьявольщина"

Свойство частотной и временной локализации вейвлет-функций (20) может быть охарактеризовано концентрацией их энергии в частотной и временной областях, или посредством частотно-временных окон.

Построение частотно-временных окон основывается на определении вторых центральных моментов (дисперсии) функций  и , квадратный корень из которых как раз характеризует область наибольшей концентрации энергии.

Рассчитаем первый начальный (математическое ожидание) и второй центральный моменты функции следующим образом:

, (37)

, (38)

где  - норма базисной вейвлет-функции.

Тогда после замены переменной  и преобразований, связанных с ее введением под знак интеграла (37), получим:

.

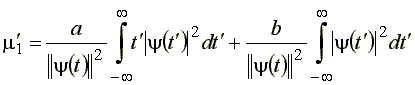Поскольку норма и энергия вейвлет-функции взаимосвязаны соотношением таким, что 

,

в то время как 

представляет собой первый начальный момент функции  (см. также выражение (37)), оказывается очевидным тот факт, что результирующее выражение для  принимает вид:

. (39)

Другими словами, всякая дилатация, осуществляемая над материнской вейвлет-функцией, приводит к пропорциональному увеличению расстояния между центрами тяжести ее клонов.

Подставим выражение (39) в выражение для второго центрального момента вейвлет-функции, в результате чего получим:

.

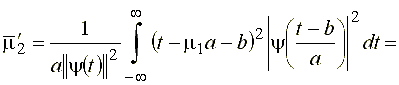
Введя в данном выражении обозначение , перепишем его в следующем виде:

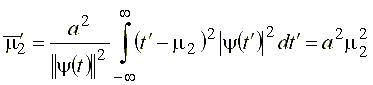. (40)

Выражение (40) определяет величину, представляющую собой квадрат диаметра вейвлет-функции, рассматриваемой во временной области. Сказанное означает, что вейвлет-функция занимает временное окно

(41)

а также обладает носителем

с центром в точке .

Можно сказать, что сингулярность сигнала , рассматриваемая в точке , может быть аппроксимирована с меньшей погрешностью при задании меньших значений масштабирующей переменной вейвлета, т.е. при попадании на плоскости  в так называемый угол влияния (см. рис. 26). В то же время, значение функции  в точке  может быть определено по значению сигнала , взятому в точке  при условии попадания в такой же угол (см. рис. 27).

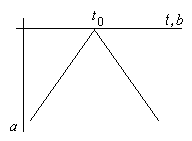
Рис. 26

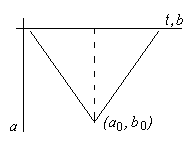
Рис. 27

Иначе говоря, мелкомасштабные сингулярности сигнала получают наилучшее отображение на плоскости  в случае задания малых значений переменной a вейвлет-функции, одновременно с этим претерпевая сглаживание при бoльших ее значениях, которые, в свою очередь, способствуют проявлению, как раз напротив, ламинарностей сигнала.

Определим аналогичным образом локальные свойства вейвлет-функции в частотной области, полагая, что представляет собой второй центральный момент образа Фурье  функции (20).

С целью записи континуального вейвлет-преобразования в частотной области воспользуемся нотацией Фурье, а также равенством Парсеваля (32):

,

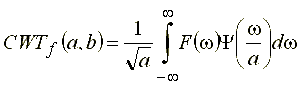т.е. констатируем тот факт, что вейвлет-преобразование представляет собой полосовой фильтр с настройкой  и шириной полосы пропускания  . Действительно, процедура дилатации, осуществляемая над вейвлет-функцией во временной области, соответствует обратному изменению ширины полосы пропускания фильтра в спектральной области: например, при уменьшении ширины носителя вейвлет-функции полоса пропускания фильтра увеличивается и наоборот.

Таким образом, можно сделать вывод о том, что вейвлет-преобразование обеспечивает информацией о спектре сигнала в полосе частот , т.е. в окне

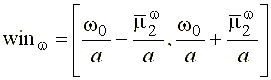, (42)

имеющем носитель

.

Набор фильтров с различной настройкой и шириной полосы пропускания, очевидно, позволяет судить о спектральном составе исследуемого сигнала во всем диапазоне анализа. При этом отношение центральной частоты настройки к ширине полосы пропускания 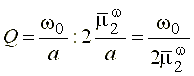, (43)

представляющее собой добротность фильтра, остается постоянным для любых значений масштабирующей переменной. Так, например, сдвиг настройки фильтра в сторону увеличения частоты приводит к расширению его полосы пропускания и наоборот, т.е. имеет место спектральный анализ сигналов с постоянной добротностью.

Свойство вейвлет-функций осуществлять спектральный анализ сигналов с постоянной добротностью, можно подтвердить также тем фактом, что площадь частотно-временного окна, занимаемого вейвлет-функцией, также остается неизменной для любых значений масштабирующей переменной и равной  (см. рис. 28). Действительно, данное свойство удовлетворяет принципу неопределенности Гейзенберга, утверждающему, что увеличение носителя вейвлет-функции во временной области приводит к уменьшению ее спектральной полосы и, наоборот, временное сжатие функции соответствует увеличению носителя ее образа Фурье.

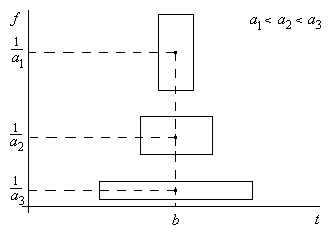
Рис.28

11. Вейвлет-ряды

Наверх

11.1. Кватование масштабирующей переменной

Как уже говорилось (см. п. 5), отображение сигнала на плоскости , полученное посредством континуального преобразования, является избыточным: во-первых, сигналы физического происхождения, например, отклики датчика, имеют конечную длину реализации, а, стало быть, ограниченную полосу частот, а во-вторых, результат преобразования (функция ) при определенных условиях решаемой задачи допускает наличие погрешностей анализа. Кроме того, процедура континуального преобразования, теоретически исполняемая для , очевидно, является нереализуемой на практике, в связи с чем возникает необходимость в использовании процедур квантования переменных ,  и, таким образом, перехода к процедуре представления сигналов с помощью рядов.

Наверх

11.2. Квантование масштабирующей переменной и сдвига. Базис Рисса. Фреймы

Рассмотрим случай квантования масштабирующей переменной вейвлет-функции, полагая, что правило квантования имеет вид:

, (44)

(это соответствует разбиению частотной оси на полосы). Предположим также, что настройка фильтра определяется так, что 

,

тогда как полоса его пропускания следующим образом:

.

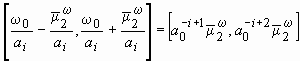Здесь необходимо отметить, что при ширине носителя частотного окна

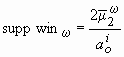
с одной стороны и

с другой, достаточно просто составить уравнение 

,

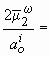
решением которого является .

Дело в том, что выбор масштабирующей переменной, равной 2, соответствует двукратному изменению частоты настройки фильтра и, таким образом, построению октавополосной фильтрации. (Для объяснения природы октавополосной фильтрации достаточно вспомнить диатоническую гамму, частоты первой и последней, восьмой, ступеней которой различаются в 2 раза).

Возвращаясь к теме обсуждения, можно показать, что вейвлет-функция (20) после процедуры квантования масштабирующей переменной, осуществляемой в соответствии с правилом (44), принимает вид:

. (45)

Тогда континуальное вейвлет-преобразование (21) сигнала может быть трансформировано к виду:

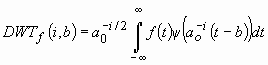, (46)

что представляет собой вейвлет-ряд (от англ. – discrete wavelet transform), составленный для квантованных значений масштабирующей переменной.

Однако в отличие от обратного континуального преобразования (22), на восстановление сигнала по значениям функции , а точнее, на базис (45) обратного преобразования необходимо наложить ограничения, выражающиеся в том, что образ Фурье вейвлет-функции (45) должен удовлетворять неравенству

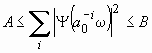, (47)

в котором А и В представляют константы

.

При этом условие (47) может быть истолковано следующим образом. Дело в том, что для каждого значения масштабирующей переменной вейвлет-функция в частотной области представляет собой полосовой фильтр, совокупность которых (банк фильтров) образует устройство, обладающее неравномерной частотной характеристикой (см. рис. 29). Степень неравномерности характеристики, очевидно, определяется константами А и В, образующими условие (47). Так, например, при сильной неравномерности характеристики сигнал на выходе банка фильтров претерпевает существенные искажения. Компенсация таких искажений составляет круг задач, которые могут быть решены с помощью так называемых дуальных фильтров, образ Фурье которых имеет вид:

.

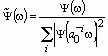В том случае, если вейвлет-функция (45), используемая в качестве базисной вейвлет-ряда, удовлетворяет условию (47), легко показать возможность полного восстановления сигнала по его вейвлет-ряду. Действительно, для всех

,

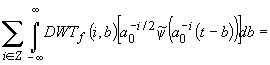
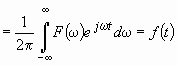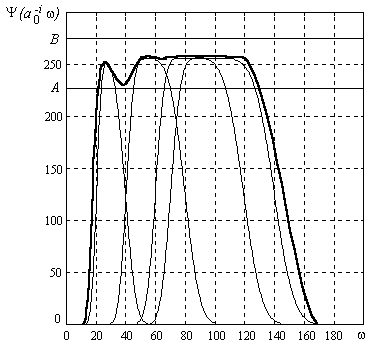
Рис. 29

поскольку 

,

где  – символ преобразования Фурье, причем

,

тогда как

в силу того обстоятельства, что  является дуальным фильтром для фильтра .

 

Наверх

Фильтрация сигналов

Одним из интересных инженерных приложений континуального анализа наряду с сжатием данных, является фильтрация.

В основе фильтрации сигналов, осуществляемой с помощью обратного континуального преобразования, лежит весьма простая и вместе с тем изящная идея разбиения вейвлет-спектра на полосы и использовании лишь тех из них, в которых имеет место наибольший объем информации о гармониках фильтруемого сигнала. Графически данную идею можно представить посредством отбрасывания каких-либо полос спектра, тогда как аналитически – заключением масштабирующей переменной  вейвлет-функции (см. выражение (52) для обратного преобразования в пределы, соответствующие границам используемой полосы.

На рис. 30 показан сигнал, первая и последняя гармоники которого зашумлены, его вейвлет-спектр, построенный в базисе функций Морле, а также сигнал, восстановленный по данному спектру, точнее его второй четверти (если считать сверху), отобранной для восстановления как наиболее информативной.

Вообще говоря, описанная процедура не является процедурой фильтрации в привычном смысле, однако может успешно применяться для решения задач фильтрации и шумоподавления.

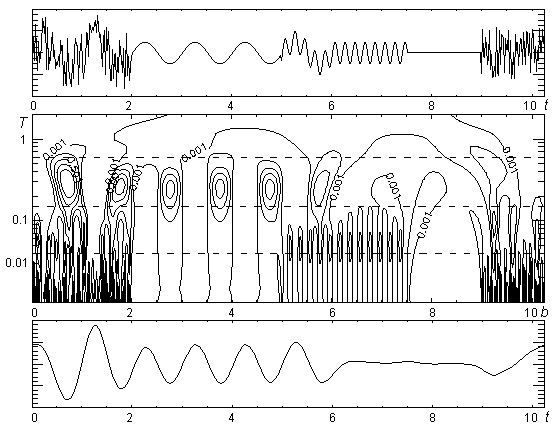
Рис. 30

 

Наверх

Приложение. Восстановление импульсных характеристик датчиков и испытательных воздействий с использованием континуального вейвлет-преобразования

Постановка задачи. Опыт разработки и эксплуатации датчиков переменных давлений [1 - 5] показывает, что частичное, а подчас полное отсутствие информации о динамике датчика в условиях эксплуатации объясняется недостаточностью знаний о его поведении в условиях аттестационных испытаний. Серьезной причиной возникновения данной проблемы является тот факт, что в настоящее время исполнение стендового оборудования в ряде случаев не отвечает требованиям, предъявляемым регламентом аттестационных испытаний. По большому счету, это выражается в невозможности воспроизведения идеальных испытательных воздействий, какими являются, например, ?-импульс, ступень, гармонический сигнал.

Так, приближение входного воздействия, аппроксимирующего ? -импульс, к идеальному посредством уменьшения длительности подразумевает увеличение его амплитуды, необходимое для введения датчика в режим свободных колебаний. Между тем, датчики обладают линейностью характеристик лишь в ограниченном диапазоне амплитуд входных воздействий, в связи с чем всякое превышение их мощности отражается в виде нелинейности типа насыщения.

В работах [6, 7] введено условие пригодности импульса давления в качестве испытательного воздействия, возникающего в условиях электрогидравлического эффекта (такой эффект наблюдается при взрыве металлического проводника в жидкой среде и используется для воспроизведения импульсов в стендовом оборудовании типа ИКД, ИКУ, ИДУ [7 – 9, 32]).

Данное условие утверждает следующее: в том случае, если длительность ? такого импульса, обладающего прямоугольной, треугольной, колоколообразной и т.п. формой, не превышает 0.3Т, где Т – период собственных колебаний датчика, импульс можно считать идеальным испытательным воздействием, тогда как отклик датчика рассматривать приближающимся к импульсной характеристике. 

Действительно, данное условие является методически корректным для датчиков, собственные частоты которых лежат внутри спектральной полосы воздействия (например, идентификация динамических характеристик датчиков, собственные частоты которых расположены внутри полосы 0 – 300 кГц возможна с погрешностью 3 – 15% при длительности импульса 3 мкс [8, 9]).

Некорректность задачи идентификации, обусловленная ненаблюдаемостью входа, т.е. отсутствием информации о временных характеристиках испытательного воздействия, позволила, тем не менее, разработать ряд методик идентификации динамических характеристик датчиков по их откликам на испытательное воздействие типа ?-импульса. В частности, публикации [10 - 13] содержат описания способов, основанных на анализе Фурье и нацеленных на обработку коротких реализаций откликов, а также параметрических методов, в которых предполагается выбор участка (участков) отклика, обладающих наивысшим значением отношения сигнал/шум. Кроме того, наряду с выбором участка отклика упомянутые методики предполагают также отбрасывание его первого полупериода, т.е.  первых отсчетов, содержащих вынуждающую составляющую и свободные колебания датчика, и, вместе с тем, последний полупериод как наиболее зашумленную часть отклика. Таким образом, число оставшихся целых периодов отклика должно обеспечивать минимальное значение методической погрешности идентификации [13]. 

Между тем, ограничение длины реализации, как известно, сопровождается проявлением ряда недостатков, среди которых наиболее существенным является ухудшение спектрального разрешения и утечка в спектральной области. (Вспомним полноты ради, что взаимосвязь входного воздействия и отклика может быть определена интегралом фредгольмова типа в пределах ).

Широкополосность датчиков переменных давлений новых поколений не позволяет считать упомянутое условие приемлемым с точки зрения удовлетворения частотного диапазона испытания. Очевидно, в данном случае задача идентификации динамических характеристик сводится к более общей задаче, смысл которой заключается в определении характеристик по входному воздействию известной формы [14 - 17]. Однако такая задача включает в себя проблему выделения импульсной характеристики датчика и испытательного воздействия из отклика.

Как известно, сигналы физического происхождения имеют конечную длину реализации и занимают ограниченную полосу частот. В связи с этим представляется совершенно естественным тот факт, что континуальное вейвлет-преобразование, теоретически исполняемое для , ,  является нереализуемым на практике, а потому подразумевает необходимость квантования переменных .

Квантование масштаба преобразования может осуществляться двумя способами, из которых первый, наиболее очевидный, заключается в использовании правила , где , тогда как второй, инженерный, основывается на следующих соображениях. 

Поскольку масштабирующая переменная вейвлет-функции и ее центральная частота, а точнее настройка фильтра, порождаемого вейвлет-функцией, обратно пропорциональны друг другу, имеет смысл задание интервала изменения масштабирующей переменной, обусловленного предельными низкочастотной и высокочастотной составляющими анализируемого сигнала:

. (1)

Здесь  – шаг приращения масштабирующей переменной, А – количество таких приращений.

Квантование переменной сдвига, на наш взгляд, целесообразно осуществлять в предположении равенства шага ее приращения шагу дискретизации сигнала:

, (2)

где – число отсчетов сигнала.

Тогда выражение для континуального вейвлет-преобразования 

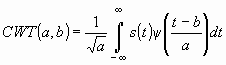
может быть переписано следующим образом:

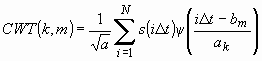
или с учетом правил (1), (2) квантования переменных  в виде:

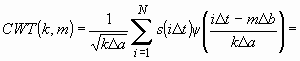
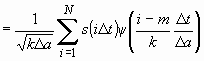. (3)

Обратное вейвлет-преобразование, соответствующее восстановлению сигнала по его спектральной функции, может быть определено как внутреннее произведение  с вейвлет-функцией, используемой в качестве базиса:

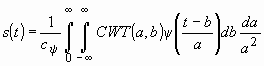, (4)

где .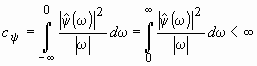

Как видно, выполнение обратного вейвлет-преобразования подразумевает необходимость интегрирования произведения  и  в пределах ,  что, совершенно естественно, также не представляется целесообразным на практике. В связи с этим правила квантования масштаба и сдвига могут быть применены также к процедуре обратного вейвлет-преобразования, общее выражение для которого примет вид:

.

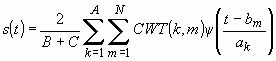Здесь  представляют собой константы Рисса [18-20]. 

В частности, для ортонормированного базиса, в котором , выражение записывается следующим образом:

.

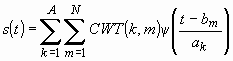Очевидно, выражение для практической реализации обратного вейвлет-преобразования с учетом правил (1), (2) принимает вид:

.

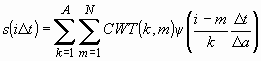В основе алгоритма восстановления импульсных характеристик датчиков и испытательного воздействия с использованием обратного вейвлет-преобразования лежит весьма простая идея разбиения вейвлет-спектра отклика на полосы и использования лишь тех из них, в которых заключен наибольший объем информации об искомых составляющих. Говоря иначе, в том случае, если наибольшая концентрация энергии вейвлет-спектра импульсной характеристики соответствует полосе , ее можно восстановить по функции , взяв таким образом, что :

. 

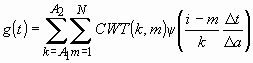Аналогичным образом, зная ширину полосы вейвлет-спектра испытательного воздействия, его достаточно просто восстановить в предположении, что :

.

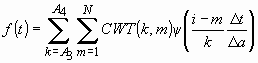Некоторые результаты и их интерпретация. На рис. 1 – 4 изображены отклики датчиков переменных давлений, полученные методом активной импульсной идентификации на стенде ИКД-7; вейвлет-спектры откликов, рассчитанные с использованием биортогональных сплайновых вейвлет-функций порядков (6,8), а также испытательные воздействия и импульсные характеристики датчиков, восстановленные по данным вейвлет-спектрам.

При рассмотрении рисунков видно, что спектры окликов датчиков содержат 2 составляющие, из которых одна соответствует спектру импульсной характеристики, проявляющейся в виде ряда локальных максимумов, тогда как другая – спектру испытательного воздействия, лежащего в более высокочастотной области (спектр испытательного воздействия выделен прямоугольником).

Можно заметить, что спектры испытательных воздействий не имеют длительности, равной первому полупериоду отклика датчика. Очевидно, степень проявления вынуждающей составляющей в отклике определяется полосой пропускания аттестуемого датчика.

Стоит отметить, что наибольшим сюрпризом в решении поставленной задачи явилась не столько возможность быстрого восстановления импульсной характеристики и испытательного воздействия, каковую обеспечил вейвлет-анализ, сколько форма вынуждающей составляющей: рис. 1 – 4 убедительно иллюстрируют тот факт, что испытательное воздействие вовсе не является одиночным импульсным! Напротив, будучи синтезированным посредством взрыва проводника в жидкой среде, воздействие представляет собой ни что иное, как серию или, можно сказать, пакет импульсов, порождаемых процессами, протекающими в камере стенда в течение эволюции электрогидравлического эффекта. При этом весьма важным является то обстоятельство, что полученные результаты в полной мере согласуются с представлениями о физике эффекта, развитыми в работах [22-33] и в их свете могут быть интерпретированы следующим образом. 

Диспергирование продуктов взрыва проводника, т.е. взрывообразное расширение облака, наполненного продуктами взрыва, приводит к тому, что на границе раздела сред облако – жидкость образуется зона повышенного давления, обусловленного сжатием близлежащих слоев жидкости. Сказанное означает, что в жидкости образуется фронт ударной волны, по обеим сторонам которого давление, скорость и плотность претерпевают разрыв [25, 26]. Под воздействием давления падающей волны приводится в движение упругая система датчика, т.е. имеет место процесс импульсного нагружения. Таким образом, развитие в импульсной камере ударной волны соответствует импульсу, первому из пакета импульсов испытательного воздействия.

Падение волны на внутреннюю поверхность камеры приводит к возникновению сложной системы отраженных волн, в совокупности образующих сходящиеся движения жидкости [22]. Понятно, результатом возникновения отраженных волн для датчика является разгружение его упругой системы [28].

Взаимодействие “хвоста” прямой и отраженной волн друг с другом приводит к зарождению кавитационной зоны, локализующейся у внутренней поверхности камеры. Опуская подробности, характеризующие условия рождения кавитации и физику ее эволюции (подробнее об этом см., например, в [22-24, 31]), скажем следующее. Кавитационная зона, фактически “выстилающая” внутреннюю поверхность камеры, под воздействием результирующего давления начинает совершать объемные колебания, напоминающие пульсации газового пузыря [27, 29, 31, 33] и порождающие серию импульсов, отчетливо видимых на графике испытательного воздействия. Действительно, в момент образования зоны кавитации непосредственное воздействие падающей ударной волны на упругую систему датчика прекращается. Теперь волна оказывает лишь косвенное влияние на процесс нагружения, ударяясь хвостовой частью о кавитационную зону.

Отражение хвоста ударной волны от зоны кавитации протекает в условиях электрогидравлического эффекта подобно явлению отражения от упругой поверхности [33]. Дело в том, что недостающее давление в хвосте ударной волны не позволяет подавить кавитацию, а способно привести лишь к зарождению дополнительной кавитационной зоны [28, 31]. Нетрудно догадаться, что ее поведение влияет на динамику упругой системы датчика также косвенно.

Образование зон первичной и вторичной кавитации наводит на мысль о вероятном переходе всего объема жидкости в кавитирующее состояние. Подобное состояние можно охарактеризовать наличием в среде как крупных зон кавитации, создающих биения низкой частоты, так и зон меньших объемов, частоты биения которых выше. Можно сказать, жидкость теперь представляет собой единую осциллирующую суперкаваерну, размеры которой определяются размерами импульсной камеры. Отметим, жизнедеятельности и гибели суперкаверны соответствует ряд импульсов из пакета импульсов испытательного воздействия, а также отдельные всплески и шум его второй половины [23].

Дополнительные замечания. Обратимся вновь к рассмотрению рис. 1 – 4 для того, чтобы сделать ряд дополнительных замечаний и охарактеризовать поведение датчиков более подробно.

В частности, после отработки первого импульса на вход широкополосного датчика ЛХ612 №74942184 подается другой импульс, достигающий своего максимума в момент времени 0,9 мкс (см. рис. 1). Реакция датчика на данное воздействие также представляет собой импульс, максимум которого наблюдается с запаздыванием, равным примерно 0,3 мкс. Третий входной импульс (его максимум соответствует времени 1,9 мкс), четвертый (3,3 мкс) и пятый (4,3 мкс) импульсы отрабатываются датчиков с тем же запаздыванием. Примечателен также тот факт, что разнесение импульсов во времени позволяет датчику достичь режима свободных колебаний.

Аналогичным образом можно охарактеризовать поведение датчика ДПС010 №907 (см. рис. 2). Здесь, однако, стоит обратить внимание на то, что входной пакет импульсов датчик “фильтрует” подобно конденсаторному мосту выпрямителя. Очевидно, частота следования импульсов пакета превышает частотный диапазон данного датчика. Напротив, одиночные импульсы, наблюдаемые в моменты 2,8; 4,0; 5,7 и 6,9 мкс соответственно, удовлетворительно отрабатываются датчиком с запаздыванием, равным примерно 0,3 мкс.

Описанная выше ситуация наблюдается также в реакции датчика ДПС008 №2183 (см. рис. 3) на пакет входных импульсов испытательного воздействия.

Отклик датчика ЛХ612М №830182, его импульсная характеристика и испытательное воздействие, изображенные на рис. 4, вообще примечательны. Как видно, испытательное воздействие, поданное на вход датчика, представляет собой слабо затухающую серию импульсов, напоминающую стохастический сигнал. Реакция датчика на подобное воздействие представляется вполне очевидной: таковой являются два колебания, наблюдаемые в моменты времени 0,3 и 3,8 мкс соответственно.

Отметим, по осям абсцисс рассматриваемых графиков отложены номера отсчетов сигналов.

Заключение. В настоящем приложении рассмотрено решение проблемы восстановления импульсных характеристик датчиков переменных давлений и испытательных воздействий, синтезируемых взрывом металлического проводника в жидкой среде. Как видно, аппарат континуального вейвлет-анализа позволил доказать гипотезу, согласно которой испытательное воздействие представляет собой пакет импульсов. В то же время, проведенный расчет частных динамических характеристик датчиков натолкнул на мысль о том, что аппарат континуального анализа может быть с успехом применен в задачах параметрической идентификации средств измерений, а также фильтрации измерительной информации.

Литература

1. Коптев Ю.Н., Гориш А.В. Датчиковая аппаратура для ракетно-космической техники // Радиотехника, 1995, №10. – С.5-6

2. Мокров Е.А. О тенденциях развития датчиков специального назначения // Приборы и системы управления, 1990, №10. – С. 4-5

3. Бутов В.И., Забродина С.Д., Кузин В.Н. Пьезоэлектрические датчики быстропеременных давлений // Приборы и системы управления, 1990, №10. – С. 11-12

4. Михайлов П.Г., Бутов В.И., Политменцева Т.Н., Гориш А.В. Пьезодатчики быстропеременных, импульсных и акустических давлений // Радиотехника, 1995, №10. – С.36-37

5. Казарян А.А. Обзор датчиков пульсаций давления // Измерительная техника, 1998, № 8. – С.27-33

6. Багдатьев Е.Е., Ефимова А.А. Идентификация преобразователей переменных давлений // Измерительная техника, 1986, №6. – С. 17-18

7. Багдатьев Е.Е., Ефимова А.А., Санина Э.Б. Импульсная установка для идентификации датчиков переменных давлений // Измерительная техника, 1989, №3. – С. 18-19

8. Кузнецов Е.А. Автоматизированный комплекс для определения статико-динамических характеристик датчиков давления в широком диапазоне температур // Измерительная техника, 1993, №6. – С. 40-43

9. Кузнецов Е.А. Методы и средства оценки динамических характеристик датчиков давления при криогенных и повышенных температурах // Автореф. дисс. ... канд. техн. наук. – Москва, 1997

10. Мясникова Н.В., Строганов М.П. Методы определения динамических характеристик датчиков механических величин. – Пенза: Изд-во Пенз. политехн. ин-та, 1991. – 60 с.

11. Мясникова Н.В., Иосифов В.П., Строганов М.П. Оценивание частотных характеристик датчиков механических величин по результатам прямых измерений // Датчики систем измерения, контроля и управления: Межвуз. сб. науч. тр. – Пенза: Изд-во Пенз. гос. техн. ун-та, 1991. – Вып. 13. – С. 88-91

12. Мясникова Н.В. Применение метода Прони для идентификации характеристик датчиков переменных давлений // Датчики систем измерения, контроля и управления: Межвуз. сб. науч. тр. – Пенза: Изд-во Пенз. гос. техн. ун-та, 1989. – Вып. 9. – С. 86

13. Мясникова Н.В. Оценка погрешностей при идентификации динамических характеристик средств измерения // Датчики систем измерения, контроля и управления: Межвуз. сб. науч. тр. – Пенза: Изд-во Пенз. гос. техн. ун-та, 1988. – Вып. 8. – С. 86-89

14. Алексеев К.А. Идентификация динамических характеристик датчиков с помощью детерминированного импульса давления // В кн. “Измерения, автоматизация и моделирование в промышленности и научных исследованиях”, 1-ая Всеросс. научно-практ. конф., Бийск, 2000. – С. 217-22

15. Алексеев К.А. Задача идентификации полных и частных динамических характеристик высокочастотных пьезоэлектрических датчиков переменных давлений // Приборы и системы. Управление, контроль, диагностика, 2000, №7. – С. 58-61

16. Осадчий Е.П., Алексеев К.А. Идентификация импульсных характеристик датчиков переменных давлений с использованием матриц двумерных нестационарных передаточных функций //Датчики и системы, 1999, №6.–С.16-19

17. Алексеев К.А., Алексеева М.Б. Идентификация динамических характеристик датчиков в базисе функций Уолша // Информационно-измерительная техника: Межвуз. сб. науч. тр. – Пенза: Пенз. гос. ун-т, 2000. – Вып. 25. – С. 62-70

18. Алексеев К.А. Вейвлет-анализ сигналов датчиков. Часть 1. Континуальный вейвлет-анализ // Пенза: ИИЦ ПГУ, 2001. – 60 с.

19. Истомина Т.В., Чувыкин Б.В., Щеголев В.Е. Применение теории wavelets в задачах обработки информации. – Пенза: Изд-во Пенз. гос. ун-та, 2000. – 188 с.

20. Новиков И.Я., Стечкин С.Б. Основы теории всплесков // Успехи математических наук, 1998, №6. – С. 53 – 128

21. Новиков Л.В. Основы вейвлет-анализа сигналов. – СПб., 1999. – 152 с.

22. Алексеев К.А., Осадчий Е.П. Исследование электрогидравлического эффекта, воспроизводимого в импульсной камере стенда ИКД-5, и моделей его компонент // Инженерная физика, 2000, №2. – С.16-24

23. Алексеев К.А. Возникновение кавитационных явлений в условиях электрогидравлического эффекта и их роль в процессе импульсной идентификации // Материалы Междунар. науч.-техн. конф. “Методы и средства измерения в системах контроля и управления”. – Пенза, 1999. – С. 97-99

24. Алексеев К.А. Определение спектральной плотности пульсаций давления // Тез. докл. Междунар. симпозиума “Надежность и качество-99. Инновационные технологии производству ХХI века”. – Пенза, 1999. – С. 250-252

25. Alexeev C. A simulation of the shock wave synthesized in water by an exploding wire // Proc. of the Inter. Symp. “Reliability and Quality 2000”, Penza, 2000

26. Alexeev C. A movie-representation of the electro-hydraulic effect // Proc. of the Inter. Symp. “Reliability and Quality 2000”, Penza, 2000

27. Бескаравайный Н.М., Поздеев В.А. Волновые задачи о расширении полости в жидкости с учетом конечности перемещения границ // Физико-механические процессы при высоковольтном разряде в жидкости: Сб. науч. тр. – Киев: Наук. думка, 1980. – 220 с.

28. Гаманович В.И., Стрельцов В.А. Взаимодействие ударной волны с преградой конечной толщины // Электрический разряд в жидкости и его применение: Сб. науч. тр. – Киев: Наук. думка, 1977. – 176 с.

29. Демина В.М., Шкатов А.А. Исследование гидродинамических характеристик электрического взрыва проводников в воде // Физические основы электрического взрыва: Сб. науч. тр. / Под ред. Гулого Г.А. – Киев: Наук. думка, 1983. – 136 с.

30. Крутиков В.С. Определение гидродинамических характеристик в конечной системе // Основные проблемы разрядно-импульсной технологии: Сб. науч. тр. – Киев: Наук. думка, 1980. – 170 с.

31. Пилипенко В.В. Кавитационные автоколебания. – Киев: Наук. думка, 1989. – 316 с.

32. Столович Н.Н. Электровзрывные преобразователи энергии. – Минск: Наука и техника, 1983. – 152 с.

33. Чачин В.Н. Электрогидравлическая обработка машиностроительных материалов. – Минск: Наука и техника, 1978. – 184 с.

Рисунки

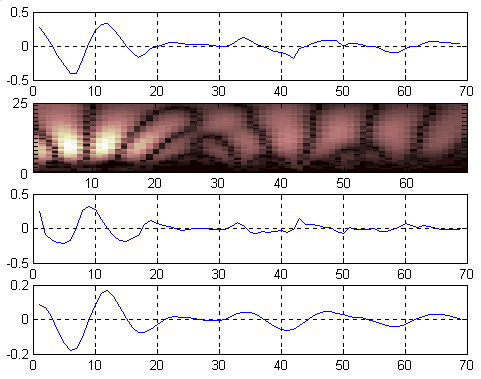
Рис. 1

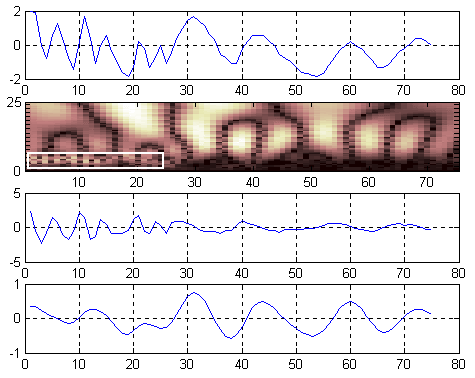
Рис. 2

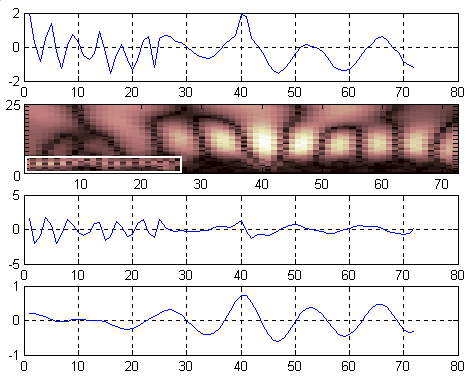
Рис.3

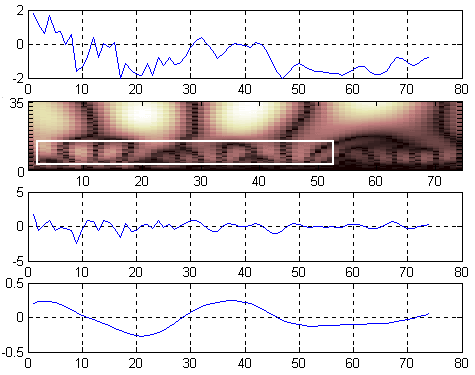
Рис. 4

 

Наверх

Список литературы

1. Алексеев К.А., Алексеева М.Б. Идентификация динамических характеристик датчиков в базисе функций Уолша // Информационно-измерительная техника: Межвуз. сб. науч. тр. - Пенза: Пенз. гос. ун-т, 2000. - Вып. 25. - С. 62-70 

2. Алексеев К.А. Задача идентификации полных и частных динамических характеристик широкополосных пьезоэлектрических датчиков переменных давлений // Приборы и системы. Управление, контроль, диагностика, 2000, №7. - C. 58-61 

3. Алексеев К.А. Способы идентификации элементов систем измерения, контроля и управления // Тез. докл. 3 Междунар. науч.-техн. конф. "Управление в технических системах - XXI век", Ковров, 2000. - С. 75 - 76 

4. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов: Пер. с англ. / Под ред. Фоменко И.Б. - М.: Связь, 1980. -248 с. 

5. Багдатьев Е.Е., Ефимова А.А. Идентификация преобразователей переменных давлений // Измерительная техника, 1986, №6. - С. 17-18 

6. Багдатьев Е.Е., Ефимова А.А., Санина Э.Б. Импульсная установка для идентификации датчиков переменных давлений // Измерительная техника, 1989, №3. - С. 18-19 

7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. - М.: Наука, 1976. - 320 с. 

8. Бендат Дж., Пирсол А. Применения корреляционного и спектрального анализа. - М.: Мир, 1983. - 312 с. 

9. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов: Пер. с англ. - М.: Мир, 1971. - 408 с.

10. Бриллинджер Д. Временные ряды. Обработка данных и теория: Пер. с англ. - М.: Мир, 1980. - 536 с. 

11. Воеводин В.В. Линейная алгебра. - М.: Наука, 1974. - 336 с. 

12. Гольденберг Л.М. и др. Цифровая обработка сигналов: Справочник / Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. - М.: Радио и связь, 1985. - 312 с. 

13. Гутников В.С. Фильтрация измерительных сигналов. - Л.: Энергоатомиздат, 1990. - 192 с. 

14. Дьяконов В.П., Абраменкова И.В. MatLab 5.0/5.3. Система символьной математики. - М.: Нолидж, 1999. - 640 с. 

15. Иосифов В.П., Алексеев К.А. Алгоритм Берга в задачах спектрального оценивания коротких откликов датчиков // Приборы и системы управления, №7, 1999. - С. 32-35 

16. Истомина Т.В., Чувыкин Б.В., Щеголев В.Е. Применение теории wavelets в задачах обработки информации. - Пенза: Изд-во Пенз. гос. ун-та, 2000. - 188 с. 

17. Кравченко В.Ф., Рвачев В.А. Wavelet-системы и их применение в обработке сигналов // Зарубежная радиоэлектроника, 1996, №4. - С. 3 - 20 

18. Кузнецов Е.А. Автоматизированный комплекс для определения статико-динамических характеристик датчиков давления в широком диапазоне температур // Измерительная техника, 1993, №6. - С. 40-43 

19. Макс Ж. Методы и техника обработки сигналов при физических измерениях. - М.: Мир, 1983. - Т.1. - 312 с. 

20. Новиков И.Я., Стечкин С.Б. Основы теории всплесков // Успехи математических наук, 1998, №6. - С. 53 - 128 

21. Новиков Л.В. Основы вейвлет-анализа сигналов. - СПб., 1999. - 152 с. 

22. Новиков Л.В. Спектральный анализ сигналов в базисе вейвлетов // Научное приборостроение, 2000, №3. - С. 57-64 

23. Осадчий Е.П., Алексеев К.А. Идентификация импульсных характеристик датчиков переменных давлений с использованием матриц двумерных нестационарных передаточных функций // Датчики и системы, 1999, №6. - С. 16 - 19 

24. Пойда В.Н. Спектральный анализ в дискретных ортогональных базисах. - Минск: Наука и техника, 1978. - 136 с. 

25. Потемкин В.Г. Введение в MatLab. - М.: Диалог МИФИ, 2000. - 247 с. 

26. Применение цифровой обработки сигналов: Пер. с англ. / Под ред. Оппенгейма Э. - М.: Мир, 1980. - 552 с. 

27. Трахтман А.М., Трахтман В.А. Основы теории дискретных сигналов на конечных интервалах. - М.: Советское радио, 1975. - 208 с. 

28. Федер Е. Фракталы. - М.: Мир, 1991. - 253 с. 

29. Чувыкин Б.В. Финитные функции. Теория и инженерные приложения. - Пенза: Изд-во Пенз. гос. ун-та, 1999. - 100 с. 

30. Alexeev C.A. Spectral estimation of short responses of sensors measuring pressure // Systems Science, 1999, vol. 25, #3, pp. 99-110 

31. Frazier, M., Jawerth, B., Weiss, G. Littlewood-Paley theory and decompositions of functional spaces. AMS, 1992 

32. Sweldens, W. Wavelets: What next? // Proc. IEEE, 1996, vol.84, p. 680