Функции Statistics Toolbox
Информация в данной статье относится к релизам программы MATLAB ранее 2016 года, и поэтому может содержать устаревшую информацию в связи с изменением функционала инструментов. С более актуальной информацией вы можете ознакомиться в разделе документации MATLAB на русском языке.
Statistics Toolbox предлагает широкий спектр инструментов для статистических вычислений. Основные возможности включают: регрессионный анализ и диагностика с выбором переменной, нелинейное моделирование, моделирование вероятностей и оценка параметров, анализ чувствительности с использованием генератора случайных чисел, управление статистическими процессами и планирование эксперимента. Пакет включает 20 различных распределений вероятностей, включая T, F и Хи-квадрат.
Автор - Мищенко Зорислав Владимирович - кандидат технических наук, доцент Владимирского государственного университета.
Список функций Statistics Toolbox
Оценка параметров закона распределения по экспериментальным данным
- betafit - Оценка параметров бета распределения
- binofit - Оценка параметров биномиального распределения
- nbinfit - Оценка параметров отрицательного биномиального распределения
- expfit - Оценка параметров экспоненциального распределения
- gamfit - Оценка параметров гамма распределения
- normfit - Оценка параметров нормального распределения
- poissfit - Оценка параметров распределения Пуассона
- raylfit - Оценка параметров распределения Релея
- unifit - Оценка параметров равномерного распределения
- weibfit - Оценка параметров распределения Вейбулла
- mle - Расчет функции максимального правдоподобия
Законы распределения случайных величин
- betacdf - Бета распределение
- binocdf - Биномиальное распределение
- cdf - Параметризованная функция распределения
- chi2cdf - Функция распределения хи-квадрат
- expcdf - Экспоненциальное распределение
- ecdf - Эмпирическая функция распределения (на основе оценки Каплана-Мейера)
- fcdf - Распределение Фишера
- gamcdf - Гамма распределение
- geocdf - Геометрическое распределение
- hygecdf - Гипергеометрическое распределение
- logncdf - Логнормальное распределение
- nbincdf - Отрицательное биномиальное распределение
- ncfcdf - Смещенное распределение Фишера
- nctcdf - Смещенное распределение Стьюдента
- ncx2cdf - Cмещенное хи-квадрат распределение
- normcdf - Нормальное распределение
- poisscdf - Распределение Пуассона
- raylcdf - Распределение Релея
- tcdf - Распределение Стьюдента
- unidcdf - Дискретное равномерное распределение
- unifcdf - Непрерывное равномерное распределение
- weibcdf - Распределение Вейбулла
Функции плотности распределения случайных величин
- betapdf - Бета распределение
- binopdf - Биномиальное распределение
- chi2pdf - Функция распределения хи-квадрат
- exppdf - Экспоненциальное распределение
- fpdf - Распределение Фишера
- gampdf - Гамма распределение
- geopdf - Геометрическое распределение
- hygepdf - Гипергеометрическое распределение
- lognpdf - Логнормальное распределение
- nbinpdf - Отрицательное биномиальное распределение
- ncfpdf - Смещенное распределение Фишера
- nctpdf - Смещенное распределение Стьюдента
- ncx2pdf - Cмещенное хи-квадрат распределение
- normpdf - Нормальное распределение
- poisspdf - Распределение Пуассона
- mvnpdf - Функция плотности вероятности многомерного нормального распределения
- raylpdf - Распределение Релея
- pdf - Параметризованная функция плотности распределения
- tpdf - Распределение Стьюдента
- unidpdf - Дискретное равномерное распределение
- unifpdf - Непрерывное равномерное распределение
- weibpdf - Распределение Вейбулла
Обратные функции распределения случайных величин
- betainv - Бета распределение
- binoinv - Биномиальное распределение
- chi2inv - Функция распределения хи-квадрат
- expinv - Экспоненциальное распределение
- finv - Распределение Фишера
- gaminv - Гамма распределение
- geoinv - Геометрическое распределение
- hygeinv - Гипергеометрическое распределение
- icdf - Параметризованная обратная функция распределения
- logninv - Логнормальное распределение
- nbininv - Отрицательное биномиальное распределение
- ncfinv - Смещенное распределение Фишера
- nctinv - Смещенное распределение Стьюдента
- ncx2inv - Cмещенное хи-квадрат распределение
- norminv - Нормальное распределение
- poissinv - Распределение Пуассона
- raylinv - Распределение Релея
- tinv - Распределение Стьюдента
- unidinv - Дискретное равномерное распределение
- unifinv - Непрерывное равномерное распределение
- weibinv - Распределение Вейбулла
Генерация псевдослучайных чисел по заданному закону распределения
- betarnd - Бета распределение
- binornd - Биномиальное распределение
- chi2rnd - Функция распределения хи-квадрат
- exprnd - Экспоненциальное распределение
- frnd - Распределение Фишера
- gamrnd - Гамма распределение
- geornd - Геометрическое распределение
- hygernd - Гипергеометрическое распределение
- iwishrnd - Обратная матрица случайных чисел распределения Уишарта
- lognrnd - Логнормальное распределение
- mvnrnd - Многомерное нормальное распределение
- mvtrnd - Многомерное распределение Стьюдента
- nbinrnd - Отрицательное биномиальное распределение
- ncfrnd - Смещенное распределение Фишера
- nctrnd - Смещенное распределение Стьюдента
- ncx2rnd - Cмещенное хи-квадрат распределение
- normrnd - Нормальное распределение
- poissrnd - Распределение Пуассона
- random - Параметризованная функция генерации псевдослучайных чисел
- raylrnd - Распределение Релея
- trnd - Распределение Стьюдента
- unidrnd - Дискретное равномерное распределение
- unifrnd - Непрерывное равномерное распределение
- weibrnd - Распределение Вейбулла
- wishrnd - Матрица случайных чисел распределения Уишарта
Оценка математического ожидания и дисперсии по заданному закону распределения и его параметрам
- betastat - Бета распределение
- binostat - Биномиальное распределение
- chi2stat - Функция распределения хи-квадрат
- expstat - Экспоненциальное распределение
- fstat - Распределение Фишера
- gamstat - Гамма распределение
- geostat - Геометрическое распределение
- hygestat - Гипергеометрическое распределение
- lognstat - Логнормальное распределение
- nbinstat - Отрицательное биномиальное распределение
- ncfstat - Смещенное распределение Фишера
- nctstat - Смещенное распределение Стьюдента
- ncx2stat - Смещенное хи-квадрат распределение
- normstat - Нормальное распределение
- poisstat - Распределение Пуассона
- raylstat - Распределение Релея
- tstat - Распределение Стьюдента
- unidstat - Дискретное равномерное распределение
- unifstat - Непрерывное равномерное распределение
- weibstat - Распределение Вейбулла
Расчет логарифма функции максимального правдоподобия
- betalike - Расчет логарифма функции максимального правдоподобия бета распределения
- gamlike - Расчет логарифма функции максимального правдоподобия гамма распределения
- normlike - Расчет логарифма функции максимального правдоподобия нормального распределения
- weiblike - Расчет логарифма функции максимального правдоподобия распределения Вейбулла
- nbinlike - Расчет логарифма функции максимального правдоподобия отрицательного биномиального распределения
Функции описательной статистики
- bootstrp - Бутстреп оценки. Оценка статистик для данных с дополненным объемом выборки посредством математического моделирования
- corrcoef - Оценка коэффициента корреляции (функция MATLAB)
- cov - Оценка матрицы ковариаций (функция MATLAB)
- crosstab - Кросстабуляция для нескольких векторов с положительными целыми элементами
- geomean - Среднее геометрическое
- grpstats - Сводные статистики по группам
- harmmean - Среднее гармоническое
- iqr - Разность между 75% и 25% квантилями или между 3-й и 1-ой квартилями
- kurtosis - Оценка коэффициента эксцесса (в отечественной литературе коэффициент эксцесса определяется как b2=kurtosis-3)
- mad - Среднее абсолютное отклонение от среднего значения
- mean - Среднее арифметическое (функция MATLAB)
- median - Медиана (функция MATLAB)
- moment - Оценка центрального момента. Порядок момента задается как аргумент функции
- nanmax - Максимальное значение в выборке. Нечисловые значения в выборке игнорируются
- nanmean - Среднее арифметическое выборки. Нечисловые значения в выборке игнорируются
- nanmedian - Медиана выборки. Нечисловые значения в выборке игнорируются
- nanmin - Минимальное значение в выборке. Нечисловые значения в выборке игнорируются
- nanstd - Оценка среднего квадратического отклонения выборки. Нечисловые значения в выборке игнорируются
- nansum - Сумма элементов выборки. Нечисловые значения в выборке игнорируются
- prctile - Выборочная процентная точка (процентиль)
- range - Размах выборки
- skewness - Оценка коэффициента асимметрии
- std - Оценка среднего квадратического отклонения (функция MATLAB)
- tabulate - Определение частот целых положительных элементов вектора случайных значений
- trimmean - Оценка среднего арифметического значения, находимая с игнорированием заданного процента минимальных и максимальных элементов в выборки
- var - Оценка дисперсии
Функции статистических графиков
- boxplot - График "Ящик с усами". График 0%, 25%, 50%, 75%, 100% процентилей выборки
- cdfplot - График кумулятивной кривой по эмпирическим данным
- fsurfht - Контурный график заданной функции. Операция построения графика выполняется интерактивно.
- gline - Операция прорисовки прямой линии в текущем графике
- gname - Нанесение меток на график
- gplotmatrix - Матрица графиков рассеяния группированных по общей переменной
- gscatter - График рассеяния двух переменных группированных по значениям третьей переменной
- lsline - График рассеяния двух переменных с линией регрессии по методу наименьших квадратов
- normplot - Нормальный вероятностный график
- qqplot - График "квантиль-квантиль" для двух выборок
- refcurve - Построение полиномиальной кривой на текущий график
- refline - Построение прямой на текущий график
- surfht - Контурный график по матрице данных
- weibplot - Вероятностный график Вейбулла
Функции статистического контроля качества
- capable - Расчет индексов воспроизводимости процесса Cp, Сpk
- capaplot - График воспроизводимости процесса
- ewmaplot - Контрольная карта экспоненциально взвешенного среднего
- histfit - Гистограмма по негруппированным экспериментальным данным с наложенной на нее кривой функции плотности распределения нормального закона
- normspec - График функции плотности нормального закона с наложенными границами допусков контролируемого параметра
- schart - Контрольная карта среднего квадратического отклонения
- xbarplot - Контрольная карта среднего арифметического
Функции линейного регрессионного анализа
- kruskalwalli - Непараметрический однофакторный дисперсионный анализ Краскала-Уоллиса
- anova1 - Однофакторный дисперсионный анализ
- anova2 - Двухфакторный дисперсионный анализ
- anovan - Многофакторный дисперсионный анализ
- aoctool - Однофакторный анализ ковариационных моделей. Выходными параметрами функции являются:
- Интерактивный график исходных данных линейных математических моделей
- Таблица однофакторного дисперсионного анализа ·
- Таблица с оценками параметров математических моделей - dummyvar - Условное кодирование переменных. Функция возвращает матрицу единиц и нулей содержащую число колонок равное сумме чисел возможных значений в столбцах исходной матрицы. Единицы и нули характеризуют отсутствие или наличие определенного значения в каждой колонки исходной матрицы.
- friedman - Тест Фридмана (непараметрический двухфакторный дисперсионный анализ Фридмана)
- glmfit - Определение параметров обобщенной линейной модели
- glmval - Прогнозирование с использованием обобщенной линейной модели
- kruskalwallis - Тест Краскала-Уоллиса (непараметрический однофакторный дисперсионный анализ)
- leverage - Оценка степени влияния отдельных наблюдений в исходном многомерном множестве данных на значения параметров линии регрессии.
- lscov - Линейная регрессия (метод наименьших квадратов) при заданной матрице ковариаций (встроенная функция MATLAB)
- manova1 - Однофакторный многомерный дисперсионный анализ
- manovacluster - Дендрограмма, показывающая группировку исходных данных в кластеры по средним значениям. В качестве исходных данных используются выходные данные однофакторного многомерного дисперсионного анализа (manova1)
- multcompare - Множественной сравнение оценок средних, параметров линии регрессии и т.д. В качестве входных параметров используются выходные параметры функций anova1, anova2, anovan, aoctool, friedman, kruskalwallis.
- polyconf - Определение доверительных интервалов для линии регрессии
- polyfit - Полиномиальная регрессия (встроенная функция MATLAB)
- polyval - Прогноз с использованием полиномиальной регрессии (встроенная функция MATLAB)
- rcoplot - График остатков
- regress - Множественная линейная регрессия
- regstats - Функция диагностирования линейной множественной модели. Графический интерфейс.
- ridge - Линейная регрессия с применением гребневых оценок (ридж-регрессия)
- rstool - Интерактивный подбор и визуализация поверхности отклика
- robustfit - Робастная оценка параметров регрессионной модели
- stepwise - Пошаговая регрессия (графический интерфейс пользователя)
Функции нелинейного регрессионного анализа
- lsqnonneg - Функция реализует метод наименьших квадратов и возвращает только неотрицательные значения параметров модели (встроенная функция MATLAB)
- nlinfit - Нелинейный метод наименьших квадратов (метод Гаусса-Ньютона)
- nnls - Решение системы линейных уравнений методом наименьших квадратов для неотрицательных значений аргумента
- nlintool - График прогнозируемых значений
- nlparci - Вектор доверительных интервалов для параметров модели
- nlpredci - Прогнозируемые значения и их доверительные интервалы
Функции планирования эксперимента
- bbdesign - Планы Бокса-Бенкена
- candexch - D-оптимальный план (на основе алгоритма перестановки строк для формирования множества возможных значений)
- candgen - Генерирует множество возможных сочетаний факторов соответствующих D-оптимальному плану
- ccdesign - Центральный композиционный план
- cordexch - Функция для определения точного D-оптимального плана эксперимента на основе алгорима обмена координатами
- daugment - Определение матрица плана дополняющую матрицу заданного плана до D-оптимального
- dcovary - Функция для построения D-оптимального блочного плана
- ff2n - Определение плана полного факторного эксперимента для факторов имеющих 2 уровня
- fracfact - Функция для формирования двухуровнего дробного факторного плана
- fullfact - Функция формирования плана полного факторного эксперимента для числа уровней факторов задаваемых пользователем
- hadamard - Матрица Адамара. Матрица Адамара соответствует плану дробного факторного эксперимента для факторов, каждый из которых задан на отрезке [-1 1]. И служит для построения линейной регрессионной модели. (Встроенная функция MATLAB)
- lhsdesign - План на основе латинских квадратов
- lhsnorm - Латинские квадраты для многомерной нормальной выборки
- rowexch - Функция для определения точного D-оптимального плана на основе алгоритма обмена строк
Функции кластерного анализа
- cluster - Деление иерархического дерева кластеров (группировка выходных данных функции linkage) на отдельные кластеры
- clusterdata - Группировка матрицы исходных данных в кластеры
- cophenet - Расчет коэффициента качества разбиения исходных данных на кластеры (этот коэффициент можно рассматривать как аналог коэффициента корреляции, чем его значение ближе к 1, тем лучше выполнено разбиение на кластеры)
- dendrogram - Дендрограмма кластеров
- inconsistent - Расчет коэффициентов несовместимости для каждой связи в иерархическом дереве кластеров и может использоваться как оценка качества разбиения на кластеры
- kmeans - Кластеризация на основе внутригрупповых средних
- linkage - Формирование иерархического дерева бинарных кластеров
- pdist - Расчет парных расстояний между объектами (векторами) в исходном множестве данных
- silhouette - График силуэта кластеров
- squareform - Преобразование вектора выходных данных функции pdist в симметричную квадратную матрицу
Функции снижения размерности задачи
- factoran - Факторный анализ
- pcacov - Функция служит для реализации метода главных компонент по заданной в качестве входного параметра матрице ковариаций
- pcares - Функция служит для определения остатка после удаления заданного количества главных компонент
- princomp - Функция служит для реализации метода главных компонент по заданной в качестве входного параметра матрице исходных значений
Функции анализа многомерных случайных величин
- barttest - Тест Бартлета
- canoncorr - Канонический корреляционный анализ
- cmdscale - Классическое многомерное шкалирование
- classify - Линейный дискриминантый анализ
- mahal - Функция определяет расстояния Махаланобиса между строками двух матриц, являющихся входными параметрами.
- manova1 - Однофакторный многомерный дисперсионный анализ
- procrustes - Ортогональное вращение, позволяющее поставить в прямое соответствие одно множество точек другому
Функции нелинейного регрессионного анализа на основе графа возможных решений
- treedisp - Отображает граф возможных решений
- treefit - Построение графа возможных решений на основе исходных данных
- treeprune - Исключение незначимых решений в графе возможных решений
- treetest - Оценка погрешности узлов графа возможных решений
- treeval - Оценка параметров регрессионной модели с использованием графа возможных решений
Статистическая проверка гипотез
- ranksum - Ранговый тест Вилкоксона для проверки однородности двух генеральных совокупностей
- signrank - Знаковый тест Вилкоксона для проверки гипотезы о равенстве медиан двух выборок
- signtest - Знаковый тест для проверки гипотезы о равенстве медиан двух выборок
- ttest - t-test для одной выборки. Проверка гипотезы о равенстве (или неравенстве) математического ожидания выборки заданному значению при условии, что величина дисперсии неизвестна. Закон распределения выборки нормальный.
- ttest2 - t-test для двух выборок. Проверка гипотезы о равенстве (или неравенстве) математических ожиданий двух выборок при условии, что величины дисперсий выборок неизвестны и равны. Закон распределения выборки нормальный.
- ztest - Z-тест. Проверка гипотезы о равенстве (или неравенстве) математического ожидания выборки заданному значению при условии, что известна величина дисперсии. Закон распределения выборки нормальный.
Проверка статистических гипотез о согласии распределения экспериментальным данным
- jbtest - Тест на соответствие выборки нормальному распределению с неопределенными параметрами нормального распределения. Этот тест является асимптотическим и не может быть использован на малых выборках. Для проверки гипотезы о соответствии выборки нормальному распределению на малых выборках необходимо использовать функцию lillietest.
- kstest - Тест Колмогорова-Смирнова на соответствие выборки заданному распределению
- kstest2 - Тест Колмогорова-Смирнова на соответствие распределений двух выборок
- lillietest - Тест на соответствие выборки нормального распределения рассчитываются исходя из значений элементов в выборке.
Проверка непараметрических гипотез
- friedman - Тест Фридмана (непараметрический двухфакторный дисперсионный анализ Фридмана)
- kruskalwallis - Тест Краскала-Уоллиса (непараметрический однофакторный дисперсионный анализ)
- ksdensity - Подгонка функции плотности вероятности по экспериментальным данным
- ranksum - Ранговый тест Вилкоксона для проверки однородности двух генеральных совокупностей
- signrank - Знаковый тест Вилкоксона для проверки гипотезы о равенстве медиан двух выборок
- signtest - Знаковый тест для проверки гипотезы о равенстве медиан двух выборок
Запись и чтение данных из файлов
- caseread - Функция для чтения данных из текстового файла. Возвращает матрицу символов из текстового файла
- casewrite - Функция для записи строковой матрицу в текстовый файл
- tblread - Функция для чтения табличных данных из текстового файла
- tblwrite - Функция для записи табличных данных из текстового файла
- tdfread - Функция для чтения табличных данных разделенных знаком табуляции в строке из текстового файла
Таблица демонстрационных примеров
- aoctool - Интерактивное средство ковариационного анализа
- disttool - Интерактивное средство для исследования функций распределения случайных величин
- glmdemo - Пример использования обобщенной линейной модели
- randtool - Интерактивное средство для генерации псевдослучайных чисел
- polytool - Интерактивное определение параметров полиномиальной модели
- rsmdemo - Интерактивное моделирование химическое реакции и нелинейный регрессионный анализ
- robustdemo - Интерактивное средство для сравнения методов МНК и робастной регрессии
Таблица вспомогательных функций
- combnk - Вычисляет количество комбинаций которыми можно выбрать k объектов из n
- grp2idx - Преобразование группирующей переменной в индексы массива
- hougen - Функция прогнозирования для модели Хогена
- tiedrank - Расчет ранга выборки с учетом ее объема
- zscore - Выполняет нормализацию матрицы по колонкам. Приводит значения по колонкам матрицы к нормальным с 0 математическим ожиданием и единичной дисперсией.
betafit - Оценка параметров бета распределения
Расчет точечных и интервальных оценок параметров бета распределения
Синтаксис
phat = betafit(x)
[phat,pci] = betafit(x,alpha)
Описание
phat = betafit(x) функция служит для расчета вектора точечных оценок phat параметров бета распределения a и b по исходной выборке значений x. Значения оценок параметров определяются методом максимального правдоподобия. Выборка x задается как вектор. Значения x должны находиться в интервале [0 1].
[phat,pci] = betafit(x,alpha) функция служит для расчета точечных phat и интервальных pci оценок параметров бета распределения a и b по исходной выборке значений x. Интервальные оценки pci параметров a и b задаются в виде матрицы размерностью 2-2. Первый столбец матрицы pci содержит нижнюю и верхнюю границы доверительного интервала параметра a, второй столбец - нижнюю и верхнюю границы доверительного интервала b. Необязательный параметр alpha определяет уровень значимости. По умолчанию alpha=0,05, что соответствует 95% доверительному интервалу.
Примеры использования функции расчета точечных и интервальных оценок параметров бета распределения
Расчет точечных оценок параметров бета распределения
>> A=4;
>> B=3;
>> x = betarnd(A,B,100,1);
>> phat = betafit(x)
phat =
4.2571 2.8700
>>a= phat(1)
a =
4.2571
>>b= phat(2)
b =
2.8700
Расчет точечных и интервальных оценок параметров бета распределения для уровня значимости 0,05.
>> A=4;
>> B=3;
>> x = betarnd(A,B,100,1);
>> [p,ci] = betafit(x)
p =
4.2571 2.8700
ci =
3.1878 2.1911
5.3264 3.5489
>>a= p(1)
a =
4.2571
>>b= p(2)
b =
2.8700
>> a_low=ci(1,1)
a_low =
3.1878
>> a_high=ci(2,1)
a_low =
5.3264
>> b_low=ci(1,2)
b_low =
2.1911
>> b_high=ci(2,2)
b_high =
3.5489
Расчет точечных и интервальных оценок параметров бета распределения для уровня значимости 0,01.
>> A=4;
>> B=3;
>> x = betarnd(A,B,100,1);
>> alfa=0.01;
>> [p,ci] = betafit(x,alfa)
p =
4.2571 2.8700
ci =
2.8518 1.9778
5.6624 3.7622
binofit - Оценка точечных и интервальных оценок параметров биномиального распределения
Синтаксис
phat = binofit(x,n)
[phat,pci] = binofit(x,n)
[phat,pci] = binofit(x,n,alpha)
Описание
phat = binofit(x,n) функция служит для расчета точечной оценки phat вероятности появления некоторого события в одном опыте при n независимых повторных испытаниях, где x число появлений событий в указанной серии испытаний. Скалярное значение x или n увеличивается до размерности второго входного аргумента. Расчет вероятности появления события производится методом максимального правдоподобия.
[phat,pci] = binofit(x,n) функция служит для расчета точечной phat и интервальной pci оценки вероятности появления некоторого события в одном опыте при биномиальном распределении. Интервальная оценка представляет собой 95% доверительный интервал.
[phat,pci] = binofit(x,n,alpha) функция возвращает точечную оценку и 100(1-alpha)% доверительный интервал вероятности появления некоторого события в одном опыте при биномиальном распределении.
Примеры использования функции расчета точечных и интервальных оценок параметра биномиального распределения
Расчет точечной оценки вероятности появления некоторого события в одном опыте
при биномиальном распределении для заданной пары значений x и p.
>> p=0.6;
>> n=100;
>> x = binornd(n,p)
x =
62
>>phat = binofit(x,n)
phat =
0.6200
Расчет точечной оценки phat для вектора числа появлений событий в серии испытаний.
>> x=[1 10 5 20 30 50];
>> n=100;
>>phat = binofit(x,n)
phat =
Columns 1 through 5
0.0100 0.1000 0.0500 0.2000 0.3000
Column 6
0.5000
Расчет точечной phat и интервальной pci оценки вероятности появления некоторого события
в одном опыте для заданной пары значений x, n и доверительной вероятности 0,95.
>> x=10;
>> n=100;
>>[phat,pci] = binofit(x,n)
phat =
0.1000
pci =
0.0490 0.1762
Расчет точечных и интервальных оценок вероятности появления некоторого события
в одном опыте для векторов значений x, n и доверительной вероятности 0,95.
>> x=[1 10 5 20 30 50];
>> n=[10 100 50 200 300 500];
>> [phat,pci] = binofit(x,n)
phat =
Columns 1 through 5
0.1000 0.1000 0.1000 0.1000 0.1000
Column 6
0.1000
pci =
Columns 1 through 5
0.0025 0.0490 0.0333 0.0622 0.0685
Columns 6 through 10
0.0751 0.4450 0.1762 0.2181 0.1502
Columns 11 through 12
0.1397 0.1297
Примечание: в векторе pci первые шесть значений являются нижними границами доверительного интервала
для соответствующей точечной оценки phat, следующие шесть - верхними границами доверительного
интервала. Расчет точечных и интервальных оценок вероятности появления некоторого события в одном
опыте для уровня значимости 0,001 и пары значений x, n.
>> x=[1 10 5 20 30 50];
>> n=[5 100 30 100 200 300];
>> alfa=0.001;
>> [phat,pci] = binofit(x,n,alfa)
phat =
Columns 1 through 5
0.2000 0.1000 0.1667 0.2000 0.1500
Column 6
0.1667
pci =
Columns 1 through 5
0.0001 0.0279 0.0224 0.0894 0.0786
Columns 6 through 10
0.1032 0.8978 0.2338 0.4713 0.3564
Columns 11 through 12
0.2483 0.2472
Уровень значимости alfa может быть задан как вектор. Размерность alfa должна быть равна
количеству элементов остальных входных аргументов. Доверительный интервал рассчитывается
для сочетания соответствующих значений векторов x, n, alfa.
>> x=[1 10 5 20 30 50];
>> n=[5 100 30 100 200 300];
>> alfa=[0.001 0.005 0.01 0.02 0.03 0.05];
>> [phat,pci] = binofit(x,n,alfa)
>> [phat,pci] = binofit(x,n,alfa)
phat =
Columns 1 through 5
0.2000 0.1000 0.1667 0.2000 0.1500
Column 6
0.1667
pci =
Columns 1 through 5
0.0001 0.0346 0.0378 0.1156 0.0993
Columns 6 through 10
0.1263 0.8978 0.2120 0.4040 0.3092
Columns 11 through 12
0.2134 0.2138
NBINFIT - Расчет точечных и интервальных оценок параметров отрицательного биномиального распределения
Синтаксис
parmhat = nbinfit(x)
[parmhat,parmci] = nbinfit(x,alpha)
[...] = nbinfit(...,options)
Описание
parmhat = nbinfit(x) функция служит для расчета вектора точечных оценок parmhat параметров отрицательного биномиального распределения по методу максимального правдоподобия для заданной выборки x. Выборка x должна быть вектором.
[parmhat,parmci] = nbinfit(x,alpha) функция служит для расчета точечных parmhat и parmci оценок параметров отрицательного биномиального распределения по исходной выборке значений x методом максимального правдоподобия. Доверительный интервал parmci рассчитывается для заданного уровня значимости alpha. Доверительная вероятность определяется как 100*(1-alpha). По умолчанию, в случае отсутствия параметра alpha, уровень значимости равен 0,05.
[...] = nbinfit(...,options) в этом варианте синтаксиса, кроме указанных в предыдущем случае параметров, задается способ оптимизации при расчете оценок параметров по методу максимального правдоподобия. Установка параметров оптимизации в nbinfit выполняется с помощью структуры options. Формирование структуры options выполняется с помощью функции optimset. В процессе работы nbinfit полученная структура данных options передается как входной аргумент функции fminsearch, выполняющей минимизацию значения отрицательного логарифма функции максимального правдоподобия отрицательного биномиального распределения. Предусмотрены следующие способы оптимизации:
|
Параметр оптимизации |
Значение параметра |
Описание |
|
Display |
'off' | 'iter' | 'final' | 'notify' |
Определяет вид выходной информации. Значение 'off' подавляет вывод результата; 'iter' отображает результаты каждой итерации; 'final' определяет вывод окончательных результатов расчета; 'notify' отображает результаты расчета в случае отсутствия сходимости. |
|
MaxFunEvals |
Положительное целое число |
Максимальное допустимое число вызовов функции |
|
MaxIter |
Положительное целое число |
Максимальное допустимое число итераций |
|
TolFun |
Положительное вещественное число |
Предельное значение точности при вычислении функции |
|
TolX |
Положительное вещественное число |
Предельное значение точности при использовании аргумента |
Приведенные в таблице параметры являются общими для функций оптимизации ядра Matlab и Optimization Toolbox. Функции оптимизации Optimization Toolbox содержат ряд дополнительных настроек. Информацию о них можно получить в справочной системе в разделе описания функции optimset.По умолчанию предусмотрена установка параметра 'Display' со значением 'notify', т.е. optimset('Display','notify').
Примечание: дисперсия отрицательного биномиального распределения должна быть больше математического ожидания. Поэтому, если точечная оценка дисперсии больше среднего арифметического по выборке x, nbinfit нельзя использовать при расчете точечных и интервальных оценок параметров отрицательного биномиального распределения. В этом случае вместо nbinfit используется nbinfit.
Примеры использования функции расчета точечных и интервальных оценок параметров отрицательного биномиального распределения
Расчет точечных оценок параметров отрицательного биномиального распределения
>> R=10;
>> P=0.5;
>> x = nbinrnd(R,P,100,1);
>> parmhat = nbinfit(x)
parmhat =
7.3336 0.4180
>>r= parmhat(1)
r =
7.3336
>>p= parmhat(2)
p =
0.4180
Расчет точечных и интервальных оценок параметров отрицательного биномиального распределения
для уровня значимости 0,05.
>> R=10;
>> P=0.5;
>> x = nbinrnd(R,P,100,1);
>> [parmhat,parmci] = nbinfit(x)
parmhat =
7.3336 0.4180
parmci =
3.5922 0.2880
11.0749 0.5481
Расчет точечных и интервальных оценок параметров отрицательного биномиального распределения
для уровня значимости 0,01.
>> R=10;
>> P=0.5;
>> alfa=0.01;
>> x = nbinrnd(R,P,100,1);
>> [parmhat,parmci] = nbinfit(x, alfa)
parmhat =
7.3336 0.4180
parmci =
2.4166 0.2471
12.2505 0.5890
Расчет точечных и интервальных оценок параметров отрицательного биномиального распределения
для уровня значимости 0,01. При расчете установлены следующие параметры оптимизации:
1. вывод результатов каждой итерации, 2. максимальное количество итераций не более 20.
>> R=10;
>> P=0.5;
>> alfa=0.01;
>> x = nbinrnd(R,P,100,1);
>> options = optimset('Display','iter','MaxIter',20);
>> [parmhat,parmci] = nbinfit(x, alfa, options)
Iteration Func-count min f(x) Procedure
1 2 -1349.86 initial
2 4 -1349.86 contract inside
3 6 -1349.86 contract inside
4 8 -1349.86 contract inside
5 10 -1349.86 contract inside
6 12 -1349.86 contract inside
7 14 -1349.86 contract inside
8 16 -1349.86 contract inside
9 18 -1349.86 contract inside
10 20 -1349.86 contract inside
11 22 -1349.86 contract inside
12 24 -1349.86 contract inside
13 26 -1349.86 contract inside
14 28 -1349.86 contract inside
Optimization terminated successfully:
the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-004
and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 1.000000e-004
parmhat =
8.4533 0.4551
parmci =
2.8032 0.2856
14.1033 0.6247
EXPFIT - Расчет точечных и интервальных оценок параметров экспоненциального распределения
Синтаксис
muhat = expfit(x)
[muhat,muci] = expfit(x)
[muhat,muci] = expfit(x,alpha)
Описание
muhat = expfit(x) функция служит для расчета точечной оценки muhat параметра ![]() экспоненциального распределения по исходной выборке значений x. Значения оценок параметров определяются методом максимального правдоподобия.
экспоненциального распределения по исходной выборке значений x. Значения оценок параметров определяются методом максимального правдоподобия.
[muhat,muci] = expfit(x) позволяет рассчитать точечную muhat и интервальную muci оценок параметра ![]() экспоненциального распределения по исходной выборке значений x для доверительной вероятности равной 95%.
экспоненциального распределения по исходной выборке значений x для доверительной вероятности равной 95%.
[muhat,muci] = expfit(x,alpha) служит для расчета точечной muhat и интервальной muci оценок параметра ![]() экспоненциального распределения по исходной выборке значений x для заданного уровня значимости alfa. Доверительная вероятность определяется как (1-alfa).
экспоненциального распределения по исходной выборке значений x для заданного уровня значимости alfa. Доверительная вероятность определяется как (1-alfa).
Выборка x может быть задана как вектор или матрица. Во втором случае, точечная оценка muhat и интервальная оценка muci рассчитывается для каждого столбца матрицы x.
Значение уровня значимости alfa может быть задано как скаляр для всех выборок в матрице х, или отдельно для каждого столбца х. Во втором случае размерность вектора alfa должна быть равна числу столбцов в матрице х.
Примеры использования функции расчета точечных и интервальных оценок параметров экспоненциального распределения
Расчет точечной оценки параметра ![]() для вектора выборки x.
для вектора выборки x.
>> mu=2
mu =
2
>> x=exprnd(mu,100,1);
>> muhat = expfit(x)
muhat =
1.4444
Расчет точечных оценок параметра ![]() для столбцов матрицы выборки х.
для столбцов матрицы выборки х.
>> mu=2;
>> x=exprnd(mu,100,2);
>> muhat = expfit(x)
muhat =
1.9423 2.4986
Расчет точечной и интервальной оценки параметра ![]() для вектора выборки наблюдений x.
для вектора выборки наблюдений x.
Доверительный интервал соответствует 95% вероятности.
>> mu=2
mu =
2
>> x=exprnd(mu,100,1);
>> [muhat,muci] = expfit(x)
muhat =
2.0643
muci =
1.6796
2.4880
Расчет точечных и интервальных оценок параметра ![]() для столбцов матрицы выборки х.
для столбцов матрицы выборки х.
Доверительный интервал соответствует 95% вероятности.
>> mu=2;
>> x=exprnd(mu,100,2);
>> [muhat,muci] = expfit(x)
muhat =
2.2296 1.8457
muci =
1.8141 1.5017
2.6874 2.2246
Расчет точечных и интервальных оценок параметра ![]() для столбцов матрицы выборки х и уровне значимости 0,01.
для столбцов матрицы выборки х и уровне значимости 0,01.
>> mu=2;
>> alfa=0.01;
>> x=exprnd(mu,100,2);
>> [muhat,muci] = expfit(x,alfa)
muhat =
2.2047 1.8899
muci =
1.6782 1.4386
2.8139 2.4121
Доверительная вероятность может быть задана отдельно для каждой выборки в матрице x.
>> mu=2;
>> alfa=[0.05 0.001];
>> x=exprnd(mu,10000,2);
>> [muhat,muci] = expfit(x,alfa)
muhat =
2.3413 2.0181
muci =
1.9049 1.4193
2.8219 2.7488
GAMFIT - Расчет точечных и интервальных оценок параметров Гамма распределения
Синтаксис
phat = gamfit(x)
[phat,pci] = gamfit(x)
[phat,pci] = gamfit(x,alpha)
Описание
phat = gamfit(x) функция служит для расчета вектора точечных оценок phat параметров Гамма распределения a и b по исходной выборке значений x. Значения оценок параметров определяются методом максимального правдоподобия. Выборка x задается как вектор.
[phat,pci] = gamfit(x) функция служит для расчета точечных phat и интервальных pci оценок параметров Гамма распределения a и b по исходной выборке значений x. Интервальные оценки pci параметров a и b задаются в виде матрицы размерностью 2-2. Первый столбец матрицы pci содержит нижнюю и верхнюю границы доверительного интервала параметра a, второй столбец - нижнюю и верхнюю границы доверительного интервала b. Интервальная оценка параметров Гамма распределения соответствует 95% доверительной вероятности.
[phat,pci] = gamfit(x,alpha) в отличие от второго варианта синтаксиса в качестве второго входного параметра задается уровень значимости alpha. Доверительная вероятность для интервальной оценки параметров a, b определяется как (1- alpha).
Примеры использования функции расчета точечных и интервальных оценок параметров Гамма распределения
Расчет точечных оценок параметров Гамма распределения
>> A=4;
>> B=3;
>> x = gamrnd(A,B,100,1);
>> phat = gamfit(x)
phat =
3.4797 3.3897
>>a= phat(1)
a =
3.4797
>>b= phat(2)
b =
3.3897
Расчет точечных и интервальных оценок параметров Гамма распределения для уровня значимости 0,05.
>> A=5;
>> B=2;
>> x = gamrnd(A,B,100,1);
>> [phat,pci] = gamfit(x)
phat =
5.0306 1.9073
pci =
3.4819 1.3436
6.5792 2.4711
>>a= phat (1)
a =
5.0306
>> b= phat (2)
b =
1.9073
>> a_low= pci (1,1)
a_low =
3.4819
>> a_high= pci (2,1)
a_high =
6.5792
>> b_low= pci (1,2)
b_low =
1.3436
>> b_high= pci (2,2)
b_high =
2.4711
Расчет точечных и интервальных оценок параметров Гамма распределения для уровня значимости 0,01.
>> A=5;
>> B=2;
>> alfa=0.01;
>> x = gamrnd(A,B,100,1);
>> [phat,pci] = gamfit(x, alfa)
phat =
5.9167 1.8883
pci =
3.6012 1.0733
8.2322 2.7034
NORNFIT - Расчет точечных и интервальных оценок параметров нормального закона
Синтаксис
[muhat,sigmahat,muci,sigmaci] = normfit(X)
[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha)
Описание
[muhat,sigmahat,muci,sigmaci] = normfit(X) позволяет рассчитать точечные и интервальные оценки параметров нормального закона: для математического ожидания - muhat, muci; для среднего квадратического отклонения - sigmahat, sigmaci. Исходная выборка Х может быть задана в виде вектора или матрицы. Если Х является вектором, то первый элемент векторов интервальных оценок muci и sigmaci соответствует нижней границе доверительного интервала, второй - верхней границе. Если X является матрицей, то каждый столбец рассматривается как отдельная выборка. Точечные оценки muhat и sigmahat являются векторами с числом элементов равным количеству столбцов в матрице Х. Интервальные оценки muci и sigmaci представляются как матрицы с размерностью 2xn, где n - число столбцов в матрице Х. Первая строка матриц muci и sigmaci является нижней границей доверительного интервала, вторая - верхней. Доверительный интервал параметров нормального закона соответствует уровню значимости равному 0,05.
[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha) в отличии от первого варианта синтаксиса, необязательный параметр alpha задает уровень значимости для доверительных интервалов математического ожидания и среднего квадратического отклонения. Доверительная вероятность интервальных оценок параметров нормального закона определяется как 100(1-alpha)%.
Примеры использования функции расчета точечных и интервальных оценок параметров нормального закона
Расчет точечных оценок параметров нормального закона
>> MU=0;
>> SIGMA=1;
>> X=normrnd(MU,SIGMA,100,1);
>> [muhat,sigmahat] = normfit(X)
muhat =
0.0479
sigmahat =
0.8685
Расчет точечных и интервальных оценок параметров нормального закона для уровня значимости 0,05.
>> MU=0;
>> SIGMA=1;
>> X=normrnd(MU,SIGMA,100,1);
>> [muhat,sigmahat,muci,sigmaci] = normfit(X)
muhat =
0.0479
sigmahat =
0.8685
muci =
-0.1244
0.2203
sigmaci =
0.7626
1.0089
Расчет точечных и интервальных оценок параметров нормального закона для уровня значимости 0,01.
>> MU=0;
>> SIGMA=1;
>> alfa=0.01;
>> X=normrnd(MU,SIGMA,100,1);
>> [muhat,sigmahat,muci,sigmaci] = normfit(X,alfa)
muhat =
0.0479
sigmahat =
0.8685
muci =
-0.1802
0.2760
sigmaci =
0.7330
1.0596
Расчет точечных и интервальных оценок параметров нормального закона для двух выборок,
заданных в виде матрицы Х с размерностью 100x2. Уровень значимости доверительных интервалов
параметров нормального закона для обеих выборок равен 0,05.
>> MU=0;
>> SIGMA=1;
>> X=normrnd(MU,SIGMA,100,2);
>> [muhat,sigmahat,muci,sigmaci] = normfit(X,alfa)
muhat =
-0.0099 -0.1476
sigmahat =
0.9977 0.9659
muci =
-0.2719 -0.4013
0.2522 0.1061
sigmaci =
0.8421 0.8152
1.2173 1.1784
Расчет точечных и интервальных оценок параметров нормального закона для двух выборок,
заданных в виде матрицы Х с размерностью 100x2. Уровень значимости доверительных интервалов
параметров нормального закона для выборок равен соответственно 0,05 и 0,001.
>> MU=0;
>> SIGMA=1;
>> alfa=[0.05 0.001];
>> X=normrnd(MU,SIGMA,100,2);
>> [muhat,sigmahat,muci,sigmaci] = normfit(X,alfa)
muhat =
-0.0677 0.0572
sigmahat =
0.9777 0.8690
muci =
-0.2617 -0.1153
-0.3993 -0.2375
sigmaci =
1.2652 1.1244
1.1358 1.0095
POISSFIT - Расчет точечных и интервальных оценок параметров закона Пуассона
Синтаксис
lambdahat = poissfit(X)
[lambdahat,lambdaci] = poissfit(X)
[lambdahat,lambdaci] = poissfit(X,alpha)
Описание
lambdahat = poissfit(X) функция служит для расчета точечной оценки lambdahat параметра ![]() распределения Пуассона по исходной выборке значений Х. Значения оценок параметров определяются методом максимального правдоподобия.
распределения Пуассона по исходной выборке значений Х. Значения оценок параметров определяются методом максимального правдоподобия.
[lambdahat,lambdaci] = poissfit(X) позволяет рассчитать точечную lambdahat и интервальную lambdaci оценки параметра ![]() распределения Пуассона по исходной выборке значений Х для доверительной вероятности равной 95%.
распределения Пуассона по исходной выборке значений Х для доверительной вероятности равной 95%.
[lambdahat,lambdaci] = poissfit(X,alpha) служит для расчета точечной lambdahat и интервальной lambdaci оценок параметра ![]() распределения Пуассона по исходной выборке значений X для заданного уровня значимости alfa. Доверительная вероятность определяется как 100(1-alpha)%.
распределения Пуассона по исходной выборке значений X для заданного уровня значимости alfa. Доверительная вероятность определяется как 100(1-alpha)%.
Точечная оценка параметра ![]() по методу максимального правдоподобия определяется как среднее арифметическое значений Xi:
по методу максимального правдоподобия определяется как среднее арифметическое значений Xi:
![]()
Выборка Х может быть задана как вектор или матрица. Во втором случае, точечная оценка lambdahat и интервальная оценка lambdaci рассчитывается для каждого столбца матрицы Х.
Значение уровня значимости alfa может быть задано как скаляр для всех выборок в матрице Х, или отдельно для каждого столбца Х. Во втором случае размерность вектора alfa должна быть равна числу столбцов в матрице Х lambdaci.
Примеры использования функции расчета точечных и интервальных оценок параметров распределения Пуассона
>> LAMBDA=1
LAMBDA =
1
>> X=poissrnd(LAMBDA,100,1);
>> lambdahat = poissfit(X)
lambdahat =
0.9500
Расчет точечных оценок параметра ![]() для столбцов матрицы выборки Х.
для столбцов матрицы выборки Х.
>> LAMBDA=1
LAMBDA =
1
>> X=poissrnd(LAMBDA,100,2);
>> lambdahat = poissfit(X)
lambdahat =
1.2100 1.0100
Расчет точечной и интервальной оценки параметра ![]() для вектора выборки наблюдений Х.
для вектора выборки наблюдений Х.
Доверительный интервал соответствует 95% вероятности.
>> LAMBDA=1;
>> X=poissrnd(LAMBDA,100,1);
>> [lambdahat,lambdaci] = poissfit(X)
lambdahat =
1.0900
lambdaci =
0.8854
1.2946
Расчет точечных и интервальных оценок параметра ![]() для столбцов матрицы выборки X.
для столбцов матрицы выборки X.
Доверительный интервал соответствует 95% вероятности.
>> LAMBDA=1;
>> X=poissrnd(LAMBDA,100,2);
>> [lambdahat,lambdaci] = poissfit(X)
lambdahat =
0.8600 0.9600
lambdaci =
0.6879 0.7776
1.0621 1.1723
Расчет точечных и интервальных оценок параметра ![]() для столбцов матрицы выборки X и уровне значимости 0,01.
для столбцов матрицы выборки X и уровне значимости 0,01.
>> LAMBDA=1;
>> alpha=0.01;
>> X=poissrnd(LAMBDA,100,2);
>> [lambdahat,lambdaci] = poissfit(X, alpha)
lambdahat =
1.0600 0.9800
lambdaci =
0.7948 0.7438
1.3252 1.2650
Доверительная вероятность может быть задана отдельно для каждой выборки в матрице X.
>> LAMBDA=1;
>> alpha=[0.05 0.05];
>> X=poissrnd(LAMBDA,100,2);
>> [lambdahat,lambdaci] = poissfit(X, alpha)
lambdahat =
0.9500 0.9800
lambdaci =
0.7686 0.7956
1.1613 1.1943
RAYLFIT - Расчет точечных и интервальных оценок параметров закона Релея
Синтаксис
phat = raylfit(data)
[phat, pci] = raylfit(data)
[phat, pci] = raylfit(data,alpha)
Описание
phat = raylfit(data) функция служит для расчета точечной оценки phat параметра распределения Релея по исходной выборке значений data. Значения оценок параметров определяются методом максимального правдоподобия.
[phat, pci] = raylfit(data) позволяет рассчитать точечную phat и интервальную pci оценки параметра распределения Релея по исходной выборке значений data для доверительной вероятности равной 95%.
[phat, pci] = raylfit(data,alpha) служит для расчета точечной phat и интервальной pci оценок параметра распределения Релея по исходной выборке значений data для заданного уровня значимости alfa. Доверительная вероятность определяется как 100(1-alpha)%.
Примеры использования функции расчета точечных и интервальных оценок параметров распределения Релея
Расчет точечной оценки параметра B для вектора выборки data.
>> B=1
B =
1
>> data=raylrnd(B,100,1);
>> phat = poissfit(data)
phat =
1.2113
Расчет точечных оценок параметра B для столбцов матрицы выборки data.
>> B=1;
>> data=raylrnd(B,100,3);
>> phat = poissfit(data)
phat =
1.2342 1.3225 1.3409
Расчет точечной и интервальной оценки параметра B для вектора выборки наблюдений data.
Доверительный интервал соответствует 95% вероятности.
>> B=1;
>> data=raylrnd(B,100,1);
>> [phat, pci] = poissfit(data)
phat =
1.3938
pci =
1.1624
1.6252
Расчет точечных и интервальных оценок параметра B для столбцов матрицы выборки data.
Доверительный интервал соответствует 95% вероятности.
>> B=1;
>> data=raylrnd(B,100,3);
>> [phat, pci] = poissfit(data)
phat =
1.2884 1.1835 1.1054
pci =
1.0659 0.9703 0.8994
1.5109 1.3967 1.3115
Расчет точечных и интервальных оценок параметра B для столбцов матрицы выборки data и уровне значимости 0,01.
>> B=1;
>> alpha=0.01;
>> data=raylrnd(B,100,3);
>> [phat, pci] = poissfit(data, alpha)
phat =
1.3030 1.2477 1.3001
pci =
1.0090 0.9600 1.0064
1.5971 1.5355 1.5938
Доверительная вероятность может быть задана отдельно для каждого столбца в матрице data.
>> B=1;
>> alpha=[0.01 0.05 0.001];
>> data=raylrnd(B,100,3);
>> [phat, pci] = poissfit(data, alpha)
phat =
1.3030 1.2477 1.3001
pci =
1.0090 1.0288 0.9249
1.5971 1.4667 1.6753
mle - Расчет точечных и интервальных оценок параметров распределения заданного распределения
Синтаксис
phat = mle('dist',data)
[phat,pci] = mle('dist',data)
[phat,pci] = mle('dist',data,alpha)
[phat,pci] = mle('dist',data,alpha,p1)
Описание
phat = mle('dist',data) возвращает значения точечных оценок параметров закона распределения. Вид распределения задается строковой переменной 'dist' в соответствии со следующей таблицей. Выборка наблюдений определяется векторной переменной data.
|
Вид распределения |
Переменная 'dist' |
|
Бета |
'beta', 'Beta' |
|
Бернулли |
'Bernoulli', 'bernoulli' |
|
Биномиальное |
'bino', 'binomial' |
|
Экспоненциальное |
'exp', 'Exponential' |
|
Гамма |
'gam', 'Gamma' |
|
Геометрическое |
'geo', 'Geometric' |
|
Нормальное |
'norm', 'Normal' |
|
Пуассона |
'poiss', 'Poisson' |
|
Релея |
'rayl', 'Rayleigh', 'rayleigh' |
|
Дискретное равномерное |
'unid', 'Discrete Uniform' |
|
Непрерывное равномерное |
'unif', 'Uniform' |
|
Вейбулла |
'weib', 'Weibull' |
[phat,pci] = mle('dist',data) служит для расчета точечных phat и интервальных pci оценок параметров закона распределения, заданного переменной 'dist', по исходной выборке data. Доверительный интервал рассчитывается для 0,05 уровня значимости.
[phat,pci] = mle('dist',data,alpha) служит для расчета точечных phat и интервальных pci оценок параметров закона распределения, заданного переменной 'dist', по исходной выборке data и уровня значимости alpha. Доверительная вероятность рассчитывается по формуле 100(1-alpha)%.
[phat,pci] = mle('dist',data,alpha,p1) функция предназначена для расчета точечной phat и интервальной pci оценок вероятности появления события в одном опыте для биномиального распределения, где p1 - количество повторных независимых испытаний. В этом случае переменная 'dist' всегда равна 'bino' или 'binomial'. Входные параметры data и alpha выполняют те же функции, что и в предыдущем варианте синтаксиса.
Расчет точечных и интервальных оценок параметров закона распределения выполняется по методу максимального правдоподобия.
Функция mle является аналогом параметрических функций: генерации псевдослучайных чисел - random, расчета квантилей распределений - icdf и т.д.
Примеры использования функции mle
Расчет точечных оценок параметров нормального распределения
>> MU=0;
>> SIGMA=1;
>> data=normrnd(MU, SIGMA,100,1);
>> phat = mle('Normal',data)
phat =
0.0479 0.8641
>> mu= phat(1)
mu =
0.0479
>> sigma = phat(2)
sigma =
0.8641
Расчет точечных и интервальных оценок параметров нормального распределения при уровне значимости равном 0,01
>> MU=0;
>> SIGMA=1;
>> alfa=0.01;
>> data=normrnd(MU, SIGMA,100,1);
>>[phat,pci] = mle('Normal',data, alfa)
phat =
-0.1270 0.9400
pci =
-0.3776 0.7338
0.1236 1.1461
Расчет точечной и интервальной оценок вероятности появления события в одном опыте для биномиального распределения
при уровне значимости равном 0,01.
>> data=10;
>> p1=100;
>> alfa=0.01;
>> [phat,pci] = mle('binomial',data,alfa,p1)
phat =
0.1000
pci =
0.0382
0.2020
betacdf - Функция распределения вероятностей бета распределения
Синтаксис:
F = betacdf(x,a,b)
Описание:
betacdf(x,a,b) предназначена для расчета значений функции распределения вероятностей бета распределения для параметров распределения a, b и значения случайной величины x. Размерность векторов или матриц x, a и b должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Параметры a и b должны быть положительными. Значение случайной величины x должно находиться в интервале [0 1].
Функция распределения вероятностей бета распределения имеет вид
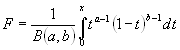 ,
,
где ![]() - Бета функция.
- Бета функция.
Выходной параметр F представляет собой значение вероятности попадания случайной величины t в интервал [0 x].
Примеры:
Использование скалярных аргументов x=0.5; a=1; b=2.
>> x=0.5
x =
0.5000
>> a=1
a =
1
>> b=2
b =
2
>> F = betaсdf(x,a,b)
F =
0.7500
Использование векторного аргумента x=[0 0,3 0,6 0, 9]; и скалярных параметров a=1; b=2.
>> x=0:0.3:1
x =
0 0.3000 0.6000 0.9000
>> a=1
a =
1
>> b=2
b =
2
>> F = betapdf(x,a,b)
F =
0 0.5100 0.8400 0.9900
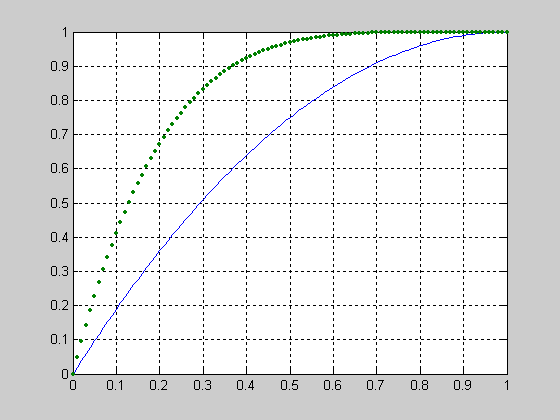
График функции распределения вероятностей с параметрами a=1; b=2 и a=1; b=5.
>> a=1; b=2;
>> x=0:0.01:1;
> F1 = betacdf(x,a,b);
>> b=5;
>> F2 = betacdf(x,a,b);
>> plot(x,F1,x,F2,'.')
>> grid on
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Вероятность попадания определяется по формуле ![]() .
.
Определение пределов интегрирования.
>> xmin=0.1;
>> xmax=0.2;
Параметры бета распределения.
>> a=1;
>> b=4;
Расчет вероятности P попадания x в интервал [xmin xmax].
>> betacdf(xmax,a,b) - betacdf(xmin,a,b)
ans =
0.2465
binocdf - Функция распределения вероятностей биномиального закона
Синтаксис:
F = binocdf(x,n,p)
Описание:
binocdf(x,n,p) служит для расчета значения функции распределения вероятностей биномиального закона для значений случайной величины x и параметров n, p. Размерность векторов или матриц x, n и p должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов.
Значение параметра n должно быть положительным целым. Значение параметра p должно находиться в интервале [0 1]. Значение случайной величины x должно быть целым, положительным и ![]() .
.
Функция распределения вероятностей биномиального закона имеет вид
![]() ,
,
где ![]() - число сочетаний, которым можно выбрать i объектов из n,
- число сочетаний, которым можно выбрать i объектов из n, ![]() ,
,
![]() - вероятность появления события в отдельном опыте,
- вероятность появления события в отдельном опыте,
![]() - вероятность отсутствия события в отдельном опыте.
- вероятность отсутствия события в отдельном опыте.
Выходной параметр F представляет собой вероятность появления некоторого события от нуля до x раз при n независимых испытаниях.
Примеры:
Использование скалярных аргументов x=5; n=10; p=0.7.
>> x=5
x =
5
>> n=10
n =
10
>> p=0.7
p =
0.7000
>> F = binopdf(x,n,p)
F =
0.1029
Использование векторного аргумента x=[1 2 3 4 5]; и скалярных параметров n=10; p=0.7.
>> x=1:5
x =
1 2 3 4 5
>> n=10
n =
10
>> p=0.7
p =
0.7000
>> F = binocdf(x,n,p)
F =
0.0001 0.0016 0.0106 0.0473 0.1503
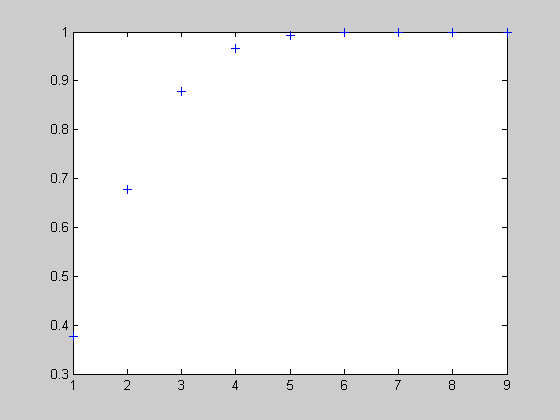
Вид функции распределения вероятностей с параметрами n=10; p=0.2.
>> n=10; p=0.2;
>> x=1:1:9;
>> F = binocdf(x,n,p);
>> plot(x,F,'+')
Определить вероятность выигрыша более чем в 100 матчах из 162 играх, если вероятность выиграть игру 50%.
Вероятность выиграть 100 и менее игр из 162 составляет:
>> P=binocdf(100,162,0.5)
P =
0.9990
Вероятность выиграть более чем в 100 матчах определяется как обратное событие к предыдущему
>> 1-P
ans =
0.0010
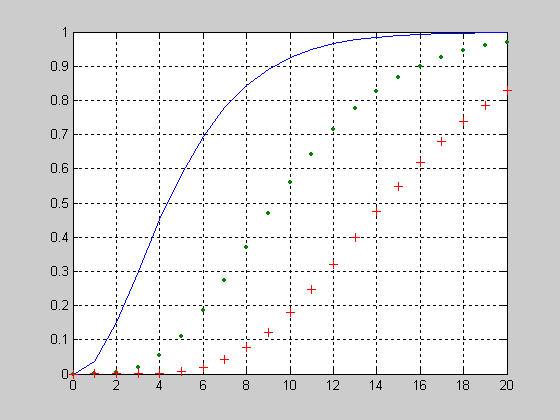
chi2cdf - Функция распределения вероятностей хи-квадрат
Синтаксис:
F = chi2cdf(x,v)
Описание:
chi2cdf(x,v) вычисляет значение функции распределения вероятностей ![]() для параметра распределения v и значения случайной величины x. Размерность матриц x и v должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Число степеней свободы v должно быть целым положительным числом.
для параметра распределения v и значения случайной величины x. Размерность матриц x и v должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Число степеней свободы v должно быть целым положительным числом.
Функция распределения вероятностей ![]() имеет вид
имеет вид
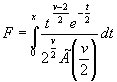 ,
,
где ![]() - Гамма-функция,
- Гамма-функция, ![]() - число степеней свободы.
- число степеней свободы.
Результат расчета F – вероятность попадания случайной величины t в интервал [0 x].
Примеры:
Использование скалярных аргументов x=0.1; v=10.
>> v=10
v =
10
>> x=0.1
x =
0.1000
>> F = chi2cdf(x,v)
F =
2.4980e-009
Использование векторного аргумента x=[0 0,3 0,6 0, 9]; и скалярного параметра v=10.
>> x=[0 0.3 0.6 0.9]
x =
0 0.3000 0.6000 0.9000
>> v=10
v =
10
>> F = chi2cdf(x,v)
F =
1.0e-003 *
0 0.0006 0.0158 0.1059
>> [x' F']
ans =
0 0
0.3000 0.0000
0.6000 0.0000
0.9000 0.0001
График функции распределения вероятностей хи-квадрат с параметрами v=[5 10 15].
>> x=0:1:20;
>> v=5;
>> F1 = chi2cdf(x,v);
>> v=10;
>> F2 = chi2cdf(x,v);
>> v=15;
>> F3 = chi2cdf(x,v);
>> plot(x,F1,x,F2,'.',x,F3,'+')
>> grid on
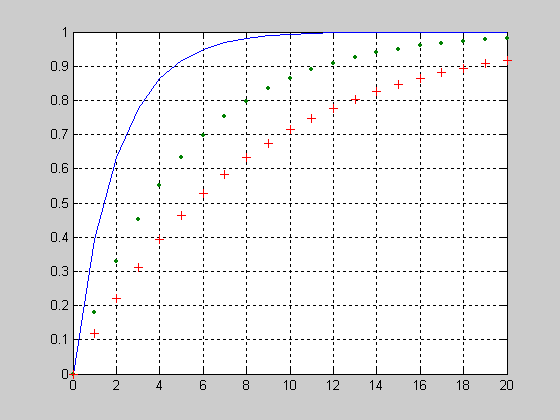
expcdf- Функция распределения вероятностей экспоненциального закона
Синтаксис:
F = expcdf(X,MU)
Описание:
expcdf(X,MU) cлужит для расчета значения функции распределения вероятностей экспоненциального закона для параметра распределения ![]() (MU) и значения случайной величины X. Размерность векторов или матриц X и MU должна быть одинаковой. Размерность скалярного параметра увеличивается до размера другого входного аргумента. Параметр
(MU) и значения случайной величины X. Размерность векторов или матриц X и MU должна быть одинаковой. Размерность скалярного параметра увеличивается до размера другого входного аргумента. Параметр ![]() должен быть положительным числом.
должен быть положительным числом.
Функция распределения вероятностей экспоненциального закона имеет вид
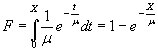 .
.
Результат расчета представляет собой значение вероятности F попадания случайной величины в интервал [0 X].
Примеры:
Использование скалярных аргументов x=0.5; a=1; b=2.
>> X=0.5
X =
0.5000
>> MU=1
MU =
1
>> F = expcdf(X,MU)
F =
0.3935
Использование векторного аргумента X=[0 0.3 0.6 0.9] и скалярного параметра MU=5.
>> X=[0 0.3 0.6 0.9]
X =
0 0.3000 0.6000 0.9000
>> MU=5
MU =
5
>> F = expcdf(X,MU)
F =
0 0.0582 0.1131 0.1647
График функции распределения вероятностей экспоненциального закона для параметра MU=[2 5 8].
>> X=0:1:20;
>> MU=2;
>> F1 = expcdf(X,MU);
>> MU=5;
>> F2 = expcdf(X,MU);
>> MU=8;
>> F3 = expcdf(X,MU);
>> plot(X,F1,X,F2,'.',X,F3,'+')
>> grid on
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Вероятность попадания определяется по формуле ![]() .
.
Определение пределов интервала.
>> xmin=0.1;
>> xmax=0.2;
Параметры распределения.
>> MU=1;
Расчет вероятности P попадания Х в интервал [xmin xmax].
>> expcdf(xmax,MU)-expcdf(xmin,MU)
ans =
0.0861
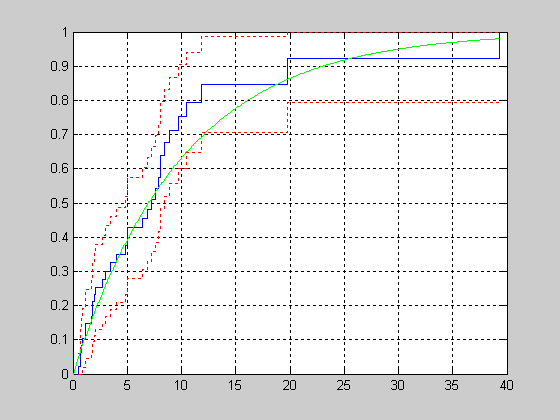
ecdf- Эмпирическая функция распределения на основе оценки Каплана-Мейера
Синтаксис:
[f,x] = ecdf(y)
[f,x,flo,fup] = ecdf(y)
[...] = ecdf(y,'param1',value1,'param2',value2,...)
Описание:
[f,x] = ecdf(y) - расчет значений эмпирической функции распределения на основе оценки Каплана-Мейера, где y – вектор исходных данных, f – вектор значений эмпирической функции распределения рассчитанной для упорядоченного ряда исходных данных х.
[[f,x,flo,fup] = ecdf(y) - кроме значений f и х позволяет определить нижнюю flo и верхнюю fup границы доверительных интервалов для значений эмпирической функции распределения. Расчет значений границ доверительных интервалов проводится по формуле Гринвуда.
[...] = ecdf(y,'param1',value1,'param2',value2,...) - дополнительные параметры 'param1', value1, 'param2', value2, ... задаются в виде строки и соответствующего ей вектора значений. Дополнительные параметры позволяют задать вид цензурированности наблюдений, частоту значений, уровень значимости и тип выходного результата. Возможные значения строковой переменной 'param' и функции вектора value приведены в следующей таблице:
|
Значение 'param' |
Функции value |
|
'censoring' |
Вектор булевых значений с размерностью х. Если элемент вектора value равен 1, то результат наблюдения считается цензурированным справа, для value=0 - нецензурированным элементом. По умолчанию все наблюдения являются нецензурированными. |
|
'frequency' |
Вектор с размерностью х содержащий положительные целые значения. J-й элемент вектора показывает частоту появления j-го элемента вектора х. По умолчанию частота значений вектора х равна 1. |
|
'alpha' |
Значение уровня значимости, служащей для расчета доверительной вероятности по формуле 100*(1-alpha)%. Величина alpha должна находиться в интервале [0 1]. По умолчанию alpha=0,05. |
|
'function' |
Тип выходного результата f. Возможные значения: 'cdf' – кумулятивная функция (по умолчанию), 'survivor' – функция выживаемости, 'cumulative hazard' – кумулятивная случайная функция. |
Примеры:
Пример построения теоретической и эмпирической функции распределения с границами доверительных интервалов для выборки из 50 элементов, распределенных по экспоненциальному закону.
Генерация двух выборок y, d на 50 элементов распределенных по экспоненциальному закону с параметрами распределения равными 10 и 20 соответственно.
>> y = exprnd(10,50,1);
>> d = exprnd(20,50,1);
Исследуемая выборка t определяется как вектор минимальных значений при поэлементном сравнении элементов векторов y и d.
>> t = min(y,d);
Определение условий цензурирования значений исследуемой выборки t.
>> censored = (y>d);
Расчет значений эмпирической функции распределения и границ доверительных интервалов.
>> [f,x,flo,fup] = ecdf(t,'censoring',censored);
Ступенчатые графики эмпирической функции распределения и границ доверительных интервалов.
>> stairs(x,f);
>> hold on;
>> stairs(x,flo,'r:');
>> stairs(x,fup,'r:');
Расчет значений теоретической функции распределения экспоненциального закона с параметром распределения равным 10 и построение общего графика для названных функций.
>> xx = 0:.1:max(t);
>> yy = 1-exp(-xx/10);
>> plot(xx,yy,'g-')
>> grid on
>> hold off;
fcdf- Функция распределения вероятностей закона Фишера
Синтаксис:
F = fcdf(X,V1,V2)
Описание:
fcdf(X,V1,V2) служит для расчета значения функции распределения вероятностей закона Фишера для параметров распределения V1, V2 и значения случайной величины X. Размерность векторов или матриц X, V1 и V2 должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов. Параметры V1 и V2 должны быть положительными целыми числами.
Функция распределения Фишера имеет вид
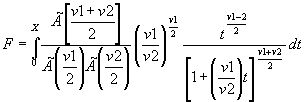 .
.
Результат расчета представляет собой значение вероятности F попадания случайной величины в интервал [0 X].
Примеры:
Использование скалярных аргументов X=0.5; V1=1; V2=2.
>> X=0.5
X =
0.5000
>> V1=1
V1 =
1
>> V2=2
V2 =
2
>> F = fcdf(X,V1,V2)
F =
0.4472
Использование векторного аргумента X=[0 1 2 3]; и скалярных параметров V1=1; V2=2.
>> X=[0 1 2 3]
X =
0 1 2 3
>> V1=1
V1 =
1
>> V2=2
V2 =
2
>> F = fcdf(X,V1,V2)
F =
0 0.5774 0.7071 0.7746
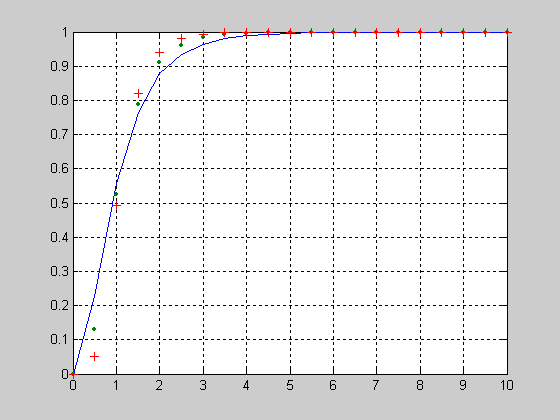
График функции распределения Фишера для параметров V1=[1 2 3]; V2=2.
>> X=0:1:10;
>> V1=5;
>> V2=20;
>> F1 = fcdf(X,V1,V2);
>> V1=10;
>> F2 = fcdf(X,V1,V2);
>> V1=25;
>> F3 = fcdf(X,V1,V2);
>> plot(X,F1,X,F2,'.',X,F3,'+')
>> grid on
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Вероятность попадания определяется по формуле ![]() .
.
Определение пределов.
>> xmin=1;
>> xmax=3;
Параметры распределения.
>> V1=2;
>> V2=5;
Расчет вероятности P попадания x в интервал [xmin xmax].
>> fcdf(xmax,V1,V2)- fcdf(xmin,V1,V2)
ans =
0.2919
logncdf - Функция распределения вероятностей логнормального закона
Синтаксис:
F = logncdf(x,mu,sigma)
Описание:
logncdf(x,mu,sigma) служит для расчета значения функции распределения вероятностей логнормального закона для параметров распределения mu (математического ожидания), sigma (среднего квадратического отклонения) и значения случайной величины х. Размерность векторов или матриц x, mu, sigma должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов.
Функция распределения вероятностей логнормального закона имеет вид
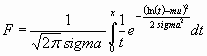 .
.
Примеры использования функции распределения вероятностей логнормального закона:
Использование скалярных аргументов x=0.5; mu=1; sigma=2.
>> x=0.5
x =
0.5000
>> mu=1
mu =
1
>> sigma=2
sigma =
2
>> F = logncdf(x,mu,sigma)
F =
0.1986
Использование векторного аргумента x=[0 0,3 0,6 0,9]; и скалярных параметров mu=1; sigma=2.
>> x=[0 0.3 0.6 0.9]
x =
0 0.3000 0.6000 0.9000
>> mu=1
mu =
1
>> sigma=2
sigma =
2
>> F = logncdf(x,mu,sigma)
F =
0 0.1352 0.2250 0.2902
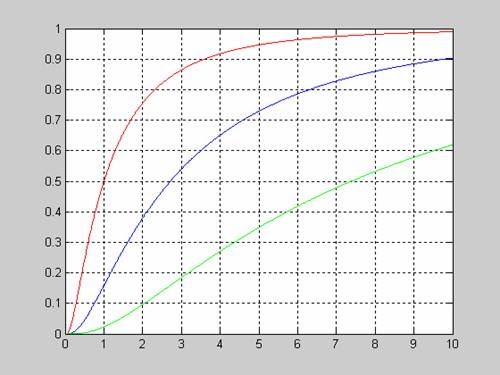
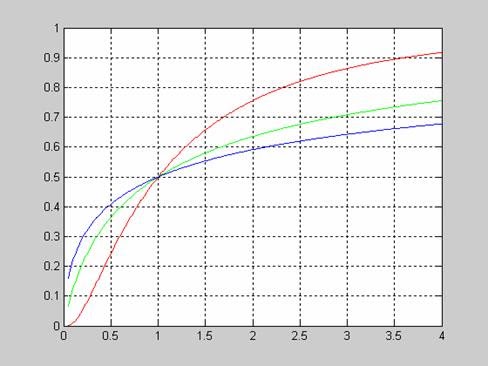
Рассмотрим вид функции распределения вероятностей логнормального закона в зависимости от значения mu при постоянном sigma=1.
>> x=0.05:0.01:10;
>> sigma=1;
>> mu=0;
>> f1 = logncdf(x,mu,sigma);
>> mu=1;
>> f2 = lognсdf(x,mu,sigma);
>> mu=2;
>> f3 = logncdf(x,mu,sigma);
>> plot(x,f1,'r',x,f2,'b',x,f3,'g')
>> grid on
Рассмотрим вид функции распределения вероятностей логнормального закона в зависимости от значения sigma при постоянном mu=0.
>> x=0.05:0.01:4;
>> mu=0;
>> sigma=1;
>> f1 = logncdf(x,mu,sigma);
>> sigma=2;
>> f2 = logncdf(x,mu,sigma);
>> sigma=3;
>> f3 = logncdf(x,mu,sigma);
>> plot(x,f1,'r',x,f2,'g',x,f3,'b')
>> grid on
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Вероятность попадания определяется по формуле ![]() .
.
Определение пределов интегрирования.
>> xmin=1;
>> xmax=3;
Параметры распределения.
>> mu=0;
>> sigma=1;
Расчет вероятности P попадания x в интервал [xmin xmax].
>> logncdf(xmax,mu,sigma) - logncdf(xmin,mu,sigma)
ans =
0.3640
nbincdf - Функция распределения вероятностей отрицательного биномиального закона
Синтаксис:
F = nbincdf(X,R,P)
Описание:
nbincdf(X,R,P) возвращает значение функции распределения вероятностей отрицательного биномиального закона для случайной величины Х, параметра R и вероятности появления события в одном опыте P. Размерность векторов или матриц X, R, P должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Функция распределения вероятностей отрицательного биномиального закона имеет вид
![]() ,
,
где ![]() - число сочетаний, которым можно выбрать i объектов из R+i-1,
- число сочетаний, которым можно выбрать i объектов из R+i-1, ![]() , q – вероятность обратного события, q=1-P.
, q – вероятность обратного события, q=1-P.
Простейшим случаем применения функции распределения вероятностей отрицательного биномиального закона является расчет вероятности появления некоторого события при независимых испытаниях с постоянной вероятностью появления события в одном опыте Р. Число дополнительных испытаний, которое должно быть проведено, чтобы получить заданное число R успешных попыток имеет отрицательное биномиальное распределение. Более общая трактовка отрицательного биномиального распределения позволяет задавать параметр R как положительное вещественное число. Для вещественного R коэффициент биномиального распределения рассчитывается как ![]() , где
, где ![]() - Гамма-функция.
- Гамма-функция.
Примеры использования функции распределения вероятностей отрицательного биномиального закона:
Использование скалярных аргументов X=2, R=10, P=0.5
>> X=2
X =
2
>> R=10
R =
10
>> P=0.5
P =
0.5000
>> F = nbincdf(X,R,P)
F =
0.0193
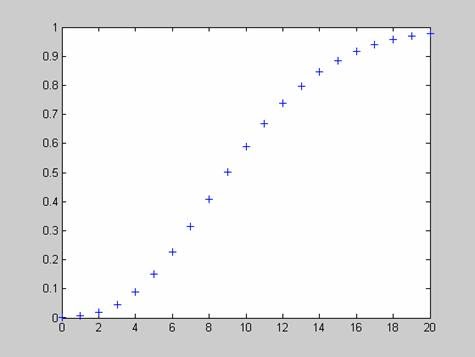
Расчет таблицы функции распределения для случайной величины X=[0 1 2 3 4 5 6 7 8 9] и аргументов R=10, P=0.5
>> X=0:1:20;
>> R=10;
>> P=0.5;
>> F = nbincdf(X,R,P);
>> [X' F']
ans =
0 0.0010
1.0000 0.0059
2.0000 0.0193
3.0000 0.0461
4.0000 0.0898
5.0000 0.1509
6.0000 0.2272
7.0000 0.3145
8.0000 0.4073
9.0000 0.5000
10.0000 0.5881
11.0000 0.6682
12.0000 0.7383
13.0000 0.7976
14.0000 0.8463
15.0000 0.8852
16.0000 0.9157
17.0000 0.9390
18.0000 0.9564
19.0000 0.9693
20.0000 0.9786
Графическое представление функции распределения
>> plot(X,f,'+')
ncfcdf- Функция распределения вероятностей смещенного закона Фишера
Синтаксис:
F = ncfcdf(X,NU1,NU2,DELTA)
Описание:
ncfcdf(X,NU1,NU2,DELTA)позволяет рассчитать значения функции распределения вероятностей смещенного закона Фишера для значений случайной величины Х, степеней свободы NU1, NU2 и положительного параметра смещения DELTA. Размерность векторов или матриц X, NU1, NU2, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
Функция распределения вероятностей определяется по формуле
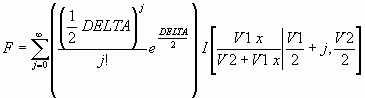 ,
,
где I(x|a,b) – неполная бета функция с параметрами a и b.
Примеры использования функции распределения вероятностей смещенного закона Фишера:
Использование скалярных аргументов X=0.1; NU1=5; NU2=8; DELTA=1.
>> X=0.1
X =
0.1000
>> NU1=5
NU1 =
5
>> NU2=8
NU2 =
8
>> DELTA=1
DELTA =
1
>> F = ncfcdf(X,NU1,NU2,DELTA)
F =
0.0068
Использование векторной случайной величины X=0:0.1:1 и скалярных аргументов NU1=5; NU2=8; DELTA=1.
>> X=0:0.1:1;
>> NU1=5;
>> NU2=8;
>> DELTA=1;
>> F = ncfpdf(X,NU1,NU2,DELTA);
>> [X' F']
ans =
0 0
0.1000 0.1555
0.2000 0.3243
0.3000 0.4448
0.4000 0.5172
0.5000 0.5518
0.6000 0.5595
0.7000 0.5490
0.8000 0.5269
0.9000 0.4980
1.0000 0.4656
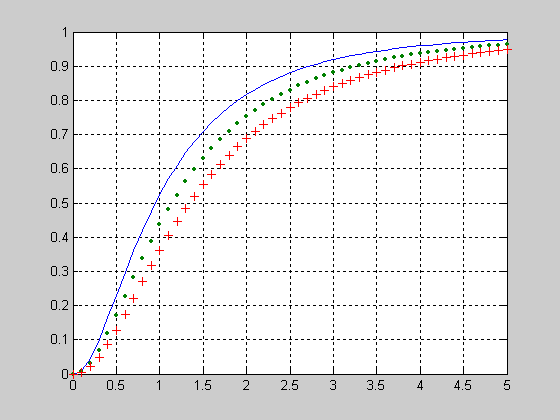
Исследование влияния коэффициента смещения DELTA=[0 1 2] на вид функции распределения вероятностей смещенного закона Фишера.
>> X=0:0.1:5;
>> NU1=5;
>> NU2=8;
>> DELTA=0;
>> f1 = ncfcdf(X,NU1,NU2,DELTA);
>> DELTA=1;
>> f2 = ncfcdf(X,NU1,NU2,DELTA);
>> DELTA=2;
>> f3 = ncfcdf(X,NU1,NU2,DELTA);
>> plot(X,f1,X,f2,'.',X,f3,'+')
>> grid on
nctcdf - Функция распределения вероятностей смещенного закона Стьюдента (смещенного t распределения)
Синтаксис:
F = nctcdf(X,NU,DELTA)
Описание:
nctcdf(X,NU,DELTA) позволяет рассчитать величину функции распределения вероятностей смещенного закона Стьюдента для значений случайной величины Х, степени свободы NU и параметра смещения DELTA. Размерность векторов или матриц X, NU, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Примеры использования функции распределения вероятностей смещенного закона Стьюдента:
Расчет вероятности попадания значения случайной величины Х в интервал ![]() . Вероятность попадания определяется по формуле
. Вероятность попадания определяется по формуле ![]() .
.
Определение границ интервала.
>> xmin=0;
>> xmax=2;
Параметры распределения.
>> NU =1;
>> DELTA =4;
Расчет вероятности P попадания Х в интервал [xmin xmax].
>> nctcdf(xmax,NU,DELTA)- nctcdf(xmin,NU,DELTA)
ans =
0.0736
Расчет вероятности попадания значения случайной величины Х в интервалы от ![]() до 0; 1; 2; 3.
до 0; 1; 2; 3.
>> X=[0 1 2 3];
>> NU =10;
>> DELTA =0;
>> F=nctcdf(X,NU,DELTA);
>> [X' F']
ans =
0 0.5000
1.0000 0.8296
2.0000 0.9633
3.0000 0.9933
Исследование влияния параметра смещения DELTA на вид функции распределения вероятностей смещенного закона Стьюдента при числе степеней свободы NU=5.
>> X=-5:0.1:5;
>> NU =5;
>> DELTA =0;
>> F1=nctcdf(X,NU,DELTA);
>> DELTA =1;
>> F2=nctcdf(X,NU,DELTA);
>> DELTA =2;
>> F3=nctcdf(X,NU,DELTA);
>> plot(X,F1, X,F2,'.', X,F3,':')
>> grid on
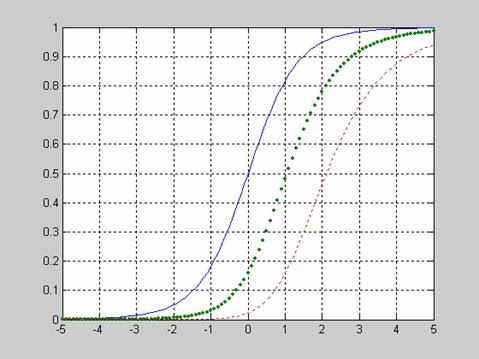
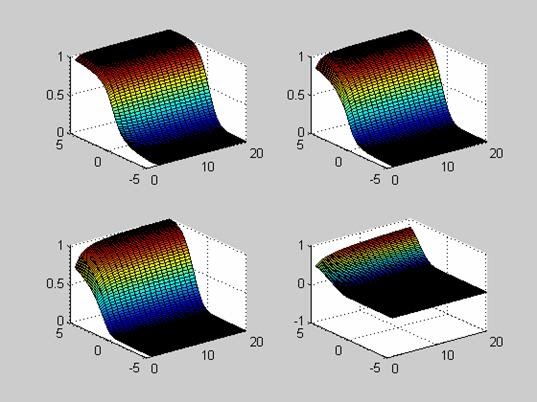
Исследование влияния числа степеней свободы NU и параметра смещения DELTA на вид функции распределения.
>> [NU X] = meshgrid([1:1:20], [-5:0.1:5]);
>> DELTA=0;
>> F=nctcdf(X,NU,DELTA);
>> subplot(2,2,1)
>> surf(NU,X,F)
>> DELTA=1;
>> F=nctcdf(X,NU,DELTA);
>> subplot(2,2,2)
>> surf(NU,X,F)
>> DELTA=2;
>> F=nctcdf(X,NU,DELTA);
>> subplot(2,2,3)
>> surf(NU,X,F)
>> DELTA=4;
>> F=nctcdf(X,NU,DELTA);
>> subplot(2,2,4)
>> surf(NU,X,F)
ncx2cdf - Функция вероятностей смещенного распределения хи-квадрат
Синтаксис:
F = ncx2cdf(X,V,DELTA)
Описание:
ncx2cdf(X,V,DELTA) служит для расчета значений функции вероятностей смещенного распределения хи-квадрат для значений случайной величины Х, степени свободы V и параметра смещения DELTA. Размерность векторов или матриц X, V, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
В некоторых литературных источниках это распределение называется обобщенным законом Релея, законом Релея-Райса, распределением Райса.
Примеры использования функции вероятностей смещенного распределения хи-квадрат:
Расчет вероятности попадания значения случайной величины Х в интервал ![]() . Вероятность попадания определяется по формуле
. Вероятность попадания определяется по формуле ![]() .
.
Определение границ интервала.
>> xmin=1;
>> xmax=2;
Параметры распределения.
>> V =10;
>> DELTA =2;
Расчет вероятности P попадания Х в интервал [xmin xmax].
>> ncx2cdf(xmax,V,DELTA) - ncx2cdf(xmin,V,DELTA)
ans =
0.0015
Расчет вероятности попадания значения случайной величины Х в интервалы от ![]() до 0; 1; 2; 3.
до 0; 1; 2; 3.
>> X=[0 1 2 3];
>> V =10;
>> DELTA =1;
>> F= ncx2cdf(X,V,DELTA);
>> [X' F']
ans =
0 0
1.0000 0.0001
2.0000 0.0024
3.0000 0.0127
Исследование влияния числа степеней свободы V и параметра смещения DELTA на вид функции распределения вероятностей хи-квадрат.
>> X=0:0.1:20;
>> V =5;
>> DELTA =0;
>> F1=ncx2cdf (X,V,DELTA);
>> DELTA =1;
>> F2=ncx2cdf (X,V,DELTA);
>> DELTA =2;
>> F3= ncx2cdf (X,V,DELTA);
>> subplot(2,2,1)
>> plot(X,F1, X,F2,'.', X,F3,':')
>> grid on
Вид поверхности функции распределения вероятностей хи-квадрат в зависимости от параметров V, DELTA.
>> [V X] = meshgrid([1:1:20], [0:0.5:20]);
>> DELTA=0;
>> F=ncx2cdf (X,V,DELTA);
>> subplot(2,2,2)
>> surf(V,X,F)
>> DELTA=2;
>> F=ncx2cdf (X,V,DELTA);
>> subplot(2,2,3)
>> surf(V,X,F)
>> DELTA=5;
>> F=ncx2cdf (X,V,DELTA);
>> subplot(2,2,4)
>> surf(V,X,F)
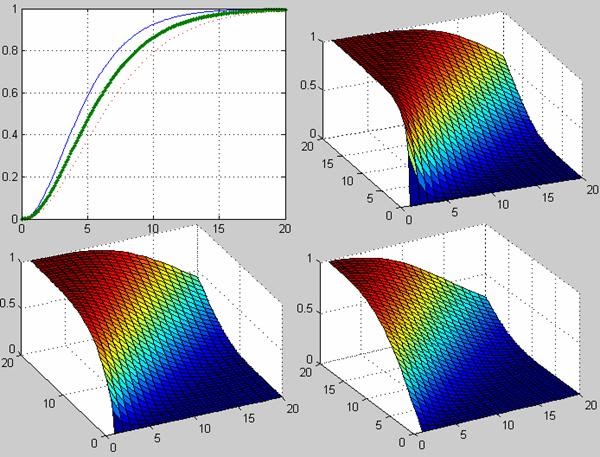
normcdf - Функция распределения вероятностей нормального закона
Синтаксис:
F = normcdf(X,MU,SIGMA)
Описание:
normcdf(X,MU,SIGMA) служит для расчета значений функции распределения вероятностей нормального закона для значений случайной величины Х, математического ожидания MU и среднего квадратического отклонения SIGMA. Размерность векторов или матриц X, MU, SIGMA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение среднего квадратического отклонения SIGMA должно быть положительным.
Функция распределения вероятностей нормального закона имеет вид
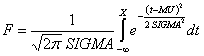 .
.
Величина F представляет собой вероятность падания случайной величины в интервал ![]() .
.
Стандартное нормальное распределение имеет параметры распределения равные MU=0 и SIGMA=1.
Примеры использования функции распределения вероятностей нормального закона:
Расчет вероятности попадания значения случайной величины Х, распределенной по закону стандартизованного нормального распределения, в интервал ![]() .
.
Определение границ интервала.
>> xmin=1;
>> xmax=2;
Параметры распределения.
>> MU =0;
>> SIGMA =1;
Расчет вероятности P попадания Х в интервал [xmin xmax].
>> normcdf(xmax,MU,SIGMA) - normcdf(xmin,MU,SIGMA)
ans =
0.1359
Расчет вероятности попадания значения случайной величины Х в интервалы ![]() ,
, ![]() ,
, ![]() .
.
>> X=[1 2 3];
>> MU =0;
>> SIGMA =1;
>> F= 2* (normcdf(X,MU,SIGMA) - normcdf(0,MU,SIGMA));
>> [X' F']
ans =
1.0000 0.6827
2.0000 0.9545
3.0000 0.9973
Исследование влияния параметров MU, SIGMA на вид функции распределения вероятностей нормального закона.
>> X=-5:0.1:5;
>> MU =0;
>> SIGMA =1;
>> F1= normcdf(X,MU,SIGMA);
>> SIGMA =2;
>> F2= normcdf(X,MU,SIGMA);
>> SIGMA =3;
>> F3= normcdf(X,MU,SIGMA);
>> subplot(2,2,1)
>> plot(X,F1, X,F2,'.', X,F3,':')
>> grid on
Вид поверхности функции распределения вероятностей нормального закона в зависимости от параметров MU, SIGMA.
>> [X SIGMA] = meshgrid([-5:0.1:5], [1:2/20:3]);
>> MU =0;
>> F= normcdf(X,MU,SIGMA);
>> subplot(2,2,2)
>> surf(X,SIGMA,F)
>> MU =2;
>> F= normcdf(X,MU,SIGMA);
>> subplot(2,2,3)
>> surf(X,SIGMA,F)
>> MU =4;
>> F= normcdf(X,MU,SIGMA);
>> subplot(2,2,4)
>> surf(X,SIGMA,F)
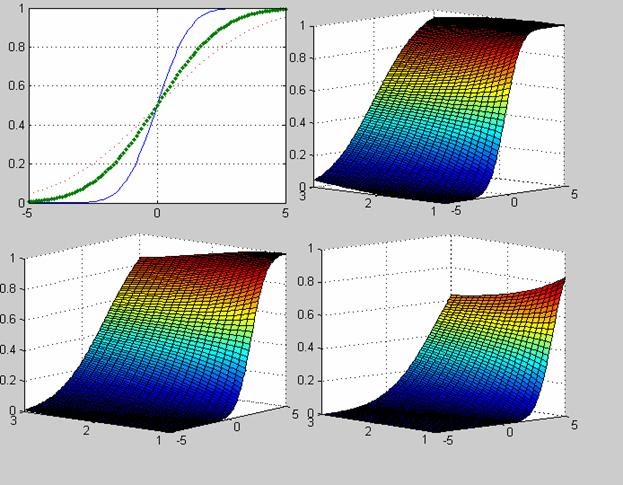
poisscdf - Функция распределения вероятностей закона Пуассона
Синтаксис:
F = poisscdf(X,LAMBDA)
Описание:
poisscdf(X,LAMBDA) позволяет рассчитать значение функции распределения вероятностей закона Пуассона для случайной величины Х и параметра LAMBDA. Размерность векторов или матриц X, LAMBDA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение параметра LAMBDA должно быть положительным.
Функция распределения вероятностей Пуассона имеет вид
![]()
![]() .
.
Примеры использования функции распределения вероятностей:
Расчет вероятности попадания значения случайной величины Х в интервал [2 3].
Определение границ интервала.
>> xmin=2;
>> xmax=3;
Параметр распределения.
>> LAMBDA =5;
Расчет вероятности попадания Х в интервал [xmin xmax].
>> poisscdf(xmax,LAMBDA) - poisscdf(xmin,LAMBDA)
ans =
0.1404
Расчет вероятности попадания значения случайной величины Х в интервалы от ![]() до 0; 1; 2; 3.
до 0; 1; 2; 3.
>> X=[0 1 2 3];
>> LAMBDA =5;
>> F= poisscdf(X,LAMBDA);
>> [X' F']
ans =
0 0.0067
2.0000 0.1247
1.0000 0.0404
3.0000 0.2650
Рассмотрим решение задачи. Технологический процесс производства жестких магнитных носителей останавливается при наличии 4 и более сбойных секторов. Определить какова вероятность остановки процесса, если среднее число бракованных секторов равно 2.
Вероятность остановки процесса определяется как вероятность обратного события P, состоящего в том, что число бракованных секторов превысит критическое значение X=4 при среднем числе отказов LAMBDA=2.
>> X=4;
>> LAMBDA =2;
>> P= 1 - poisscdf(X, LAMBDA)
P =
0.0527
Исследование влияния параметра LAMBDA на вид функции распределения вероятностей закона Пуассона.
>> X=0:1:20;
>> LAMBDA =2;
>> F1= poisscdf(X,LAMBDA);
>> LAMBDA =5;
>> F2= poisscdf(X,LAMBDA);
>> LAMBDA =10;
>> F3 = poisscdf(X,LAMBDA);
>> plot(X,F1,'g', X,F2,'r', X,F3,'b')
>> grid on
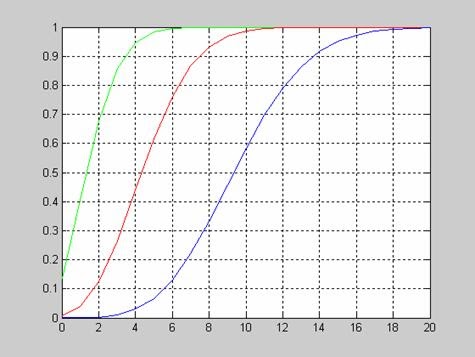
raylcdf - Функция распределения вероятностей закона Релея
Синтаксис:
F = raylcdf(X,B)
Описание:
raylcdf(X,B) служит для расчета значений функции распределения вероятностей закона Релея для случайной величины Х и параметра B. Размерность векторов или матриц X, B должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Функция распределения вероятностей закона Релея имеет вид
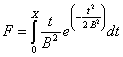 .
.
Примеры использования функции распределения вероятностей закона Релея:
Расчет вероятности попадания значения случайной величины Х в интервал [2 5].
Определение границ интервала.
>> xmin=2;
>> xmax=5;
Параметр распределения.
>> B = 5;
Расчет вероятности попадания Х в интервал [xmin xmax].
>> raylcdf(xmax,B)- raylcdf(xmin,B)
ans =
0.3166
Расчет вероятности попадания значения случайной величины Х в интервалы от 0 до 5; 6; 7; 8, при В=10.
>> X=[5 6 7 8];
>> B = 10;
>> F= raylcdf (X,B);
>> [X' F']
ans =
5.0000 0.1175
6.0000 0.1647
7.0000 0.2173
8.0000 0.2739
Исследование влияния параметра LAMBDA на вид функции распределения вероятностей закона Релея.
>> X=0:1:20;
>> B =2;
>> F1= raylcdf (X,B);
>> B =5;
>> F2= raylcdf (X,B);
>> B =10;
>> F3 = raylcdf (X,B);
>> plot(X,F1,'g', X,F2,'r', X,F3,'b')
>> grid on
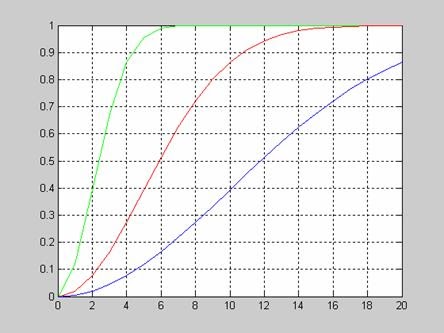
tcdf - Функция распределения вероятностей закона Стьюдента
Синтаксис:
F = tcdf(X,V)
Описание:
tcdf(X,V) служит для расчета значений функции распределения вероятностей закона Стьюдента для значений случайной величины Х и степени свободы V. Размерность векторов или матриц X, V должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение числа степеней свободы V должно быть положительным целым числом.
Вид функции распределения вероятностей закона Стьюдента
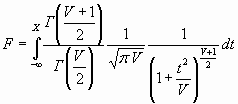 .
.
Результатом расчета по приведенной формуле является вероятность попадания случайной величины в интервал (-∞ Х] для заданной величины числа степеней свободы.
Примеры использования функции распределения вероятностей:
Расчет вероятности попадания значения случайной величины Х в интервал [2 3].
Определение границ интервала.
>> xmin=2;
>> xmax=3;
Параметр распределения.
>> V =5;
Расчет вероятности попадания Х в интервал [xmin xmax].
>> tcdf(xmax,V) - tcdf(xmin,V)
ans =
0.0359
Расчет вероятности попадания значения случайной величины Х в интервалы от ![]() до 0; 1; 2; 3.
до 0; 1; 2; 3.
>> X=[0 1 2 3];
>> V =5;
>> F= tcdf (X,V);
>> [X' F']
ans =
0 0.5000
1.0000 0.8184
2.0000 0.9490
3.0000 0.9850
Рассмотрим решение задачи. В 10 пробах пива обнаружено среднее содержание этилового спирта 5,5% на единицу объема со средним квадратическим отклонением 0,5%. Какова вероятность, что действительное содержание этилового спирта менее 5%.
Стандартизованное значение случайной величины – объемной доли спирта составляет
>> t = (5.0 - 5.5) / 0.5;
Вероятность попадания случайной величины в интервал от 0,5% до 5,5% составляет
>> probability = tcdf(t,10 - 1)
0.1717
betapdf- Функции плотности вероятности бета распределения
Синтаксис:
f = betapdf(x,a,b)
Описание:
f = betapdf(x,a,b) предназначена для расчета значения функции плотности вероятности бета распределения для параметров распределения a, b и значения случайной величины x. Размерность векторов или матриц x, a и b должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Параметры a и b должны быть положительными. Значение случайной величины x должно находиться в интервале [0 1].
Функция плотности вероятности бета распределения имеет вид
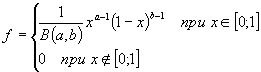 ,
,
где ![]() - Бета функция.
- Бета функция.
Выходной параметр f представляет собой значение функции плотности вероятности бета распределения для сочетания значений случайной величины x и параметров a, b. В частном случае при a=1 и b=1 бета распределение вырождается в равномерное.
Примеры:
Использование скалярных аргументов x=0.5; a=1; b=2.
>> x=0.5
x =
0.5000
>> a=1
a =
1
>> b=2
b =
2
>> f = betapdf(x,a,b)
f =
1
Использование векторного аргумента x=[0 0,3 0,6 0, 9]; и скалярных параметров a=1; b=2.
>> x=0:0.3:1
x =
0 0.3000 0.6000 0.9000
>> a=1
a =
1
>> b=2
b =
2
>> f = betapdf(x,a,b)
f =
0 1.4000 0.8000 0.2000
Использование матричных аргумента x, параметра a и скалярного параметра b.
Определение матрицы x.
>> x=0:0.1:1
x =
Columns 1 through 6
0 0.1000 0.2000 0.3000 0.4000 0.5000
Columns 7 through 11
0.6000 0.7000 0.8000 0.9000 1.0000
>> x=[x' x' x' x' x']
x =
0 0 0 0 0
0.1000 0.1000 0.1000 0.1000 0.1000
0.2000 0.2000 0.2000 0.2000 0.2000
0.3000 0.3000 0.3000 0.3000 0.3000
0.4000 0.4000 0.4000 0.4000 0.4000
0.5000 0.5000 0.5000 0.5000 0.5000
0.6000 0.6000 0.6000 0.6000 0.6000
0.7000 0.7000 0.7000 0.7000 0.7000
0.8000 0.8000 0.8000 0.8000 0.8000
0.9000 0.9000 0.9000 0.9000 0.9000
1.0000 1.0000 1.0000 1.0000 1.0000
Определение матрицы a.
>> a=ones(1,11)'
a =
1
1
1
1
1
1
1
1
1
1
1
>> a=[a*2 a*4 a*6 a*8 a*10]
a =
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
Задание скаляра b.
>> b=5
b =
5
Расчет матрицы функции плотности вероятности бета распределения f.
>> f = betapdf(x,a,b)
f =
0 0 0 0 0
1.9683 0.1837 0.0083 0.0003 0.0000
2.4576 0.9175 0.1652 0.0208 0.0021
2.1609 1.8152 0.7351 0.2079 0.0473
1.5552 2.3224 1.6722 0.8409 0.3401
0.9375 2.1875 2.4609 1.9336 1.2219
0.4608 1.5483 2.5082 2.8379 2.5825
0.1701 0.7779 1.7153 2.6416 3.2719
0.0384 0.2294 0.6606 1.3288 2.1496
0.0027 0.0204 0.0744 0.1894 0.3878
0 0 0 0 0
Рассмотрим изменение вида функции плотности вероятности бета распределения в зависимости от значения параметров a и b.
Сформируем матрицу x.
>> x=0:0.01:1;
>> x=[x' x' x' x' x'];
Определение матрицы a. Значения параметра a изменяется в последовательности 2, 4, 6, 8, 10.
>> a=ones(1,101)';
>> a=[a*2 a*4 a*6 a*8 a*10];
Функция плотности вероятности бета распределения для заданной последовательности a и значения параметра b=2.
>> b=2;
>> f = betapdf(x,a,b);
>> plot(x,f)
>> grid on
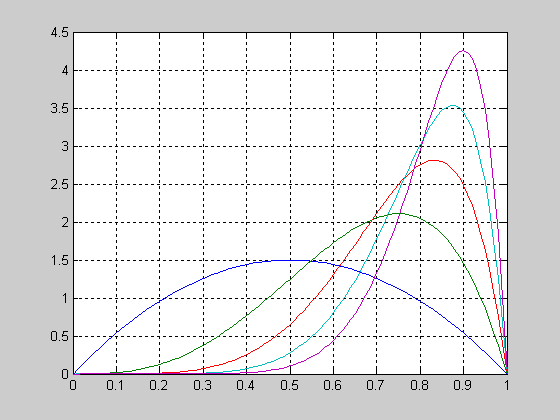
Вид функции плотности вероятности бета распределения для заданной последовательности a и значения параметра b=8
>> b=8;
>> f = betapdf(x,a,b);
>> plot(x,f)
>> grid on
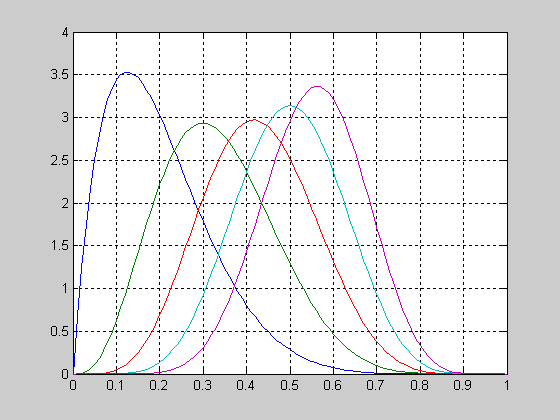
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Вероятность попадания определяется по формуле 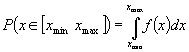 .
.
Определение пределов интегрирования.
>> xmin=0.1;
>> xmax=0.2;
Параметры бета распределения.
>> a=1;
>> b=4;
Расчет вероятности P попадания x в интервал [xmin xmax].
>> P=quad('betapdf',xmin,xmax,1.e-6,0,a,b)
P =
0.2465
binopdf - Функции плотности вероятности биномиального распределения
Синтаксис:
f = binopdf(x,n,p)
Описание:
f = binopdf(x,n,p) служит для расчета значения функции плотности вероятности биномиального распределения для значения случайной величины x и параметров n, p. Размерность векторов или матриц x, n и p должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов.
Значение параметра n должно быть положительным целым. Значение параметра p должно находиться в интервале [0 1]. Значение случайной величины x должно быть целым, положительным и ![]() .
.
Функция плотности вероятности биномиального распределения имеет вид
![]() ,
,
где ![]() - число сочетаний, которым можно выбрать x объектов из n,
- число сочетаний, которым можно выбрать x объектов из n, ![]() ,
,
![]() - вероятность появления события в отдельном опыте,
- вероятность появления события в отдельном опыте,
![]() - вероятность отсутствия события в отдельном опыте.
- вероятность отсутствия события в отдельном опыте.
Выходной параметр f представляет собой значение вероятности появления некоторого события x раз при n независимых испытаниях.
Примеры:
Использование скалярных аргументов x=5; n=10; p=0.7.
>> x=5
x =
5
>> n=10
n =
10
>> p=0.7
p =
0.7000
>> f = binopdf(x,n,p)
f =
0.1029
Использование векторного аргумента x=[1 2 3 4 5]; и скалярных параметров n=10; p=0.7.
>> x=1:5
x =
1 2 3 4 5
>> n=10
n =
10
>> p=0.7
p =
0.7000
>> f = binopdf(x,n,p)
f =
0.0001 0.0014 0.0090 0.0368 0.1029
Использование матричных аргумента x, параметра p и скалярного параметра n.
Определение матрицы x.
>> x=1:5
x =
1 2 3 4 5
>> x=[x' x' x' x' x']
x =
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
Определение матрицы вероятностей появления события p в одном опыте.
>> p=ones(1,5)
p =
1 1 1 1 1
>> p=p'
p =
1
1
1
1
1
>> p=[p*0.1 p*0.3 p*0.5 p*0.7 p*0.9]
p =
0.1000 0.3000 0.5000 0.7000 0.9000
0.1000 0.3000 0.5000 0.7000 0.9000
0.1000 0.3000 0.5000 0.7000 0.9000
0.1000 0.3000 0.5000 0.7000 0.9000
0.1000 0.3000 0.5000 0.7000 0.9000
Задание скаляра n.
>> n=10
n =
10
Расчет матрицы значений функции плотности вероятности биномиального распределения f.
>> f = binopdf(x,n,p)
f =
0.3874 0.1211 0.0098 0.0001 0.0000
0.1937 0.2335 0.0439 0.0014 0.0000
0.0574 0.2668 0.1172 0.0090 0.0000
0.0112 0.2001 0.2051 0.0368 0.0001
0.0015 0.1029 0.2461 0.1029 0.0015
Рассмотрим изменение вида функции плотности вероятности биномиального распределения для заданной последовательности p и значения параметра n=50.
Сформируем матрицу x.
>> x=1:30;
>> x=[x' x' x' x' x'];
Сформируем матрицу p. Значения параметра p будут меняться в последовательности 0,2; 0,3; 0,4; 0,5; 0,6.
>> p=ones(1,30)';
>> p=[p*0.2 p*0.3 p*0.4 p*0.5 p*0.6];
Рассмотрим вид функции плотности вероятности биномиального распределения для заданной последовательности p и значения параметра n=50.
>> n=50;
>> f = binopdf(x,n,p);
>> plot(x,f)
>> grid on
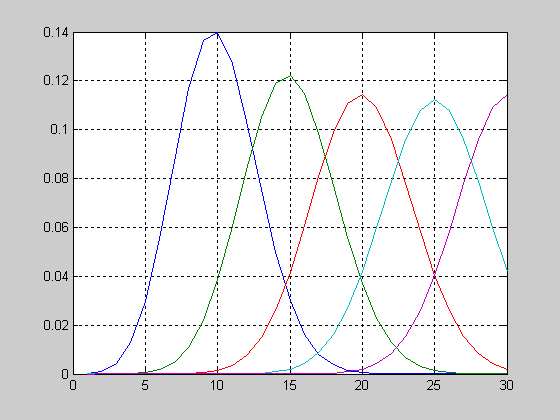
Рассмотрим решение с помощью Statistics Toolbox классической задачи из курса теории вероятностей.
Выполняется контроль качества 200 изделий по одному параметру в день. Известно, что 2% изделий бракованные. Какова вероятность не обнаружить ни одного дефекта при контроле.
Вероятность обнаружения заданного количества дефектов определяется по формуле
![]() ,
,
где n=200;
p=0,02;
q=1-p=0,98;
x=0.
Подставим указанные значения в функцию binopdf
>> f=binopdf(0,200,0.02)
f =
0.0176
Каково наиболее вероятное значение i обнаруженных дефектов?
f = binopdf([0:200],200,0.02);
[x,i] = max(y);
i
i =
5
chi2pdf - Функция плотности вероятности распределения хи-квадрат
Синтаксис:
f = chi2pdf(x,v)
Описание:
f = chi2pdf(x,v) вычисляет значение функции плотности вероятности распределения ![]() для параметра распределения v и значения случайной величины x. Размерность векторов или матриц x и v должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Размерность f соответствует максимальной размерности x или v. v – число степеней свободы, целое положительное число.
для параметра распределения v и значения случайной величины x. Размерность векторов или матриц x и v должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Размерность f соответствует максимальной размерности x или v. v – число степеней свободы, целое положительное число.
Функция плотности вероятности распределения ![]() имеет вид
имеет вид
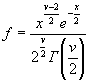 ,
,
где ![]() - Гамма-функция.
- Гамма-функция.
Выходной параметр f представляет собой значение плотности вероятности распределения ![]() соответствующее числу степеней свободы v и значению случайной величины x.
соответствующее числу степеней свободы v и значению случайной величины x.
Если x является стандартизованной случайной величиной распределенной по нормальному закону, то случайная величина ![]() распределена по закону
распределена по закону ![]() с числом степеней свободы v=1. Сумма квадратов n стандартизованных случайных величин распределенных по нормальному закону x1, x2, …, xn имеет распределение
с числом степеней свободы v=1. Сумма квадратов n стандартизованных случайных величин распределенных по нормальному закону x1, x2, …, xn имеет распределение ![]() с числом степеней свободы v=n.
с числом степеней свободы v=n.
Примеры:
Использование скалярных аргументов x=0.1; v=10.
>> v=10
v =
10
>> x=0.1
x =
0.1000
>> f = chi2pdf(x,v)
f =
1.2386e-007
Использование векторного аргумента x=[0 0,3 0,6 0, 9]; и скалярного параметра v=10.
>> x=[0 0.3 0.6 0.9]
x =
0 0.3000 0.6000 0.9000
>> v=10
v =
10
>> f = chi2pdf(x,v)
f =
1.0e-003 *
0 0.0091 0.1250 0.5447
Использование матричного аргумента x и скалярного параметра v.
Определение матрицы x.
>> x=0:0.1:1
x =
Columns 1 through 5
0 0.1000 0.2000 0.3000 0.4000
Columns 6 through 10
0.5000 0.6000 0.7000 0.8000 0.9000
Column 11
1.0000
>> x=[x' x' x' x' x']
x =
0 0 0 0 0
0.1000 0.1000 0.1000 0.1000 0.1000
0.2000 0.2000 0.2000 0.2000 0.2000
0.3000 0.3000 0.3000 0.3000 0.3000
0.4000 0.4000 0.4000 0.4000 0.4000
0.5000 0.5000 0.5000 0.5000 0.5000
0.6000 0.6000 0.6000 0.6000 0.6000
0.7000 0.7000 0.7000 0.7000 0.7000
0.8000 0.8000 0.8000 0.8000 0.8000
0.9000 0.9000 0.9000 0.9000 0.9000
1.0000 1.0000 1.0000 1.0000 1.0000
Определение числа степеней свободы v=5.
>> v=5
v =
5
Расчет матрицы функции плотности вероятности распределения хи-квадрат.
>> f = chi2pdf(x,v)
f =
0 0 0 0 0
0.0040 0.0040 0.0040 0.0040 0.0040
0.0108 0.0108 0.0108 0.0108 0.0108
0.0188 0.0188 0.0188 0.0188 0.0188
0.0275 0.0275 0.0275 0.0275 0.0275
0.0366 0.0366 0.0366 0.0366 0.0366
0.0458 0.0458 0.0458 0.0458 0.0458
0.0549 0.0549 0.0549 0.0549 0.0549
0.0638 0.0638 0.0638 0.0638 0.0638
0.0724 0.0724 0.0724 0.0724 0.0724
0.0807 0.0807 0.0807 0.0807 0.0807
Рассмотрим как изменяется вид функции плотности вероятности распределения хи-квадрат в зависимости от изменения значения числа степеней свободы v.
Сформируем матрицу x.
x=0:0.01:10;
x=[x' x' x' x' x'];
Сформируем матрицу v. Значения параметра v будут меняться в последовательности 2, 4, 6, 8, 10.
v=ones(1,1001)';
v=[v*2 v*4 v*6 v*8 v*10];
Рассмотрим вид функции плотности вероятности распределения хи-квадрат для заданной последовательности v.
f = chi2pdf(x,v)
plot(x,f)
grid on
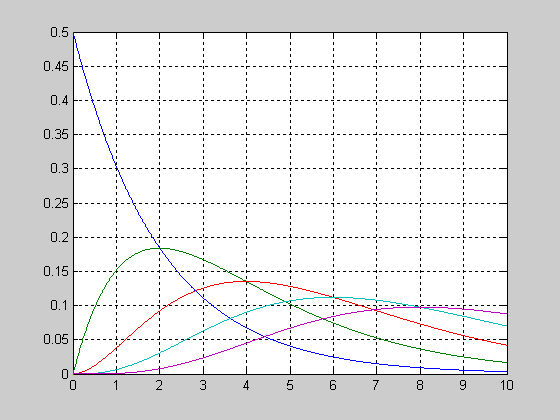
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Расчет ведется по формуле .gif) .
.
Определим пределы интегрирования.
>> xmin=0.1;
>> xmax=2;
Зададим число степеней свободы распределения хи-квадрат.
>> v=5;
Рассчитаем вероятность P попадания x в интервал [xmin xmax].
>> P=quad('chi2pdf',xmin,xmax,1.e-6,0,v)
P =
0.1507
exppdf - Функция плотности вероятности экспоненциального распределения
Синтаксис:
f = exppdf(x,mu)
Описание:
f = exppdf(x,mu) служит для расчета значения функции плотности вероятности экспоненциального распределения для параметра распределения ![]() (mu) и значения случайной величины x. Размерность векторов или матриц x и v должна быть одинаковой. Размерность скалярного параметра увеличивается до размера другого входного аргумента. Параметр
(mu) и значения случайной величины x. Размерность векторов или матриц x и v должна быть одинаковой. Размерность скалярного параметра увеличивается до размера другого входного аргумента. Параметр ![]() (mu) должен быть положительным числом.
(mu) должен быть положительным числом.
Функция плотности вероятности экспоненциального распределения имеет вид
![]() .
.
Экспоненциальное распределение можно рассматривать как гамма распределение с первым параметром равным единице.
Экспоненциальное распределение используется при моделировании времени ожидания некоторого события, когда вероятность его появления не зависит от времени ожидания прошедшего до текущего момента. Например, вероятность разрушения спирали лампы накаливания в следующий момент времени не зависит от времени ее эксплуатации.
Примеры:
Использование скалярных аргументов x=5; mu=2.
>> mu=2
mu =
2
>> x=5
x =
5
>> f = exppdf(x,mu)
f =
0.0410
Использование векторного аргумента x=[0 3 6 9]; и скалярного параметра mu=2.
>> mu=2
mu =
2
>> x=[0 3 6 9]
x =
0 3 6 9
>> f = exppdf(x,mu)
f =
0.5000 0.1116 0.0249 0.0056
Использование матричного аргумента x и скалярного параметра mu.
Определение матрицы x.
>> x=0:1:10
x =
0 1 2 3 4 5 6 7 8 9 10
>> x=[x' x' x' x' x']
x =
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
6 6 6 6 6
7 7 7 7 7
8 8 8 8 8
9 9 9 9 9
10 10 10 10 10
Определение числа степеней свободы mu=5.
>> mu=5
mu =
5
Расчет матрицы функции плотности вероятности экспоненциального распределения.
>> f = exppdf(x,mu)
f =
0.2000 0.2000 0.2000 0.2000 0.2000
0.1637 0.1637 0.1637 0.1637 0.1637
0.1341 0.1341 0.1341 0.1341 0.1341
0.1098 0.1098 0.1098 0.1098 0.1098
0.0899 0.0899 0.0899 0.0899 0.0899
0.0736 0.0736 0.0736 0.0736 0.0736
0.0602 0.0602 0.0602 0.0602 0.0602
0.0493 0.0493 0.0493 0.0493 0.0493
0.0404 0.0404 0.0404 0.0404 0.0404
0.0331 0.0331 0.0331 0.0331 0.0331
0.0271 0.0271 0.0271 0.0271 0.0271
Рассмотрим как меняется вид функции плотности вероятности экспоненциального распределения в зависимости от изменения параметра mu.
Сформируем матрицу x
>> x=0:0.1:10;
>> x=[x' x' x' x' x'];
Сформируем матрицу mu. Значения параметра mu будут меняться в последовательности 2, 4, 6, 8, 10.
>> mu=ones(1,101)';
>> mu=[mu*2 mu*4 mu*6 mu*8 mu*10];
Рассмотрим вид функции плотности вероятности экспоненциального распределения для заданной последовательности значений mu.
>> f = exppdf(x,mu);
>> plot(x,f)
>> grid on
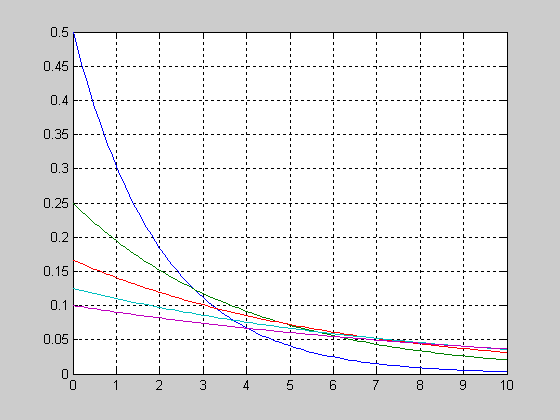
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Расчет выполняется по формуле .gif) .
.
Определим пределы интегрирования.
>> xmin=1;
>> xmax=2;
Зададим значение параметра mu экспоненциального распределения.
>> mu=5;
Расчет вероятности P попадания x в интервал [xmin xmax].
>> P=quad('exppdf',xmin,xmax,1.e-6,0,mu)
P =
0.1484
fpdf - Функция плотности вероятности распределения Фишера
Синтаксис:
f = fpdf(x,v1,v2)
Описание:
f = fpdf(x,v1,v2) служит для расчета значения функции плотности вероятности распределения Фишера для параметров распределения v1, v2 и значения случайной величины x. Размерность векторов или матриц x, v1 и v2 должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов. Параметры v1 и v2 должны быть положительными целыми. Значение случайной величины x должно находиться в интервале ![]() .
.
Функция плотности вероятности распределения Фишера имеет вид
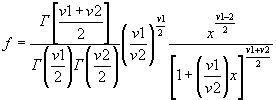 .
.
Примеры:
Использование скалярных аргументов x=0.5; v1=1; v2=2.
>> x=0.5
x =
0.5000
>> v1=1
v1 =
1
>> v2=2
v2 =
2
>> f = fpdf(x,v1,v2)
f =
0.3578
Использование векторного аргумента x=[0 0,3 0,6 0, 9]; и скалярных параметров v1=1; v2=2.
>> v1=1
v1 =
1
>> v2=2
v2 =
2
>> x=[0 3 6 9]
x =
0 3 6 9
>> f = fpdf(x,v1,v2)
f =
0 0.0516 0.0180 0.0091
Использование матричных аргумента x, параметра v1 и скалярного параметра v2.
Определение матрицы x.
>> x=0:1:10
x =
0 1 2 3 4 5 6 7 8 9 10
>> x=[x' x' x' x' x']
x =
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
6 6 6 6 6
7 7 7 7 7
8 8 8 8 8
9 9 9 9 9
10 10 10 10 10
Определение матрицы v1.
>> v1=ones(1,11)'
v1 =
1
1
1
1
1
1
1
1
1
1
1
>> v1=[v1*2 v1*4 v1*6 v1*8 v1*10]
v1 =
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
Задание скаляра v2.
>> v2=5
v2 =
5
Расчет матрицы функции плотности вероятности распределения Фишера f.
>> f = fpdf(x,v1,v2)
f =
0 0 0 0 0
0.3080 0.3976 0.4451 0.4749 0.4955
0.1278 0.1520 0.1624 0.1682 0.1719
0.0633 0.0682 0.0693 0.0697 0.0698
0.0353 0.0351 0.0344 0.0339 0.0335
0.0214 0.0200 0.0191 0.0185 0.0181
0.0138 0.0123 0.0115 0.0111 0.0108
0.0093 0.0080 0.0074 0.0070 0.0068
0.0066 0.0055 0.0050 0.0047 0.0045
0.0048 0.0039 0.0035 0.0033 0.0032
0.0036 0.0028 0.0025 0.0024 0.0023
Рассмотрим изменение вида функции плотности вероятности распределения Фишера в зависимости от значений чисел степеней свободы v1 и v2.
Сформируем матрицу x.
>> x=0:0.1:10;
>> x=[x' x' x' x' x'];
Сформируем матрицу v1. Значения параметра v1 будут меняться в последовательности 2, 4, 6, 8, 10.
>> v1=ones(1,101)';
>> v1=[v1*2 v1*4 v1*6 v1*8 v1*10];
Рассмотрим вид функции плотности вероятности распределения Фишера для заданной последовательности v1 и значения параметра v2=5.
>> v2=5;
>> f = fpdf(x,v1,v2);
>> plot(x,f)
>> grid on
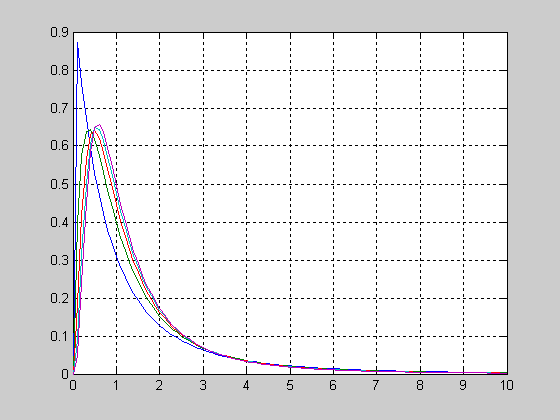
Вид функции плотности вероятности распределения Фишера для заданной последовательности v1 и значения параметра v2=2.
>> v2=2;
>> f = fpdf(x,v1,v2);
>> plot(x,f)
>> grid on
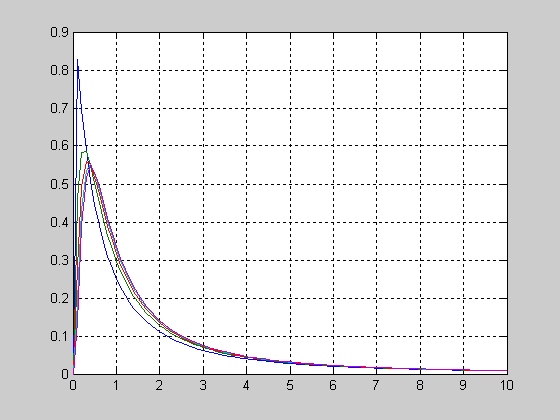
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. Расчет ведется по формуле .gif) .
.
Определим пределы интегрирования.
>> xmin=0.1;
>> xmax=2;
Зададим параметры распределения Фишера.
>> v1=2;
>> v2=4;
Рассчитаем вероятность P попадания x в интервал [xmin xmax].
>> P=quad('fpdf',xmin,xmax,1.e-6,0,v1,v2)
P =
0.6570
gampdf - Функция плотности вероятности гамма распределения
Синтаксис:
f = gampdf(x,a,b)
Описание:
f = gampdf(x, a, b) служит для расчета значения функции плотности вероятности гамма распределения для параметров распределения a, b и значения случайной величины x. Размерность векторов или матриц x, a и b должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов. Параметры a и b должны быть положительными. Значение случайной величины x должно находиться в интервале ![]() .
.
Функция плотности вероятности гамма распределения имеет вид
![]() ,
,
где ![]() - Гамма – функция.
- Гамма – функция.
Гамма распределение используется в теории надежности для вероятностного описания времени безотказной работы устройств и технических объектов. Гамма распределение, в отличии от экспоненциального распределения, более адекватно описывает надежность работы объекта в следующий момент времени, зависящий от текущего момента на оси времени. Следует отметить, что экспоненциальное и ![]() распределения являются частными случаями гамма распределения.
распределения являются частными случаями гамма распределения.
Примеры:
Использование скалярных аргументов x=0.5; a=1; b=2.
>> x=0.5
x =
0.5000
>> a=1
a =
1
>> b=2
b =
2
>> f = gampdf(x,a,b)
f =
0.3894
Использование векторного аргумента x=[0 0,3 0,6 0, 9]; и скалярных параметров a=1; b=2.
>> x=0:0.3:1
x =
0 0.3000 0.6000 0.9000
>> a=1
a =
1
>> b=2
b =
2
>> f = gampdf(x,a,b)
f =
0.5000 0.4304 0.3704 0.3188
Использование матричных аргумента x, параметра a и скалярного параметра b.
Определение матрицы x.
>> x=0:0.1:1
x =
Columns 1 through 6
0 0.1000 0.2000 0.3000 0.4000 0.5000
Columns 7 through 11
0.6000 0.7000 0.8000 0.9000 1.0000
>> x=[x' x' x' x' x']
x =
0 0 0 0 0
0.1000 0.1000 0.1000 0.1000 0.1000
0.2000 0.2000 0.2000 0.2000 0.2000
0.3000 0.3000 0.3000 0.3000 0.3000
0.4000 0.4000 0.4000 0.4000 0.4000
0.5000 0.5000 0.5000 0.5000 0.5000
0.6000 0.6000 0.6000 0.6000 0.6000
0.7000 0.7000 0.7000 0.7000 0.7000
0.8000 0.8000 0.8000 0.8000 0.8000
0.9000 0.9000 0.9000 0.9000 0.9000
1.0000 1.0000 1.0000 1.0000 1.0000
Определение матрицы a.
>> a=ones(1,11)'
a =
1
1
1
1
1
1
1
1
1
1
1
>> a=[a*2 a*4 a*6 a*8 a*10]
a =
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
Задание скаляра b.
>> b=5
b =
5
Расчет матрицы функции плотности вероятности гамма распределения f.
>> f = gampdf(x,a,b)
f =
0 0 0 0 0
0.0039 0.0000 0.0000 0.0000 0.0000
0.0077 0.0000 0.0000 0.0000 0.0000
0.0113 0.0000 0.0000 0.0000 0.0000
0.0148 0.0000 0.0000 0.0000 0.0000
0.0181 0.0000 0.0000 0.0000 0.0000
0.0213 0.0001 0.0000 0.0000 0.0000
0.0243 0.0001 0.0000 0.0000 0.0000
0.0273 0.0001 0.0000 0.0000 0.0000
0.0301 0.0002 0.0000 0.0000 0.0000
0.0327 0.0002 0.0000 0.0000 0.0000
Рассмотрим изменение вида функции плотности вероятности гамма распределения в зависимости от значения параметров a и b.
Сформируем матрицу x.
>> x=0:0.01:10;
>> x=[x' x' x' x' x'];
Сформируем матрицу a. Значения параметра a будут меняться в последовательности 2, 4, 6, 8, 10.
>> a=ones(1,1001)';
>> a=[a*2 a*4 a*6 a*8 a*10];
Рассмотрим вид функции плотности вероятности гамма распределения для заданной последовательности a и значения параметра b=2.
>> b=2;
>> f = gampdf(x,a,b);
>> plot(x,f)
>> grid on
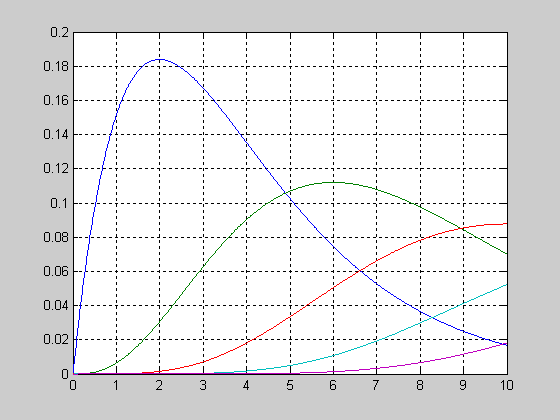
Вид функции плотности вероятности гамма распределения для заданной последовательности a и значения параметра b=8.
>> b=8;
>> x=0:0.01:50;
>> x=[x' x' x' x' x'];
>> a=ones(1,5001)';
>> a=[a*2 a*4 a*6 a*8 a*10];
>> f = gampdf(x,a,b);
>> plot(x,f)
>> grid on
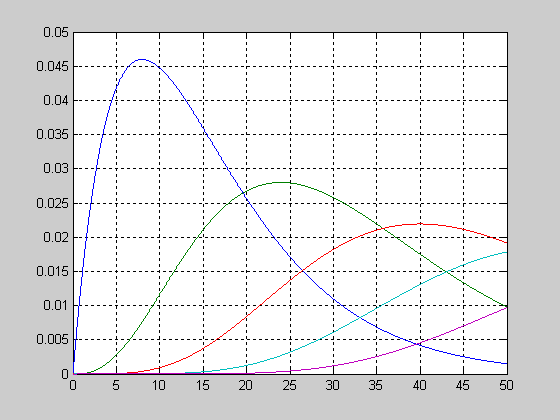
Расчет вероятности попадания случайной величины x в интервал [xmin xmax]. % Расчет ведется по формуле .gif) .
.
Определим пределы интегрирования.
>> xmin=1;
>> xmax=20;
Параметры гамма распределения.
>> a=5;
>> b=8;
Расчет вероятности P попадания x в интервал [xmin xmax].
>> P=quad('gampdf',xmin,xmax,1.e-6,0,a,b)
P =
0.1088
geopdf - Функция плотности вероятности геометрического распределения
Синтаксис:
f = geopdf(x, p)
Описание:
f = geopdf(x, p) - расчета значения функции плотности вероятности геометрического распределения для вероятности появления события в одном опыте p и значения случайной величины x. Размерность векторов или матриц p и x должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение вероятности появления события p находится в интервале [0 1]. Случайная величина x является положительным целым случайным числом.
Функция плотности вероятности геометрического распределения имеет вид
![]() ,
,
где q – вероятность обратного события, q=1-p.
Примеры:
Использование скалярных аргументов x=0.5; p=0.5.
>> x=2
x =
2
>> p=0.5
p =
0.5000
>> f = geopdf(x, p)
f =
0.1250
Использование векторного аргумента x=[0 1 2 3]; и скалярного параметра p=0.5.
>> x=[0 1 2 3]
x =
0 1 2 3
>> p=0.5
p =
0.5000
>> f = geopdf(x, p)
f =
0.5000 0.2500 0.1250 0.0625
Ряд распределения случайной величины при p=0.5 и x=[0 1 2 3 4 5 6 7 8 9].
>> p=0.5;
>> x=[0 1 2 3 4 5 6 7 8 9];
>> f = geopdf(x, p);
>> [x’ f’]
ans =
0 0.5000
1.0000 0.2500
2.0000 0.1250
3.0000 0.0625
4.0000 0.0313
5.0000 0.0156
6.0000 0.0078
7.0000 0.0039
8.0000 0.0020
9.0000 0.0010
Значения функции распределения случайной величины рассчитываются по формуле ![]() ,
, ![]() - k-е значение случайной величины из ряда распределения. Для вероятности появления события p в одном опыте p=0.5 и числе опытов x=[0 1 2 3 4 5 6 7 8 9]:
- k-е значение случайной величины из ряда распределения. Для вероятности появления события p в одном опыте p=0.5 и числе опытов x=[0 1 2 3 4 5 6 7 8 9]:
>> p=0.5;
>> x=[0 1 2 3 4 5 6 7 8 9];
>> f = geopdf(x, p);
>> F = cumsum(f);
>> [x’ F’]
ans =
0 0.5000
1.0000 0.7500
2.0000 0.8750
3.0000 0.9375
4.0000 0.9688
5.0000 0.9844
6.0000 0.9922
7.0000 0.9961
8.0000 0.9980
9.0000 0.9990
График зависимости функции распределения случайной величины
>> bar (x, F, 1)
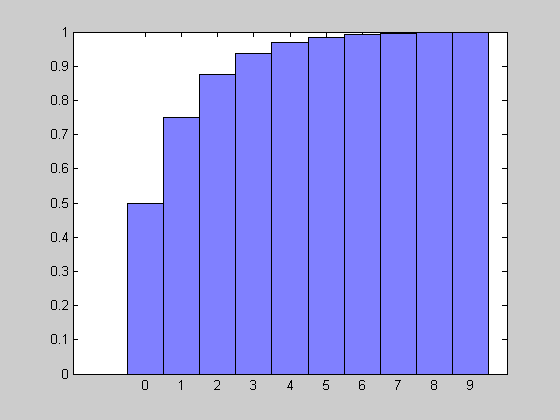
hygepdf - Функция плотности вероятности гипергеометрического распределения
Синтаксис:
f = hygepdf(X,M,K,N)
Описание:
f = hygepdf(X,M,K,N) служит для расчета значений функции плотности вероятности гипергеометрического распределения для параметров распределения M, K, N и значения случайной величины X. Размерность векторов или матриц X, M, K, N должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных аргументов. Величины M, K, N, Х должны быть положительными целыми числами. Значения параметров M, N, K, Х должны удовлетворять следующим неравенствам: M≥N, M≥K, N≥ Х.
Функция плотности вероятности гипергеометрического распределения имеет вид
![]() ,
,
где ![]() - количество вариантов выбора Х объектов из К,
- количество вариантов выбора Х объектов из К, ![]() ; аналогично определяются величины
; аналогично определяются величины ![]() и
и ![]() .
.
Примеры:
Использование скалярных аргументов X=2; K=3; M=5; N=10.
>> N=100
N =
100
>> M=500
M =
500
>> K=30
K =
30
>> X=2
X =
2
>> hygepdf(X,M,K,N)
ans =
0.0308
Ряд распределения случайной величины Х=[0 1 2 3 4 5 6 7 8 9] при M=500, N=100, K=50.
>> M=500
M =
500
>> N=100
N =
100
>> K=50
K =
50
>> X=[0 1 2 3 4 5 6 7 8 9]
X =
0 1 2 3 4 5 6 7 8 9
>> f = hygepdf(X,M,K,N)
>> [X' f']
ans =
0 0.0000
1.0000 0.0001
2.0000 0.0007
3.0000 0.0032
4.0000 0.0103
5.0000 0.0257
6.0000 0.0515
7.0000 0.0852
8.0000 0.1189
9.0000 0.1422
Функция распределения случайной величины Х=[0 1 2 3 4 5 6 7 8 9] при M=500, N=100, K=50.
>> M=500;
>> N=100;
>> K=50;
>> X=[0 1 2 3 4 5 6 7 8 9];
>> f = hygepdf(X,M,K,N);
>> F = cumsum(f);
>> [x’ F’]
ans =
0 0.0000
1.0000 0.0001
2.0000 0.0008
3.0000 0.0040
4.0000 0.0144
5.0000 0.0401
6.0000 0.0915
7.0000 0.1767
8.0000 0.2956
9.0000 0.4378
График зависимости функции распределения случайной величины.
>> bar (x, F, 1)
Рассмотрим решение задачи статистического выборочного контроля качества. В партии из M=10000 шт. изделий находятся N=100 бракованных изделий. Для контроля производится выборка из 50 изделий. Партия считается принятой, если при контроле будет обнаружено не более 2 бракованных изделий. Какова вероятность забраковать партию?
>> M=10000
M =
10000
>> N=100
N =
100
>> K=50
K =
50
Партию забракуют, если будет обнаружено 3 и более несоответствующих изделий. Вероятность забраковать партию Р рассчитаем через обратное событие Q, P=1-Q.
>> X=0:1:2;
>> f = hygepdf(X,M,K,N);
>> X=0:1:2;
>> f = hygepdf(X,M,K,N)
f =
0.6043 0.3067 0.0755
>> Q = sum(f)
Q =
0.9865
>> P=1-Q
P =
0.0135
lognpdf - Функция плотности вероятности логнормального распределения
Синтаксис:
f = lognpdf(x,mu,sigma)
Описание:
f = lognpdf(x,mu,sigma) позволяет рассчитать значение функции плотности вероятности логнормального распределения для параметров распределения mu, sigma и значения случайной величины х. Размерность векторов или матриц x, mu, sigma должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов.
Функция плотности вероятности логнормального распределения имеет вид
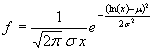 .
.
Примеры:
Использование скалярных аргументов x=0.5; mu=1; sigma=2.
>> x=0.5
x =
0.5000
>> mu=1
mu =
1
>> sigma=2
sigma =
2
>> f = lognpdf(x,mu,sigma)
f =
0.2788
Использование векторного аргумента x=[0 0,3 0,6 0,9]; и скалярных параметров mu=1; sigma=2.
>> x=[0 0.3 0.6 0.9]
x =
0 0.3000 0.6000 0.9000
>> mu=1
mu =
1
>> sigma=2
sigma =
2
>> f = lognpdf(x,mu,sigma)
f =
0 0.3623 0.2499 0.1902
Использование матричных аргумента x, параметра mu и скалярного параметра sigma.
Определение матрицы x.
>> x=0:1:10
x =
0 1 2 3 4 5 6 7 8 9 10
>> x=[x' x' x' x' x']
x =
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
6 6 6 6 6
7 7 7 7 7
8 8 8 8 8
9 9 9 9 9
10 10 10 10 10
Определение матрицы mu.
>> mu=ones(1,11)'
mu =
1
1
1
1
1
1
1
1
1
1
1
>> mu=[mu*2 mu*4 mu*6 mu*8 mu*10]
mu =
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
2 4 6 8 10
Задание скаляра sigma.
>> sigma=4
sigma =
4
Расчет матрицы функции плотности вероятности логнормального распределения.
>> f = lognpdf(x,mu,sigma)
f =
0 0 0 0 0
0.0880 0.0605 0.0324 0.0135 0.0044
0.0473 0.0354 0.0207 0.0094 0.0033
0.0324 0.0256 0.0157 0.0075 0.0028
0.0246 0.0201 0.0128 0.0064 0.0025
0.0199 0.0167 0.0109 0.0056 0.0022
0.0166 0.0143 0.0096 0.0050 0.0020
0.0142 0.0125 0.0085 0.0045 0.0019
0.0125 0.0111 0.0077 0.0042 0.0018
0.0111 0.0100 0.0071 0.0039 0.0017
0.0099 0.0091 0.0065 0.0036 0.0016
Рассмотрим вид функции плотности вероятности логнормального распределения в зависимости от значения параметра mu при постоянном sigma=1.
>> x=0.05:0.01:10;
>> sigma=1;
>> mu=0;
>> f1 = lognpdf(x,mu,sigma);
>> mu=1;
>> f2 = lognpdf(x,mu,sigma);
>> mu=2;
>> f3 = lognpdf(x,mu,sigma);
>> plot(x,f1,x,f2,x,f3)
>> grid on
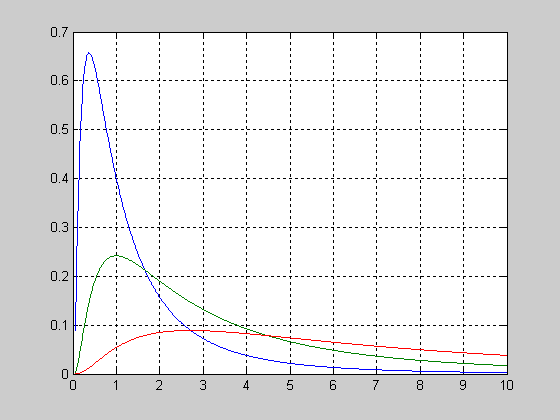
Рассмотрим вид функции плотности вероятности логнормального распределения в зависимости от значения параметра sigma при постоянном mu=0.
>> x=0.05:0.01:4;
>> mu=0;
>> sigma=1;
>> f1 = lognpdf(x,mu,sigma);
>> sigma=2;
>> f2 = lognpdf(x,mu,sigma);
>> sigma=3;
>> f3 = lognpdf(x,mu,sigma);
>> plot(x,f1,':',x,f2,'.',x,f3)
>> grid on
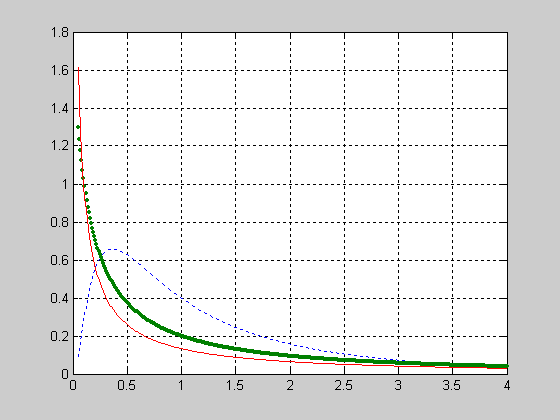
nbinpdf - Функция плотности отрицательного биномиального распределения
Синтаксис:
f = nbinpdf(X,R,P)
Описание:
f = nbinpdf(X,R,P) возвращает значение функции плотности вероятности отрицательного биномиального распределения для случайной величины Х, параметра R и вероятности появления события в одном опыте p. Размерность векторов или матриц X, R, P должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Для нецелых значений случайной величины Х функция плотности отрицательного биномиального распределения равна 0.
Функция плотности отрицательного биномиального распределения имеет вид
![]() ,
,
где ![]() - число сочетаний, которым можно выбрать Х объектов из R+X-1,
- число сочетаний, которым можно выбрать Х объектов из R+X-1, ![]() , q – вероятность обратного события, q=1-p.
, q – вероятность обратного события, q=1-p.
Простейшим случаем применения функции плотности отрицательного биномиального распределения является расчет вероятности появления некоторого события при независимых испытаниях с постоянной вероятностью появления события в одном опыте Р. Число дополнительных испытаний которое должно быть проведено, чтобы получить заданное число R успешных попыток имеет отрицательное биномиальное распределение. Однако более общая трактовка отрицательного биномиального распределения позволяет задавать параметр R как положительное вещественное число. Для вещественного R коэффициент биномиального распределения рассчитывается как ![]() , где
, где ![]() - Гамма-функция.
- Гамма-функция.
Примеры:
Использование скалярных аргументов X=2, R=10, P=0.5
>> X=2
X =
2
>> R=10
R =
10
>> P=0.5
P =
0.5000
>> f = nbinpdf(X,R,P)
f =
0.0134
Расчет ряда распределения для случайной величины X=[0 1 2 3 4 5 6 7 8 9] и аргументов R=10, P=0.5
>> X=0:1:20;
>> R=10;
>> P=0.5;
>> f = nbinpdf(X,R,P);
>> [X' f']
ans =
0 0.0010
1.0000 0.0049
2.0000 0.0134
3.0000 0.0269
4.0000 0.0436
5.0000 0.0611
6.0000 0.0764
7.0000 0.0873
8.0000 0.0927
9.0000 0.0927
10.0000 0.0881
11.0000 0.0801
12.0000 0.0701
13.0000 0.0593
14.0000 0.0487
15.0000 0.0390
16.0000 0.0304
17.0000 0.0233
18.0000 0.0175
19.0000 0.0129
20.0000 0.0093
Графическое представление ряда распределения
>> plot(X,f,'+')
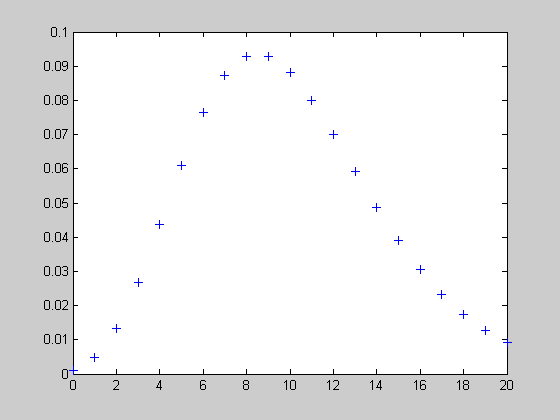
ncfpdf - Функция плотности вероятности смещенного распределения Фишера (смещенного F распределения)
Синтаксис:
f = ncfpdf(X,NU1,NU2,DELTA)
Описание:
f = ncfpdf(X,NU1,NU2,DELTA) служит для расчета значений функции плотности вероятности смещенного распределения Фишера для значений случайной величины Х, степеней свободы NU1, NU2 и положительного параметра смещения DELTA. Размерность векторов или матриц X, NU1 ,NU2 ,DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Распределение Фишера является частным случаем смещенного распределения Фишера с параметром DELTA равным 0. Увеличение параметра смещения DELTA приводит к смещению распределения в правую сторону с увеличением величины рассеяния (см. пример).
Примеры:
Использование скалярных аргументов X=0.1; NU1=5; NU2=8; DELTA=1.
>> X=0.1
X =
0.1000
>> NU1=5
NU1 =
5
>> NU2=8
NU2 =
8
>> DELTA=1
DELTA =
1
>> f = ncfpdf(X,NU1,NU2,DELTA)
f =
0.1555
Использование векторной случайной величины X=0:0.1:1 и скалярных аргументов NU1=5; NU2=8; DELTA=1.
>> X=0:0.1:1;
>> NU1=5;
>> NU2=8;
>> DELTA=1;
>> f = ncfpdf(X,NU1,NU2,DELTA);
>> [X' f']
ans =
0 0
0.1000 0.1555
0.2000 0.3243
0.3000 0.4448
0.4000 0.5172
0.5000 0.5518
0.6000 0.5595
0.7000 0.5490
0.8000 0.5269
0.9000 0.4980
1.0000 0.4656
Исследование влияния коэффициента смещения DELTA=[0 1 2] на вид функции плотности вероятности смещенного распределения Фишера
>> X=0:0.1:5;
>> NU1=5;
>> NU2=8;
>> DELTA=0;
>> f1 = ncfpdf(X,NU1,NU2,DELTA);
>> DELTA=1;
>> f2 = ncfpdf(X,NU1,NU2,DELTA);
>> DELTA=2;
>> f3 = ncfpdf(X,NU1,NU2,DELTA);
>> plot(X,f1,X,f2,'.',X,f3,'+')
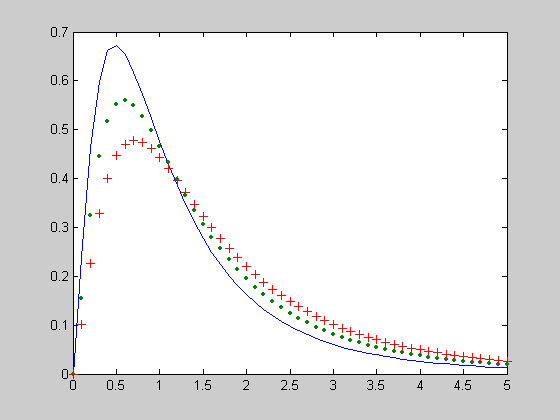
nctpdf - Функция плотности вероятности смещенного распределения Стьюдента (смещенного T распределения)
Синтаксис:
f = nctpdf(X,V,DELTA)
Описание:
f = nctpdf(X,V,DELTA) служит для расчета значений функции плотности вероятности смещенного распределения Стьюдента для значений случайной величины Х, степени свободы V и параметра смещения DELTA. Размерность векторов или матриц X, NU1, NU2, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Примеры:
Использование скалярных аргументов X=0.1; V=5; DELTA=1.
>> X=0.1
X =
0.1000
>> V=5
V =
5
>> DELTA=1
DELTA =
1
>> f = nctpdf(X,V,DELTA)
f =
0.2543
Использование векторной случайной величины X=0:0.1:1 и скалярных аргументов V=10; DELTA=1.
>> X=0:0.1:1;
>> V=10;
>> DELTA=1;
>> f = nctpdf(X,V,DELTA);
>> [X' f']
ans =
0 0.2360
0.1000 0.2601
0.2000 0.2836
0.3000 0.3058
0.4000 0.3261
0.5000 0.3439
0.6000 0.3586
0.7000 0.3698
0.8000 0.3772
0.9000 0.3805
1.0000 0.3798
Исследование влияния коэффициента смещения DELTA=[0 1 2] на вид функции плотности вероятности смещенного распределения Стьюдента
>> X=-5:0.1:5;
>> V=5;
>> DELTA=0;
>> f1 = nctpdf(X,V,DELTA);
>> DELTA=1;
>> f2 = nctpdf(X,V,DELTA);
>> DELTA=2;
>> f3 = nctpdf(X,V,DELTA);
>> plot(X,f1,X,f2,'.',X,f3,'+')
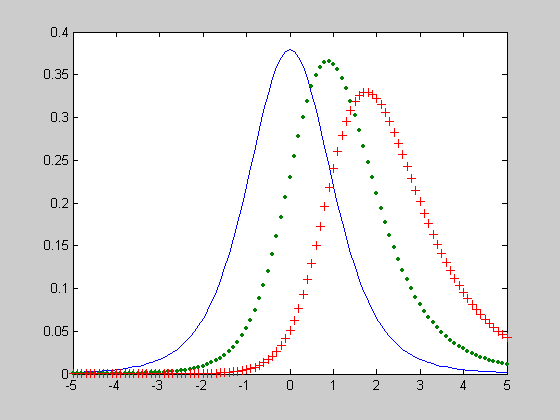
ncx2pdf - Функция плотности вероятности смещенного распределения хи-квадрат
Синтаксис:
f = ncx2pdf(X,V,DELTA)
Описание:
f = ncx2pdf(X,V,DELTA) служит для расчета значений функции плотности вероятности смещенного распределения хи-квадрат для значений случайной величины Х, степени свободы V и параметра смещения DELTA. Размерность векторов или матриц X, V, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
Примеры:
Использование скалярных аргументов X=0.1; V=5; DELTA=1.
>> X=0.1
X =
0.1000
>> V=5
V =
5
>> DELTA=1
DELTA =
1
>> f = ncx2pdf(X,V,DELTA)
f =
0.0025
Использование векторной случайной величины X=0:0.1:1 и скалярных аргументов V=10; DELTA=1.
>> X=0:0.1:1;
>> V=10;
>> DELTA=1;
>> f = ncx2pdf(X,V,DELTA);
>> [X' f']
ans =
0 0
0.1000 0.0000
0.2000 0.0000
0.3000 0.0000
0.4000 0.0000
0.5000 0.0000
0.6000 0.0001
0.7000 0.0001
0.8000 0.0002
0.9000 0.0003
1.0000 0.0005
Исследование влияния коэффициента смещения DELTA=[0 1 2 3] на вид функции плотности вероятности смещенного распределения хи-квадрат
>> X=0:0.1:5;
>> V=5;
>> DELTA=0;
>> f1 = ncx2pdf(X,V,DELTA);
>> DELTA=1;
>> f2= ncx2pdf(X,V,DELTA);
>> DELTA=2;
>> f3=ncx2pdf(X,V,DELTA);
>> plot(X,f1,X,f2,'.',X,f3,'+')
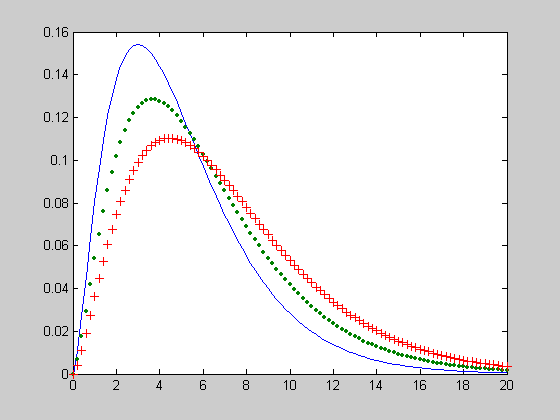
normpdf - Функция плотности вероятности нормального распределения
Синтаксис:
f = normpdf(X,MU,SIGMA)
Описание:
f = normpdf(X,MU,SIGMA) служит для расчета значений функции плотности вероятности нормального распределения для значений случайной величины Х, математического ожидания MU и среднего квадратического отклонения SIGMA. Размерность векторов или матриц X, MU, SIGMA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение среднего квадратического отклонения SIGMA должно быть положительным.
Функция плотности нормального распределения имеет вид
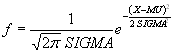 .
.
Стандартное нормальное распределение имеет параметры распределения равные MU=0 и SIGMA=1. Функция плотности стандартного нормального распределения имеет вид ![]() . Если случайная величина Х является стандартное нормальной случайной величиной, тогда случайная величина
. Если случайная величина Х является стандартное нормальной случайной величиной, тогда случайная величина ![]() распределена по нормальному закону с параметрами MU, SIGMA. Справедливо также и обратное утверждение если случайная величина Х распределена по нормальному закону, то случайная величина
распределена по нормальному закону с параметрами MU, SIGMA. Справедливо также и обратное утверждение если случайная величина Х распределена по нормальному закону, то случайная величина ![]() распределена по стандартному нормальному закону.
распределена по стандартному нормальному закону.
Примеры:
Использование скалярных аргументов X=0.1; MU=0; SIGMA=1.
>> X=0.1
X =
0.1000
>> MU=0
MU =
0
>> SIGMA=1
SIGMA =
1
>> f = normpdf(X,MU,SIGMA)
f =
0.3970
Использование векторной случайной величины X=0:0.1:1 и скалярных параметров распределения MU =0; SIGMA =1.
>> X=0:0.1:1;
>> MU =0;
>> SIGMA =1;
>> f = normpdf(X,MU,SIGMA);
>> [X' f']
ans =
0 0.3989
0.1000 0.3970
0.2000 0.3910
0.3000 0.3814
0.4000 0.3683
0.5000 0.3521
0.6000 0.3332
0.7000 0.3123
0.8000 0.2897
0.9000 0.2661
1.0000 0.2420
Исследование влияния дисперсии D=[0 4 9] на вид функции плотности вероятности нормального распределения при нулевом математическом ожидании.
>> X=-9:0.2:9;
>> MU=0;
>> SIGMA=sqrt(1);
>> f1 = normpdf(X,MU,SIGMA);
>> SIGMA=sqrt(4);
>> f2 = normpdf(X,MU,SIGMA);
>> SIGMA=sqrt(9);
>> f3 = normpdf(X,MU,SIGMA);
>> plot(X,f1,X,f2,'.',X,f3,'+')
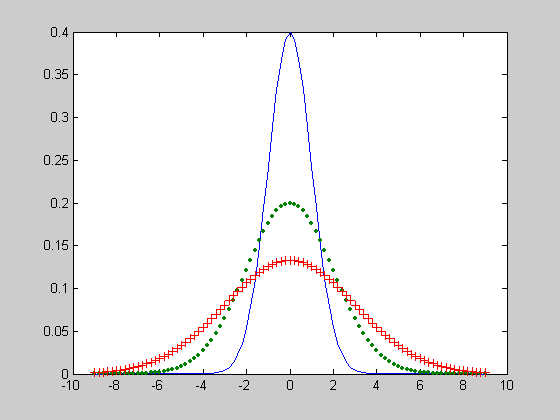
poisspdf - Функция плотности вероятности распределения Пуассона
Синтаксис:
f = poisspdf(X,LAMBDA)
Описание:
f=poisspdf(X,LAMBDA) возвращает значение функции плотности вероятности распределения Пуассона для случайной величины Х и параметра LAMBDA. Размерность векторов или матриц X, LAMBDA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение параметра LAMBDA должно быть положительным.
Функция плотности вероятности распределения Пуассона имеет вид
![]() ,
,
где Х может принимать целые неотрицательные значения. Функция плотности вероятности распределения Пуассона равна нулю если Х не является целым числом.
Примеры:
Использование скалярных аргументов X=2; LAMBDA=1.
>> X=2
X =
2
>> LAMBDA=1
LAMBDA =
1
>> f = poisspdf(X,LAMBDA)
f =
0.1839
Использование векторной случайной величины X=0:1:10 и скалярного аргумента LAMBDA=2.
>> X=0:1:10;
>> LAMBDA=2;
>> f = poisspdf(X,LAMBDA);
>> [X' f']
ans =
0 0.1353
1.0000 0.2707
2.0000 0.2707
3.0000 0.1804
4.0000 0.0902
5.0000 0.0361
6.0000 0.0120
7.0000 0.0034
8.0000 0.0009
9.0000 0.0002
10.0000 0.0000
Исследование влияния параметра LAMBDA=[1 2 4] на вид функции плотности вероятности смещенного распределения Пуассона
>> X=0:1:10;
>> LAMBDA=1;
>> f1 = poisspdf(X,LAMBDA);
>> LAMBDA=2;
>> f2 = poisspdf(X,LAMBDA);
>> LAMBDA=4;
>> f3 = poisspdf(X,LAMBDA);
>> plot(X,f1,'o',X,f2,'.',X,f3,'+')
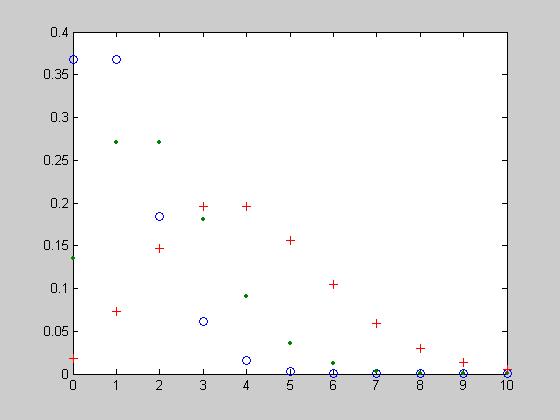
Рассмотрим решение задачи. При производстве жестких дисков для винчестеров наблюдается в среднем 2 повреждения на 4ГБ дискового пространства. Такой уровень дефектности является приемлемым. Определить какова вероятность что жесткий диск не имеет дефектов.
Х – количество дефектов.
>> X=0
X =
0
LAMBDA – среднее число дефектов на 4ГБ дисковой памяти.
>> LAMBDA=2
LAMBDA =
2
>> p = poisspdf(X, LAMBDA)
p =
0.1353
mvnpdf - Функция плотности вероятности многомерного нормального распределения
Синтаксис:
f = mvnpdf(X)
f = mvnpdf(X,MU)
f = mvnpdf(X,MU,SIGMA)
Описание:
f = mvnpdf(X) возвращает матрицу f с размерностью n-1, содержащий значения функции плотности вероятности многомерного нормального распределения c нулевым средним и ковариационной матрицей, рассчитанной для каждого ряда матрицы Х с размерностью n–d. Ряды матрицы Х соответствуют наблюдениям, и столбцы – случайным переменным.
f = mvnpdf(X,MU) – возвращает значения функции плотности вероятности многомерного нормального распределения со средним MU и ковариационной матрицей, рассчитанной для каждого ряда матрицы Х. MU является матрицей с размерностью 1–d или n – d. Если MU является матрицей, функция плотности вероятности многомерного нормального распределения рассчитывается для каждого ряда матрицы Х с соответствующим значением матрицы MU. Если MU скалярное значение, то размерность MU увеличивается до размерности Х, а значения элементов матрицы принимаются равными скалярному аргументу.
f = mvnpdf(X,MU,SIGMA) возвращает значения функции плотности вероятности многомерного нормального распределения со средним MU и ковариационным моментом SIGMA, рассчитанные для каждого ряда матрицы Х. SIGMA является матрицей с размерностью d-d или массивом с размерностью d–d–n. В последнем случае функция плотности вероятности рассчитывается для каждого ряда Х с соответствующим третьим измерением массива SIGMA, так как mvnpdf вычисляет значение f(i) на основе X (i,:) и SIGMA (:,:,i). Если необходимо установить значение параметра MU по умолчанию при заданном массиве SIGMA используется операция [ ].
Если Х задан как вектор 1–d, его размерность увеличивается до максимальной размерности MU или до совпадения с размерностью SIGMA.
Функция плотности отрицательного многомерного нормального распределения для двух случайных величин ![]() ,
, ![]() имеет вид
имеет вид
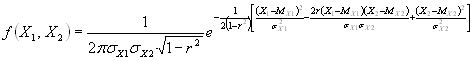 ,
,
где ![]() ,
, ![]() - средние квадратические отклонения
- средние квадратические отклонения ![]() ,
, ![]() ;
; ![]() - коэффициент парной корреляции между
- коэффициент парной корреляции между ![]() ,
, ![]() ;
; ![]() ,
, ![]() - средние арифметические значения
- средние арифметические значения ![]() ,
, ![]() .
.
Функция плотности вероятности многомерного нормального распределения для параметров sigma1=1, sigma2=1, MX1=0, MX2=0, r=0 (рис. 1) и sigma1=1, sigma2=3, MX1=0, MX2=0, r=0 (рис. 1) имеет вид
>> sigma1=1;sigma2=1;MX1=0;MX2=0;r=0;
>> [X1 X2]=meshgrid([-3:0.1:3]);
>> f=1/(2.*pi.*sigma1.*sigma1.*sqrt(1-r.^2)).*exp(-1./(2.*(1-r.^2)).*((X1-MX1).^2./sigma1+(X2-MX2).^2./sigma2-2.*r.*(X1-MX1).^2.*(X2-MX2).^2./sigma1./sigma2));
>> surf(X1,X2,f)
>> sigma1=1;sigma2=3;MX1=0;MX2=0;r=0;
>> [X1 X2]=meshgrid([-3:0.1:3]);
>> f=1/(2.*pi.*sigma1.*sigma1.*sqrt(1-r.^2)).*exp(-1./(2.*(1-r.^2)).*((X1-MX1).^2./sigma1+(X2-MX2).^2./sigma2-2.*r.*(X1-MX1).^2.*(X2-MX2).^2./sigma1./sigma2));
>> surf(X1,X2,f)
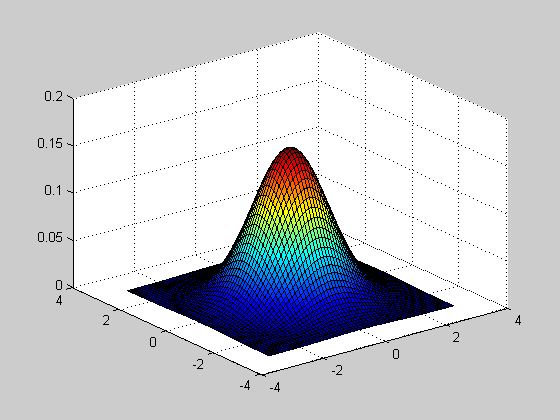
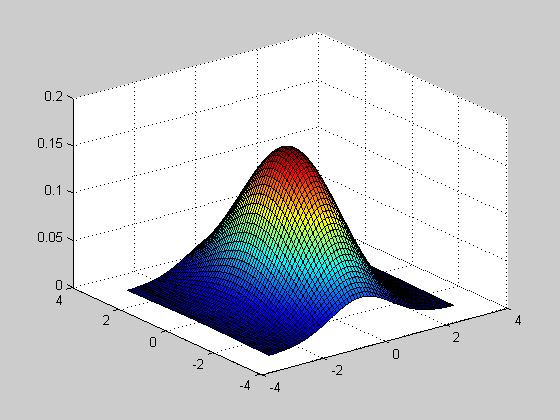
Рис. 1 Рис. 2
Влияние коэффициента корреляции между случайными величинами на функцию плотности вероятности многомерного нормального распределения можно оценить из рис. 3 (r=0) и рис. 4 (r=3).
>> sigma1=1;sigma2=1;MX1=0;MX2=0;r=0;
>> [X1 X2]=meshgrid([-3:0.1:3]);
>> f=1/(2.*pi.*sigma1.*sigma1.*sqrt(1-r.^2)).*exp(-1./(2.*(1-r.^2)).*((X1-MX1).^2./sigma1+(X2-MX2).^2./sigma2-2.*r.*(X1-MX1).^2.*(X2-MX2).^2./sigma1./sigma2));
>> surf(X1,X2,f)
>> sigma1=1;sigma2=1;MX1=0;MX2=0;r=0.1;
>> [X1 X2]=meshgrid([-3:0.1:3]);
>> f=1/(2.*pi.*sigma1.*sigma1.*sqrt(1-r.^2)).*exp(-1./(2.*(1-r.^2)).*((X1-MX1).^2./sigma1+(X2-MX2).^2./sigma2-2.*r.*(X1-MX1).^2.*(X2-MX2).^2./sigma1./sigma2));
>> surf(X1,X2,f)
.gif)
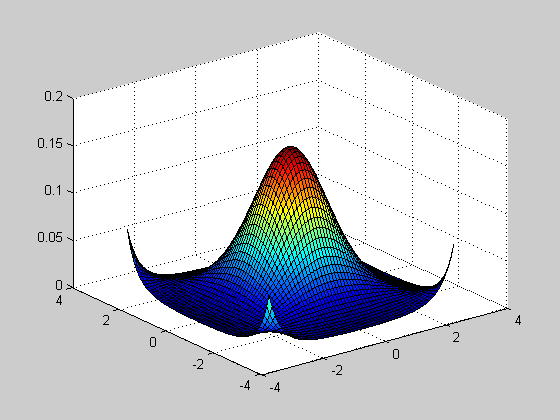
Рис. 3 Рис. 4
Примеры:
>> mu = [1 -1]
mu =
1 -1
>> Sigma = [.9 .4; .4 .3]
Sigma =
0.9000 0.4000
0.4000 0.3000
>> X = mvnrnd(mu,Sigma,10)
X =
0.5896 -1.2477
-0.5801 -1.4485
1.1189 -1.1528
1.2729 -0.1155
-0.0876 -1.5311
2.1298 -0.4580
2.1281 -0.1257
0.9643 -0.9951
1.3105 -0.8954
1.1657 -1.2174
>> p = mvnpdf(X,mu,Sigma)
p =
0.4295
0.0921
0.4005
0.0425
0.2464
0.2346
0.1339
0.4787
0.4528
0.3342
raylpdf - Функция плотности вероятности распределения Релея
Синтаксис:
f = raylpdf(X,B)
Описание:
f = raylpdf(X,B) возвращает значение функции плотности вероятности распределения Релея для случайной величины Х и параметра B. Размерность векторов или матриц X, B должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Функция плотности вероятности распределения Релея имеет вид
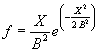 .
.
Примеры:
Использование скалярных аргументов X=2; B=1.
>> X=2
X =
2
>> B=1
B =
1
>> f = raylpdf(X,B)
f =
0.2707
Использование векторной случайной величины X=0:1:5 и скалярного параметра B=1.
>> X=0:1:5
X =
0 1 2 3 4 5
>> B=1
B =
1
>> f = raylpdf(X,B)
f =
0 0.6065 0.2707 0.0333 0.0013 0.0000
Исследование влияния параметра В=[1 2 4] на вид функции плотности вероятности распределения Релея.
>> X=0:0.1:10;
>> B=1;
>> f1 = raylpdf(X,B);
>> B=2;
>> f2 = raylpdf(X,B);
>> B=4;
>> f3 = raylpdf(X,B);
>> plot(X,f1,X,f2,'.',X,f3,'+')
>> grid on
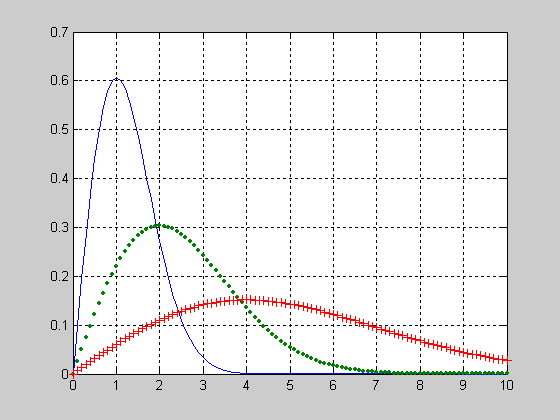
pdf - Параметрическая функция плотности вероятности
Синтаксис:
f = pdf('name',X,A1,A2,A3)
Описание:
f = pdf('name',X,A1,A2,A3) возвращает значение функции плотности вероятности для случайной величины Х и параметров 'name', A1, A2, A3. Строковая переменная 'name' задает вид распределения в соответствии со следующей таблицей
|
Вид распределения |
Переменная 'name' |
|
Бета |
'beta', 'Beta' |
|
Биномиальное |
'bino', 'Binomial' |
|
Хи-квадрат |
'chi2', 'Chisquare' |
|
Экспоненциальное |
'exp', 'Exponential' |
|
Фишера |
'f', 'F' |
|
Гамма |
'gam', 'Gamma' |
|
Геометрическое |
'geo', 'Geometric' |
|
Гипергеометрическое |
'hyge', 'Hypergeometric' |
|
Логнормальное |
'logn', 'Lognormal' |
|
Отрицательное биномиальное |
'nbin', 'Negative Binomial' |
|
Смещенное Фишера |
'ncf', 'Noncentral F' |
|
Смещенное Стьюдента |
'nct', 'Noncentral T' |
|
Смещенное хи-квадрат |
'ncx2', 'Noncentral Chi-square' |
|
Нормальное |
'norm', 'Normal' |
|
Пуассона |
'poiss', 'Poisson' |
|
Релея |
'rayl', 'Rayleigh' |
|
Стьюдента |
't', 'T' |
|
Дискретное равномерное |
'unid', 'Discrete Uniform' |
|
Непрерывное равномерное |
'unif', 'Uniform' |
|
Вейбулла |
'weib', 'Weibull' |
Параметры A1, A2, A3 являются параметрами перечисленных выше распределений. Последовательность и количество передаваемых параметров A1, A2, A3 должны соответствовать числу и последовательности передаваемым параметрам соответствующих функций распределения. Размерность векторов или матриц X, A1, A2, A3 должна быть одинаковой. Размерность параметров должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
Примеры:
Расчет значений функции плотности вероятности нормального распределения в диапазоне значений случайной величины X= -2:2, с математическим ожиданием равным 0 и средним квадратическим отклонением равным 1.
>> p = pdf('Normal',-2:2,0,1)
p =
0.0540 0.2420 0.3989 0.2420 0.0540
График плотности вероятности стандартизованного нормального распределения.
>> p = pdf('Normal',-3:0.01:3,0,1);
>> plot(-3:0.01:3,p)
>> grid on
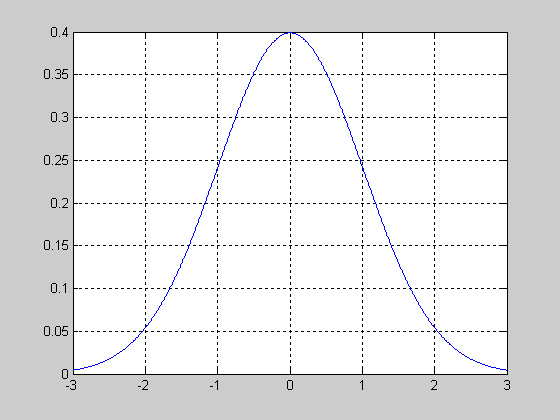
tpdf - Функция плотности вероятности распределения Стьюдента
Синтаксис:
f = tpdf(X,V)
Описание:
f = tpdf(X,V) служит для расчета значений функции плотности вероятности распределения Стьюдента для значений случайной величины Х и степени свободы V. Размерность векторов или матриц X, V должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение числа степеней свободы V должно быть положительным целым числом.
Функция плотности вероятности распределения Стьюдента имеет вид
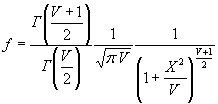 .
.
Примеры:
Использование скалярных аргументов X=2; V=10.
>> X=2
X =
2
>> V=10
V =
10
>> f = tpdf(X,V)
f =
0.0611
Использование векторной случайной величины X=0:1:5 и скалярного параметра V=10.
>> X=0:1:5
X =
0 1 2 3 4 5
>> V=10
V =
10
>> f = tpdf(X,V)
f =
0.3891 0.2304 0.0611 0.0114 0.0020 0.0004
Исследование влияния числа степеней свободы V=[10 20 40] на вид функции плотности вероятности распределения Стьюдента.
>> X=0:0.1:5;
>> V=2;
>> f1 = tpdf(X,V);
>> V=5;
>> f2 = tpdf(X,V);
>> V=50;
>> f3 = tpdf(X,V);
>> plot(X,f1,X,f2,'.',X,f3,'+')
>> grid on
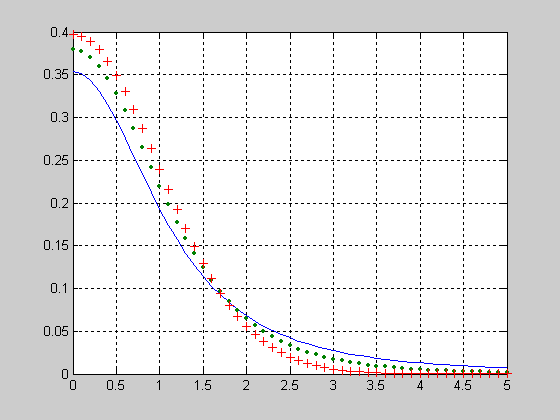
unidpdf - Функция плотности вероятности дискретного равномерного распределения
Синтаксис:
f = unidpdf(X,N)
Описание:
f = unidpdf(X,N) возвращает значение функции плотности вероятности дискретного равномерного распределения для случайной величины Х и параметра N. Размерность векторов или матриц X и N должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого аргумента. Значение параметра N должно быть целым и положительным.
Функция плотности вероятности дискретного равномерного распределения имеет вид
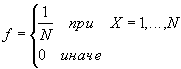 .
.
Величину f можно рассматривать как вероятность появления любого числа из ряда 1,…,N.
Примеры:
Использование скалярных аргументов X=2; N=10.
>> X=2
X =
2
>> N=10
N =
10
>> f = unidpdf(X,N)
f =
0.1000
Использование векторной случайной величины X=0:1:5 и скалярного параметра N=10.
>> X=0:1:5
X =
0 1 2 3 4 5
>> N=10
N =
10
>> f = unidpdf(X,N)
f =
0 0.1000 0.1000 0.1000 0.1000 0.1000
Вид функции плотности вероятности дискретного равномерного распределения для N=10 и N=15
>> X=-2:1:25;
>> N=10;
>> f1 = unidpdf(X,N);
>> N=15;
>> f2 = unidpdf(X,N);
>> plot(X,f1,X,f2)
>> grid on
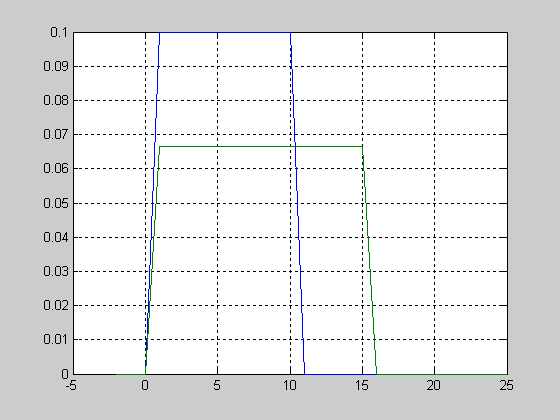
weibpdf - Функция плотности вероятности распределения Вейбулла
Синтаксис:
f = weibpdf(X,A,B)
Описание:
f = weibpdf(X,A,B) возвращает значение функции плотности вероятности распределения Вейбулла для случайной величины Х и параметров A, B. Размерность векторов или матриц X, A, B должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных параметров. Значения величин A и B должны быть положительными.
Функция плотности вероятности распределения Вейбулла имеет вид
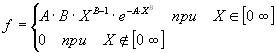 .
.
Примеры:
Использование скалярных аргументов X=0.1; A=1; B=1.
>> X=0.1
X =
0.1000
>> A=1
A =
1
>> B=1
B =
1
>> f = weibpdf(X,A,B)
f =
0.9048
Использование векторной случайной величины X=0:0.1:1 и скалярных параметров распределения A=1; B=1.
>> A=1
A =
1
>> B=1
B =
1
>> X=0:0.1:1
X =
Columns 1 through 8
0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000
Columns 9 through 11
0.8000 0.9000 1.0000
>> f = weibpdf(X,A,B)
f =
Columns 1 through 8
1.0000 0.9048 0.8187 0.7408 0.6703 0.6065 0.5488 0.4966
Columns 9 through 11
0.4493 0.4066 0.3679
Исследование влияния параметра A=[1 2 4] на вид функции плотности вероятности распределения Вейбулла при B=4.
>> B=4;
>> X=0:0.01:2;
>> A=1;
>> f1 = weibpdf(X,A,B);
>> A=2;
>> f2 = weibpdf(X,A,B);
>> A=4;
>> f3 = weibpdf(X,A,B);
>> plot(X,f1,X,f2,'.',X,f3,'+')
>> grid on
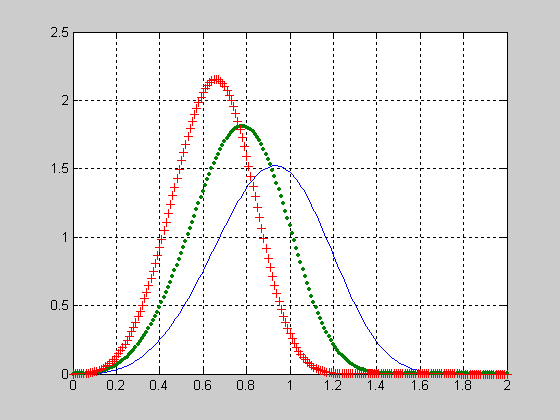
chi2inv - Обратная функция распределения хи-квадрат
Синтаксис:
X = chi2inv(P,V)
Описание:
chi2inv(P,V) служит для расчета значения обратной функции распределения вероятностей ![]() для параметра распределения V и значения вероятности появления значения случайной величины P. Размерность матриц V и P должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Число степеней свободы V должно быть целым положительным числом. Значение вероятности P должно находится в интервале [0 1].
для параметра распределения V и значения вероятности появления значения случайной величины P. Размерность матриц V и P должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Число степеней свободы V должно быть целым положительным числом. Значение вероятности P должно находится в интервале [0 1].
Обратная функция распределения ![]() имеет вид
имеет вид
![]() ,
,
где 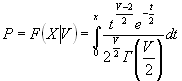 ,
, ![]() - Гамма-функция.
- Гамма-функция.
Результат расчета X – квантиль распределения ![]() соответствующая попаданию случайной величины в интервал (-∞ X] с вероятностью P при заданном числе степеней свободы V.
соответствующая попаданию случайной величины в интервал (-∞ X] с вероятностью P при заданном числе степеней свободы V.
Примеры:
Определить квантиль распределения ![]() с числом степеней свободы V=10 соответствующую 95% попадания значения случайной величины в интервал (-∞ X].
с числом степеней свободы V=10 соответствующую 95% попадания значения случайной величины в интервал (-∞ X].
>> P=0.95;
>> V=10;
>> X = chi2inv(P,V)
X =
18.3070
Вероятность получить значение случайной величины распределенной по закону ![]() с V=10 более 18.3070 составляет 5%.
с V=10 более 18.3070 составляет 5%.
Вид обратной функции распределения вероятностей хи-квадрат при V=5; V=10; V=20.
>> P=0:0.01:1;
>> V=5;
>> X1 = chi2inv(P,V);
>> V=10;
>> X2 = chi2inv(P,V);
>> V=20;
>> X3 = chi2inv(P,V);
>> plot(P,X1,’r’, P,X2,’g’, P,X3,’b’)
>> grid on
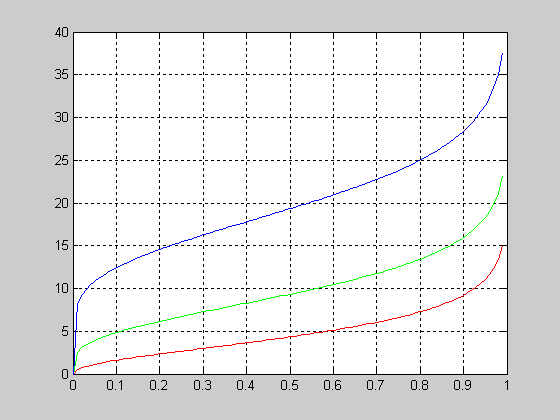
expinv - Обратная функция распределения вероятностей экспоненциального закона
Синтаксис:
X = expinv(P,MU)
Описание:
expinv(P,MU) cлужит для расчета значений квантилей экспоненциального закона для параметра распределения MU (![]() ) и вероятности появления значения случайной величины P. Размерность векторов или матриц P и MU должна быть одинаковой. Размерность скалярного параметра увеличивается до размера другого входного аргумента. Параметр MU должен быть положительным числом. Значение вероятности P должно находиться в интервале [0 1].
) и вероятности появления значения случайной величины P. Размерность векторов или матриц P и MU должна быть одинаковой. Размерность скалярного параметра увеличивается до размера другого входного аргумента. Параметр MU должен быть положительным числом. Значение вероятности P должно находиться в интервале [0 1].
Вид обратной функции распределения вероятностей экспоненциального закона
![]() .
.
Результат расчета X – квантиль распределения экспоненциального закона, соответствующая попаданию случайной величины в интервал (-∞ X] с вероятностью P при заданной величине параметра MU.
Примеры:
Рассмотрим решение следующей задачи. Допустим, что время безотказной работы электрических ламп распределено по экспоненциальному закону с параметром µ = 700 часов. Определить среднее время безотказной работы ламп.
Зададим вероятность выхода из строя ламп на уровне 50%.
>> P=0.5;
Количество часов соответствующее 50% времени безотказной работы определяется как квантиль экспоненциального закона
>> MU=700;
>> expinv(P, MU)
ans =
485.2030
Полученный результат означает, что из комплекта электрических ламп с 700 часовым средним временем жизни половина выйдет из строя менее чем через 500 часов эксплуатации.
Оценить зависимость времени безотказной работы лампы от среднего времени жизни µ и вероятности отказа P.
>> P=0:0.01:1;
>> MU=500;
>> X1=expinv(P, MU);
>> MU=1000;
>> X2=expinv(P, MU);
>> MU=1500;
>> X3=expinv(P, MU);
>> plot(P,X1,’r’, P,X2,’g’, P,X3,’b’)
>> grid on
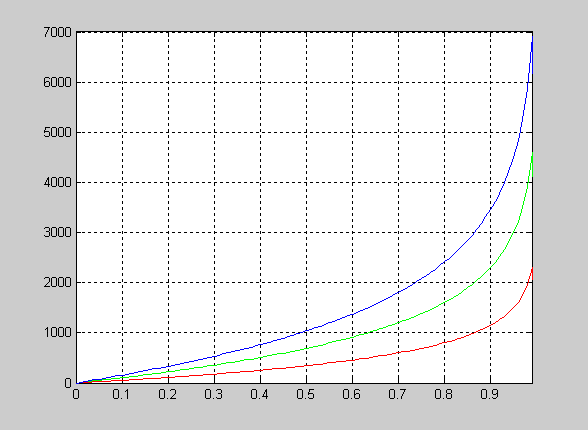
finv - Обратная функция распределения вероятностей закона Фишера
Синтаксис:
X = finv(P,V1,V2)
Описание:
finv(P,V1,V2) служит для расчета значения квантили закона Фишера для параметров распределения V1, V2 и значения вероятности P. Размерность векторов или матриц P, V1 и V2 должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов. Параметры V1 и V2 должны быть положительными целыми числами. Значение вероятности P должно находиться в интервале [0 1].
Обратная функция распределения Фишера имеет вид
![]() ,
,
где 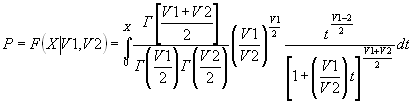 ,
, ![]() - Гамма-функция.
- Гамма-функция.
Результат расчета X – квантиль распределения закона Фишера, соответствующая попаданию случайной величины в интервал (-∞ X] с вероятностью P при заданных значениях чисел степеней свободы V1, V2.
Примеры:
Определить значение квантили распределения Фишера со степенями свободы V1=5, V2=10 соответствующей 95% доверительной вероятности.
Определение параметров распределения
>> V1=5;
>> V2=10;
Определение доверительной вероятности
>> P=0.95;
>> X = finv(P,V1,V2)
X =
3.3258
Полученный результат показывает, что только 5% значений случайной величины попадут в интервал (3.3258 +∞).
Зависимость квантили закона Фишера от вероятности P и чисел степеней свободы V1=5, V2=10.
>> [V1 P] = meshgrid([0:1:20], [0:0.05:1]);
>> V2=10;
>> X = finv(P,V1,V2);
>> subplot(2,1,1)
>> surf(V1,P,X)
>> [V2 P] = meshgrid([10:1:20], [0:0.05:1]);
>> V1=10;
>> X = finv(P,V1,V2);
>> subplot(2,1,2)
>> surf(V2,P,X)
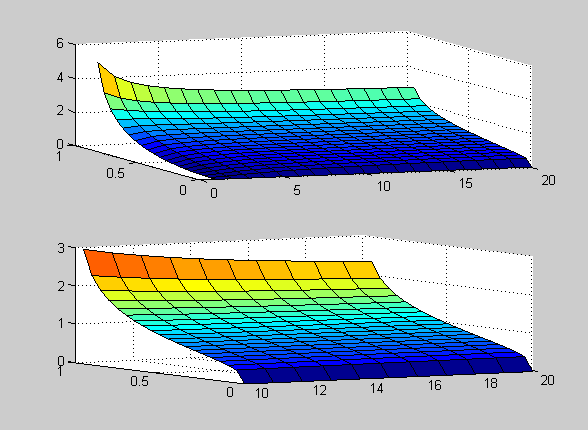
gaminv - Обратная функция вероятностей гамма распределения
Синтаксис:
X = gaminv(P,A,B)
Описание:
gaminv(P,A,B) позволяет рассчитать значения квантили гамма распределения с параметрами A, B и значением вероятности Р. Размерность векторов или матриц Р, A и B должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов. Параметры A и B должны быть положительными. Значение вероятности Р должно быть в интервале [0 1].
Обратная функция вероятностей гамма распределения имеет вид
![]()
где 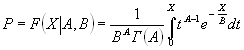 ,
, ![]() - Гамма – функция.
- Гамма – функция.
Поскольку не существует аналитического решения приведенного интегрального уравнения, для расчета значения квантили гамма распределения используется итеративная процедура поиска на основе метода Ньютона.
Примеры:
Использование скалярных аргументов P=0.5; A=1; B=2.
>> P=0.5
P =
0.5000
>> A=1
A =
1
>> B=2
B =
2
>> X = gaminv(P,A,B)
X =
1.3863
Использование векторного аргумента P=[0.1 0.3 0.6 0.9]; и скалярных параметров A=1; B=2.
>> P=[0.1 0.3 0.6 0.9]
P =
0.1000 0.3000 0.6000 0.9000
>> A=1
A =
1
>> B=2
B =
2
>> X = gaminv(P,A,B)
X =
0.2107 0.7133 1.8326 4.6052
Исследование влияния параметра A на вид обратной функции распределения вероятностей при В=1.
>> P=0:0.01:1;
>> B=1;
>> A=1;
>> X1 = gaminv(P,A,B);
>> A=2;
>> X2 = gaminv(P,A,B);
>> A=5;
>> X3 = gaminv(P,A,B);
>> plot(P,X1,'g',P,X2,'r',P,X3,'b')
>> grid on
Пример взаимосвязи между функцией распределения вероятностей и обратной функцией распределения.
>> x=1:5
x =
1 2 3 4 5
>> a = 1:5;
>> b = 6:10;
>> P= gamcdf(1:5,a,b);
>> X = gaminv(P,a,b)
>> x==X
ans =
1 1 1 1 1
geoinv - Обратная функция распределения вероятностей геометрического закона
Синтаксис:
X = geoinv(Y,P)
Описание:
geoinv(Y,P) возвращает ближайшее наименьшее положительное целое число, соответствующее равному или большему значению Y возвращаемому функцией распределения вероятностей геометрического закона при заданных X и Р. Параметр Y является вероятностью появления Х благоприятных исходов при независимых испытаниях, где Р – вероятность благоприятного исхода в одном опыте.
Размерность векторов или матриц Р и Y должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значения вероятностей Р и Y должны находиться в интервале [0 1].
Примеры:
Вероятность правильного предсказания результата 10 бросков монеты подряд составляет менее 0,001. Рассчитать значение квантили соответствующей указанной вероятности.
>> P=0.999;
>> p=0.5;
>> X= geoinv(P,p)
X =
9
Пример генерации псевдослучайных чисел распределенных по геометрическому закону обратным методом на основе использования обратной функции распределения.
>> X= rand(100,1);
>> Y= geoinv(X,0.5);
hygeinv - Обратная функция распределения вероятностей гипергеометрического закона
Синтаксис:
X = hygeinv(P,M,K,N)
Описание:
hygeinv(P,M,K,N) возвращает ближайшее наименьшее целое число, соответствующее равному или большему значению P возвращаемому функцией распределения вероятностей гипергеометрического закона при заданных значениях X, M, K, N. Параметр Р является вероятностью извлечь Х дефектных изделий при N опытах без последующего возврата из партии M штук в которой K изделий бракованные.
Примеры:
Рассмотрим решение задачи. Имеется производство гибких дисков партиями по 1000 штук в каждой. Контрольная выборка составляет 50 дисков из партии. Партия принимается, если в ней обнаруживается менее 10 бракованных дисков с 99% вероятностью. Определить допустимое число бракованных дисков в выборке?
Квантиль Х, соответствующая допустимому числу бракованных дисков в партии определяется как
>> N=50;
>> K=10;
>> M=1000;
>> P=0.99;
>> X = hygeinv(P,M,K,N)
X =
3
Чему равна медиана дефектных дисков в выборке из 50 единиц изделий из партии в 1000 штук? Число бракованных дисков в партии равно 10 изделиям.
>> N=50;
>> K=10;
>> M=1000;
>> P=0.5;
>> X = hygeinv(P,M,K,N)
X =
0
Определить зависимость допустимого числа бракованных дисков в выборке из 50 элементов от вероятности их обнаружения и размера партии.
>> N=50;
>> K=10;
>> M=1000;
>> P=0:0.01:1;
>> X1 = hygeinv(P,M,K,N);
>> M=2000;
>> X2 = hygeinv(P,M,K,N);
>> M=3000;
>> X3 = hygeinv(P,M,K,N);
>> plot(P,X1,’r’, P,X2,’g’, P,X3,’b’)
>> grid on
icdf - Обратные функции распределения случайных величин
Синтаксис
X = icdf('name',P,A1,A2,A3)
Описание
icdf('name',P,A1,A2,A3) возвращает значение квантили распределения для вероятности P и параметров 'name', A1, A2, A3. Строковая переменная 'name' задает вид распределения в соответствии со следующей таблицей
|
Вид распределения |
Переменная 'name' |
|
Бета |
'beta', 'Beta' |
|
Биномиальное |
'bino', 'Binomial' |
|
Хи-квадрат |
'chi2', 'Chisquare' |
|
Экспоненциальное |
'exp', 'Exponential' |
|
Фишера |
'f', 'F' |
|
Гамма |
'gam', 'Gamma' |
|
Геометрическое |
'geo', 'Geometric' |
|
Гипергеометрическое |
'hyge', 'Hypergeometric' |
|
Логнормальное |
'logn', 'Lognormal' |
|
Отрицательное биномиальное |
'nbin', 'Negative Binomial' |
|
Смещенное Фишера |
'ncf', 'Noncentral F' |
|
Смещенное Стьюдента |
'nct', 'Noncentral T' |
|
Смещенное хи-квадрат |
'ncx2', 'Noncentral Chi-square' |
|
Нормальное |
'norm', 'Normal' |
|
Пуассона |
'poiss', 'Poisson' |
|
Релея |
'rayl', 'Rayleigh' |
|
Стьюдента |
't', 'T' |
|
Дискретное равномерное |
'unid', 'Discrete Uniform' |
|
Непрерывное равномерное |
'unif', 'Uniform' |
|
Вейбулла |
'weib', 'Weibull' |
Параметры A1, A2, A3 являются параметрами перечисленных выше распределений. Последовательность и количество передаваемых параметров A1, A2, A3 должны соответствовать числу и последовательности передаваемым параметрам соответствующих функций распределения. Размерность векторов или матриц X, A1, A2, A3 должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
Примеры использования параметрической обратной функции распределения вероятностей
Использование обратной функции распределения нормального закона.
>> P=0:0.01:1;
>> MU=0;
>> SIGMA=1;
>> X1= icdf('Normal', P, MU, SIGMA);
>> SIGMA=2;
>> X2= icdf('Normal', P, MU, SIGMA);
>> SIGMA=3;
>> X3= icdf('Normal', P, MU, SIGMA);
>> plot(P,X1,'g',P,X2,'r',P,X3,'b')
>> grid on
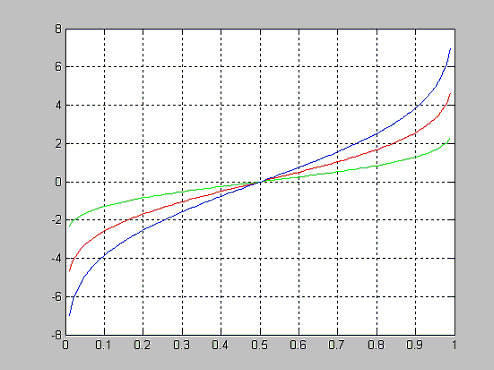
logninv - Обратная функция распределения вероятностей логнормального закона
Синтаксис:
X = logninv(P,MU,SIGMA)
Описание:
logninv(P,MU,SIGMA) служит для расчета квантили логнормального распределения при заданных математическом ожидании MU, среднем квадратическом отклонении SIGMA и вероятности Р. Размерность векторов или матриц P,MU,SIGMA должна быть одинаковой. Размерность скалярного параметра увеличивается до размера остальных входных аргументов. Среднее квадратическое отклонение SIGMA должно быть положительным числом. Значение вероятности P должно находиться в интервале [0 1].
Обратная функция распределения вероятностей логнормального закона имеет вид
![]() ,
,
где 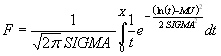 .
.
Примеры:
Использование скалярных аргументов P=0.5; MU=1; SIGMA=2.
>> P=0.5
P =
0.5000
>> MU=1
MU =
1
>> SIGMA=2
SIGMA =
2
>> X = logninv(P,MU,SIGMA)
X =
2.7183
Использование векторного аргумента P=[0 0,3 0,6 0,9]; и скалярных параметров MU=1; SIGMA=2.
>> P=[0 0.3 0.6 0.9]
P =
0 0.3000 0.6000 0.9000
>> MU=1
MU =
1
>> SIGMA=2
SIGMA =
2
>> X = logninv(P,MU,SIGMA)
X =
0 0.9524 4.5118 35.2725
Рассмотрим вид обратной функции распределения вероятностей логнормального закона в зависимости от значения SIGMA при постоянном MU=0.
>> P=0:0.01:1;
>> MU=0;
>> SIGMA=1;
>> X1 = logninv(P, MU, SIGMA);
>> SIGMA=2;
>> X2= logninv(P, MU, SIGMA);
>> SIGMA=3;
>> X3= logninv(P, MU, SIGMA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
nbininv - Обратная функция распределения вероятностей отрицательного биномиального закона
Синтаксис:
X = nbininv(Y,R,P)
Описание:
nbininv(Y,R,P) служит для расчета квантили отрицательного биномиального распределения с параметрами R,P и вероятности Y. Так как биномиальный закон описывает распределение дискретных случайных величин, nbininv возвращает ближайшее наименьшее целое число, соответствующее равному или большему значению Y возвращаемому функцией распределения вероятностей биномиального закона при заданных R и Р. Размерность векторов или матриц Y, R, P должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Простейшим случаем применения функции распределения вероятностей отрицательного биномиального закона является расчет числа удачных испытаний появления некоторого события при независимых испытаниях с постоянной вероятностью появления события в одном опыте Р. Число дополнительных испытаний Х, которое должно быть проведено, чтобы получить заданное число R успешных попыток имеет отрицательное биномиальное распределение. Более общая трактовка отрицательного биномиального распределения позволяет задавать параметр R как положительное вещественное число.
Примеры:
Рассмотрим решение следующей задачи. Сколько раз необходимо подбросить монету, чтобы с 99% вероятностью выпал “орел”?
Поскольку задача вписывается в модель отрицательного биномиального распределения, квантиль соответствующая заданной доверительной вероятности будет рассчитываться как
>> Y=0.99;
>> P=0.5;
>> R=10;
>> X= nbininv(Y,R,P) + 10
X =
33
Поскольку для того, чтобы получить не менее 10 наблюдений “орлов” необходимо подбросить монету 10 раз в правой части последнего выражения подставлено постоянное слагаемое.
Построим график зависимости числа опытов X от вероятности P.
>> Y=0.5:0.01:1;
>> P=0.5;
>> R=10;
>> X= nbininv(Y,R,P) + 10;
>> plot(Y,X)
>> grid on
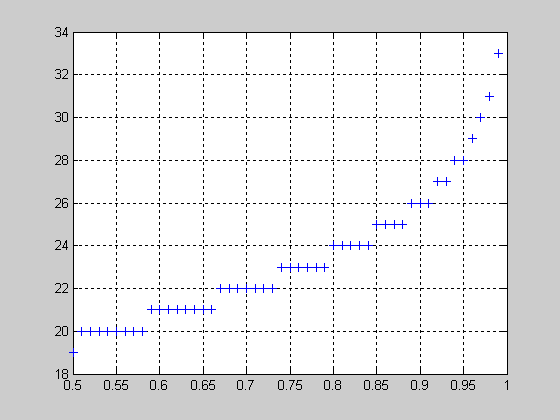
ncfinv - Обратная функция распределения вероятностей смещенного закона Фишера
Синтаксис:
X = ncfinv(P,NU1,NU2,DELTA)
Описание:
ncfinv(P,NU1,NU2,DELTA) позволяет рассчитать значения квантили Х смещенного закона Фишера для значений вероятности P, степеней свободы NU1, NU2 и положительного параметра смещения DELTA. Размерность векторов или матриц P, NU1, NU2, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
Примеры:
Использование скалярных аргументов P=0.1; NU1=5; NU2=8; DELTA=1.
>> P=0.1
P =
0.1000
>> NU1=5
NU1 =
5
>> NU2=8
NU2 =
8
>> DELTA=1
DELTA =
1
>> X = ncfinv(P,NU1,NU2,DELTA)
X =
0.3635
Использование векторной величины P=0:0.1:1 и скалярных аргументов NU1=5; NU2=8; DELTA=1.
>> P=0:0.1:1;
>> NU1=5;
>> NU2=8;
>> DELTA=1;
>> X = ncfinv(P,NU1,NU2,DELTA);
>> [X' P']
ans =
0 0
0.3635 0.1000
0.5500 0.2000
0.7302 0.3000
0.9229 0.4000
1.1430 0.5000
1.4103 0.6000
1.7610 0.7000
2.2795 0.8000
3.2629 0.9000
Inf 1.0000
Исследование влияния коэффициента смещения DELTA=[0 1 2] на вид обратной функции распределения вероятностей смещенного закона Фишера.
>> P=0:0.01:1;
>> NU1=5;
>> NU2=8;
>> DELTA=0;
>> X1 = ncfinv(P,NU1,NU2,DELTA);
>> DELTA=1;
>> X2 = ncfcdf(P,NU1,NU2,DELTA);
>> DELTA=2;
>> X3 = ncfcdf(P,NU1,NU2,DELTA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
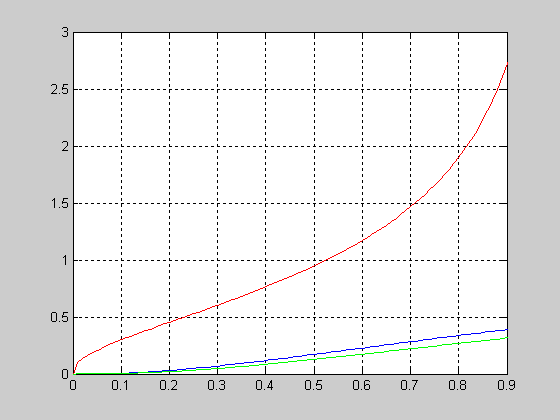
nctinv - Обратная функция распределения вероятностей смещенного закона Стьюдента (смещенного t распределения)
Синтаксис
X = nctinv(P,NU,DELTA)
Описание
nctinv(P,NU,DELTA) позволяет рассчитать значение квантили смещенного закона Стьюдента для значений вероятности P, степени свободы NU и параметра смещения DELTA. Размерность векторов или матриц P, NU, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента.
Примеры использования обратной функции распределения вероятностей смещенного закона Стьюдента
Расчет квантилей смещенного закона Стьюдента для вектора вероятностей P=[0,1 0,3 0,6 0,9] при NU=10 и DELTA=1.
>> P=[0.1 0.3 0.6 0.9]
P =
0.1 0.3000 0.6000 0.9000
>> NU=10
NU =
10
>> DELTA=1
DELTA =
1
>> X = nctinv(P,NU,DELTA)
X =
-0.2914 0.4846 1.2963 2.5261
Рассмотрим вид обратной функции распределения в зависимости от значения числа степеней свободы при постоянном DELTA=2.
>> P=0:0.01:1;
>> DELTA=2;
>> NU=10;
>> X1 = nctinv(P,NU,DELTA);
>> NU=20;
>> X2 = nctinv(P,NU,DELTA);
>> NU=30;
>> X3 = nctinv(P,NU,DELTA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
Влияние параметра смещения на вид обратной функции распределения
>> P=0:0.01:1;
>> NU=20;
>> DELTA =1;
>> X1 = nctinv(P,NU,DELTA);
>> DELTA =5;
>> X2 = nctinv(P,NU,DELTA);
>> DELTA =10;
>> X3 = nctinv(P,NU,DELTA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
ncx2inv - Обратная функция вероятностей смещенного распределения хи-квадрат
Синтаксис
X = ncx2inv(P,V,DELTA)
Описание
ncx2inv(P,V,DELTA) служит для расчета значений квантили смещенного распределения хи-квадрат для значения вероятности Р, степени свободы V и параметра смещения DELTA. Размерность векторов или матриц Р, V, DELTA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов. При расчете квантили Х в функции ncx2inv используется метод Ньютона
Примеры использования обратной функции распределения вероятностей смещенного закона Стьюдента
Расчет квантилей смещенного закона хи-квадрат для вектора вероятностей P=[0,1 0,3 0,6 0,9] и V=10 и DELTA=1.
>> P=[0.1 0.3 0.6 0.9]
P =
0.1 0.3000 0.6000 0.9000
>> V=10
V =
10
>> DELTA=1
DELTA =
1
>> X = ncx2inv(P,V,DELTA)
X =
5.3658 8.0074 11.5261 17.5606
Рассмотрим вид обратной функции распределения в зависимости от значения числа степеней свободы при постоянном DELTA=2.
>> P=0:0.01:1;
>> P=0:0.01:1;
>> DELTA=2;
>> V=10;
>> X1 = ncx2inv(P,V,DELTA);
>> V=20;
>> X2 = ncx2inv(P,V,DELTA);
>> V=30;
>> X3 = ncx2inv(P,V,DELTA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
Влияние параметра смещения на вид обратной функции распределения
>> P=0:0.01:1;
>> P=0:0.01:1;
>> V=20;
>> DELTA =1;
>> X1 = ncx2inv(P,V,DELTA);
>> DELTA =5;
>> X2 = ncx2inv(P,V,DELTA);
>> DELTA =10;
>> X3 = ncx2inv(P,V,DELTA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
norminv - Обратная функция распределения вероятностей нормального закона
Синтаксис
X = norminv(P,MU,SIGMA)
Описание
norminv(P,MU,SIGMA) служит для расчета значений квантили нормального закона для значений вероятности Р, математического ожидания MU и среднего квадратического отклонения SIGMA. Размерность векторов или матриц Р, MU, SIGMA должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение среднего квадратического отклонения SIGMA должно быть положительным. Значение вероятности P должно находиться в интервале [0 1].
Обратная функция распределения вероятностей нормального закона имеет вид
![]()
где 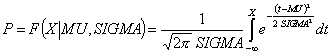
Квантиль Х является результатом решения приведенного интегрального уравнения равного значению вероятности Р при заданных параметрах нормального закона распределения MU, SIGMA.
Примеры использования обратной функции распределения вероятностей нормального закона
Определить интервал значений случайной величины Х распределенной по стандартному нормальному закону, симметричный относительно математического ожидания, соответствующий 95% доверительной вероятности.
Значение вероятностей соответствующие левой и правой границам интервала.
>> PLeft=(1-0.95)/2
PLeft =
0.0250
>> PRight=0.95+(1-0.95)/2
PRight =
0.9750
Параметры стандартного нормального распределения
>> MU=0;
>> SIGMA=1;
>> X = norminv([PLeft PRight], MU, SIGMA)
X =
-1.9600 1.9600
Графическое представление интервала.
>> X=-3:0.01:3;
>> MU=0;
>> SIGMA=1;
>> Xint = norminv([PLeft PRight], MU, SIGMA);
>> f=normpdf(X, MU, SIGMA);
>> t=unifpdf(X, Xint(1), Xint(2));
>> plot(X,f,X,t)
>> grid on
poissinv - Обратная функция распределения вероятностей закона Пуассона
Синтаксис
X = poissinv(P,LAMBDA)
Описание
poissinv(P,LAMBDA) возвращает минимальное значение Х, для которого интегральная вероятность рассчитанная по функции распределения Пуассона больше или равна значению Р. Значение вероятности P должно находиться в интервале [0 1].
Примеры использования обратной функции распределения вероятностей
Рассмотрим решение следующей задачи. Среднее количество дефектов LAMBDA в изделии равно 2. Определить 95% процентиль количества дефектов.
>> LAMBDA=2;
>> P=0.95;
>> X = poissinv(P,LAMBDA)
X =
5
Рассчитать медиану количества дефектов.
>> LAMBDA=0.5;
>> P=0.95;
>> X = poissinv(P,LAMBDA)
X =
2
Вид функции количества дефектов в зависимости от среднего количества дефектов на одно изделие LAMBDA и вероятности их возникновения.
>> P=0:0.01:1;
>> LAMBDA =2;
>> X1 = poissinv(P,LAMBDA);
>> LAMBDA =5;
>> X2 = poissinv(P,LAMBDA);
>> LAMBDA =10;
>> X3 = poissinv(P,LAMBDA);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
raylinv - Обратная функция распределения вероятностей закона Релея
Синтаксис
X = raylinv(P,B)
Описание
raylinv(P,B) служит для расчета значений квантили закона Релея для значений вероятности Р и параметра B. Размерность векторов или матриц Р и B должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение вероятности P должно находиться в интервале [0 1].
Примеры использования функции распределения вероятностей закона Релея
Расчет квантилей закона Релея для вектора вероятностей P=[0,1 0,3 0,6 0,9] при B=10.
>> P=[0.1 0.3 0.6 0.9]
P =
0.1 0.3000 0.6000 0.9000
>> B=10
B =
10
>> X = raylinv(P,B)
X =
4.5904 8.4460 13.5373 21.4597
Рассмотрим вид обратной функции распределения в зависимости от значения параметра В.
>> P=0:0.01:1;
>> B=2;
>> X1 = raylinv(P,B);
>> B=5;
>> X2 = raylinv(P,B);
>> B=10;
>> X3 = raylinv(P,B);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
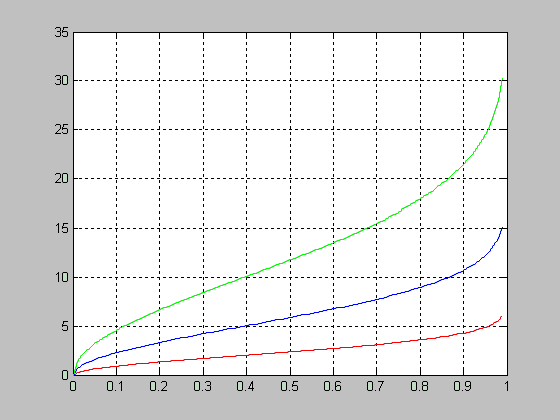
tinv - Обратная функция распределения вероятностей закона Стьюдента
Синтаксис
X = tinv(P,V)
Описание
tinv(P,V) служит для расчета значений квантили закона Стьюдента для значений вероятности P и степени свободы V. Размерность векторов или матриц P, V должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого входного аргумента. Значение числа степеней свободы V должно быть положительным целым числом. Значение вероятности P должно находиться в интервале [0 1].
Вид обратной функции распределения вероятностей закона Стьюдента
![]()
где 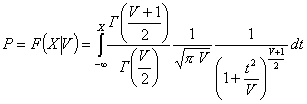
Квантиль Х является результатом решения интегрального уравнения равного Р при заданном числе степеней свободы.
Примеры использования обратной функции распределения вероятностей
Рассчитать 99% процентиль t распределения со степенями свободы от 1 до 6.
>> V=1:6;
>> P=0.99;
>> percentile = tinv(P,V)
percentile =
31.8205 6.9646 4.5407 3.7469 3.3649 3.1427
Зависимость обратной функции распределения от числа степеней свободы.
>> P=0:0.01:1;
>> V=2;
>> X1 = tinv(P,V);
>> V=5;
>> X2 = tinv(P,V);
>> V=20;
>> X3 = tinv(P,V);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
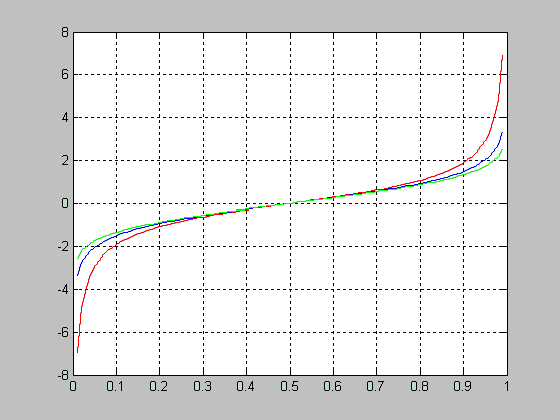
unidinv - Обратная функция распределения вероятностей дискретного равномерного распределения
Синтаксис
X = unidinv(P,N)
Описание
unidinv(P,N) возвращает минимальное положительное целое Х, для которого функция распределения вероятностей дискретного равномерного распределения возвращает значение вероятности равное или большее величины Р при заданном параметре N.
Размерность векторов или матриц Р и N должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности другого аргумента. Значение параметра N должно быть целым и положительным. Значение вероятности P должно находиться в интервале [0 1].
Примеры использования обратной функции распределения вероятностей дискретного равномерного распределения
Расчет квантилей дискретного равномерного закона для вектора вероятностей P=[0,1 0,3 0,6 0,9] при N=10.
>> P=[0.1 0.3 0.6 0.9]
P =
0.1 0.3000 0.6000 0.9000
>> NU=10
NU =
10
>> X = unidinv(P,N)
X =
1 3 6 9
Рассмотрим вид обратной функции распределения в зависимости от значения параметра N.
>> P=0:0.1:1;
>> N=10;
>> X1 = unidinv(P,N);
>> N=20;
>> X2 = unidinv(P,N);
>> N=30;
>> X3 = unidinv(P,N);
>> plot(P,X1,'o',P,X2,'.',P,X3,'+')
>> grid on
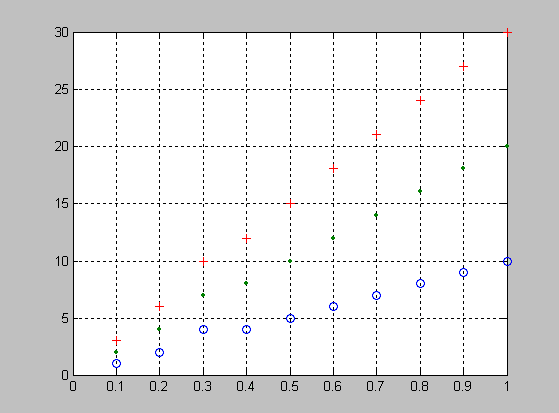
unifinv - Обратная функция распределения вероятностей непрерывного равномерного закона
Синтаксис
X = unifinv(P,A,B)
Описание
unifinv(P,A,B) возвращает значение квантили непрерывного равномерного закона для вероятности Р и параметров A, B. Размерность векторов или матриц Р, A, B должна быть одинаковой. Размерность скалярного параметра увеличивается до размерностей других аргументов. Верхний предел распределения B должен быть больше нижнего предела A. Значение вероятности P должно находиться в интервале [0 1].
Вид обратной функции распределения вероятностей непрерывного равномерного закона
![]()
где ![]() .
.
Стандартное непрерывное равномерное распределение имеет следующие параметры A=0, B=1.
Примеры использования обратной функции распределения вероятностей
Расчет медианы стандартного непрерывного равномерного распределения.
>> A=0;
>> B=1;
>> P=0.5;
>> median = unifinv(P,A,B)
median =
0.5000
Расчет 99% процентили непрерывного равномерного распределения с параметрами A=-1, B=1.
>> A=-1;
>> B=1;
>> P=0.99;
>> unifinv(P,A,B)
ans =
0.9800
Вид обратной функции распределения непрерывного равномерного распределения.
>> P=0:0.01:1;
>> A=-1;
>> B=1;
>> X1 = unifinv(P,A,B);
>> A=-2;
>> B=2;
>> X2 = unifinv(P,A,B);
>> A=-3;
>> B=3;
>> X3 = unifinv(P,A,B);
>> plot(P,X1,'r',P,X2,'b',P,X3,'g')
>> grid on
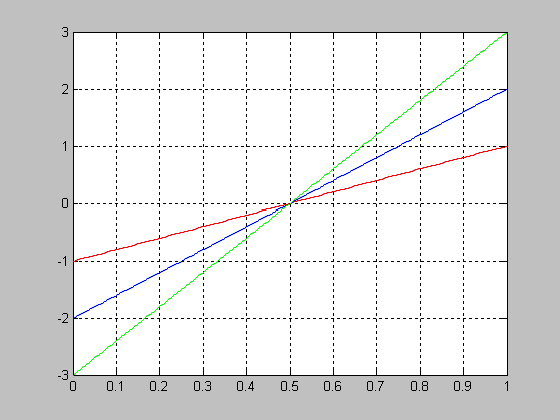
weibinv - Обратная функция распределения вероятностей закона Вейбулла
Синтаксис
X = weibinv(P,A,B)
Описание
weibinv(P,A,B) служит для расчета значений квантили закона Вейбулла для вероятности Р и параметров A, B. Размерность векторов или матриц Р, A, B должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных параметров. Значения величин A и B должны быть положительными. Значение вероятности P должно находиться в интервале [0 1].
Вид обратной функции распределения вероятностей закона Вейбулла
Примеры использования обратной функции распределения вероятностей закона Вейбулла
Рассмотрим решение следующей задачи. Время безотказной работы электрических ламп распределено по закону Вйбулла с параметрами A=0,15 и B=0,24. Рассчитать медиану времени безотказной работы изделий в партии.
>> A=0.15;
>> B=0.24;
>> P=0.5;
>> median= weibinv(P,A,B)
median =
588.4721
Рассчитать 90% процентиль времени безотказной работы изделий в партии.
>> A=0.15;
>> B=0.24;
>> P=0.9;
>> weibinv(P,A,B)
ans =
8.7536e+004
Зависимость времени безотказной работы изделий в от параметров A и B партии.
Зависимость времени безотказной работы изделий в от параметров A и B партии.
>> A=0.15;
>> B=0.24;
>> P=0:0.01:1;
>> X= weibinv(P,A,B);
>> subplot(2,2,1)
>> plot (P,X)
>> grid on
>> [A P] = meshgrid([0.1:0.1:2], [0:0.05:1]);
>> B=2;
>> X = weibinv(P,A,B);
>> subplot(2,2,2)
>> surf(A,P,X)
>> [B P] = meshgrid([0.1:0.1:2], [0:0.05:1]);
>> A=5;
>> X = weibinv(P,A,B);
>> subplot(2,2,3)
>> surf(B,P,X)
>> [B A] = meshgrid([0.1:0.1:2], [1:0.2:5]);
>> P=0.5;
>> X = weibinv(P,A,B);
>> subplot(2,2,4)
>> surf(B,A,X)
binornd - Функция генерации псевдослучайных чисел распределенных по биномиальному закону
Синтаксис
R = binornd(N,P)
R = binornd(N,P,m)
R = binornd(N,P,m,n)
Описание
R = binornd(N,P) функция предназначена для генерации псевдослучайного числа распределенного по биномиальному закону для пары параметров N и P. Размерность векторов или матриц параметров N и P должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов.
R = binornd(N,P,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по биномиальному закону для параметров N и P, где m - вектор размерностью 1![]() 2 определяющий размерность матрицы R.
2 определяющий размерность матрицы R.
R = binornd(N,p,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по биномиальному закону для параметров N и P.
При генерации псевдослучайных чисел используется прямой метод, работающий согласно определению биномиального закона как суммы случайных чисел Бернулли.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенной паре параметров N и P.
>> N=100;
>> P=0.5;
>> R = binornd(N,P)
R =
53
>> N=[10 20 30 40 50];
>> P=[0.2 0.3 0.5 0.7 0.9];
>> R = binornd(N,P)
R =
2 5 12 21 41
Генерация вектора с размерностью 1![]() 5 элементов псевдослучайных чисел.
5 элементов псевдослучайных чисел.
>> N=100;
>> P=0.5;
>> m=[1 5];
>> R = binornd(N,P,m)
R =
44 53 47 55 49
Другой вариант генерации вектора с размерностью 1![]() 5.
5.
>> N=100;
>> P=0.5;
>> m=1; n=5;
>> R = binornd(N,P,m,n)
R =
48 47 52 49 45
Генерация матрицы с размерностью 5![]() 5 элементов.
5 элементов.
>> N=100;
>> P=0.5;
>> m=[5 5];
>> R = binornd(N,P,m)
R =
45 46 44 44 51
51 51 49 48 48
53 51 47 52 45
46 53 48 53 53
53 59 52 51 53
Другой вариант генерации матрицы с размерностью 5![]() 5.
5.
>> N=100;
>> P=0.5;
>> m=5; n=5;
>> R = binornd(N,P,m,n)
R =
37 45 50 50 47
49 41 45 42 53
44 40 48 41 49
50 45 46 45 52
52 48 50 56 55
Оценка качества генерации псевдослучайных чисел в виде наложения гистограммы и функции случайной величины, приведенной к абсолютному масштабу.
>> N=100;
>> P=0.5;
>> N=9;
>> R = binornd(N,P,[1 100]);
>> hist(R, N)
>> grid on
>> X=floor(min(R)):1: floor (max(R));
>> f=binopdf(X,N,P);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
chi2rnd - Функция генерации псевдослучайных чисел распределенных по закону хи-квадрат
Синтаксис
R = chi2rnd(V)
R = chi2rnd(V,m)
R = chi2rnd(V,m,n)
Описание
R = chi2rnd(V) функция предназначена для генерации псевдослучайного числа распределенного по закону хи-квадрат для каждого значения параметра V.
R = chi2rnd(V,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону хи-квадрат для параметра V, где m - вектор размерностью 1![]() 2 определяющий размерность матрицы R.
2 определяющий размерность матрицы R.
R = chi2rnd(V,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону хи-квадрат для параметра V.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра V.
>> V=10;
>> R = chi2rnd(V)
R =
4.4268
>> V=[10 20 30 40 50];
>> R = chi2rnd(V)
R =
13.9829 23.2734 26.5743 29.3867 57.3204
Генерация вектора с размерностью 1![]() 5 элементов псевдослучайных чисел.
5 элементов псевдослучайных чисел.
>> V=10;
>> m=[1 5];
>> R = chi2rnd(V,m)
R =
10.2302 15.6096 9.4732 3.3293 9.2048
Другой вариант генерации вектора с размерностью 1![]() 5.
5.
>> V=10;
>> m=1; n=5;
>> R = chi2rnd(V,m,n)
R =
3.6552 11.6533 13.8338 9.8985 10.0190
Генерация матрицы с размерностью 5![]() 5 элементов.
5 элементов.
>> V=10;
>> m=[5 5];
>> R = chi2rnd(V,m)
R =
16.7829 9.0128 6.9741 14.9470 5.1372
11.1580 7.5976 6.8432 10.2689 11.8798
10.9589 6.5304 14.8066 11.7760 14.8122
8.5577 10.9080 9.5915 10.6171 9.9286
5.8218 9.3833 13.1405 5.1395 6.5166
Другой вариант генерации матрицы с размерностью 5![]() 5.
5.
>> V=10;
>> m=5; n=5;
>> R = chi2rnd(V,m,n)
R =
8.0671 5.7285 5.6716 6.3146 4.3965
15.8682 5.2127 11.7063 6.7905 8.6128
7.5513 29.6239 6.7613 5.0805 13.1623
4.6136 7.9643 6.3317 7.4396 9.4257
11.1463 12.4863 9.4614 6.4557 13.1582
Оценка качества генерации псевдослучайных чисел в виде наложения гистограммы и функции случайной величины,
приведенной к абсолютному масштабу.
>> V=10;
>> N=9;
>> R = chi2rnd(V,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= chi2pdf(X, V);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
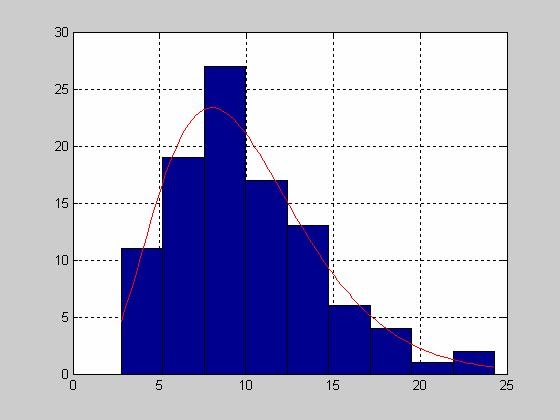
exprnd - Функция генерации псевдослучайных чисел распределенных по экспоненциальному закону
Синтаксис
R = exprnd(MU)
R = exprnd(MU,m)
R = exprnd(MU,m,n)
Описание
R = exprnd(MU) функция предназначена для генерации псевдослучайного числа распределенного по экспоненциальному закону для каждого значения параметра MU.
R = exprnd(MU,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по экспоненциальному закону для параметра MU, где m - вектор размерностью 1![]() 2 определяющий размерность матрицы R.
2 определяющий размерность матрицы R.
R = exprnd(MU,m,n) генерирует матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по экспоненциальному закону для параметра MU.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра MU.
>> MU=0.4;
>> R = exprnd(MU)
R =
1.8538
>> MU =[0.1 0.2 0.3 0.4 0.5];
>> R = exprnd(MU)
R =
0.1132 0.2735 0.1867 0.2105 0.3610
Генерация вектора с размерностью 1![]() 5 элементов псевдослучайных чисел.
5 элементов псевдослучайных чисел.
>> MU=0.4;
>> m=[1 5];
>> R = exprnd(MU,m)
R =
0.2396 0.3699 0.2204 0.5180 0.0768
Другой вариант генерации вектора с размерностью 1![]() 5.
5.
>> MU=0.4;
>> m=1; n=5;
>> R = exprnd(MU,m,n)
R =
0.1983 0.2589 0.1295 0.2067 0.0532
Генерация матрицы с размерностью 5![]() 5 элементов.
5 элементов.
>> MU=0.4;
>> m=[5 5];
>> R = exprnd(MU,m)
R =
0.8634 1.0390 0.2762 0.0600 0.0560
0.2429 0.0204 0.0665 1.0089 0.3951
0.3584 0.4299 0.1137 0.4523 0.8419
0.1864 0.1511 0.3710 0.9521 0.8141
0.0849 0.3976 0.1848 0.2448 0.1543
Другой вариант генерации матрицы с размерностью 5![]() 5.
5.
>> MU=0.4;
>> m=5; n=5;
>> R = exprnd(MU,m,n)
R =
0.0352 0.0924 0.4238 0.1251 0.1011
1.1498 0.6030 0.2987 0.1278 0.1153
0.2855 0.3076 0.3149 1.4147 0.0581
0.3950 0.0745 0.6821 1.0687 0.8324
0.0582 0.2488 0.1619 1.0534 0.8260
Оценка качества генерации псевдослучайных чисел в виде наложения гистограммы и функции случайной величины,
приведенной к абсолютному масштабу.
>> MU=0.4;
>> N=9;
>> R = exprnd(MU,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= exppdf(X, MU);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
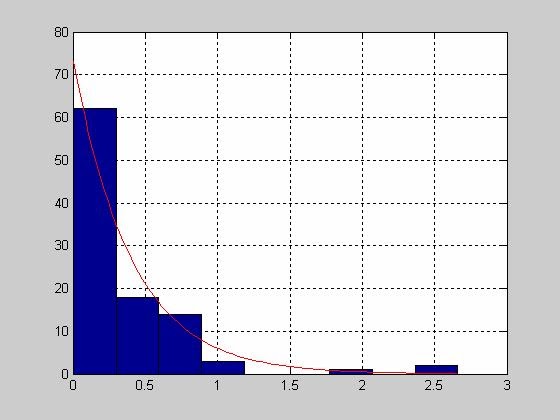
frnd - Функция генерации псевдослучайных чисел распределенных по закону Фишера
Синтаксис
R = frnd(V1,V2)
R = frnd(V1,V2,m)
R = frnd(V1,V2,m,n)
Описание
R = frnd(V1,V2) функция предназначена для генерации псевдослучайного числа распределенного по закону Фишера для пары параметров V1 и V2. Размерность векторов или матриц параметров V1 и V2 должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов.
R = frnd(V1,V2,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону Фишера для параметров V1 и V2, где m - вектор размерностью 1![]() 2 определяющий размерность матрицы R.
2 определяющий размерность матрицы R.
R = frnd(V1,V2,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Фишера для параметров V1 и V2.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенной паре параметров V1 и V2.
>> V1=10;
>> V2=20;
>> R = frnd(V1,V2)
R =
0.6319
>> V1=[10 20 30 40 50];
>> V2=[10 30 50 80 100];
>> R = frnd(V1,V2)
R =
2.0895 1.6933 1.0552 1.1905 0.7795
Генерация вектора с размерностью 1![]() 5 элементов псевдослучайных чисел.
5 элементов псевдослучайных чисел.
>> V1=10;
>> V2=20;
>> m=[1 5];
>> R = frnd(V1,V2,m)
R =
0.7154 0.3459 2.2092 0.5791 2.1545
Другой вариант генерации вектора с размерностью 1![]() 5.
5.
>> V1=10;
>> V2=20;
>> m=1; n=5;
>> R = frnd(V1,V2,m,n)
R =
1.2178 0.3249 0.6064 1.1579 0.9735
Генерация матрицы с размерностью 5![]() 5 элементов.
5 элементов.
>> V1=10;
>> V2=20;
>> m=[5 5];
>> R = frnd(V1,V2,m)
R =
1.1582 1.3797 0.4500 1.2340 0.6276
0.6548 0.5900 1.9506 0.2532 0.7807
0.2285 0.5503 1.0314 0.6213 0.5680
2.2817 1.6037 0.6418 2.0780 1.0944
0.9668 0.3549 0.3285 1.1812 1.8151
Другой вариант генерации матрицы с размерностью 5![]() 5.
5.
>> V1=10;
>> V2=20;
>> m=5; n=5;
>> R = frnd(V1,V2,m,n)
R =
1.4194 0.4185 0.8417 1.0677 0.5653
0.9864 1.0538 0.7662 0.5136 0.6978
0.9604 0.4686 1.7265 1.1150 2.4472
0.9208 0.5839 3.3868 1.0073 0.5485
1.0748 0.4043 1.9881 0.6960 0.9183
Оценка качества генерации псевдослучайных чисел в виде наложения гистограммы и функции случайной величины,
приведенной к абсолютному масштабу.
>> V1=10;
>> V2=20;
>> N=9;
>> R = frnd(V1,V2,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f=fpdf(X, V1,V2);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
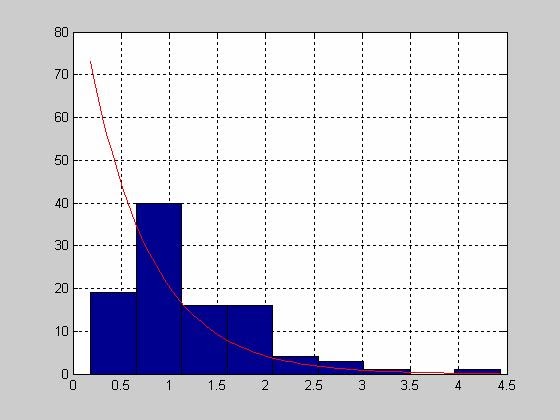
gamrnd - Функция генерации псевдослучайных чисел по Гамма распределению
Синтаксис
R = gamrnd(A,B)
R = gamrnd(A,B,m)
R = gamrnd(A,B,m,n)
Описание
R = gamrnd(A,B) функция предназначена для генерации псевдослучайного числа по Гамма распределению для каждой пары параметров A и B. Размерность векторов или матриц параметров A и B должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов.
R = gamrnd(A,B,m) позволяет получить вектор псевдослучайных чисел на m элементов по Гамма распределению для параметров A и B.
R = gamrnd(A,B,m,n) ) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов по Гамма распределению для параметров A и B.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего заданной паре значений параметров A и B.
>> A=1;
>> B=2;
>> R = gamrnd(A,B)
R =
0.1023
>> A=[1 2 3 4 5];
>> B=5;
>> R = gamrnd(A,B)
R =
7.3237 7.5060 9.5972 36.0827 31.6181
Генерация вектора псевдослучайных чисел с размерностью 1![]() 4.
4.
>> A=5;
>> B=7;
>> m=[1 4];
>> R = gamrnd(A,B,m)
R =
34.2698 47.0043 23.1796 42.3183
Второй вариант генерации вектора с размерностью 1![]() 4.
4.
>> A=1;
>> B=3;
>> m=1; n=5;
>> R = gamrnd(A,B,m,n)
R =
8.5476 3.1250 0.6205 13.8574 5.9222
Генерация матрицы псевдослучайных чисел с размерностью 4![]() 4.
4.
>> A=2;
>> B=3;
>> m=[4 4];
>> R = gamrnd(A,B,m)
R =
10.1321 2.9526 14.7757 3.3462
9.8778 12.1505 2.5314 8.7751
4.4587 6.9010 1.8665 5.5206
4.3094 2.2406 9.5973 9.3098
Другой вариант генерации матрицы с размерностью 4![]() 4.
4.
>> A=1;
>> B=3;
>> m=4; n=4;
>> R = gamrnd(A,B,m,n)
R =
1.8816 1.6965 2.4299 0.1323
0.9560 2.9794 1.0934 1.9469
3.5204 1.0583 1.4278 0.3830
0.5284 1.8123 0.6889 5.2642
Графическая оценка качества генератора псевдослучайных чисел
>> A=1;
>> B=3;
>> N=9;
>> R = gamrnd(A,B,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= gampdf(X, A,B);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
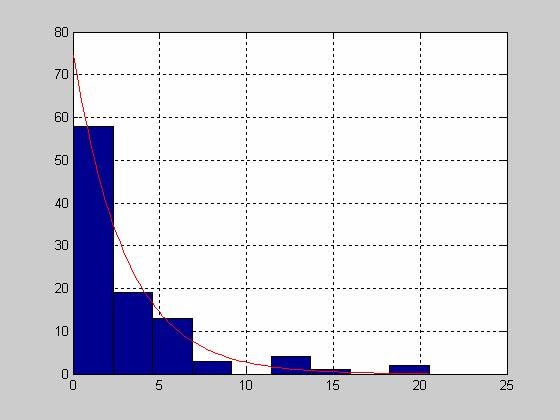
geornd - Функция генерации псевдослучайных чисел распределенных по геометрическому закону
Синтаксис
R = geornd(P)
R = geornd(P,m)
R = geornd(P,m,n)
Описание
R = geornd(P) функция предназначена для генерации псевдослучайного числа распределенного по геометрическому закону для каждого значения параметра P.
R = geornd(P,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по геометрическому закону для параметра P.
R = geornd(P,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по геометрическому закону для параметра P.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра P.
>> P=0.4;
>> R = geornd(P)
R =
2
>> P =[0.1 0.2 0.3 0.4 0.5];
>> R = geornd(P)
R =
13 0 0 3 6
Генерация вектора с размерностью 1![]() 5 элементов псевдослучайных чисел.
5 элементов псевдослучайных чисел.
>> P=0.4;
>> m=[1 5];
>> R = geornd(P,m)
R =
0 3 2 0 2
Другой вариант генерации вектора с размерностью 1![]() 5.
5.
>> P=0.4;
>> m=1; n=5;
>> R = geornd(P,m,n)
R =
1 5 0 1 1
Генерация матрицы с размерностью 5![]() 5 элементов.
5 элементов.
>> P=0.4;
>> m=[5 5];
>> R = geornd(P,m)
R =
1 0 0 5 0
2 1 0 0 8
1 0 1 5 0
2 3 1 1 0
1 1 0 2 0
Другой вариант генерации матрицы с размерностью 5![]() 5.
5.
>> P=0.4;
>> m=5; n=5;
>> R = geornd(P,m,n)
R =
0 2 2 0 0
1 0 1 0 1
1 0 0 3 1
3 1 0 3 1
0 0 3 0 6
Графическая оценка качества генератора псевдослучайных чисел
>> P=0.4;
>> N=9;
>> R = geornd(P,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):1:max(R);
>> f= geopdf(X, P);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
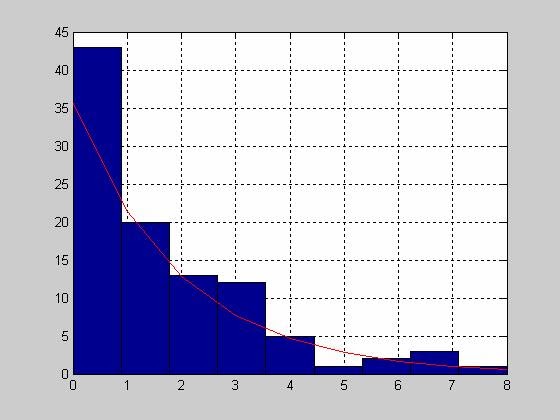
hygernd - Функция генерации псевдослучайных чисел распределенных по гипергеометрическому закону
Синтаксис
R = hygernd(M,K,N)
R = hygernd(M,K,N,m)
R = hygernd(M,K,N,m,n)
Описание
R = hygernd(M,K,N) функция предназначена для генерации псевдослучайного числа распределенного по гипергеометрическому закону для сочетания параметров M, K, N. Размерность векторов или матриц параметров M, K, N должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов.
R = hygernd(M,K,N,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по гипергеометрическому закону для параметров M, K, N.
R = hygernd(M,K,N,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по гипергеометрическому закону для параметров M, K, N.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному сочетанию параметров M, K, N.
>> M=50;
>> N=20;
>> K=7;
>> R = hygernd(M,K,N)
R =
3
>> M=[100 200 300 400 500];
>> N=[10 30 50 80 100];
>> K=[5 10 30 60 80];
>> R = hygernd(M,K,N)
R =
0 0 5 13 9
Генерация вектора с размерностью 1![]() 5 элементов псевдослучайных чисел.
5 элементов псевдослучайных чисел.
>> M=50;
>> N=20;
>> K=7;
>> m=[1 5];
>> R = hygernd(M,K,N,m)
R =
0 2 3 1 2
Другой вариант генерации вектора с размерностью 1![]() 5.
5.
>> M=50;
>> N=20;
>> K=7;
>> m=1; n=5;
>> R = hygernd(M,K,N,m,n)
R =
3 3 3 1 3
Генерация матрицы с размерностью 5![]() 5 элементов.
5 элементов.
>> M=50;
>> N=20;
>> K=7;
>> m=[5 5];
>> R = hygernd(M,K,N,m)
R =
3 4 3 2 1
2 3 4 4 1
2 3 2 4 3
3 1 2 2 2
3 3 4 2 4
Другой вариант генерации матрицы с размерностью 5![]() 5.
5.
>> M=50;
>> N=20;
>> K=7;
>> m=5; n=5;
>> R = hygernd(M,K,N,m,n)
R =
2 2 1 2 3
2 2 3 4 4
6 2 4 2 0
3 3 5 3 1
2 1 2 5 4
Графическая оценка качества генератора псевдослучайных чисел
>> M=50;
>> N=20;
>> K=7;
>> R = hygernd(M,K,N,[1 100]);
>> hist(R, 9)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f=hygepdf(X,M,K,N);
>> ff=f*100*((max(R)-min(R))/9);
>> hold on
>> plot(X,ff,'r')
>> hold off
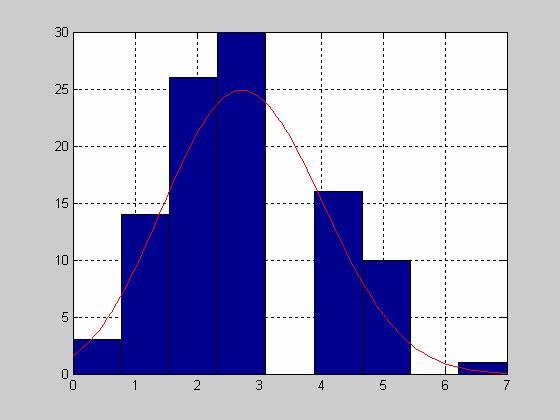
iwishrnd - Функция генерации псевдослучайных чисел по обратному распределению Уишарта
Синтаксис
W=iwishrnd(SIGMA,df)
W=iwishrnd(SIGMA,df,DI)
[W,DI]=iwishrnd(SIGMA,df)
Описание
W=iwishrnd(SIGMA,df) служит для генерации матицы случайных чисел распределенных по обратному распределению Уишарта для ковариационной матрицы inv(SIGMA) с числом степеней свободы df.
W=iwishrnd(SIGMA,df,DI) в отличии от предыдущего варианта синтаксиса задается коэффициент Холецкого DI обратной ковариационной матрицы.
[W,DI]=iwishrnd(SIGMA,df) в отличии от первого варианта вызова функции кроме матрицы псевдослучайных чисел W возвращается значение коэффициента Холецкого DI, который может быть использован при последующих вызовах функции iwishrnd.
Примеры использования функции генерации псевдослучайных чисел
Генерация псевдослучайных чисел по обратному распределению Уишарта.
>> SIGMA=pascal(3)
SIGMA =
1 1 1
1 2 3
1 3 6
>> df=5
df =
5
>> W=iwishrnd(A,df)
W =
0.6011 0.1055 0.0229
0.1055 2.1282 0.8601
0.0229 0.8601 0.3753
Генерация псевдослучайных чисел по обратному распределению Уишарта и расчет коэффициента Холецкого DI.
>> SIGMA=pascal(3)
SIGMA =
1 1 1
1 2 3
1 3 6
>> df=5
df =
5
>> [W,DI]=iwishrnd(SIGMA,df)
W =
2.4815 2.2623 0.5948
2.2623 3.6664 1.5391
0.5948 1.5391 0.7814
DI =
1 -1 1
0 1 -2
0 0 1
Расчет псевдослучайных чисел согласно обратному распределению Уишарта и использование коэффициента
Холецкого DI при повторной генерации.
>> SIGMA=pascal(5)
SIGMA =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
>> df=10
df =
10
>> [W,DI]=iwishrnd(SIGMA,df)
W =
1.2555 2.9061 3.6567 1.9071 0.3948
2.9061 7.5631 9.6383 5.1410 1.0714
3.6567 9.6383 13.0949 7.3482 1.5956
1.9071 5.1410 7.3482 4.3615 0.9920
0.3948 1.0714 1.5956 0.9920 0.2357
DI =
1 -1 1 -1 1
0 1 -2 3 -4
0 0 1 -3 6
0 0 0 1 -4
0 0 0 0 1
>> W=iwishrnd(SIGMA,df,DI)
W =
2.6936 1.6496 -0.7085 -1.4002 -0.4610
1.6496 7.8608 10.2487 6.1963 1.4143
-0.7085 10.2487 17.2284 11.7529 2.8645
-1.4002 6.1963 11.7529 8.3968 2.0935
-0.4610 1.4143 2.8645 2.0935 0.5297
lognrnd - Логнормальное распределение
Синтаксис
R = lognrnd(MU,SIGMA)
R = lognrnd(MU,SIGMA,m)
R = lognrnd(MU,SIGMA,m,n)
Описание
R = lognrnd(MU,SIGMA) функция предназначена для генерации псевдослучайного числа по логнормальному распределению с параметрами MU и SIGMA. Размерность векторов или матриц параметров MU и SIGMA должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Размерность R равна размерности векторов или матриц параметров MU и SIGMA.
R = lognrnd(MU,SIGMA,m) позволяет получить вектор псевдослучайных чисел на m элементов по логнормальному распределению с параметрами MU и SIGMA, где m - вектор размерностью 1![]() 2 определяющий размерность матрицы R.
2 определяющий размерность матрицы R.
R = lognrnd(MU,SIGMA,m,n) генерирует матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по логнормальному распределению с параметрами MU и SIGMA.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего заданной паре значений параметров MU, SIGMA.
>> MU =0;
>> SIGMA =1;
>> R = lognrnd(MU,SIGMA)
R =
0.6488
>> A=[1 2 3 4 5];
>> B=5;
>> R = gamrnd(A,B)
R =
7.3237 7.5060 9.5972 36.0827 31.6181
Генерация вектора псевдослучайных чисел с размерностью 1![]() 4.
4.
>> MU =0;
>> SIGMA =1;
>> m=[1 4];
>> R = lognrnd(MU,SIGMA,m)
R =
0.1891 1.1335 1.3333 0.3178
Второй вариант генерации вектора с размерностью 1![]() 4.
4.
>> MU =0;
>> SIGMA =1;
>> m=1; n=4;
>> R = lognrnd(MU,SIGMA,m,n)
R =
3.2901 3.2843 0.9631 1.3872
Генерация матрицы псевдослучайных чисел с размерностью 4![]() 4.
4.
>> MU =0;
>> SIGMA =1;
>> m=[4 4];
>> R = lognrnd(MU,SIGMA,m)
R =
1.1908 8.8745 1.0611 0.2628
0.8297 0.8725 0.9088 2.0428
2.0664 1.1207 0.4350 5.0711
0.5553 2.9060 1.3423 0.5007
Другой вариант генерации матрицы с размерностью 4![]() 4.
4.
>> MU =0;
>> SIGMA =1;
>> m=4; n=4;
>> R = lognrnd(MU,SIGMA,m,n)
R =
2.3584 1.7703 2.0379 0.3005
3.5043 0.6704 3.6337 0.9804
0.2032 1.9937 1.9515 0.8549
0.2367 2.2606 3.2898 0.2011
Графическая оценка качества генератора псевдослучайных чисел
>> MU =0;
>> SIGMA =1;
>> N=9;
>> R = lognrnd(MU,SIGMA,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= lognpdf(X,MU,SIGMA);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
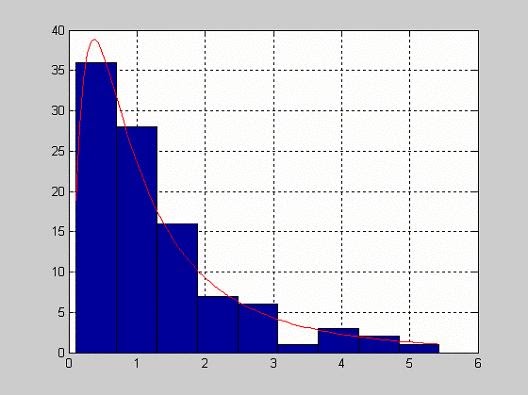
mvnrnd - Многомерное нормальное распределение
Синтаксис
R = mvnrnd(MU,SIGMA)
R = mvnrnd(MU,SIGMA,cases)
Описание
R = mvnrnd(MU,SIGMA) генерирует матрицу n-d псевдослучайных чисел распределенных по многомерному нормальному закону с параметрами математического ожидания MU и ковариации SIGMA. Размерность матрицы MU n-d. Функция mvnrnd генерирует каждый ряд R на основе соответствующего ряда значений MU. Матрица SIGMA должна быть квадратной и положительно определенной. SIGMA может быть задана матрицей с размерностью d-d или 3-х мерным массивом с размерностью d-d-n. Если SIGMA задана как 3-х мерный массив, то каждый ряд R генерируется с использованием страницы массива SIGMA, т.е. R(i,:) генерируется с использованием MU(i,:) и SIGMA(:,:,i). Если MU задан как вектор с размерностью 1-d, то функция mvnrnd формирует матрицу размерности соответствующей размерности SIGMA.
r = mvnrnd(MU,SIGMA,cases) генерирует матрицу псевдослучайных чисел с размерностью cases-d распределенных по многомерному нормальному распределению для вектора средних MU с размерностью 1-d и матрицы SIGMA с размерностью d-d.
Примеры использования функции генерации псевдослучайных чисел
Генерация псевдослучайных чисел по многомерному нормальному распределению.
>> MU=[0 1 2];
>> SIGMA=pascal(3)
SIGMA =
1 1 1
1 2 3
1 3 6
>> R = mvnrnd(MU,SIGMA)
R =
-0.8436 0.6541 3.6404
Генерация псевдослучайных чисел по многомерному нормальному распределению при условии, что SIGMA задана как 3-х мерный массив.
>> MU=[0 0 0; 1 1 1; 2 2 2];
>> SIGMA = cat(3, pascal(3), pascal(3) , pascal(3))
SIGMA(:,:,1) =
1 1 1
1 2 3
1 3 6
SIGMA(:,:,2) =
1 1 1
1 2 3
1 3 6
SIGMA(:,:,3) =
1 1 1
1 2 3
1 3 6
>> R = mvnrnd(MU,SIGMA)
R =
-0.3304 -0.8303 -1.3661
0.8252 -0.1320 0.2033
2.4409 3.7219 4.5051
Генерация двумерного нормального распределения и его графическое представление.
>> mu = [2 3];
>> sigma = [1 1.5; 1.5 3];
>> r = mvnrnd(mu,sigma,100);
>> plot(r(:,1),r(:,2),'+')
>> grid on
mvtrnd - Многомерное распределение Стьюдента
Синтаксис
r = mvtrnd(C,df,cases)
Описание
r = mvtrnd(C,df,cases) функция возвращает матрицу псевдослучайных чисел распределенных по многомерному распределению, где С - матрица коэффициентов корреляции, df - число степеней свободы, cases - число генерируемых значений. Параметры df и cases могут быть скалярными величинами или векторами с одинаковой размерностью. Например, если р - число столбцов матрицы С, то матрица r будет сгенерирована с размерностью cases рядов и р столбцов.
Распределение строки матрицы r соответствует отношению вектора значений распределенных по многомерному нормальному распределению со средним равным нулю, дисперсией равной 1 и ковариационной матрицей С, деленного на независимую случайную величину распределенную по закону хи-квадрат с числом степеней свободы df.
C должна бать квадратной, симметричной и положительно определенной матрицей. Если диагональные элементы матрицы С не равны 1, то такая матрица считается ковариационной и mvtrnd преобразует ее в матрицу коэффициентов корреляции перед началом генерации.
Примеры использования функции генерации псевдослучайных чисел
Генерация псевдослучайных чисел по многомерному t распределению.
>> df = 5;
>> С = [1 0.5;0.5 1];
>> cases = 5;
>> r = mvtrnd(C,df, cases)
r =
-0.8143 -3.5264
0.0171 0.2116
0.3297 0.7272
0.9883 0.4883
0.6443 0.9432
Генерация псевдослучайных чисел по многомерному t распределению при условии, что вместо матрицы коэффициентов корреляции задана ковариационная матрица.
>> df = 8;
>> C = [0.2 0.2; 0.2 0.4];
>> cases = 8;
>> r = mvtrnd(C,df, cases)
r =
0.0294 -1.1512
1.0211 0.5235
-1.7769 -1.8022
0.7687 -0.4725
-2.0229 -1.2128
-2.1397 -3.0752
0.5301 0.7748
-0.1257 -1.3711
Генерация двумерного t распределения и его графическое представление.
>> df = 3;
>> С = [1 0.8;0.8 1];
>> r = mvtrnd(C,df,100);
>> plot(r(:,1),r(:,2),'+')
>> grid on
nbinrnd - Отрицательное биномиальное распределение
Синтаксис
RND = nbinrnd(R,P)
RND = nbinrnd(R,P,m)
RND = nbinrnd(R,P,m,n)
Описание
RND = nbinrnd(R,P) функция предназначена для генерации псевдослучайного числа по отрицательному биномиальному распределению с параметрами R,P. Размерность векторов или матриц параметров R и P должна быть одинаковой. Скалярный параметр увеличивается до размера другого входного аргумента. Размерность вектора или матрицы RND соответствует размерности R и P.
RND = nbinrnd(R,P,m) позволяет получить вектор или матрицу псевдослучайных чисел на m элементов по отрицательному биномиальному распределению с параметрами P и R, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
RND = nbinrnd(R,P,m,n) генерирует матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по отрицательному биномиальному распределению с параметрами P и R.
Примеры использования функции генерации псевдослучайных чисел.
Генерация одного числа соответствующего определенной паре параметров R и P.
>> R=10;
>> P=0.5;
>> RND = nbinrnd(R,P)
RND =
4
>> R=[10 20 30 40 50];
>> P=[0.2 0.3 0.5 0.7 0.9];
>> RND = nbinrnd(R,P)
RND =
72 22 23 19 5
Генерация вектора с размерностью 1x5 элементов псевдослучайных чисел.
>> R=10;
>> P=0.5;
>> m=[1 5];
>> RND = nbinrnd(R,P,m)
RND =
4 4 10 6 5
Другой вариант генерации вектора с размерностью 1x5.
>> R=10;
>> P=0.5;
>> m=1; n=5;
>> RND = nbinrnd(R,P,m,n)
RND =
10 6 13 9 8
Генерация матрицы с размерностью 5x5 элементов.
>> R=10;
>> P=0.5;
>> m=[5 5];
>> RND = nbinrnd(R,P,m)
RND =
6 9 17 8 5
11 8 13 15 8
7 8 9 8 15
14 8 14 8 8
4 12 7 12 6
Другой вариант генерации матрицы с размерностью 5x5.
>> R=10;
>> P=0.5;
>> m=5; n=5;
>> RND = nbinrnd(R,P,m,n)
RND =
20 10 22 12 13
12 14 8 11 8
4 2 4 8 12
15 4 1 11 12
17 12 15 11 4
Оценка качества генерации псевдослучайных чисел в виде наложения гистограммы и функции случайной величины,
приведенной к абсолютному масштабу.
>> R=10;
>> P=0.5;
>> N=9;
>> RND = nbinrnd(R,P,[1 100]);
>> hist(RND, N)
>> grid on
>> X=floor(min(RND)):1: floor (max(RND));
>> f=nbinpdf(X,R,P);
>> ff=f*100*((max(RND)-min(RND))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
ncfrnd - Смещенное распределение Фишера
Синтаксис
R = ncfrnd(NU1,NU2,DELTA)
R = ncfrnd(NU1,NU2,DELTA,m)
R = ncfrnd(NU1,NU2,DELTA,m,n)
Описание
R = ncfrnd(NU1,NU2,DELTA) функция предназначена для генерации псевдослучайного числа по смещенному F распределению с параметрами NU1,NU2,DELTA. Размерность векторов или матриц параметров NU1,NU2,DELTA должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Размерность R равна размерности векторов или матриц параметров NU1,NU2,DELTA.
R = ncfrnd(NU1,NU2,DELTA,m) позволяет получить вектор или матрицу псевдослучайных чисел на m элементов по смещенному F распределению с параметрами NU1,NU2,DELTA, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = ncfrnd(NU1,NU2,DELTA,m,n) генерирует матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по смещенному F распределению с параметрами NU1,NU2,DELTA.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего заданной паре значений параметров NU1, NU2, DELTA.
>> NU1 =5;
>> NU2=8;
>> DELTA =1;
>> R = ncfrnd(NU1,NU2,DELTA)
R =
1.1032
>> NU1 =[5 6 7 8 9];
>> NU2=8;
>> DELTA =1;
>> R = gamrnd(A,B)
R =
1.6372 0.7624 0.5697 0.4996 2.9616
Генерация вектора псевдослучайных чисел с размерностью 1x4.
>> NU1 =5;
>> NU2=8;
>> DELTA =1;
>> m=[1 4];
>> R = ncfrnd(NU1,NU2,DELTA,m)
R =
2.4729 0.7050 3.5515 0.8951
Второй вариант генерации вектора с размерностью 1x4.
>> NU1 =5;
>> NU2=8;
>> DELTA =1;
>> m=1; n=4;
>> R = ncfrnd(NU1,NU2,DELTA,m,n)
R =
2.3308 1.5732 1.7676 0.3937
Генерация матрицы псевдослучайных чисел с размерностью 4x4.
>> NU1 =5;
>> NU2=8;
>> DELTA =1;
>> m=[4 4];
>> R = ncfrnd(NU1,NU2,DELTA,m)
R =
0.4507 1.3271 1.1275 1.1324
0.2928 1.2401 1.9728 0.9393
0.4897 2.1338 3.4260 0.6466
1.2461 0.7496 0.8716 0.3444
Другой вариант генерации матрицы с размерностью 4x4.
>> NU1 =5;
>> NU2=8;
>> DELTA =1;
>> m=4; n=4;
>> R = ncfrnd(NU1,NU2,DELTA,m,n)
R =
1.4586 0.4415 1.7091 1.0980
1.2270 0.9372 0.4258 0.1006
1.3859 0.2161 0.9851 0.6547
0.2743 1.3568 1.4474 1.1299
Графическая оценка качества генератора псевдослучайных чисел
>> NU1 =5;
>> NU2=8;
>> DELTA =1;
>> R = ncfrnd(NU1,NU2,DELTA,[100 1]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= ncfpdf(X, NU1,NU2,DELTA);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
nctrnd - Смещенное распределение Стьюдента
Синтаксис
R = nctrnd(V,DELTA)
R = nctrnd(V,DELTA,m)
R = nctrnd(V,DELTA,m,n)
Описание
R = nctrnd(V,DELTA) функция предназначена для генерации псевдослучайного числа по смещенному t распределению с параметрами V, DELTA. Размерность векторов или матриц параметров V, DELTA должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Размерность R равна размерности векторов или матриц параметров V, DELTA.
R = nctrnd(V,DELTA,m) позволяет получить вектор псевдослучайных чисел на m элементов по смещенному t распределению с параметрами V, DELTA, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = nctrnd(V,DELTA,m,n) генерирует матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по смещенному t распределению с параметрами V, DELTA.
Примеры использования функции генерации псевдослучайных чисел.
Генерация одного числа соответствующего заданной паре значений параметров V,DELTA.
>> V =10;
>> DELTA =1;
>> R = nctrnd(V,DELTA)
R =
2.0700
>> V =[10 20 30 40 50];
>> DELTA =1;
>> R = nctrnd(V,DELTA)
R =
0.8487 1.6481 1.9022 0.4136 0.7379
Генерация вектора псевдослучайных чисел с размерностью 1x4.
>> V =10;
>> DELTA =1;
>> m=[1 4];
>> R = nctrnd(V,DELTA,m)
R =
2.3386 2.0180 1.4160 0.1664
Второй вариант генерации вектора с размерностью 1x4.
>> V =10;
>> DELTA =1;
>> m=1; n=4;
>> R = nctrnd(V,DELTA,m,n)
R =
0.5278 1.9076 1.5387 0.9368
Генерация матрицы псевдослучайных чисел с размерностью 4x4.
>> V =10;
>> DELTA =1;
>> m=[4 4];
>> R = nctrnd(V,DELTA,m)
R =
2.0307 0.8260 1.8614 0.3730
-1.1576 1.3018 2.3518 0.5920
2.2412 1.9231 0.9035 1.8478
0.7306 3.3665 0.2263 -0.5915
Другой вариант генерации матрицы с размерностью 4x4.
>> V =10;
>> DELTA =1;
>> m=4; n=4;
>> R = nctrnd(V,DELTA,m,n)
R =
0.6733 0.9952 0.6453 2.3441
1.2768 1.2673 0.2516 2.2147
2.1794 1.0644 0.7407 0.9245
0.0379 0.9370 1.0231 0.9637
Графическая оценка качества генератора псевдослучайных чисел
>> V =10;
>> DELTA =1;
>> N=9;
>> R = nctrnd(V,DELTA,[1 1000]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= nctpdf(X, V,DELTA);
>> ff=f*1000*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
normrnd - Нормальное распределение
Синтаксис
R = normrnd(MU,SIGMA)
R = normrnd(MU,SIGMA,m)
R = normrnd(MU,SIGMA,m,n)
Описание
R = normrnd(MU,SIGMA) функция предназначена для генерации псевдослучайного числа по нормальному закону для каждой пары параметров MU (математического ожидания) и SIGMA (среднего квадратического отклонения). Размерность векторов или матриц параметров MU и SIGMA должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Размерность матрицы R равна размерности входных параметров.
R = normrnd(MU,SIGMA,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по нормальному закону для параметров MU и SIGMA, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = normrnd(MU,SIGMA,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по нормальному закону для параметров MU, SIGMA.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего заданной паре значений параметров MU, SIGMA.
>> MU =0;
>> SIGMA =1;
>> R = normrnd(MU,SIGMA)
R =
-0.2953
>> MU =[0 1 2 3];
>> DELTA=[1 2 3 4];
>> R = normrnd(MU,SIGMA)
R =
1.4561 2.8025 0.6664 3.3873
Генерация вектора псевдослучайных чисел с размерностью 1x5.
>> MU =0;
>> SIGMA =1;
>> m=[1 5];
>> R = normrnd(MU,SIGMA,m)
R =
-0.0228 0.1106 0.8128 -1.0091 -1.0046
Второй вариант генерации вектора с размерностью 1x5.
>> MU =0;
>> SIGMA =1;
>> m=1; n=5;
>> R = normrnd(MU,SIGMA,m,n)
R =
0.2830 0.2898 -0.2473 -0.2189 0.8987
Генерация матрицы псевдослучайных чисел с размерностью 4x4.
>> MU =0;
>> SIGMA =1;
>> m=[4 4];
>> R = normrnd(MU,SIGMA,m)
R =
-0.6422 1.5489 -0.5539 -2.5996
-0.1804 -0.0442 0.9324 0.7801
0.7179 -0.0297 -1.3158 0.6029
0.3014 -0.3821 -0.3015 0.9428
Другой вариант генерации матрицы с размерностью 4x4.
>> MU =0;
>> SIGMA =1;
>> m=4; n=4;
>> R = normrnd(MU,SIGMA,m,n)
R =
-1.0239 -1.7813 0.1668 -0.0986
-0.0678 -0.6604 -1.7052 0.1764
0.0818 1.3514 0.2765 -1.8379
-1.7670 2.1364 0.3945 -1.5023
Графическая оценка качества генератора псевдослучайных чисел
>> MU =0;
>> SIGMA =1;
>> N=9;
>> R = normrnd(MU,SIGMA,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= normpdf(X, MU,SIGMA);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
poissrnd - Распределение Пуассона
Синтаксис
R = poissrnd(LAMBDA)
R = poissrnd(LAMBDA,m)
R = poissrnd(LAMBDA,m,n)
Описание
R = poissrnd(LAMBDA) функция предназначена для генерации псевдослучайного числа по распределению Пуассона для каждого значения параметра LAMBDA. Размерность матрицы R равна размерности входного параметра.
R = poissrnd(LAMBDA,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону Пуассона для параметра LAMBDA, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = poissrnd(LAMBDA,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Пуассона для параметра LAMBDA.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра LAMBDA.
>> LAMBDA =0.4;
>> R = poissrnd(LAMBDA)
R =
1
>> LAMBDA =[0.1 0.2 0.3 0.4 0.5];
>> R = poissrnd(LAMBDA)
R =
0 0 1 1 0
Генерация вектора с размерностью 1x5 элементов псевдослучайных чисел.
>> LAMBDA =1;
>> m=[1 5];
>> R = poissrnd(LAMBDA,m)
R =
1 1 3 2 1
Другой вариант генерации вектора с размерностью 1x5.
>> LAMBDA =1;
>> m=1; n=5;
>> R = poissrnd(LAMBDA,m,n)
R =
2 0 0 0 0
Генерация матрицы с размерностью 5x5 элементов.
>> LAMBDA =1;
>> m=[5 5];
>> R = poissrnd(LAMBDA,m)
R =
0 2 2 2 0
0 1 2 1 0
1 3 0 1 1
1 1 2 1 0
1 0 1 0 2
Другой вариант генерации матрицы с размерностью 5x5.
>> LAMBDA =1;
>> m=5; n=5;
>> R = poissrnd(LAMBDA,m,n)
R =
1 0 1 0 3
1 4 0 2 3
2 0 0 0 1
2 0 2 1 1
2 1 0 0 0
Графическая оценка качества генератора псевдослучайных чисел
>> LAMBDA =2;
>> N=9;
>> R = poissrnd(LAMBDA,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):1:max(R);
>> f= poisspdf(X, LAMBDA);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
random - Параметризованная функция генерации псевдослучайных чисел
Синтаксис
y = random('name',A1,A2,A3,m,n)
Описание
y = random('name',A1,A2,A3,m,n) возвращает матрицу случайных чисел согласно заданному распределению. Вид распределения задается значением параметра 'name' в соответствии со следующей таблицей
|
Вид распределения |
Переменная 'name' |
|
Бета |
'beta', 'Beta' |
|
Биномиальное |
'bino', 'Binomial' |
|
Хи-квадрат |
'chi2', 'Chisquare' |
|
Экспоненциальное |
'exp', 'Exponential' |
|
Фишера |
'f', 'F' |
|
Гамма |
'gam', 'Gamma' |
|
Геометрическое |
'geo', 'Geometric' |
|
Гипергеометрическое |
'hyge', 'Hypergeometric' |
|
Логнормальное |
'logn', 'Lognormal' |
|
Отрицательное биномиальное |
'nbin', 'Negative Binomial' |
|
Смещенное Фишера |
'ncf', 'Noncentral F' |
|
Смещенное Стьюдента |
'nct', 'Noncentral T' |
|
Смещенное хи-квадрат |
'ncx2', 'Noncentral Chi-square' |
|
Нормальное |
'norm', 'Normal' |
|
Пуассона |
'poiss', 'Poisson' |
|
Релея |
'rayl', 'Rayleigh' |
|
Стьюдента |
't', 'T' |
|
Дискретное равномерное |
'unid', 'Discrete Uniform' |
|
Непрерывное равномерное |
'unif', 'Uniform' |
|
Вейбулла |
'weib', 'Weibull' |
Параметры A1, A2, A3 являются параметрами перечисленных выше распределений. Последовательность и количество передаваемых параметров A1, A2, A3 должны соответствовать числу и последовательности передаваемым параметрам соответствующих функций генерации псевдослучайных чисел. Размерность векторов или матриц X, A1, A2, A3 должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.
Параметры m и n задают размерность матрицы генерируемых псевдослучайных чисел y. В случае, если параметры распределения A1, A2, A3 заданы как матрицы, то m и n либо могут отсутствовать, либо должны соответствовать размерности указанных переменных.
Примеры использования параметрической функции генерации псевдослучайных чисел
Генерация вектора псевдослучайных чисел распределенных по нормальному закону для вектора значений sigma и определенной величины mu.
>> mu =0;
>> sigma =[1 2 3 4 5];
>> m=1; n=5;
>> y = random('Normal',mu,sigma,m,n)
y =
-1.4228 0.4936 -4.3073 0.5943 -8.4654
Генерация матрицы псевдослучайных чисел по закону Релея для параметра B.
>> B=0.4;
>> m=5; n=5;
>> y = random('Rayleigh',B,m,n)
y =
0.0352 0.5560 0.7423 0.4456 0.1448
0.7218 0.2834 0.2237 0.2255 0.5574
0.1697 0.5745 0.4579 1.0118 0.1382
0.3440 0.6308 0.5983 0.4629 1.0769
0.5596 0.6761 0.4078 0.5654 1.0603
>> R = raylrnd(B)
R =
0.0131 0.0871 0.3479 0.4822 0.6966
raylrnd - Распределение Релея
Синтаксис
R = raylrnd(B)
R = raylrnd(B,m)
R = raylrnd(B,m,n)
Описание
R = raylrnd(B) функция предназначена для генерации псевдослучайного числа по закону Релея для каждого значения параметра B. Размерность матрицы R равна размерности входного параметра.
R = raylrnd(B,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону Релея для параметра B, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = raylrnd(B,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Релея для параметра LAMBDA.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра B.
>> B=0.4;
>> R = raylrnd(B)
R =
0.6883
>> B =[0.1 0.2 0.3 0.4 0.5];
>> R = raylrnd(B)
R =
0.0131 0.0871 0.3479 0.4822 0.6966
Генерация вектора с размерностью 1x5 элементов псевдослучайных чисел.
>> B=0.4;
>> m=[1 5];
>> R = raylrnd(B,m)
R =
0.3374 0.1263 0.6839 0.2867 0.6506
Другой вариант генерации вектора с размерностью 1x5.
>> B=0.4;
>> m=1; n=5;
>> R = raylrnd(B,m,n)
R =
0.3588 0.3786 0.5725 0.7161 0.6429
Генерация матрицы с размерностью 5x5 элементов.
>> B=0.4;
>> m=[5 5];
>> R = raylrnd(B,m)
R =
0.5165 0.1824 0.4208 0.5905 0.2750
0.2674 0.7349 0.3107 0.4149 0.3584
0.4930 0.3100 0.1347 0.2503 0.3540
0.6505 0.4817 0.3985 0.2390 0.5519
0.7496 0.5663 0.8763 0.8898 0.3969
Другой вариант генерации матрицы с размерностью 5x5.
>> B=0.4;
>> m=5; n=5;
>> R = raylrnd(B,m,n)
R =
0.1721 0.4898 0.4207 0.1494 0.2894
0.4838 0.1568 0.3834 0.6791 0.3356
0.5839 0.4527 0.4082 1.0269 0.0930
0.6596 0.5966 0.5196 0.5426 0.5639
0.4335 0.2470 0.3768 0.2075 0.6562
Графическая оценка качества генератора псевдослучайных чисел
>> B=0.4;
>> N=9;
>> R = raylrnd(B,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= raylpdf(X, B);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
trnd - Распределение Стьюдента
Синтаксис
R = trnd(V)
R = trnd(V,m)
R = trnd(V,m,n)
Описание
R = trnd(V) функция предназначена для генерации псевдослучайного числа по распределению Стьюдента для каждого значения числа степеней свободы V. Размерность матрицы R равна размерности входного параметра.
R = trnd(V,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по распределению Стьюдента для параметра V, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = trnd(V,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Пуассона для заданного числа степеней свободы V.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра V.
>> V=10;
>> R = trnd(V)
R =
1.4622
>> V =[10 20 30 40 50];
>> R = trnd(V)
R =
-0.3181 2.1288 0.1322 -2.7310 0.6725
Генерация вектора с размерностью 1x5 элементов псевдослучайных чисел.
>> V=10;
>> m=[1 5];
>> R = trnd(V,m)
R =
0.4941 1.1228 -1.1603 1.5709 -0.6818
Другой вариант генерации вектора с размерностью 1x5.
>> V=10;
>> m=1; n=5;
>> R = trnd(V,m,n)
R =
1.5791 -0.0136 1.0149 0.4422 -1.0674
Генерация матрицы с размерностью 5x5 элементов.
>> V=10;
>> m=[5 5];
>> R = trnd(V,m)
R =
0.7428 1.0015 0.0174 0.8430 -0.1899
2.7214 0.8130 2.6207 -1.6383 -0.9471
2.2282 -2.5067 0.3712 0.6983 -0.6759
0.1904 0.5217 -0.3238 0.6965 2.8145
-1.8868 -1.1012 -0.8685 0.5107 0.1908
Другой вариант генерации матрицы с размерностью 5x5.
>> V=10;
>> m=5; n=5;
>> R = trnd(V,m,n)
R =
1.1892 0.5191 0.6893 1.0224 0.0527
0.8605 1.1526 2.5250 -0.4808 -1.2941
-0.1641 -0.8274 -0.1146 0.0565 -0.1562
0.3315 0.5266 0.2258 0.8991 -0.1739
-0.0379 -0.8681 -1.1669 -2.3567 -0.3615
Графическая оценка качества генератора псевдослучайных чисел
>> V=10;
>> N=9;
>> R = trnd(V,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= tpdf(X, V);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
unidrnd - Дискретное равномерное распределение
Синтаксис
R = unidrnd(N)
R = unidrnd(N,m)
R = unidrnd(N,m,n)
Описание
R = unidrnd(N) функция предназначена для генерации псевдослучайного числа по дискретному равномерному распределению для каждого значения параметра N. Параметр N должен положительным целым числом. Размерность матрицы R равна размерности входного параметра.
R = unidrnd(N,mm) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по дискретному равномерному распределению для параметра N, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = unidrnd(N,mm,nn) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по дискретному равномерному распределению для параметра N.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего определенному значению параметра B.
>> N=10;
>> R = unidrnd(N)
R =
10
>> N =[10 20 30 40 50];
>> R = unidrnd(N)
R =
3 13 15 36 39
Генерация вектора с размерностью 1x5 элементов псевдослучайных чисел.
>> N=10;
>> m=[1 5];
>> R = unidrnd(N,m)
R =
5 1 9 5 7
Другой вариант генерации вектора с размерностью 1x5.
>> N=10;
>> m=1; n=5;
>> R = unidrnd(N,m,n)
R =
8 10 8 2 5
Генерация матрицы с размерностью 5x5 элементов.
>> N=10;
>> m=[5 5];
>> R = unidrnd(N,m)
R =
10 4 2 8 9
10 9 7 5 6
5 1 3 10 3
9 2 2 5 7
1 3 1 5 9
Другой вариант генерации матрицы с размерностью 5x5.
>> N=10;
>> m=5; n=5;
>> R = unidrnd(N,m,n)
R =
1 8 7 4 9
7 5 4 9 9
4 4 6 9 7
9 2 2 6 9
6 2 7 5 7
Графическая оценка качества генератора псевдослучайных чисел
>> N=10;
>> N=9;
>> R = unidrnd(N,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):1:max(R);
>> f= unidpdf(X, N);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
unifrnd - Непрерывное равномерное распределение
Синтаксис
R = unifrnd(A,B)
R = unifrnd(A,B,m)
R = unifrnd(A,B,m,n)
Описание
R = unifrnd(A,B) функция предназначена для генерации псевдослучайного числа по непрерывному равномерному распределению для каждой пары параметров A, B. Размерность векторов или матриц параметров A, B должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Размерность матрицы R равна размерности входных параметров.
R = unifrnd(A,B,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по непрерывному равномерному распределению для параметров A и B, где m - вектор размерностью 1x2 определяющий размерность матрицы R.
R = unifrnd(A,B,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по непрерывному равномерному распределению для параметров A, B.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего заданной паре значений параметров A, B.
>> A=0;
>> B=1;
>> R = unifrnd(A,B)
R =
0.3676
>> A=0;
>> B=[1 2 3 4];
>> R = unifrnd(A,B)
R =
0.6315 1.4353 2.0780 0.3363
Генерация вектора псевдослучайных чисел с размерностью 1x5.
>> A=0;
>> B=1;
>> m=[1 5];
>> R = unifrnd(A,B,m)
R =
0.4544 0.4418 0.3533 0.1536 0.6756
Второй вариант генерации вектора с размерностью 1x5.
>> A=0;
>> B=1;
>> m=1; n=5;
>> R = unifrnd(A,B,m,n)
R =
0.6992 0.7275 0.4784 0.5548 0.1210
Генерация матрицы псевдослучайных чисел с размерностью 4x4.
>> A=0;
>> B=1;
>> m=[4 4];
>> R = unifrnd(A,B,m)
R =
0.4508 0.2548 0.9084 0.0784
0.7159 0.8656 0.2319 0.6408
0.8928 0.2324 0.2393 0.1909
0.2731 0.8049 0.0498 0.8439
Другой вариант генерации матрицы с размерностью 4x4.
>> A=0;
>> B=1;
>> m=4; n=4;
>> R = unifrnd(A,B,m,n)
R =
0.1739 0.3400 0.5915 0.8699
0.1708 0.3142 0.1197 0.9342
0.9943 0.3651 0.0381 0.2644
0.4398 0.3932 0.4586 0.1603
Графическая оценка качества генератора псевдослучайных чисел
>> A=0;
>> B=1;
>> N=9;
>> R = unifrnd(A,B,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= unifpdf(X,A,B);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
weibrnd - Распределение Вейбулла
Синтаксис
R = weibrnd(A,B)
R = weibrnd(A,B,m)
R = weibrnd(A,B,m,n)
Описание
R = weibrnd(A,B) функция предназначена для генерации псевдослучайного числа по закону Вейбулла для каждой пары параметров A, B. Размерность векторов или матриц параметров A, B должна быть одинаковой. Скалярный параметр увеличивается до размера остальных входных аргументов. Размерность матрицы R равна размерности входных параметров.
R = weibrnd(A,B,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону Вейбулла для параметров A и B, где m - вектор размерностью 1x2 определяющий размерность матрицы R. R = weibrnd(A,B,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Вейбулла для параметров A и B.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного числа соответствующего заданной паре значений параметров A, B.
>> A=1;
>> B=2;
>> R = weibrnd (A,B)
R =
1.5743
>> A=1;
>> B=[1 2 3 4];
>> R = weibrnd (A,B)
R =
0.0561 0.2963 0.7977 1.0823
Генерация вектора псевдослучайных чисел с размерностью 1x5.
>> A=1;
>> B=2;
>> m=[1 5];
>> R = weibrnd (A,B,m)
R =
0.3678 0.8165 0.5578 0.9286 0.1985
Второй вариант генерации вектора с размерностью 1x5.
>> A=1;
>> B=2;
>> m=1; n=5;
>> R = weibrnd (A,B,m,n)
R =
1.6218 0.7692 1.1095 0.3914 1.0447
Генерация матрицы псевдослучайных чисел с размерностью 4x4.
>> A=1;
>> B=2;
>> m=[4 4];
>> R = weibrnd (A,B,m)
R =
0.6208 0.9131 0.3276 0.6328
1.7115 0.7586 0.5307 1.2669
1.0154 0.6953 0.4840 1.1393
0.8346 1.4756 0.4524 0.6841
Другой вариант генерации матрицы с размерностью 4x4.
>> A=1;
>> B=2;
>> m=4; n=4;
>> R = weibrnd (A,B,m,n)
R =
0.7887 0.9454 1.0544 0.4324
1.6798 0.8640 0.8589 0.2118
1.5555 0.3089 0.7180 0.7199
1.1421 0.7191 1.3504 1.8839
Графическая оценка качества генератора псевдослучайных чисел
>> A=1;
>> B=2;
>> N=9;
>> R = weibrnd (A,B,[1 100]);
>> hist(R, N)
>> grid on
>> X=min(R):(max(R)-min(R))/100:max(R);
>> f= weibpdf(X,A,B);
>> ff=f*100*((max(R)-min(R))/N);
>> hold on
>> plot(X,ff,'r')
>> hold off
wishrnd - Матрица случайных чисел распределения Уишарта
Синтаксис
W = wishrnd(SIGMA,df)
W = wishrnd(SIGMA,df,D)
[W,D] = wishrnd(SIGMA,df)
Описание
W = wishrnd(SIGMA,df) служит для генерации матицы случайных чисел распределенных по распределению Уишарта для ковариационной матрицы SIGMA с числом степеней свободы df.
W = wishrnd(SIGMA,df,D) в отличии от предыдущего варианта синтаксиса задается коэффициент Холецкого D ковариационной матрицы SIGMA. В случае нескольких вызовов функции wishrnd с одинаковыми значениями ковариационной матрицы для увеличения эффективности алгоритма генерации целесообразно явно задавать коэффициент Холецкого D.
[W,D] = wishrnd(SIGMA,df) в отличии от первого варианта вызова функции кроме матрицы псевдослучайных чисел W возвращается значение коэффициента Холецкого DI, который может быть использован при последующих вызовах функции wishrnd.
Примеры использования функции генерации псевдослучайных чисел
Генерация псевдослучайных чисел по распределению Уишарта.
>> SIGMA=pascal(3)
SIGMA =
1 1 1
1 2 3
1 3 6
>> df=5
df =
5
>> W=wishrnd(SIGMA,df)
W =
4.3741 1.7676 -1.2564
1.7676 2.1324 3.4334
-1.2564 3.4334 16.1057
Генерация псевдослучайных чисел по распределению Уишарта и расчет коэффициента Холецкого DI.
>> SIGMA=pascal(3)
SIGMA =
1 1 1
1 2 3
1 3 6
>> df=5
df =
5
>> [W,DI]=wishrnd(SIGMA,df)
W =
3.4728 2.8301 2.1133
2.8301 5.5233 8.7450
2.1133 8.7450 22.9138
DI =
1 1 1
0 1 2
0 0 1
Расчет псевдослучайных чисел согласно распределению Уишарта и использование
коэффициента Холецкого DI при повторной генерации.
>> SIGMA=pascal(5)
SIGMA =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
>> df=10
df =
10
>> [W,DI]=wishrnd(SIGMA,df)
W =
10.7636 8.9244 4.7621 -6.4387 -32.4934
8.9244 13.6604 14.7491 10.0681 -4.8925
4.7621 14.7491 24.6901 34.7112 42.2157
-6.4387 10.0681 34.7112 74.8364 135.2491
-32.4934 4.8925 42.2157 135.2491 304.2332
DI =
1 1 1 1 1
0 1 2 3 4
0 0 1 3 6
0 0 0 1 4
0 0 0 0 1
>> W=wishrnd(SIGMA,df,DI)
W =
10.1921 15.0520 15.6658 9.8037 -2.7973
15.0520 28.1868 36.0149 32.3553 18.0655
15.6658 36.0149 56.1620 66.3571 67.0877
9.8037 32.3553 66.3571 106.9305 157.7394
-2.7973 18.0655 67.0877 157.7394 311.6346
betastat - Бета распределение
Синтаксис
[M,V] = betastat(A,B)
Описание
[M,V] = betastat(A,B) функция служит для расчета математического ожидания и дисперсии бета распределения с заданными параметрами A и B. Размерность векторов и матриц A и B должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M бета распределения с заданными параметрами A и B определяется по формуле
![]()
Дисперсия V бета распределения с заданными параметрами A и B определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии бета распределения для пары параметров А и В.
>> A=1
A =
1
>> B=2
B =
2
>> [M,V] = betastat(A,B)
M =
0.3333
V =
0.0556
Расчет математического ожидания и дисперсии бета распределения для матриц параметров А и В.
>> A=[1 2 3; 4 5 6]
A =
1 2 3
4 5 6
>> B=[2 3 4; 5 6 7]
B =
2 3 4
5 6 7
>> [M,V] = betastat(A,B)
M =
0.3333 0.4000 0.4286
0.4444 0.4545 0.4615
V =
0.0556 0.0400 0.0306
0.0247 0.0207 0.0178
Расположение математического ожидания M и интервалов [M-![]() ; M+?], [M-2
; M+?], [M-2![]() ; M+2
; M+2![]() ], [M-3
], [M-3![]() ; M+3
; M+3![]() ]
]
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> A= 2;
>> B= 2;
>> X= -0.2:0.01:1.1;
>> Y= betapdf(X,A,B);
>> plot(X,Y)
>> grid on
>> [M,V] = betastat(A,B)
M =
0.5000
V =
0.0500
>> sigma=sqrt(V)
sigma =
0.2236
>> H1=line ([M-3*sigma M-3*sigma], [0 betapdf((M-3*sigma),A,B)+0.1]);
>> set(H1,'Color','m')
>> H2=line ([M-2*sigma M-2*sigma], [0 betapdf((M-2*sigma),A,B)+0.1]);
>> set(H2,'Color','g')
>> H3=line ([M-sigma M-sigma], [0 betapdf((M-sigma),A,B)+0.1]);
>> set(H3,'Color','c')
>> H4=line ([M M], [0 betapdf((M),A,B)+0.1]);
>> set(H4,'LineWidth',3, 'Color','k')
>> H5=line ([M+sigma M+sigma], [0 betapdf((M+sigma),A,B)+0.1]);
>> set(H5,'Color','c')
>> H6=line ([M+2*sigma M+2*sigma], [0 betapdf((M+2*sigma),A,B)+0.1]);
>> set(H6,'Color','g')
>> H7=line ([M+3*sigma M+3*sigma], [0 betapdf((M+3*sigma),A,B)+0.1]);
>> set(H7,'Color','m')
binostat - Биномиальное распределение
Синтаксис
[M,V] = binostat(N,P)
Описание
[M,V] = binostat(N,P) функция служит для расчета математического ожидания и дисперсии биномиального распределения с заданными параметрами N и P. Размерность векторов и матриц N и P должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M биномиального распределения с заданными параметрами N и P определяется по формуле
![]()
Дисперсия V биномиального распределения с заданными параметрами N и P определяется по формуле
![]()
где P - вероятность появления события в одном испытании, Q - вероятность обратного события в одном опыте, Q=1-P.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии биномиального распределения для пары параметров N и P.
>> N=10
N =
10
>> P=0.2
P =
0.2
>> [M,V] = binostat(N,P)
M =
2
V =
1.6000
Расчет математического ожидания и дисперсии биномиального распределения для матриц параметров N и P.
>> N=[10 20 30; 40 50 60]
N =
10 20 30
40 50 60
>> P=[0.2 0.3 0.4; 0.5 0.6 0.7]
P =
0.2000 0.3000 0.4000
0.5000 0.6000 0.7000
>> [M,V] = binostat(N,P)
M =
2 6 12
20 30 42
V =
1.6000 4.2000 7.2000
10.0000 12.0000 12.6000
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ], [M-3
], [M-3![]() ; M+3
; M+3![]() ]
]
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> N=50;
>> P=0.2;
>> X= 0:1:30;
>> Y= binopdf(X,N,P);
>> plot(X,Y)
>> grid on
>> [M,V] = binostat(N,P)
M =
10
V =
8
>> sigma=sqrt(V)
sigma =
2.8284
>> H1=line ([M-3*sigma M-3*sigma], [0 binopdf(floor(M-3*sigma),N,P)+0.01]);
>> set(H1,'Color','m')
>> H2=line ([M-2*sigma M-2*sigma], [0 binopdf(floor(M-2*sigma),N,P)+0.01]);
>> set(H2,'Color','g')
>> H3=line ([M-sigma M-sigma], [0 binopdf(floor(M-sigma),N,P)+0.01]);
>> set(H3,'Color','c')
>> H4=line ([M M], [0 binopdf(M,N,P)+0.01]);
>> set(H4,'LineWidth',2, 'Color','k')
>> H5= line ([M+sigma M+sigma], [0 binopdf(floor(M+sigma),N,P)+0.01]);
>> set(H5,'Color','c')
>> H6=line ([M+2*sigma M+2*sigma], [0 binopdf(floor(M+2*sigma),N,P)+0.01]);
>> set(H6,'Color','g')
>> H7=line ([M+3*sigma M+3*sigma], [0 binopdf(floor(M+3*sigma),N,P)+0.01]);
>> set(H7,'Color','m')
chi2stat - Функция распределения хи-квадрат
Синтаксис:
[M,V] = chi2stat(NU)
Описание :
[M,V] = chi2stat(NU) функция служит для расчета математического ожидания и дисперсии распределения хи-квадрат с заданным числом степеней свободы NU.
Математическое ожидание распределения хи-квадрат равно M=NU. Дисперсия определяется как V=2*NU
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии распределения хи-квадрат для параметра NU.
>> NU=10
NU =
10
>> [M,V] = chi2stat(NU)
M =
10
V =
20
Расчет математического ожидания и дисперсии распределения хи-квадрат для матрицы параметра NU.
>> NU=[10 20 30; 40 50 60]
NU =
10 20 30
40 50 60
>> [M,V] = chi2stat(NU)
M =
10 20 30
40 50 60
V =
20 40 60
80 100 120
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ],
],
[M-3![]() ; M+3
; M+3![]() ] на графике функции плотности вероятности,
] на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> NU=10;
>> X= 0:0.01:30;
>> Y= chi2pdf(X,NU);
>> plot(X,Y)
>> grid on
>> [M,V] = chi2stat(NU)
M =
10
V =
20
>> sigma=sqrt(V)
sigma =
4.4721
>> H=line ([M M], [0 chi2pdf(M,NU)+0.01]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 chi2pdf(M-sigma,NU)+0.01]);
>> set(H1,'Color','c')
>> H2=line ([M+sigma M+sigma], [0 chi2pdf(M+sigma,NU)+0.01]);
>> set(H2,'Color','c')
>> H3=line ([M-2*sigma M-2*sigma], [0 chi2pdf(M-2*sigma,NU)+0.01]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 chi2pdf(M+2*sigma,NU)+0.01]);
>> set(H4,'Color','m')
>> H5=line ([M-3*sigma M-3*sigma], [0 chi2pdf(M-3*sigma,NU)+0.01]);
>> set(H5,'Color','g')
>> H6=line ([M+3*sigma M+3*sigma], [0 chi2pdf(M+3*sigma,NU)+0.01]);
>> set(H6,'Color','g')
expstat - Экспоненциальное распределение
Синтаксис:
[M,V] = expstat(MU)
Описание:
[M,V] = expstat(MU) функция служит для расчета математического ожидания и дисперсии экспоненциального распределения с заданным параметром MU.
Математическое ожидание экспоненциального распределения равно M=MU. Дисперсия определяется как V=MU2.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии экспоненциального распределения для параметра MU.
>> MU=1 MU = 1 >> [M,V] = expstat(MU) M = 1 V = 1 Расчет математического ожидания и дисперсии экспоненциального распределения для матрицы параметра MU. >> MU=[1 2 3; 4 5 6] N = 10 20 30 40 50 60 >> [M,V] = expstat(MU) M = 1 2 3 4 5 6 V = 1 4 9 16 25 36 Расположение математического ожидания M и значений (M-); (M+
); (M+2
); (M+3
) на графике функции плотности вероятности,
- среднее квадратическое отклонение. >> MU=10; >> X= 0:0.01:30; >> Y= exppdf(X,MU); >> plot(X,Y) >> grid on >> [M,V] = expstat(MU) M = 10 V = 100 >> sigma=sqrt(V) sigma = 10 >> H=line ([M M], [0 exppdf(M,MU)+0.01]); >> set(H,'LineWidth',3, 'Color','k') >> H1=line ([M-sigma M-sigma], [0 exppdf(M-sigma,MU)+0.01]); >> set(H1,'Color','c') >> H2=line ([M+sigma M+sigma], [0 exppdf(M+sigma,MU)+0.01]); >> set(H2,'Color','c') >> H3=line ([M+2*sigma M+2*sigma], [0 exppdf(M+2*sigma,MU)+0.01]); >> set(H3,'Color','m') >> H4=line ([M+3*sigma M+3*sigma], [0 exppdf(M+3*sigma,MU)+0.01]); >> set(H4,'Color','g')

fstat - Распределение Фишера
Синтаксис:
[M,V] = fstat(V1,V2)
Описание:
[M,V] = fstat(V1,V2) функция служит для расчета математического ожидания и дисперсии F распределения с заданными параметрами V1 и V2. Размерность векторов и матриц V1 и V2 должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание F распределения с заданными параметрами V1 и V2 определяется по формуле
![]()
Дисперсия F распределения с заданными параметрами V1 и V2 определяется по формуле
![]()
Математическое ожидание F распределения не существует при V2<3. Дисперсия не определена при V2<5.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии F распределения для пары параметров V1 и V2.
>> V1=10
V1 =
10
>> V2=20
V2 =
2
>> [M,V] = fstat(V1,V2)
M =
1.1111
V =
0.4321
Расчет математического ожидания и дисперсии F распределения для матриц параметров V1 и V2.
>> V1=[1 2 3; 4 5 6]
V1 =
1 2 3
4 5 6
>> V2=[2 3 4; 5 6 7]
V2 =
2 3 4
5 6 7
>> [M,V] = fstat(V1,V2)
M =
NaN 3.0000 2.0000
1.6667 1.5000 1.4000
V =
NaN NaN NaN
9.7222 4.0500 2.3956
Расположение математического ожидания M и значений (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() )
)
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> V1= 5;
>> V2= 8;
>> X= 0:0.01:8;
>> Y= fpdf(X,V1,V2);
>> plot(X,Y)
>> grid on
>> [M,V] = fstat(V1,V2)
M =
1.3333
V =
1.9556
>> sigma=sqrt(V)
sigma =
1.3984
>> H1=line ([M-sigma M-sigma], [0 fpdf((M-sigma), V1,V2)+0.1]);
>> set(H1,'Color','c')
>> H2=line ([M M], [0 fpdf((M),V1,V2)+0.1]);
>> set(H2,'LineWidth',3, 'Color','k')
>> H3=line ([M+sigma M+sigma], [0 fpdf((M+sigma),V1,V2)+0.1]);
>> set(H3,'Color','c')
>> H4=line ([M+2*sigma M+2*sigma], [0 fpdf((M+2*sigma),V1,V2)+0.1]);
>> set(H4,'Color','g')
>> H5=line ([M+3*sigma M+3*sigma], [0 fpdf((M+3*sigma),V1,V2)+0.1]);
>> set(H5,'Color','m')
gamstat - Гамма распределение
Синтаксис
[M,V] = gamstat(A,B)
Описание
[M,V] = gamstat(A,B) функция служит для расчета математического ожидания и дисперсии Гамма распределения с заданными параметрами A и B. Размерность векторов и матриц A и B должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание Гамма распределения с заданными параметрами A и B определяется по формуле
![]()
Дисперсия Гамма распределения с заданными параметрами A и B определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии Гамма распределения для пары параметров А и В.
>> A=1
A =
1
>> B=2
B =
2
>> [M,V] = gamstat(A,B)
M =
2
V =
4
Расчет математического ожидания и дисперсии Гамма распределения для матриц параметров А и В.
>> A=[1 2 3; 4 5 6]
A =
1 2 3
4 5 6
>> B=[2 3 4; 5 6 7]
B =
2 3 4
5 6 7
>> [M,V] = gamstat(A,B)
M =
2 6 12
20 30 42
V =
4 18 48
100 180 294
Расположение математического ожидания M и значений (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() )
)
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> A= 1;
>> B= 2;
>> X= -0.1:0.01:10;
>> Y= gampdf(X,A,B);
>> plot(X,Y)
>> grid on
>> [M,V] = gamstat(A,B)
M =
2
V =
4
>> sigma=sqrt(V)
sigma =
2
>> H=line ([M M], [0 gampdf((M),A,B)+0.1]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 gampdf((M-sigma),A,B)+0.1]);
>> set(H1,'Color','c')
>> H2=line ([M+sigma M+sigma], [0 gampdf((M+sigma),A,B)+0.1]);
>> set(H2,'Color','c')
>> H3=line ([M+2*sigma M+2*sigma], [0 gampdf((M+2*sigma),A,B)+0.1]);
>> set(H3,'Color','g')
>> H4=line ([M+3*sigma M+3*sigma], [0 gampdf((M+3*sigma),A,B)+0.1]);
>> set(H4,'Color','m')
geostat - Геометрическое распределение
Синтаксис
[M,V] = geostat(P)
Описание
[M,V] = geostat(P) функция служит для расчета математического ожидания и дисперсии геометрического распределения с заданным параметром P. Размерность векторов или матриц M и V совпадает размерностью входного параметра.
Математическое ожидание геометрического распределения равно ![]() . Дисперсия определяется как
. Дисперсия определяется как ![]() .
.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии геометрического распределения для параметра P.
>> P=0.1
P =
0.1
>> [M,V] = geostat(P)
M =
9
V =
90
Расчет математического ожидания и дисперсии геометрического распределения для матрицы параметра P.
>> P=[0.1 0.2 0.3; 0.4 0.5 0.6]
P =
0.1000 0.2000 0.3000
0.4000 0.5000 0.6000
>> [M,V] = geostat(P)
M =
9.0000 4.0000 2.3333
1.5000 1.0000 0.6667
V =
90.0000 20.0000 7.7778
3.7500 2.0000 1.1111
Расположение математического ожидания M и значений (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() )
)
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> P=0.1;
>> X= 0:1:40;
>> Y= geopdf(X,P);
>> plot(X,Y)
>> grid on
>> [M,V] = geostat(P)
M =
9
V =
90
>> sigma=sqrt(V)
sigma =
9.4868
>> H=line ([M M], [0 geopdf(M,P)+0.01]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 geopdf(floor(M-sigma),P)+0.01]);
>> set(H1,'Color','c')
>> H2=line ([M+sigma M+sigma], [0 geopdf(floor(M+sigma),P)+0.01]);
>> set(H2,'Color','c')
>> H3=line ([M+2*sigma M+2*sigma], [0 geopdf(floor(M+2*sigma),P)+0.01]);
>> set(H3,'Color','m')
>> H4=line ([M+3*sigma M+3*sigma], [0 geopdf(floor(M+3*sigma),NU)+0.01]);
>> set(H4,'Color','g')
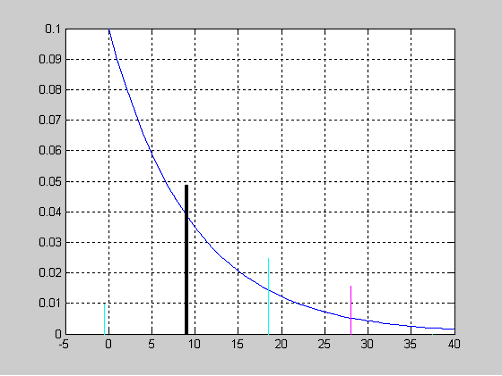
hygestat - Гипергеометрическое распределение
Синтаксис
[M,V] = hygestat(M,K,N)
Описание
[M,V] = hygestat(M,K,N) функция служит для расчета математического ожидания и дисперсии гипергеометрического распределения с заданными параметрами M, K и N. Размерность векторов и матриц M, K и N должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью остальных параметров. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание гипергеометрического распределения с заданными параметрами M, K и N определяется по формуле
![]()
Дисперсия гипергеометрического распределения с заданными параметрами M, K и N определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии гипергеометрического распределения для сочетания значений параметров M, K ,N.
>> M=10
M =
10
>> N=5
N =
5
>> K=3
K =
3
>> [M,V] = hygestat(M,K,N)
M =
1.5000
V =
0.5833
Расчет математического ожидания и дисперсии гипергеометрического распределения для матриц параметров M, K ,N.
>> M=[20 30; 40 50]
M =
20 30
40 50
>> N=[10 20; 30 40]
N =
10 20
30 40
>> K=[3 5; 7 9]
K =
3 5
7 9
>> [M,V] = hygestat(M,K,N)
M =
1.5000 3.3333
5.2500 7.2000
V =
0.6711 0.9579
1.1106 1.2049
Расположение математического ожидания M и значений (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() )
)
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> M=100;
>> N=50;
>> K=40;
>> X=0:1:40;
>> Y= hygepdf(X,M,K,N);
>> plot(X,Y)
>> grid on
>> [Mx,V] = hygestat(M,K,N)
Mx=
20
V =
6.0606
>> sigma=sqrt(V)
sigma =
2.4618
>> H=line ([Mx Mx], [0 hygepdf(Mx,M,K,N)+0.01]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([Mx-sigma Mx-sigma], [0 hygepdf(floor(Mx-sigma),M,K,N)+0.01]);
>> set(H1,'Color','c')
>> H2=line ([Mx+sigma Mx+sigma], [0 hygepdf(floor(Mx+sigma),M,K,N)+0.01]);
>> set(H2,'Color','c')
>> H3=line ([Mx+2*sigma Mx+2*sigma], [0 hygepdf(floor(Mx+2*sigma),M,K,N)+0.01]);
>> set(H3,'Color','m')
>> H4=line([Mx+3*sigma Mx+3*sigma], [0 hygepdf(floor(Mx+3*sigma),M,K,N)+0.01]);
>> set(H4,'Color','g')
>> H5=line ([Mx-2*sigma Mx-2*sigma], [0 hygepdf(floor(Mx-2*sigma),M,K,N)+0.01]);
>> set(H5,'Color','m')
>> H6=line([Mx-3*sigma Mx-3*sigma], [0 hygepdf(floor(Mx-3*sigma),M,K,N)+0.01]);
>> set(H6,'Color','g')
lognstat - Логнормальное распределение
Синтаксис
[M,V] = lognstat(MU,SIGMA)
Описание
[M,V] = lognstat(MU,SIGMA) функция служит для расчета математического ожидания и дисперсии логнормального распределения с заданными параметрами MU и SIGMA. Размерность векторов и матриц MU и SIGMA должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание логнормального распределения с заданными параметрами MU и SIGMA определяется по формуле
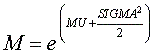
Дисперсия логнормального распределения с заданными параметрами MU и SIGMA определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии логнормального распределения для пары параметров MU и SIGMA.
>> MU=0
MU =
0
>> SIGMA =1
SIGMA =
1
>> [M,V] = lognstat(MU,SIGMA)
M =
1.6487
V =
4.6708
Расчет математического ожидания и дисперсии логнормального распределения для матриц параметров MU и SIGMA.
>> MU =[1 2 3; 4 5 6]
MU =
1 2 3
4 5 6
>> SIGMA=[2 3 4; 5 6 7]
SIGMA =
2 3 4
5 6 7
>> [M,V] = lognstat(MU,SIGMA)
M =
1.0e+013 *
0.0000 0.0000 0.0000
0.0000 0.0010 1.7619
V =
1.0e+047 *
0.0000 0.0000 0.0000
0.0000 0.0000 5.9210
Расположение математического ожидания M и значений (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() )
)
на графике функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> MU=0;
>> SIGMA =1;
>> X= 0:0.01:8;
>> Y= lognpdf(X, MU, SIGMA);
>> plot(X,Y)
>> grid on
>> [M,V] = lognstat(MU,SIGMA)
M =
1.6487
V =
4.6708
>> s=sqrt(V)
s =
2.1612
>> H1=line ([M-s M-s], [0 0.1]);
>> set(H1,'Color','c')
>> H2=line([M M], [0 lognpdf(M,MU,SIGMA)+0.1]);
>> set(H2,'LineWidth',3, 'Color','k')
>> H3= line ([M+s M+s], [0 lognpdf(M+s,MU,SIGMA)+0.1]);
>> set(H3,'Color','c')
>> H4= line ([M+2*s M+2*s], [0 lognpdf(M+2*s,MU,SIGMA)+0.1]);
>> set(H4,'Color','g')
>> H5= line ([M+3*s M+3*s], [0 lognpdf(M+3*s,MU,SIGMA)+0.1]);
>> set(H5,'Color','m')
nbinstat - Отрицательное биномиальное распределение
Синтаксис
[M,V] = nbinstat(R,P)
Описание
[M,V] = nbinstat(R,P) функция служит для расчета математического ожидания и дисперсии отрицательного биномиального распределения с заданными параметрами R и P. Размерность векторов и матриц R и P должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M отрицательного биномиального распределения с заданными параметрами R и P определяется по формуле
![]()
где P - вероятность появления события в одном испытании, Q - вероятность обратного события в одном опыте, Q=1-P.
Дисперсия V отрицательного биномиального распределения с заданными параметрами R и P определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии отрицательного биномиального распределения для пары параметров R и P.
>> R=1
R =
1
>> P=0.2
P =
0.2000
>> [M,V] = nbinstat(R,P)
M =
4
V =
20.0000
Расчет математического ожидания и дисперсии отрицательного биномиального распределения для матриц параметров R и P.
>> R=[1 2 3; 4 5 6]
R =
1 2 3
4 5 6
>> P=[0.2 0.3 0.4; 0.5 0.6 0.7]
P =
0.2000 0.3000 0.4000
0.5000 0.6000 0.7000
>> [M,V] = nbinstat(R,P)
M =
4.0000 4.6667 4.5000
4.0000 3.3333 2.5714
V =
20.0000 15.5556 11.2500
8.0000 5.5556 3.6735
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ], [M-3
], [M-3![]() ; M+3
; M+3![]() ] на графике функции
] на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> R=10;
>> P=0.5;
>> X= 0:1:30;
>> Y= nbinpdf(X,R,P);
>> plot(X,Y)
>> grid on
>> [M,V] = nbinstat(R,P)
M =
10
V =
20
>> sigma=sqrt(V)
sigma =
4.4721
>> H1=line ([M-3*sigma M-3*sigma], [0 nbinpdf(floor(M-3*sigma),R,P)+0.01]);
>> set(H1,'Color','m')
>> H2=line ([M-2*sigma M-2*sigma], [0 nbinpdf(floor(M-2*sigma),R,P)+0.01]);
>> set(H2,'Color','g')
>> H3=line ([M-sigma M-sigma], [0 nbinpdf(floor(M-sigma),R,P)+0.01]);
>> set(H3,'Color','c')
>> H4=line ([M M], [0 nbinpdf(M,R,P)+0.01]);
>> set(H4,'LineWidth',2, 'Color','k')
>> H5= line ([M+sigma M+sigma], [0 nbinpdf(floor(M+sigma),R,P)+0.01]);
>> set(H5,'Color','c')
>> H6=line ([M+2*sigma M+2*sigma], [0 nbinpdf(floor(M+2*sigma),R,P)+0.01]);
>> set(H6,'Color','g')
>> H7=line ([M+3*sigma M+3*sigma], [0 nbinpdf(floor(M+3*sigma),R,P)+0.01]);
>> set(H7,'Color','m')
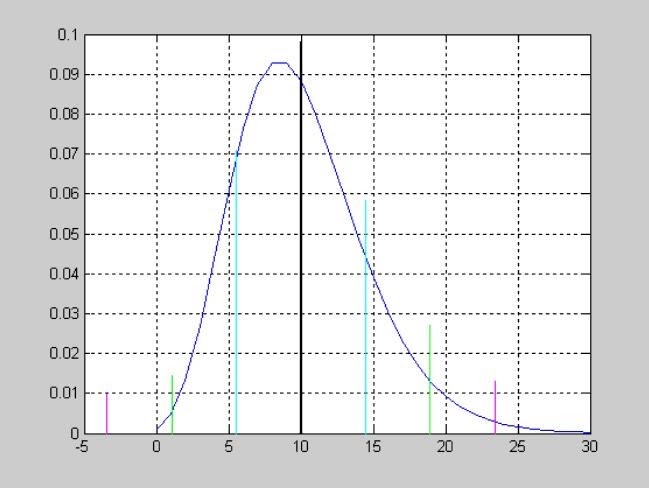
ncfstat - Смещенное распределение Фишера
Синтаксис
[M,V] = ncfstat(NU1,NU2,DELTA)
Описание
[M,V] = ncfstat(NU1,NU2,DELTA) функция служит для расчета математического ожидания и дисперсии смещенного F распределения с заданными параметрами NU1, NU2 и DELTA. Размерность векторов и матриц NU1, NU2 и DELTA должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью остальных параметров. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание смещенного F распределения с заданными параметрами NU1, NU2 и DELTA определяется по формуле
Дисперсия смещенного F распределения с заданными параметрами NU1, NU2 и DELTA определяется по формуле
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии смещенного F распределения для сочетания значений параметров NU1, NU2 и DELTA.
>> NU1=8
NU1 =
8
>> NU2=5
NU2 =
5
>> DELTA =1
DELTA =
1
>> [M,V] = ncfstat(NU1,NU2,DELTA)
M =
1.8750
V =
9.6354
Расчет математического ожидания и дисперсии смещенного F распределения для матриц параметров NU1, NU2 и DELTA.
>> NU1=[20 30; 40 50]
NU1 =
20 30
40 50
>> NU2=[10 20; 30 40]
NU2 =
10 20
30 40
>> DELTA=[3 5; 7 9]
DELTA =
3 5
7 9
>> [M,V] = ncfstat(NU1,NU2,DELTA)
M =
1.4375 1.2963
1.2589 1.2421
V =
0.9596 0.3335
0.2054 0.1493
Расположение математического ожидания M и значений (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() ) на графике
) на графике
функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> DELTA=5;
>> NU1=10;
>> NU2=20;
>> X= 0:0.01:6;
>> Y= ncfpdf(X,NU1,NU2,DELTA);
>> plot(X,Y)
>> grid on
>>[M,V] = ncfstat(NU1,NU2,DELTA)
M =
1.6667
V =
0.9028
>> sigma=sqrt(V)
sigma =
0.9501
>> H1=line ([M-sigma M-sigma], [0 ncfpdf((M-sigma),NU1,NU2,DELTA)+0.1]);
>> set(H1,'Color','c')
>> H2=line ([M M], [0 ncfpdf((M),NU1,NU2,DELTA)+0.1]);
>> set(H2,'LineWidth',3, 'Color','k')
>> H3=line ([M+sigma M+sigma], [0 ncfpdf((M+sigma),NU1,NU2,DELTA)+0.1]);
>> set(H3,'Color','c')
>> H4=line ([M+2*sigma M+2*sigma], [0 ncfpdf((M+2*sigma),NU1,NU2,DELTA)+0.1]);
>> set(H4,'Color','g')
>> H5=line ([M+3*sigma M+3*sigma], [0 ncfpdf((M+3*sigma),NU1,NU2,DELTA)+0.1]);
>> set(H5,'Color','m')
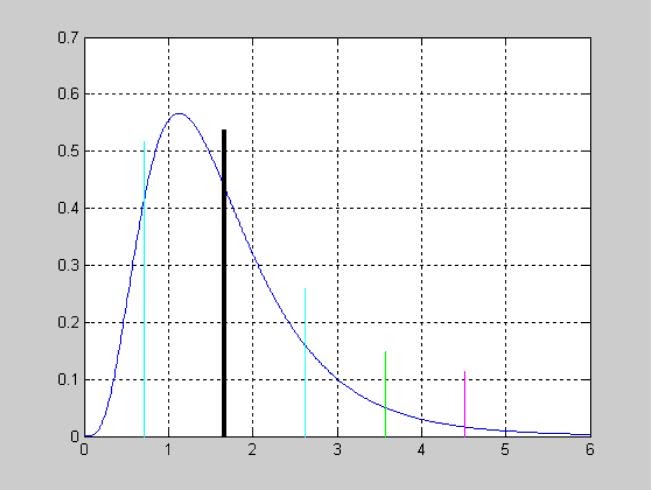
nctstat - Смещенное распределение Стьюдента
Синтаксис
[M,V] = nctstat(NU,DELTA)
Описание
[M,V] = nctstat(NU,DELTA) функция служит для расчета математического ожидания и дисперсии смещенного t распределения с заданными параметрами числа степеней свободы NU и параметра смещения DELTA. Размерность векторов и матриц NU, DELTA должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M смещенного t распределения с заданными параметрами NU и DELTA определяется по формуле
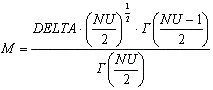
при условии, что число степеней свободы NU>1.
Дисперсия V смещенного t распределения с заданными параметрами NU и DELTA определяется по формуле
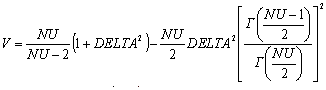
при условии, что число степеней свободы NU>2.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии смещенного t распределения для сочетания значений параметров NU, DELTA.
>> NU=8
NU =
8
>> DELTA =1
DELTA =
1
>>[M,V] = nctstat(NU,DELTA)
M =
1.1078
V =
1.4395
Расчет математического ожидания и дисперсии смещенного t распределения для матриц параметров NU, DELTA.
>> NU=[10 20; 30 40]
NU =
10 20
30 40
>> DELTA=[3 5; 7 9]
DELTA =
3 5
7 9
>>[M,V] = nctstat(NU,DELTA)
M =
3.2512 5.1978
7.1813 9.1733
V =
1.9299 1.8717
2.0004 2.1670
Расположение математического ожидания M и значений (M-3![]() ); (M-2
); (M-2![]() ); (M-
); (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() ) на графике функции
) на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> DELTA=5;
>> NU=10;
>> X=1:0.01:15;
>> Y= nctpdf(X,NU,DELTA);
>> plot(X,Y)
>> grid on
>>[M,V] = nctstat(NU,DELTA)
M =
5.4186
V =
3.1386
>> sigma=sqrt(V)
sigma =
1.7716
>> H1=line ([M-3*sigma M-3*sigma], [0 nctpdf((M-3*sigma),NU,DELTA)+0.02]);
>> set(H1,'Color','m')
>> H2=line ([M-2*sigma M-2*sigma], [0 nctpdf((M-2*sigma),NU,DELTA)+ 0.02]);
>> set(H2,'Color','g')
>> H3=line ([M-sigma M-sigma], [0 nctpdf((M-sigma),NU,DELTA)+0.02]);
>> set(H3,'Color','c')
>> H4=line ([M M], [0 nctpdf((M),NU,DELTA)+0.02]);
>> set(H4,'LineWidth',3, 'Color','k')
>> H5=line ([M+sigma M+sigma], [0 nctpdf((M+sigma),NU,DELTA)+0.02]);
>> set(H5,'Color','c')
>> H6=line ([M+2*sigma M+2*sigma], [0 nctpdf((M+2*sigma),NU,DELTA)+0.02]);
>> set(H6,'Color','g')
>> H7=line ([M+3*sigma M+3*sigma], [0 nctpdf((M+3*sigma),NU,DELTA)+0.02]);
>> set(H7,'Color','m')
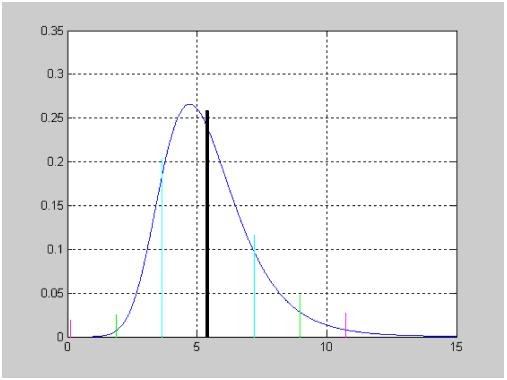
ncx2stat - математического ожидания и дисперсии смещенного хи-квадрат распределения по заданным параметрам
Синтаксис
[M,V] = ncx2stat(NU,DELTA)
Описание
[M,V] = ncx2stat(NU,DELTA) функция служит для расчета математического ожидания и дисперсии смещенного хи-квадрат распределения с заданными параметрами числа степеней свободы NU и параметра смещения DELTA. Размерность векторов и матриц NU, DELTA должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M смещенного хи-квадрат распределения с заданными параметрами NU и DELTA определяется по формуле
M=DELTA+NU
Дисперсия V смещенного хи-квадрат распределения с заданными параметрами NU и DELTA определяется по формуле
V=2*(NU+2*DELTA)2
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии смещенного хи-квадрат распределения для сочетания значений
параметров NU, DELTA.
>> NU=5
NU =
5
>> DELTA =2
DELTA =
2
>>[M,V] = ncx2stat (NU,DELTA)
M =
7
V =
18
Расчет математического ожидания и дисперсии смещенного хи-квадрат распределения для матриц параметров NU, DELTA.
>> NU=[10 20; 30 40]
NU =
10 20
30 40
>> DELTA=[1 2; 3 4]
DELTA =
3 5
7 9
>>[M,V] = ncx2stat (NU,DELTA)
M =
11 22
33 44
V =
24 48
72 96
Расположение математического ожидания M и значений (M-3![]() ); (M-2
); (M-2![]() ); (M-
); (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() ) на графике функции
) на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> DELTA=5;
>> NU=10;
>> X=1:0.01:15;
>> Y= ncx2pdf(X,NU,DELTA);
>> plot(X,Y)
>> grid on
>>[M,V] = ncx2stat(NU,DELTA)
M =
15
V =
40
>> sigma=sqrt(V)
sigma =
6.3246
>> H1=line ([M-3*sigma M-3*sigma], [0 ncx2pdf((M-3*sigma),NU,DELTA)+0.02]);
>> set(H1,'Color','m')
>> H2=line ([M-2*sigma M-2*sigma], [0 ncx2pdf((M-2*sigma),NU,DELTA)+ 0.02]);
>> set(H2,'Color','g')
>> H3=line ([M-sigma M-sigma], [0 ncx2pdf((M-sigma),NU,DELTA)+0.02]);
>> set(H3,'Color','c')
>> H4=line ([M M], [0 ncx2pdf((M),NU,DELTA)+0.02]);
>> set(H4,'LineWidth',3, 'Color','k')
>> H5=line ([M+sigma M+sigma], [0 ncx2pdf((M+sigma),NU,DELTA)+0.02]);
>> set(H5,'Color','c')
>> H6=line ([M+2*sigma M+2*sigma], [0 ncx2pdf((M+2*sigma),NU,DELTA)+0.02]);
>> set(H6,'Color','g')
>> H7=line ([M+3*sigma M+3*sigma], [0 ncx2pdf((M+3*sigma),NU,DELTA)+0.02]);
>> set(H7,'Color','m')
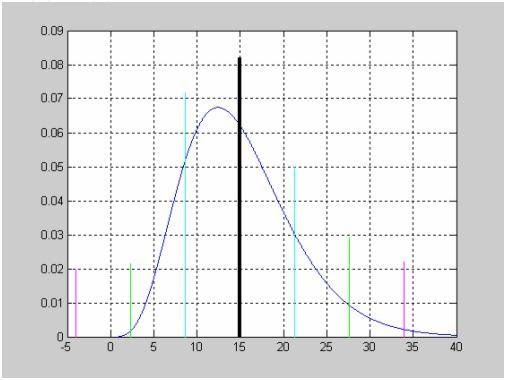
normstat - Нормальное распределение
Синтаксис
[M,V] = normstat(MU,SIGMA)
Описание
[M,V] = normstat(MU,SIGMA) функция служит для расчета математического ожидания и дисперсии нормального закона с заданными параметрами математическим ожиданием MU и средним квадратическим отклонением SIGMA. Размерность векторов и матриц MU, SIGMA должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание нормального закона равно M=MU, дисперсия определяется как
V=SIGMA2.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии нормального закона для пары параметров MU и SIGMA.
>> MU=0
MU =
0
>> SIGMA =1
SIGMA =
1
>> [M,V] = normstat(MU,SIGMA)
M =
0
V =
1
Расчет математического ожидания и дисперсии нормального закона для матриц параметров MU и SIGMA.
>> MU =[0 1 2; 3 4 5]
MU =
0 1 2
3 4 5
>> SIGMA=[1 2 3; 4 5 6]
SIGMA =
1 2 3
4 5 6
>> [M,V] = normstat(MU,SIGMA)
M =
0 1 2
3 4 5
V =
1 4 9
16 25 36
Расположение математического ожидания M и значений (M-3![]() ); (M-2
); (M-2![]() ); (M-
); (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() ) на графике функции
) на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> MU=0;
>> SIGMA =1;
>> X= -4:0.01:4;
>> Y= normpdf(X, MU, SIGMA);
>> plot(X,Y)
>> grid on
>> [M,V] = normstat(MU,SIGMA)
M =
0
V =
1
>> s=sqrt(V)
s =
1
>> H1= line ([M-3*s M-3*s], [0 normpdf(M-3*s,MU,SIGMA)+0.01]);
>> set(H1,'Color','g')
>> H2= line ([M-2*s M-2*s], [0 normpdf(M-2*s,MU,SIGMA)+0.01]);
>> set(H2,'Color','m')
>> H3=line ([M-s M-s], [0 normpdf(M-s,MU,SIGMA)+0.01]);
>> set(H3,'Color','c')
>> H4=line([M M], [0 normpdf(M,MU,SIGMA)+0.01]);
>> set(H4,'LineWidth',3, 'Color','k')
>> H5=line ([M+s M+s], [0 normpdf(M+s,MU,SIGMA)+0.01]);
>> set(H5,'Color','c')
>> H6= line ([M+2*s M+2*s], [0 normpdf(M+2*s,MU,SIGMA)+0.01]);
>> set(H6,'Color','m')
>> H7= line ([M+3*s M+3*s], [0 normpdf(M+3*s,MU,SIGMA)+0.01]);
>> set(H7,'Color','g')
poisstat - Распределение Пуассона
Синтаксис
[M,V] = poisstat(LAMBDA)
Описание
[M,V] = poisstat(LAMBDA) функция служит для расчета математического ожидания и дисперсии распределения Пуассона с заданным параметром LAMBDA. Размерность векторов или матриц M и V совпадает с размерностью входного параметра.
Для распределения Пуассона математическое ожидание и дисперсия равны M=V=LAMBDA .
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии распределения Пуассона для параметра LAMBDA.
>> LAMBDA =1
LAMBDA =
1
>> [M,V] = poisstat(LAMBDA)
M =
1
V =
1
Расчет математического ожидания и дисперсии распределения Пуассона для матрицы параметра LAMBDA.
>> LAMBDA=[1 2 3; 4 5 6]
LAMBDA =
1 2 3
4 5 6
>> [M,V] = poisstat(LAMBDA)
M =
1 2 3
4 5 6
V =
1 2 3
4 5 6
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ], [M-3
], [M-3![]() ; M+3
; M+3![]() ] на графике функции
] на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> LAMBDA=10;
>> X= 0:1:25;
>> Y= poisspdf(X,LAMBDA);
>> plot(X,Y)
>> grid on
>> [M,V] = poisstat(LAMBDA)
M =
10
V =
10
>> sigma=sqrt(V)
sigma =
3.1623
>> H=line ([M M], [0 poisspdf(M,LAMBDA)+0.1]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 poisspdf(floor(M-sigma),LAMBDA)+0.05]);
>> set(H1,'Color','g')
>> H2=line ([M+sigma M+sigma], [0 poisspdf(floor(M+sigma),LAMBDA)+0.05]);
>> set(H2,'Color','g')
>> H3=line ([M-2*sigma M-2*sigma], [0 poisspdf(M-2*sigma, LAMBDA)+0.05]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 poisspdf(M+2*sigma,LAMBDA)+0.05]);
>> set(H4,'Color','m')
>> H5=line ([M-3*sigma M-3*sigma], [0 poisspdf(M-3*sigma,LAMBDA)+0.01]);
>> set(H5,'Color','c')
>> H6=line ([M+3*sigma M+3*sigma], [0 poisspdf(M+3*sigma, LAMBDA)+0.01]);
>> set(H6,'Color','c')
raylstat - Распределение Релея
Синтаксис
[M,V] = raylstat(B)
Описание
[M,V] = raylstat(B) функция служит для расчета математического ожидания и дисперсии распределения Релея с заданным параметром B. Размерность векторов или матриц M и V совпадает с размерностью входного параметра.
Математическое ожидание распределения Релея с заданным параметром B определяется по формуле
![]()
Дисперсия распределения Релея с заданным параметром B определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии распределения Релея для параметра B.
>> B =1
B =
1
>> [M,V] = raylstat(B)
M =
1.2533
V =
0.4292
Расчет математического ожидания и дисперсии распределения Релея для матрицы параметра B.
>> B=[1 2 3; 4 5 6]
B =
1 2 3
4 5 6
>> [M,V] = raylstat(B)
M =
1.2533 2.5066 3.7599
5.0133 6.2666 7.5199
V =
0.4292 1.7168 3.8628
6.8673 10.7301 15.4513
Расположение математического ожидания M и значений (M-2![]() ); (M-
); (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() ) на графике функции
) на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> B=1;
>> X=0:0.01:4;
>> Y= raylpdf(X,B);
>> plot(X,Y)
>> grid on
>> [M,V] = raylstat(B)
M =
1.2533
V =
0.4292
>> sigma=sqrt(V)
sigma =
0.6551
>> H=line ([M M], [0 raylpdf(M,B)+0.05]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 raylpdf((M-sigma,B)+0.05]);
>> set(H1,'Color','g')
>> H2=line ([M+sigma M+sigma], [0 raylpdf(M+sigma,B)+0.05]);
>> set(H2,'Color','g')
>> H3=line ([M-2*sigma M-2*sigma], [0 raylpdf(M-2*sigma, B)+0.05]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 raylpdf(M+2*sigma,B)+0.05]);
>> set(H4,'Color','m')
>> H5=line ([M+3*sigma M+3*sigma], [0 raylpdf(M+3*sigma, B)+0.05]);
>> set(H5,'Color','c')
tstat - Распределение Стьюдента
Синтаксис
[M,V] = tstat(NU)
Описание
[M,V] = tstat(NU функция служит для расчета математического ожидания и дисперсии t распределения с заданным параметром NU. Размерность векторов или матриц M и V совпадает с размерностью входного параметра.
Математическое ожидание t распределения с заданным параметром NU равна M=NU при условии, что NU>1. Для NU![]() 1 математическое ожидание не определено. Дисперсия t распределения с заданным параметром NU определяется по формуле
1 математическое ожидание не определено. Дисперсия t распределения с заданным параметром NU определяется по формуле
![]()
при условии, что NU>2. Для NU![]() 2 дисперсия t распределения не определена.
2 дисперсия t распределения не определена.
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии распределения Стьюдента для параметра NU.
>> NU =10
NU =
10
>> [M,V] = tstat(NU)
M =
0
V =
1.2500
Расчет математического ожидания и дисперсии распределения Стьюдента для матрицы параметра NU.
>> NU=[10 20 30; 40 50 60]
NU =
10 20 30
40 50 60
>> [M,V] = tstat(NU)
M =
0 0 0
0 0 0
V =
1.2500 1.1111 1.0714
1.0526 1.0417 1.0345
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ], [M-3
], [M-3![]() ; M+3
; M+3![]() ] на графике функции
] на графике функции
плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> NU=10;
>> X=-5:0.01:5;
>> Y= tpdf(X,NU);
>> plot(X,Y)
>> grid on
>> [M,V] = tstat(NU)
M =
0
V =
1.2500
>> sigma=sqrt(V)
sigma =
1.1180
>> H=line ([M M], [0 tpdf(M,NU)+0.05]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 tpdf((M-sigma,NU)+0.05]);
>> set(H1,'Color','g')
>> H2=line ([M+sigma M+sigma], [0 tpdf(M+sigma,NU)+0.05]);
>> set(H2,'Color','g')
>> H3=line ([M-2*sigma M-2*sigma], [0 tpdf(M-2*sigma, NU)+0.05]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 tpdf(M+2*sigma,NU)+0.05]);
>> set(H4,'Color','m')
>> H5=line ([M-3*sigma M-3*sigma], [0 tpdf(M-3*sigma, NU)+0.05]);
>> set(H5,'Color','c')
>> H6=line ([M+3*sigma M+3*sigma], [0 tpdf(M+3*sigma, NU)+0.05]);
>> set(H6,'Color','c')
unidstat - Дискретное равномерное распределение
Синтаксис
[M,V] = unidstat(N)
Описание
[M,V] = unidstat(N) ) функция служит для расчета математического ожидания и дисперсии дискретного равномерного распределения с заданным параметром N. Размерность векторов или матриц M и V совпадает размерностью входного параметра.
Математическое ожидание дискретного равномерного распределения с заданным параметром N определяется по формуле
![]()
Дисперсия дискретного равномерного распределения с заданным параметром N определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии дискретного равномерного распределения для параметра N.
>> N =10
N =
10
>> [M,V] = unidstat(N)
M =
5.5000
V =
8.2500
Расчет математического ожидания и дисперсии дискретного равномерного распределения для матрицы параметра N.
>> N=[10 20 30; 40 50 60]
N =
10 20 30
40 50 60
>> [M,V] = unidstat(N)
M =
5.5000 10.5000 15.5000
20.5000 25.5000 30.5000
V =
8.2500 33.2500 74.9167
133.2500 208.2500 299.9167
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ] на графике
] на графике
функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> N=20;
>> X= -2:1:22;
>> Y= unidpdf(X,N);
>> plot(X,Y,'-*')
>> grid on
>> [M,V] = unidstat(N)
M =
10.5000
V =
33.2500
>> sigma=sqrt(V)
sigma =
5.7663
>> H=line ([M M], [0 unidpdf(floor(M),N)+0.005]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 unidpdf(floor(M-sigma),N)+0.005]);
>> set(H1,'Color','g')
>> H2=line ([M+sigma M+sigma], [0 unidpdf(floor(M+sigma),N)+0.005]);
>> set(H2,'Color','g')
>> H3=line ([M-2*sigma M-2*sigma], [0 unidpdf(floor(M-2*sigma), N)+0.005]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 unidpdf(floor(M+2*sigma),N)+0.005]);
>> set(H4,'Color','m')
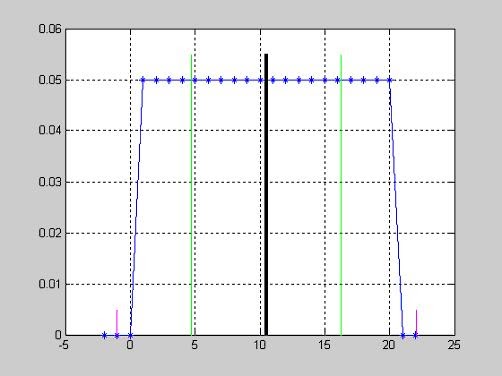
unifstat - Непрерывное равномерное распределение
Синтаксис
[M,V] = unifstat(A,B)
Описание
[M,V] = unifstat(A,B) функция служит для расчета математического ожидания и дисперсии непрерывного равномерного распределения с заданными параметрами А и В. Размерность векторов и матриц А, В должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M непрерывного равномерного распределения с заданными параметрами А и В определяется по формуле
![]()
Дисперсия V непрерывного равномерного распределения с заданными параметрами А и В определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии непрерывного равномерного распределения для пары параметров А и В.
>> A=1
A =
1
>> B=2
B =
2
>> [M,V] = unifstat(A,B)
M =
1.5000
V =
0.0833
Расчет математического ожидания и дисперсии непрерывного равномерного распределения для матриц параметров А и В.
>> A=[1 2 3; 4 5 6]
A =
1 2 3
4 5 6
>> B=[2 3 4; 5 6 7]
B =
2 3 4
5 6 7
>> [M,V] = unifstat(A,B)
M =
1.5000 2.5000 3.5000
4.5000 5.5000 6.5000
V =
0.0833 0.0833 0.0833
0.0833 0.0833 0.0833
Расположение математического ожидания M и интервалов [M-![]() ; M+
; M+![]() ], [M-2
], [M-2![]() ; M+2
; M+2![]() ] на графике
] на графике
функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> A=0;
>> B=20;
>> X= -2:0.1:22;
>> Y= unifpdf(X,A,B);
>> plot(X,Y)
>> grid on
>> [M,V] = unifstat(A,B)
M =
10
V =
33.3333
>> sigma=sqrt(V)
sigma =
5.7735
>> H=line ([M M], [0 unifpdf(M,A,B)+0.005]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 unifpdf(M-sigma,A,B)+0.005]);
>> set(H1,'Color','g')
>> H2=line ([M+sigma M+sigma], [0 unifpdf(M+sigma,A,B)+0.005]);
>> set(H2,'Color','g')
>> H3=line ([M-2*sigma M-2*sigma], [0 unifpdf(M-2*sigma,A,B)+0.005]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 unifpdf(M+2*sigma,A,B)+0.005]);
>> set(H4,'Color','m')
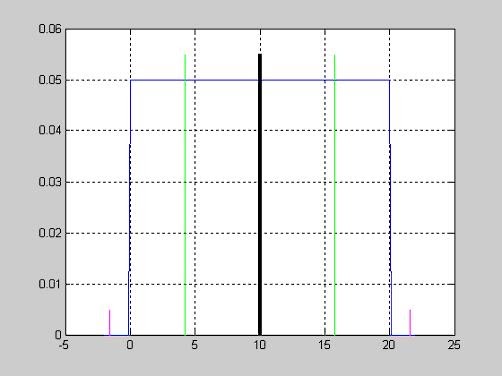
weibstat - Распределение Вейбулла
Синтаксис
[M,V] = weibstat(A,B)
Описание
[M,V] = weibstat(A,B) функция служит для расчета математического ожидания и дисперсии распределения Вейбулла с заданными параметрами А и В. Размерность векторов и матриц А и В должна быть одинаковой. Скалярный входной параметр увеличивается до матрицы постоянных значений с размерностью второго параметра. Размерность матриц математического ожидания M и дисперсии V равна размерности входных параметров.
Математическое ожидание M распределения Вейбулла с заданными параметрами А и В определяется по формуле
![]()
Дисперсия V распределения Вейбулла с заданными параметрами А и В определяется по формуле
![]()
Примеры использования функции оценки математического ожидания и дисперсии
Расчет математического ожидания и дисперсии распределения Вейбулла для пары параметров А и В.
>> A=1
A =
1
>> B=2
B =
2
>> [M,V] = weibstat(A,B)
M =
0.8862
V =
0.2146
Расчет математического ожидания и дисперсии распределения Вейбулла для матриц параметров А и В.
>> A=[1 2 3; 4 5 6]
A =
1 2 3
4 5 6
>> B=[2 3 4; 5 6 7]
B =
2 3 4
5 6 7
>> [M,V] = weibstat(A,B)
M =
0.8862 0.7088 0.6887
0.6958 0.7094 0.7242
V =
0.2146 0.0664 0.0373
0.0254 0.0189 0.0148
Расположение математического ожидания M и значений (M-2![]() ); (M-
); (M-![]() ); (M+
); (M+![]() ); (M+2
); (M+2![]() ); (M+3
); (M+3![]() ) на графике
) на графике
функции плотности вероятности, ![]() - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
>> A=1;
>> B=2;
>> X=0:0.01:3;
>> Y= weibpdf(X,A,B);
>> plot(X,Y)
>> grid on
>> [M,V] = weibstat(A,B)
M =
0.8862
V =
0.2146
>> sigma=sqrt(V)
sigma =
0.4633
>> H=line ([M M], [0 weibpdf(M,A,B)+0.05]);
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line ([M-sigma M-sigma], [0 weibpdf(M-sigma,A,B)+0.05]);
>> set(H1,'Color','g')
>> H2=line ([M+sigma M+sigma], [0 weibpdf(M+sigma,A,B)+0.05]);
>> set(H2,'Color','g')
>> H3=line ([M-2*sigma M-2*sigma], [0 weibpdf(M-2*sigma,A,B)+0.05]);
>> set(H3,'Color','m')
>> H4=line ([M+2*sigma M+2*sigma], [0 weibpdf(M+2*sigma,A,B)+0.05]);
>> set(H4,'Color','m')
>> H5=line ([M+3*sigma M+3*sigma], [0 weibpdf(M+3*sigma,A,B)+0.05]);
>> set(H5,'Color','c')
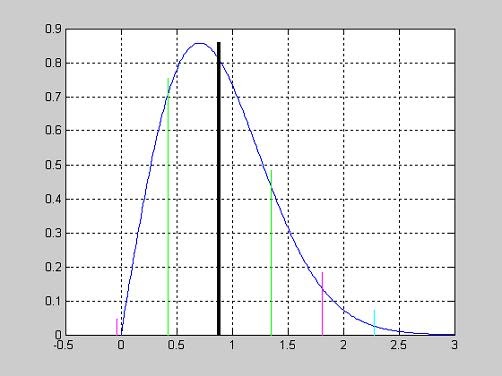
betalike - Расчет логарифма функции максимального правдоподобия бета распределения
Синтаксис
logL = betalike(params,data)
[logL,avar] = betalike(params,data)
Описание
logL = betalike(params,data) функция позволяет рассчитать отрицательный логарифм функции максимального правдоподобия бета распределения с заданными параметрами a, b и исходной выборки. Параметры бета распределения определяются вектором params. Исходная выборка задается вектором data.
[logL,avar] = betalike(params,data) позволяет рассчитать вектор отрицательного логарифма функции максимального правдоподобия logL бета распределения и обратную информационную матрицу Фишера avar. Если параметры бета распределения в векторе params были рассчитаны согласно методу максимального правдоподобия, то avar представляет собой асимптотическое приближение к дисперсионно-ковариационной матрице. Диагональные элементы avar являются асимптотическим приближением к значениям дисперсий соответствующих параметров бета распределения.
betalike является вспомогательной функцией при расчете параметров бета распределения по методу максимального правдоподобия. Исходным предположением метода максимального правдоподобия является взаимная независимость элементов исходной выборки. Вследствие чего, функция betalike возвращает отрицательный логарифм logL функции максимального правдоподобия бета распределения. Минимизация значения logL, возвращаемого функцией betalike, соответствует поиску максимума функции максимального правдоподобия. Такая процедура позволяет определить оптимальные параметры бета распределения по методу максимального правдоподобия.
Примеры использования функции расчета отрицательного логарифма функции максимального правдоподобия бета распределения
Расчет отрицательного логарифма функции максимального правдоподобия.
>> A=4;
>> B=3;
>> params =[A B];
>> data = betarnd(A,B,100,1);
>> logL = betalike(params,data)
logL =
-36.9898
Расчет отрицательного логарифма функции максимального правдоподобия и обратной
информационной матрицы Фишера.
>> A=4;
>> B=3;
>> params =[A B];
>> data = betarnd(A,B,100,1);
>> [logL,avar] = betalike(params,data)
logL =
-23.0818
avar =
0.2356 0.1191
0.1191 0.0858
Как можно видеть из приведенного ниже примера, увеличение объема выборки data на два порядка
приводит к существенному уменьшению величин дисперсий параметров A, B (элементы главной диагонали
матрица avar) и их ковариации (вторая диагональ матрица avar). При этом увеличивается значение
логарифма функции максимального правдоподобия
>> A=4;
>> B=3;
>> params =[A B];
>> data = betarnd(A,B,10000,1);
>> [logL,avar] = betalike(params,data)
logL =
-3.4099e+003
avar =
0.0030 0.0019
0.0019 0.0017
gamlike - Расчет логарифма функции максимального правдоподобия гамма распределения
Синтаксис
logL = gamlike(params,data)
[logL,avar] = gamlike(params,data)
Описание
logL = gamlike(params,data) функция позволяет рассчитать отрицательный логарифм функции максимального правдоподобия Гамма распределения с заданными параметрами a, b и исходной выборки. Параметры бета распределения определяются вектором params. Исходная выборка задается вектором data.
[logL,avar] = gamlike(params,data) позволяет рассчитать вектор отрицательного логарифма функции максимального правдоподобия logL Гамма распределения и обратную информационную матрицу Фишера avar. Если параметры Гамма распределения в векторе params были рассчитаны по методу максимального правдоподобия, то avar представляет собой асимптотическое приближение к дисперсионно-ковариационной матрице. Диагональные элементы avar являются асимптотическим приближением к значениям дисперсий соответствующих параметров Гамма распределения.
gamlike является вспомогательной функцией при расчете параметров Гамма распределения по методу максимального правдоподобия. функция gamlike возвращает отрицательный логарифм logL функции максимального правдоподобия Гамма распределения. Минимизация значения logL, возвращаемого функцией gamlike, соответствует поиску максимума функции максимального правдоподобия. Такая процедура позволяет определить оптимальные параметры Гамма распределения по методу максимального правдоподобия.
Примеры использования функции расчета отрицательного логарифма функции максимального правдоподобия Гамма распределения
Расчет отрицательного логарифма функции максимального правдоподобия.
>> A=4;
>> B=3;
>> params =[A B];
>> data = gamrnd(A,B,100,1);
>> logL = gamlike(params,data)
logL =
337.3935
Расчет отрицательного логарифма функции максимального правдоподобия и обратной информационной матрицы Фишера.
>> A=4;
>> B=3;
>> params =[A B];
>> data = gamrnd(A,B,100,1);
>> [logL,avar] = gamlike(params,data)
logL =
337.3935
avar =
0.2229 -0.1262
-0.1262 0.0830
Как можно видеть из приведенного ниже примера, увеличение объема выборки data на два порядка приводит к существенному
уменьшению величин дисперсий параметров A, B (элементы главной диагонали матрица avar) и их ковариации (вторая диагональ
матрица avar). При этом увеличивается значение логарифма функции максимального правдоподобия
>> A=4;
>> B=3;
>> params =[A B];
>> data = gamrnd(A,B,10000,1);
>> [logL,avar] = gamlike(params,data)
logL =
3.1361e+004
avar =
0.0030 -0.0022
-0.0022 0.0018
normlike - Расчет логарифма функции максимального правдоподобия нормального распределения
Синтаксис
logL = normlike(params,data)
[logL,avar] = normlike(params,data)
Описание
logL = normlike(params,data) функция позволяет рассчитать отрицательный логарифм функции максимального правдоподобия нормального закона с заданными параметрами ![]() ,
, ![]() и исходной выборки, где
и исходной выборки, где ![]() - точечная оценка математического ожидания,
- точечная оценка математического ожидания, ![]() - точечная оценка среднего квадратического отклонения. Параметры нормального закона определяются вектором params: params(1)=
- точечная оценка среднего квадратического отклонения. Параметры нормального закона определяются вектором params: params(1)=![]() , params(2)=
, params(2)= ![]() . Исходная выборка задается вектором data.
. Исходная выборка задается вектором data.
[logL,avar] = normlike(params,data) позволяет рассчитать вектор отрицательного логарифма функции максимального правдоподобия logL нормального закона и обратную информационную матрицу Фишера avar. Если параметры нормального закона в векторе params были рассчитаны по методу максимального правдоподобия, то avar представляет собой асимптотическое приближение к дисперсионно-ковариационной матрице. Диагональные элементы avar являются асимптотическим приближением к значениям дисперсий соответствующих параметров нормального закона.
normlike является вспомогательной функцией при расчете параметров нормального закона по методу максимального правдоподобия для функции mle. функция normlike возвращает отрицательный логарифм logL функции максимального правдоподобия нормального закона. Минимизация значения logL, возвращаемого функцией normlike, соответствует поиску максимума функции максимального правдоподобия. Такая процедура позволяет определить оптимальные параметры нормального закона по методу максимального правдоподобия.
Примеры использования функции расчета отрицательного логарифма функции максимального правдоподобия нормального закона
Расчет отрицательного логарифма функции максимального правдоподобия.
>> MU=0;
>> SIGMA=1;
>> params =[MU SIGMA];
>> data=normrnd(MU,SIGMA,100,1);
>> logL = normlike(params,data)
logL =
137.5246
Расчет отрицательного логарифма функции максимального правдоподобия и обратной информационной матрицы Фишера.
>> MU=0;
>> SIGMA=1;
>> params =[MU SIGMA];
>> data=normrnd(MU,SIGMA,100,1);
>> [logL,avar] = normlike(params,data)
logL =
137.5246
avar =
0.0111 0.0010
0.0010 0.0063
Как можно видеть из приведенного ниже примера, увеличение объема выборки data на два порядка приводит
к существенному уменьшению величин дисперсий параметров MU, SIGMA (элементы главной диагонали матрица avar)
и их ковариаций (вторая диагональ матрица avar). При этом увеличивается значение логарифма функции максимального
правдоподобия
>> MU=0;
>> SIGMA=1;
>> params =[MU SIGMA];
>> data=normrnd(MU,SIGMA,10000,1);
>> [logL,avar] = normlike(params,data)
logL =
1.4208e+004
avar =
1.0e-004 *
0.9963 -0.0023
-0.0023 0.4798
bootstrp - Бутстреп оценки. Оценка статистик для данных с дополненным объемом выборки посредством математического моделирования
Синтаксис
bootstat = bootstrp(nboot,'bootfun',d1,d2,...)
[bootstat,bootsam] = bootstrp(...)
Описание
bootstat = bootstrp(nboot,'bootfun',d1,d2,...) увеличивает в nboot раз размер выборки из исходного набора данных, d1, d2,…, с последующей передачей выборки для анализа в функцию 'bootfun'. Входной аргумент nboot должен быть положительным целым числом. Входные данные должны иметь одинаковое число строк n. Каждая сформированная бутстреп выборка содержит n строк выбранных случайным образом (с замещением) из переданного множества входных данных d1, d2,…
Каждая строка выходной переменной, bootstat, содержит результаты расчета функцией 'bootfun' статистик бутстреп выборок. Если функция 'bootfun' возвращает несколько выходных переменных, bootstat содержит только первую из них. Если первая возвращаемая функцией 'bootfun' переменная является матрицей, то она преобразуется в вектор-столбец. Полученный вектор присваивается выходной переменной bootstat.
[bootstat,bootsam] = bootstrap(...) функция возвращает значения статистик bootstat и матрицу бутстреп индексов bootsam. Каждый из nboot столбцов в матрице bootsam содержит номера значений, которые были извлечены из входного набора данных для составления соответствующей бутстреп выборки. Например, если d1, d2,… содержат по 16 значений и nboot=4, тогда размерность матрицы bootsam будет равна 16x4. первый столбец содержит номера 16 значений извлеченных из d1, d2,… и т.д. для первой из 4 бутстреп выборок, второй столбец содержит индексы для второй бутстреп выборки и т.д. (Бутстреп индексы являются теми же самыми для всех входных наборов данных)
Примеры использования функции расчета бутстреп-оценок выборки
Расчет среднего арифметического значения элементов вектора на 20 элементов. Генерируется 10 бутстреп выборок.
>> X = normrnd(0,1,20,1);
>> [bootstat,bootsam] = bootstrp(10,'mean', X)
bootstat =
-0.0368
-0.1050
0.0818
-0.1837
0.0828
-0.2198
0.1510
0.1348
-0.0164
0.3476
bootsam =
4 5 3 9 13 7 19 9 19 18
7 10 7 9 17 6 16 8 20 15
14 12 9 12 9 12 18 15 10 7
16 16 11 20 19 4 15 12 17 15
12 8 11 8 19 8 14 6 14 14
18 5 5 8 11 15 14 18 7 15
11 13 9 12 7 20 11 12 13 9
20 1 9 7 11 14 9 1 2 5
3 4 14 7 8 4 4 13 8 1
3 11 13 20 14 16 12 15 7 17
18 16 14 13 14 5 17 2 12 18
5 2 2 8 13 11 3 4 18 1
13 7 16 4 3 14 2 10 18 9
1 14 16 2 17 15 9 12 3 3
19 5 7 16 15 7 2 9 9 5
5 18 9 1 8 20 15 9 14 10
20 5 15 12 17 17 16 18 19 9
18 15 10 15 3 19 15 4 9 1
8 6 7 11 18 17 3 8 10 16
11 10 3 7 9 11 16 20 15 10
Графическое представление полученных результатов
>> X = normrnd(0,1,20,1);
>> [bootstat,bootsam] = bootstrp(100,'mean', X);
>> hist(bootstat)
>> grid on
Сравнение результатов расчета среднего арифметического по исходной выборке и средних арифметических значений полученных методом бутстреп оценок
>> X = normrnd(0,1,20,1);
>> m = mean(X)
m =
-0.0826
>> [bootstat,bootsam] = bootstrp(5,'mean', X)
bootstat =
0.0199
-0.7018
-0.1665
-0.2772
-0.3740
bootsam =
16 15 20 1 2
15 13 18 10 12
20 4 16 11 1
20 18 10 18 1
4 19 3 16 5
12 20 13 9 5
4 19 9 20 4
14 3 6 13 5
9 18 17 3 13
2 2 19 7 15
12 9 1 7 3
9 15 14 3 2
13 1 12 6 12
10 11 1 18 5
5 10 12 11 2
11 4 8 5 17
7 18 2 9 15
16 18 5 6 14
1 11 15 1 4
17 4 9 1 11
Графическое представление результатов расчета среднего арифметического по исходной выборке и средних арифметических значений полученных методом бутстреп оценок
>> X = normrnd(0,1,20,1);
>> m = mean(X)
m =
-0.0110
>> [bootstat,bootsam] = bootstrp(100,'mean', X);
>> hist(bootstat)
>> grid on
>> H=line ([m m], [0 25]);
Расчет бутстреп оценки коэффициента эксцесса выборки для матрицы с размерностью 5x5. Генерируется 10 бутстреп выборок.
>> X = normrnd(0,1,5,5);
X =
-1.0082 0.2710 -0.3135 -0.3609 0.4938
-0.6646 1.5350 -0.6022 0.5536 -0.8709
0.5582 -1.0523 1.2591 -1.5564 0.0798
-1.1885 0.6256 0.8585 -0.2067 -0.5216
-0.7755 -0.7976 -2.1053 -0.4256 -1.4139
>> [bootstat,bootsam] = bootstrp(10,'kurtosis', X)
bootstat =
1.1667 1.1667 1.1667 1.1667 1.1667
2.6310 2.4268 1.2410 2.3911 2.3623
3.1957 3.0127 2.9198 3.1830 1.7715
1.2219 1.4334 2.9249 1.4517 1.4670
2.8096 2.6053 1.3214 2.5753 2.5508
2.7328 1.5063 2.0226 2.5297 2.1854
2.7544 2.2273 1.2500 3.2284 2.8191
1.2057 1.1850 3.1529 1.1873 2.2188
1.1667 1.1667 1.1667 1.1667 1.1667
1.6549 1.9115 2.4535 1.2021 2.4930
bootsam =
5 2 4 4 2 2 5 4 1 2
1 4 4 4 3 5 2 3 1 4
1 2 1 3 2 3 1 5 4 1
5 3 4 3 2 4 5 3 4 5
1 4 3 2 4 4 5 4 1 2
>> k = kurtosis(X)
k =
2.8487 1.6520 1.9318 2.5053 1.6952
Расчет коэффициента корреляции методом бутстреп оценок для двух векторов с размерностью 20x1. Генерируется 10 бутстреп выборок. Полученные выборки передаются функции расчета коэффициента корреляции corrcoef. В результате расчета коэффициента корреляции формируется матрица значений bootstat с размерностью 10x4. Т.е., полученная матрица коэффициентов корреляции с размерностью 2x2 преобразуется в вектор с размерностью 1x4. Расчет повторяется для 10 выборок.
>> X1 = normrnd(0,1,20,1);
>> X2 = normrnd(0,1,20,1);
>> [bootstat,bootsam] = bootstrp(10,'corrcoef', X1, X2)
bootstat =
1.0000 0.4900 0.4900 1.0000
1.0000 0.5219 0.5219 1.0000
1.0000 0.3715 0.3715 1.0000
1.0000 0.6003 0.6003 1.0000
1.0000 0.2251 0.2251 1.0000
1.0000 0.3585 0.3585 1.0000
1.0000 0.5380 0.5380 1.0000
1.0000 0.5195 0.5195 1.0000
1.0000 0.4179 0.4179 1.0000
1.0000 0.6214 0.6214 1.0000
bootsam =
15 1 1 1 8 10 12 4 19 10
10 18 10 11 5 13 10 10 20 10
5 15 10 6 15 14 12 18 5 7
15 15 17 20 18 6 6 6 17 19
4 14 11 7 9 14 13 10 5 3
8 10 17 15 7 12 10 7 8 1
1 14 9 11 13 17 4 9 2 16
3 3 16 3 16 19 4 14 5 12
3 18 14 12 18 19 3 11 18 15
20 17 18 8 9 8 8 17 16 11
16 2 2 2 16 17 2 17 15 15
15 5 15 5 3 10 2 16 14 5
20 14 13 5 14 14 19 18 9 2
19 14 12 16 6 13 17 7 5 5
5 16 4 20 13 15 9 8 8 4
12 15 3 19 11 6 9 10 11 17
4 2 9 14 1 17 4 5 9 8
16 6 11 14 10 3 18 8 20 8
20 18 3 9 11 8 11 4 9 3
8 8 1 6 18 11 7 9 7 6
Графическое представление полученных результатов
>> X1 = normrnd(0,1,20,1);
>> X2 = normrnd(0,1,20,1);
>> [bootstat,bootsam] = bootstrp(100,'corrcoef', X1, X2);
>> hist(bootstat(:,2))
>> grid on
corrcoef - Оценка коэффициента корреляции (функция MATLAB)
Синтаксис
R = corrcoef(X)
R = corrcoef(x,y)
[R,P]=corrcoef(...)
[R,P,RLO,RUP]=corrcoef(...)
[...]=corrcoef(...,'param1',val1,'param2',val2,...)
Описание
R = corrcoef(X) функция предназначена для расчета матрицы парных коэффициентов корреляции R выборок представленных в виде матрицы Х. Наблюдения располагаются построчно в матрице Х, выборки - по столбцам.
Расчет (i,j) элемента матрицы R осуществляется по формуле
![]()
где C = cov(X) - матрица ковариаций.
R = corrcoef(x,y) функция предназначена для расчета матрицы парных коэффициентов корреляции R векторов x и y. Тот же результат можно получить при использовании corrcoef([x y]).
[R,P]=corrcoef(...) функция возвращает матрицы парных коэффициентов корреляции R и уровней значимости P, используемых при проверке гипотезы об отсутствии корреляции. Каждое значение Р является значением вероятности получить величину коэффициента корреляции более, чем рассчитанное выборочное значение под действием случайных факторов когда истинное значение коэффициента корреляции равно нулю. Если P(i,j) менее 0,05, то значение коэффициента корреляции R(i,j) является значимым.
[R,P,RLO,RUP]=corrcoef(...) функция возвращает матрицы парных коэффициентов корреляции R, уровней значимости P, нижних RLO и верхних RUP границ 95% доверительных интервалов коэффициентов корреляции.
[...]=corrcoef(...,'param1',val1,'param2',val2,...) в этом варианте синтаксиса функции дополнительные входные параметры определяют:
|
'alpha' |
Значение уровня значимости. Доверительная вероятность определяется как 100*(1 - alpha)%. По умолчанию уровень значимости равен 0,05, что соответствует 95% доверительному интервалу коэффициента корреляции. |
|
'rows' |
Определяет способ исключения строк матрицы Х со значениями NaN при расчете коэффициента корреляции. Возможные значения параметра: 'all' - используются все строки (значение по умолчанию), 'complete' - исключаются строки со значениями NaN, 'pairwise' - при расчете R(i,j) исключаются строки, содержащие NaN в столбце i или j. |
Значения уровня значимости рассчитываются на основе преобразования коэффициента корреляции в t статистику с n-2 степенями свободы, где n - количество строк матрицы Х. Границы доверительного интервала коэффициента корреляции рассчитываются на основании того, что статистика, рассчитанная как 0.5*log((1+R)/(1-R)) имеет асимптотическое приближение к нормальному закону с дисперсией равной 1/(n-3). Рассчитанные таким образом границы доверительного интервала коэффициента корреляции являются точными при больших выборках, когда Х распределены по многомерному нормальному закону. Параметр 'rows' равный 'pairwise' может привести к получения матрицы R которая не будет положительно определенной.
Функция corrcoef является функцией ядра MATLAB.
Примеры использования функции расчета матрицы парных коэффициентов корреляции
Расчет матрицы парных коэффициентов корреляции для 5 выборок с объемом 20 элементов представленных в виде матрицы
>> X = normrnd(0,1,20,5);
>> R = corrcoef(X)
R =
1.0000 0.4873 0.3854 0.0931 -0.2074
0.4873 1.0000 0.6276 -0.3016 -0.3204
0.3854 0.6276 1.0000 -0.4313 -0.4647
0.0931 -0.3016 -0.4313 1.0000 0.1005
-0.2074 -0.3204 -0.4647 0.1005 1.0000
Расчет матрицы парных коэффициентов корреляции для 2 выборок с объемом 20 элементов представленных в виде 2 векторов
>> X = normrnd(0,1,20,1);
>> Y = normrnd(0,1,20,1);
>> R = corrcoef(X,Y)
R =
1.0000 -0.4462
-0.4462 1.0000
Расчет матриц парных коэффициентов корреляции и уровней значимости для 5 выборок с объемом 20 элементов представленных в виде матрицы
>> X = normrnd(0,1,20,5);
>> [R P] = corrcoef(X)
R =
1.0000 -0.1259 0.1972 -0.1178 -0.0923
-0.1259 1.0000 -0.1805 0.2883 0.0972
0.1972 -0.1805 1.0000 0.0367 -0.0704
-0.1178 0.2883 0.0367 1.0000 0.1538
-0.0923 0.0972 -0.0704 0.1538 1.0000
P =
1.0000 0.5970 0.4046 0.6208 0.6987
0.5970 1.0000 0.4463 0.2177 0.6836
0.4046 0.4463 1.0000 0.8780 0.7680
0.6208 0.2177 0.8780 1.0000 0.5175
0.6987 0.6836 0.7680 0.5175 1.0000
Расчет матриц парных коэффициентов корреляции, уровней значимости и границ 95% доверительного интервала для 5 выборок с объемом 20 элементов представленных в виде матрицы
>> X = normrnd(0,1,20,5);
>> [R P RLO RUP] = corrcoef(X)
R =
1.0000 -0.2635 0.1917 -0.0096 -0.1274
-0.2635 1.0000 -0.4230 0.3252 -0.1207
0.1917 -0.4230 1.0000 0.2903 0.2034
-0.0096 0.3252 0.2903 1.0000 0.1955
-0.1274 -0.1207 0.2034 0.1955 1.0000
P =
1.0000 0.2616 0.4181 0.9678 0.5924
0.2616 1.0000 0.0631 0.1618 0.6124
0.4181 0.0631 1.0000 0.2143 0.3897
0.9678 0.1618 0.2143 1.0000 0.4088
0.5924 0.6124 0.3897 0.4088 1.0000
RLO =
1.0000 -0.6323 -0.2741 -0.4502 -0.5395
-0.6323 1.0000 -0.7290 -0.1370 -0.5346
-0.2741 -0.7290 1.0000 -0.1746 -0.2628
-0.4502 -0.1370 -0.1746 1.0000 -0.2704
-0.5395 -0.5346 -0.2628 -0.2704 1.0000
RUP =
1.0000 0.2026 0.5846 0.4347 0.3339
0.2026 1.0000 0.0240 0.6711 0.3400
0.5846 0.0240 1.0000 0.6494 0.5926
0.4347 0.6711 0.6494 1.0000 0.5872
0.3339 0.3400 0.5926 0.5872 1.0000
Расчет матриц парных коэффициентов корреляции, уровней значимости и границ 99% доверительного интервала для 5 выборок с объемом 20 элементов представленных в виде матрицы
>> X = normrnd(0,1,20,5);
>> [R P RLO RUP] = corrcoef(X,'alpha',0.01)
R =
1.0000 0.4454 0.2195 -0.2765 0.2113
0.4454 1.0000 0.2026 0.1240 -0.0572
0.2195 0.2026 1.0000 -0.3124 -0.1067
-0.2765 0.1240 -0.3124 1.0000 -0.1876
0.2113 -0.0572 -0.1067 -0.1876 1.0000
P =
1.0000 0.0491 0.3526 0.2380 0.3712
0.0491 1.0000 0.3916 0.6026 0.8106
0.3526 0.3916 1.0000 0.1800 0.6545
0.2380 0.6026 0.1800 1.0000 0.4284
0.3712 0.8106 0.6545 0.4284 1.0000
RLO =
1.0000 -0.1448 -0.3814 -0.7204 -0.3887
-0.1448 1.0000 -0.3963 -0.4622 -0.5928
-0.3814 -0.3963 1.0000 -0.7388 -0.6242
-0.7204 -0.4622 -0.7388 1.0000 -0.6721
-0.3887 -0.5928 -0.6242 -0.6721 1.0000
RUP =
1.0000 0.8018 0.6899 0.3283 0.6854
0.8018 1.0000 0.6806 0.6348 0.5135
0.6899 0.6806 1.0000 0.2928 0.4759
0.3283 0.6348 0.2928 1.0000 0.4094
0.6854 0.5135 0.4759 0.4094 1.0000
Расчет матриц парных коэффициентов корреляции, уровней значимости и границ 99% доверительного интервала для 5 выборок с объемом 20 элементов представленных в виде матрицы, содержащую нечисловые элементы NaN. Режим исключения нечисловых элементов парный построчный - 'pairwise'.
>> X = normrnd(0,1,20,5);
>> X([1 20 25 36 45 90 99]) = [NaN NaN NaN NaN NaN];
>> [R P RLO RUP] = corrcoef(X,'alpha',0.01,'rows','pairwise')
R =
1.0000 0.1399 -0.0245 0.1995 -0.2121
0.1399 1.0000 0.2357 -0.0335 0.0030
-0.0245 0.2357 1.0000 -0.1962 0.1095
0.1995 -0.0335 -0.1962 1.0000 0.1604
-0.2121 0.0030 0.1095 0.1604 1.0000
P =
1.0000 0.6053 0.9256 0.4274 0.4304
0.6053 1.0000 0.3465 0.8950 0.9913
0.9256 0.3465 1.0000 0.4209 0.6758
0.4274 0.8950 0.4209 1.0000 0.5249
0.4304 0.9913 0.6758 0.5249 1.0000
RLO =
1.0000 -0.5180 -0.6125 -0.4324 -0.7305
-0.5180 1.0000 -0.4011 -0.6035 -0.6116
-0.6125 -0.4011 1.0000 -0.6872 -0.5216
-0.4324 -0.6035 -0.6872 1.0000 -0.4647
-0.7305 -0.6116 -0.5216 -0.4647 1.0000
RUP =
1.0000 0.6938 0.5809 0.7000 0.4614
0.6938 1.0000 0.7188 0.5591 0.6153
0.5809 0.7188 1.0000 0.4180 0.6631
0.7000 0.5591 0.4180 1.0000 0.6788
0.4614 0.6153 0.6631 0.6788 1.0000
Пример генерации матрицы случайны чисел с размерностью 30x4, у которой 4 столбец коррелирован с остальными столбцами
Генерация некоррелированных выборок
>> x = randn(30,4);
Создание 4 столбца коррелированного с первыми тремя
>> x(:,4) = sum(x,2);
Расчет матриц точечных оценок коэффициента корреляции и значений уровня значимости
>> [r,p] = corrcoef(x)
r =
1.0000 -0.3566 0.1929 0.3457
-0.3566 1.0000 -0.1429 0.4461
0.1929 -0.1429 1.0000 0.5183
0.3457 0.4461 0.5183 1.0000
p =
1.0000 0.0531 0.3072 0.0613
0.0531 1.0000 0.4511 0.0135
0.3072 0.4511 1.0000 0.0033
0.0613 0.0135 0.0033 1.0000
Определение индексов значимых коэффициентов корреляции
>> [i,j] = find(p<0.05)
ans =
4 2
4 3
2 4
3 4
cov - Оценка матрицы ковариаций (функция MATLAB)
Синтаксис
C = cov(X)
C = cov(x,y)
Описание
C = cov(X) функция предназначена для расчета ковариационной матрицы C. Если задана одна выборка, Х - вектор, С является дисперсией выборки. Если Х матрица, где строки являются наблюдениями, а столбцы выборками, С представляет собой ковариационную матрицу. По диагонали матрицы С расположены значения дисперсий выборок Х.
C = cov(x,y) функция предназначена для расчета ковариационной матрицы С для двух выборок x, y заданных как векторы-столбцы. Размерность векторов должна совпадать. Тот же результат можно получить при использовании варианта вызова cov([x y]).
Функция cov является функцией ядра MATLAB.
Алгоритм, используемый при расчете ковариационной матрицы
[n,p] = size(X);
X = X - ones(n,1) * mean(X);
Y = X'*X/(n-1);
Примеры использования функции расчета матрицы ковариаций
Расчет ковариационной матрицы для 5 выборок с объемом 20 элементов представленных в виде матрицы
>> X = normrnd(0,1,20,5);
>> C = cov (X)
C =
1.0823 -0.1735 -0.0628 0.2288 -0.1609
-0.1735 1.0714 0.0230 -0.2807 0.0125
-0.0628 0.0230 0.8124 0.0208 -0.0703
0.2288 -0.2807 0.0208 0.9275 0.0782
-0.1609 0.0125 -0.0703 0.0782 0.3810
Расчет ковариационной матрицы для 2 выборок с объемом 20 элементов представленных в виде 2 векторов
>> X = normrnd(0,1,20,1);
>> Y = normrnd(0,1,20,1);
>> C = cov (X,Y)
C =
0.8092 0.2905
0.2905 0.9515
crosstab - Кросстабуляция для нескольких векторов с положительными целыми элементами
Синтаксис
table = crosstab(col1,col2)
table = crosstab(col1,col2,col3,...)
[table,chi2,p] = crosstab(col1,col2)
[table,chi2,p,label] = crosstab(col1,col2)
Описание
table = crosstab(col1,col2) функция выполняет расчет частот повторяемости table пар целых положительных значений векторов col1, col2. Результат расчета выводится в виде матрицы частот table. Размерность матрицы равна m?n, где m - количество значений элементов в векторе col1, n - количество значений элементов в векторе col2. Если векторы col1, col2 содержат вещественные значения, массивы символов, строковые массивы ячеек, то в соответствие каждому значению col1, col2 ставится целое положительное число и выполняется кросс-табуляция по этим числам.
table = crosstab(col1,col2,col3,...) функция возвращает n-мерный массив частот table сочетаний значений векторов col1, col2, col3,..., где n - количество векторов в списке входных переменных. Значение массива table(i,j,k,...) соответствует частоте повторяемости сочетаний значений col1(i), col2(j), col3(k).
[table,chi2,p] = crosstab(col1,col2) функция выполняет расчет частот повторяемости table пар значений векторов col1, col2, значения статистики ![]() chi2, уровня значимости p. Значение статистики chi2 используется для проверки статистической гипотезы о независимости строк и столбцов матрицы частот table. Значение p является уровнем значимости при проверке указанной статистической гипотезы. Значение уровня значимости p близкое к нулю позволяет принять гипотезу о независимости строк и рядов матрицы частот table.
chi2, уровня значимости p. Значение статистики chi2 используется для проверки статистической гипотезы о независимости строк и столбцов матрицы частот table. Значение p является уровнем значимости при проверке указанной статистической гипотезы. Значение уровня значимости p близкое к нулю позволяет принять гипотезу о независимости строк и рядов матрицы частот table.
[table,chi2,p,label] = crosstab(col1,col2) функция кроме частот повторяемости table, значения статистики ![]() chi2, уровня значимости p, возвращает массив ячеек label, содержащий значения входных аргументов, распределенных последовательно по столбцам матрицы. Значение label(i,j) является элементом вектора colj определяющим i-ю группу в j-м измерении.
chi2, уровня значимости p, возвращает массив ячеек label, содержащий значения входных аргументов, распределенных последовательно по столбцам матрицы. Значение label(i,j) является элементом вектора colj определяющим i-ю группу в j-м измерении.
Примеры использования функции кросс-табуляции значений нескольких векторов
Расчет частот повторяемости пар целых положительных значений двух векторов. Значения вектора r1 изменяются в диапазоне 1…3, вектора r2 - в диапазоне 1…2.
>> r1 = unidrnd(3,50,1);
>> r2 = unidrnd(2,50,1);
>> table = crosstab(r1,r2)
table =
7 5
15 8
9 6
Расчет частот повторяемости сочетаний положительных значений трех векторов. Значения вектора r1 изменяются в диапазоне 1…3, вектора r2 - в диапазоне 1…2, вектора r3 - в диапазоне 1...5.
>> r1 = unidrnd(3,50,1);
>> r2 = unidrnd(2,50,1);
>> r3= unidrnd(5,50,1);
>> table = crosstab(r1,r2,r3)
table(:,:,1) =
1 1
3 2
2 2
table(:,:,2) =
0 0
5 1
1 1
table(:,:,3) =
4 1
3 1
2 1
table(:,:,4) =
0 1
3 1
2 1
table(:,:,5) =
2 2
1 3
2 1
Расчет частот повторяемости пар значений двух векторов, значения статистики ![]() , уровня значимости.
, уровня значимости.
>> r1 = unidrnd(3,50,1);
>> r2 = unidrnd(2,50,1);
>> [table,chi2,p] = crosstab(r1,r2)
table =
2 5
10 14
10 9
chi2 =
1.3038
p =
0.5211
Расчет частот повторяемости пар значений двух векторов, значения статистики ![]() , уровня значимости,
, уровня значимости,
а также вывод значений
элементов группируемых векторов.
>> r1 = unidrnd(3,50,1);
>> r2 = unidrnd(2,50,1);
>> [table,chi2,p,label] = crosstab(r1,r2)
table =
7 6
10 15
8 4
chi2 =
2.4103
p =
0.2997
label =
'1' '1'
'2' '2'
'3' []
Пример использования строковых переменных при кросс-табуляции.
>> r1 = ['a b c a b c a b c b c b c']';
>> r2 = ['a b a b a b a b b b b a a']';
>> [table,chi2,p,label] = crosstab(r1,r2)
table =
2 1
2 3
2 3
chi2 =
0.6603
p =
0.7188
label =
'a' 'a'
'b' 'b'
'c' []
geomean - Среднее геометрическое
Синтаксис
m = geomean(X)
Описание
m = geomean(X) - функция предназначена для расчета значения среднего геометрического m выборки Х. Если Х задана как вектор, то среднее геометрическое значение рассчитывается по всем его элементам. Для выборки определенной в виде матрицы среднее геометрическое значение рассчитывается для каждого столбца Х.
Расчет среднего геометрического выборки выполняется по формуле

где n - объем выборки.
Примеры использования функции расчета среднего геометрического значения
Расчет среднего геометрического значения для выборки Х заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> m = geomean(X)
m =
9.8288
Расчет среднего геометрического значения для выборки Х заданной как матрица
>> X = normrnd(10,1,100,5);
>> m = geomean(X)
m =
9.8756 9.9409 9.8043 9.8842 10.0197
Величина среднего геометрического выборки Х должна быть меньше или равна среднему арифметическому значению
>> X = normrnd(10,1,100,5);
>> m = geomean(X)
m =
9.8945 10.0551 9.8076 9.9412 9.8391
>> xbar = mean(X)
xbar =
9.9457 10.0980 9.8506 10.0064 9.8963
grpstats - Сводные статистики по группам
Синтаксис
means = grpstats(X,group)
[means,sem,counts,name] = grpstats(X,group)
[means,sem,counts,name] = grpstats(x,group,alpha)
Описание
means = grpstats(X,group) функция предназначена для расчета среднего арифметического значения means категоризованной переменной Х. Среднее арифметическое значение рассчитывается для каждой категории. Деление на категории выполняется при помощи входного аргумента group. Выборка негруппированных значений Х может быть задана как вектор или матрица. Значения вектора или матрицы Х принадлежат к одной категории, если равны соответствующие значения переменной group. Входной аргумент group может быть представлен как вектор, массив строк или массив ячеек строковых переменных. Также group может быть массивом ячеек, содержащим несколько сгруппированных переменных, например {G1 G2 G3}. В последнем случае наблюдения принадлежат к одной группе, если равны между собой все сгруппированные переменные. Размерность векторов X и group должна совпадать. Если выборка Х задана как матрица, категоризующая переменная group должна быть представлена как вектор. Количество строк матрицы X и элементов вектора group должно быть одинаковым.
[means,sem,counts,name] = grpstats(x,group) функция позволяет рассчитать точечную means и интервальную sem оценки математического ожидания категоризованной переменной Х, количество элементов в каждой категории counts, и отобразить список названий категорий name.
Переменная name полезна для установления соответствия между полученными результатами расчета means, sem и заданными категориями, если элементы group не являются целыми числами.
[means,sem,counts,name] = grpstats(x,group,alpha) этот вариант синтаксиса функции кроме результатов расчета значений means, sem, counts и вывода названий name строит график средних арифметических значений и их 100*(1-alpha)% доверительных интервалов по категориям в порядке возрастания последних.
Примеры использования функции расчета точечной и интервальной оценок математического ожидания категоризованной переменной
Расчет точечной оценки математического ожидания для категоризованной выборки заданной как вектор. Выборка х из 100 наблюдений делится на 4 категории. Категории кодируются целыми числами в диапазоне от 1 до 4.
>> group = unidrnd(4,100,1);
>> x = normrnd(0,1,100,1);
>> means = grpstats(x,group)
means =
0.0369
0.0317
0.0759
0.0454
Расчет точечной оценки математического ожидания для категоризованной выборки заданной в виде матрицы. Переменная Х задается как матрица с размерностью 100x5 и представляет собой 5 выборок по 100 элементов в каждой. Математическое ожидание при генерации выборок изменяется от 1 до 5. Значения в каждой выборке делятся на 4 группы. Категоризующая переменная group задается как вектор целых чисел с размерностью 100x1.
>> group = unidrnd(4,100,1);
>> true_mean = 1:5;
>> true_mean = true_mean(ones(100,1),:);
>> x = normrnd(true_mean,1);
>> means = grpstats(x,group)
means =
1.0369 1.5801 2.8850 4.3252 5.1890
1.0317 1.9425 3.0184 3.8486 4.9424
1.0759 1.9433 2.8528 4.0344 4.6057
1.0454 1.9528 2.9190 3.8409 4.7507
Расчет точечных means и интервальных sem оценок математического ожидания категоризованной переменной Х, количества элементов в каждой категории counts, и отображения списка названий категорий name. Переменная Х задается как матрица с размерностью 100x5. Категории кодируются вектором целых чисел на 4 группы.
>> group = unidrnd(4,100,1);
>> x = normrnd(0,1,100,5);
>> [means,sem,counts,name] = grpstats(x,group)
means =
-0.2741 0.0263 -0.1199 -0.1949 0.0658
0.0205 0.1609 -0.0889 0.1441 -0.1134
-0.2905 0.0505 -0.0386 0.1086 -0.2904
0.5349 -0.0313 0.0819 0.5119 -0.3288
sem =
0.2056 0.1608 0.1764 0.1989 0.1852
0.1506 0.1960 0.2535 0.2000 0.2050
0.1678 0.1209 0.1544 0.1434 0.1537
0.2332 0.2603 0.2468 0.1457 0.1845
counts =
29 29 29 29 29
25 25 25 25 25
29 29 29 29 29
17 17 17 17 17
name =
'1'
'2'
'3'
'4'
Расчет значений means, sem, counts, вывод name и графика средних арифметических значений с 95% доверительными
интервалами по соответствующим категориям.
>> group = unidrnd(4,100,1);
>> x = normrnd(0,1,100,5);
>> [means,sem,counts,name] = grpstats(x,group,0.05)
means =
0.0135 -0.4496 0.0543 0.2349 -0.1285
0.1529 0.2906 -0.1331 0.2133 0.2041
0.1151 0.0340 0.0273 0.1469 0.2279
-0.3031 -0.4670 -0.2492 0.0589 0.2070
sem =
0.2215 0.2651 0.1741 0.2816 0.1873
0.2205 0.1940 0.1795 0.2196 0.1597
0.2330 0.1574 0.2300 0.2046 0.1756
0.2227 0.2238 0.1720 0.2088 0.2229
counts =
19 19 19 19 19
29 29 29 29 29
28 28 28 28 28
24 24 24 24 24
name =
'1'
'2'
'3'
'4'
Расчет значений means, sem, counts и вывод списка категорий name. Переменная Х задается как матрица с размерностью 20x5. Категории определяются строковым массивом и выборка делится на 4 группы.
>> group ={'A' 'B' 'C' 'D' 'A' 'B' 'A' 'B' 'C' 'D' 'C' 'D' 'A' 'A' 'B' 'C' 'D' 'B' 'C' 'D'}'
group =
'A'
'B'
'C'
'D'
'A'
'B'
'A'
'B'
'C'
'D'
'C'
'D'
'A'
'A'
'B'
'C'
'D'
'B'
'C'
'D'
>> x = normrnd(0,1,20,5)
x =
-0.2463 -0.2979 -0.5299 0.8683 0.7193
-0.1457 1.1543 0.5411 -0.8048 -0.2831
-1.1690 1.0461 0.6817 -0.7527 -1.4250
-0.0220 2.1269 0.5386 -0.7458 0.4615
0.6183 -0.6558 -0.5100 -0.3097 1.0915
1.8659 -1.1424 -1.3221 -1.5219 -1.0443
0.0819 0.9490 -0.6107 0.8265 -2.8428
1.6080 -0.4046 -0.5653 -0.6130 0.9968
-0.3807 -0.3843 0.0862 0.9597 0.0765
-1.2996 0.4820 0.6915 1.9730 -1.8667
-0.7240 0.4438 2.1338 0.2950 -0.6136
-0.5650 0.3811 -0.0029 -0.3927 1.1694
0.6217 1.1023 -0.0895 0.5759 -0.5750
-1.3355 0.8564 -0.2550 -1.1414 -0.2648
-0.1231 -1.1785 -0.8742 0.0611 0.0047
-1.1028 0.4020 0.4229 0.0123 -0.0394
-2.7532 -0.5842 -0.1334 -0.1681 -0.5054
0.2520 -0.9795 0.5396 -0.6873 -1.1578
-0.8581 0.1151 0.8752 -0.9907 0.7104
1.1354 0.0685 -1.2508 -0.0498 0.7282
>> [means,sem,counts,name] = grpstats(x,group)
means =
0.3502 -0.8565 -0.5624 0.2891 -0.0456
0.2269 -0.1071 -0.5212 -0.7214 0.4791
-1.2206 0.6396 0.3454 -0.0956 -0.2041
-0.2389 -0.2455 0.0123 0.4581 0.4169
sem =
0.6679 0.3892 0.6913 0.7837 0.3769
0.2133 0.4039 0.5240 0.3131 0.3355
0.5199 0.3487 0.6232 0.2142 0.2502
0.4466 0.2645 0.4143 0.4821 0.3391
counts =
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
name =
'A'
'B'
'C'
'D'
harmmean - Среднее гармоническое
Синтаксис
m = harmmean(X)
Описание
m = harmmean(X) функция предназначена для расчета значения среднего гармонического m выборки Х. Если Х задан как вектор, то среднее гармоническое значение рассчитывается по всем его элементам. Для выборки определенной в виде матрицы среднее гармоническое значение рассчитывается для каждого столбца Х.
Расчет среднего гармонического выборки выполняется по формуле
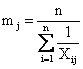
где n - объем выборки.
Примеры использования функции расчета среднего гармонического значения
Расчет среднего гармонического значения выборки Х заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> m = harmmean (X)
m =
9.8263
Расчет среднего гармонического значения выборки Х заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> m = harmmean (X)
m =
10.0391 10.0635 10.0522 10.1031 9.8092
Величина среднего гармонического выборки Х должна быть меньше или равна среднему арифметическому значению
>> X = normrnd(10,1,100,5);
>> m = harmmean (X)
m =
9.8292 10.0088 10.0028 9.9007 9.9302
>> xbar = mean(X)
xbar =
9.9206 10.1203 10.1265 10.0111 10.0221
iqr - Разность между 75% и 25% квантилями или между 3-й и 1-ой квартилями
Синтаксис
y = iqr(X)
Описание
y = iqr(X) функция предназначена для расчета интерквартильного размаха y выборки Х. Интерквартильный размах представляет разницу между 75% и 25% процентилями выборки. Интерквартильный размах является робастной оценкой разброса значений выборки.
Если Х задана как вектор, то интерквартильный размах рассчитывается по всем его элементам. Для выборки определенной в виде матрицы интерквартильный размах рассчитывается для каждого столбца Х.
Интерквартильный размах является более репрезентативной оценкой разброса значений выборки по сравнению с точечной оценкой среднего квадратического отклонения, но менее эффективен при оценке разброса нормально распределенных данных.
Точечная оценка среднего квадратического отклонения для нормально распределенной генеральной совокупности может быть получена как произведение интерквартильного размаха на 0,7413.
Примеры использования функции расчета интерквартильного размаха выборки
Расчет интерквартильного размаха выборки Х, заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> y = iqr(X)
y =
1.3242
Расчет интерквартильного размаха выборки Х, заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> y = iqr(X)
y =
1.4223 1.4877 1.3366 0.9497 1.7574
Определение эффективности точечной оценки среднего квадратического отклонения, рассчитанной как произведение
интерквартильного размаха выборки на 0,7413, для 100 нормально распределенных выборок.
>> X = normrnd(0,1,100,100);
>> s = std(X);
>> s_IQR = 0.7413 * iqr(X);
>> efficiency = (norm(s - 1)./norm(s_IQR - 1)).^2
efficiency =
0.5409
kurtosis - Оценка коэффициента эксцесса (в отечественной литературе коэффициент эксцесса определяется как b2=kurtosis-3)
Синтаксис
k = kurtosis(X)
k = kurtosis(X,flag)
Описание
k = kurtosis(X) функция предназначена для расчета точечной оценки коэффициента эксцесса k выборки Х. Если Х задана как вектор, то точечная оценка коэффициента эксцесса рассчитывается по всем его элементам. Для выборки определенной в виде матрицы точечная оценка коэффициента эксцесса рассчитывается для каждого столбца Х.
Расчет точечной оценки коэффициента эксцесса выборки выполняется по формуле
![]() ,
,
где ![]() - среднее арифметическое значение выборки
- среднее арифметическое значение выборки ![]() ,
, ![]() - точечная оценка среднего квадратического отклонения выборки
- точечная оценка среднего квадратического отклонения выборки ![]() ,
, ![]() - наиболее вероятная оценка параметра t.
- наиболее вероятная оценка параметра t.
Коэффициент эксцесса показывает насколько выборка Х по наклону кривой функции плотности вероятности соответствует нормальному закону. Для нормального закона коэффициент эксцесса равен 3. Законы распределения с более острой вершиной, чем у нормального имеют коэффициент эксцесса более 3 и с менее острой вершиной - менее 3.
Примечание: в отечественной литературе коэффициент эксцесса определяется по формуле ![]() . Таким образом, коэффициент эксцесса нормального закона равен 0.
. Таким образом, коэффициент эксцесса нормального закона равен 0.
k = kurtosis(X,flag) функция позволяет рассчитать несмещенную (flag=0) и смещенную (flag=1, значение по умолчанию) точечную оценку коэффициента эксцесса k выборки Х. Величина смещения выборочного коэффициента эксцесса зависит от объема выборки. Если Х является выборкой из генеральной совокупности, для получения несмещенной точечной оценки коэффициента эксцесса flag должен быть равен 0.
Примеры использования функции расчета точечной оценки коэффициента эксцесса выборки
Расчет точечной оценки коэффициента эксцесса выборки Х, заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> k = kurtosis(X)
k =
2.6987
Расчет точечной оценки коэффициента эксцесса выборки Х заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> k = kurtosis(X)
k =
2.4775 2.9325 2.6933 3.0013 3.0669
Расчет смещенной и несмещенной точечных оценок коэффициента эксцесса выборки Х
>> X = normrnd(10,1,100,1);
>> k = kurtosis(X,1)
k =
2.7772
>> k = kurtosis(X,0)
k =
-0.1718
Сравнение распределения выборок и значений коэффициента эксцесса для нормального закона и закона Вейбулла
>> X1 = normrnd(10,1,100,1);
>> X2 = weibrnd(2,1,100,1);
>> X = [X1 X2];
>> k = kurtosis(X)
k =
3.1280 4.5821
>> histfit(X1)
>> grid on
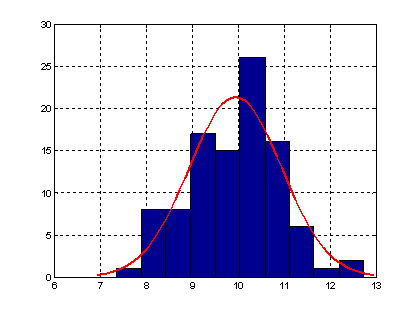
>> histfit(X2)
>> grid on
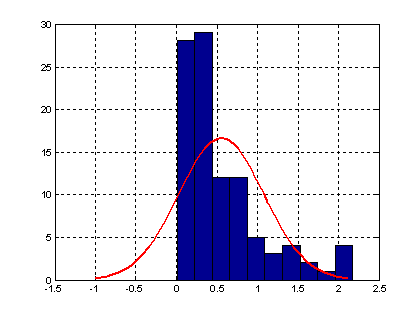
mad - Среднее абсолютное отклонение от среднего значения
Синтаксис
y = mad(X)
Описание
y = mad(X) функция предназначена для расчета среднего абсолютного отклонения y выборки Х от среднего арифметического значения. Выборка Х может быть представлена в виде вектора или матрицы. Если Х задана как вектор, то среднее абсолютное отклонение значений выборки рассчитывается по всем его элементам. Для выборки определенной в виде матрицы среднее абсолютное отклонение рассчитывается для каждого столбца Х.
Среднее абсолютное отклонение является менее эффективной оценкой разброса значений выборки из нормально распределенной генеральной совокупности по сравнению с точечной оценкой среднего квадратического отклонения.
Для нормально распределенной генеральной совокупности точечная оценка среднего квадратического отклонения равна произведению среднего абсолютного отклонения на 1,3.
Примеры использования функции расчета среднего абсолютного отклонения значений выборки
Расчет среднего абсолютного отклонения выборки Х заданной как вектор
>> X = normrnd(10,1,100,1);
>> y = mad(X)
y =
0.7325
Расчет среднего абсолютного отклонения выборки Х, заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> y = mad(X)
y =
0.7628 0.9216 0.8363 0.7577 0.8859
Определение эффективности точечной оценки среднего квадратического отклонения, рассчитанной как произведение
среднего абсолютного отклонения на 1,3, для 100 нормально распределенных выборок.
>> X = normrnd(0,1,100,100);
>> s = std(X);
>> s_MAD = 1.3 * mad(X);
>> efficiency = (norm(s - 1)./norm(s_MAD - 1)).^2
efficiency =
0.6730
moment - Оценка центрального момента. Порядок момента задается как аргумент функции
Синтаксис
m = moment(X,k)
Описание
m = moment(X,k) функция предназначена для расчета центрального момента m порядка k выборки X. Значение порядка момента k должно быть целым положительным числом. Если Х задана как вектор, то центральный момент m рассчитывается по всем его элементам. Для выборки определенной в виде матрицы центральный момент m рассчитывается для каждого столбца Х.
Первый центральный момент равен нулю. Второй центральный момент является точечной оценкой дисперсии и определяется по формуле
![]() ,
,
где M[X]j - математическое ожидание выборки, n - объем выборки (число элементов в векторе, или строк в матрице Х).
Центральный момент k-го порядка рассчитывается по формуле
![]() ,
,
где ![]() - среднее арифметическое значение выборки Xj , E(t) - наиболее вероятная оценка параметра t.
- среднее арифметическое значение выборки Xj , E(t) - наиболее вероятная оценка параметра t.
Примеры использования функции расчета центрального момента произвольного порядка выборки
Расчет второго центрального момента (точечной оценки дисперсии) выборки Х, заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> m = moment(X,2)
m =
0.7940
Расчет второго центрального момента (точечной оценки дисперсии) выборки Х, заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> m = moment(X,2)
m =
0.7615 0.7820 0.9083 0.8813 1.1147
nanmax - Максимальное значение в выборке. Нечисловые значения в выборке игнорируются
Синтаксис
m = nanmax(Х)
[m,ndx] = nanmax(Х)
m = nanmax(Х,Y)
Описание
m = nanmax(Х) функция предназначена для поиска максимального значения m в выборке Х содержащей значения элементов равные NaN. Нечисловые значения элементов матрицы Х NaN рассматриваются как пропущенные. Если Х задана как вектор, то поиск максимального значения производится по всем его элементам. Для выборки определенной в виде матрицы поиск максимального значения выполняется для каждого столбца Х.
[m,ndx] = nanmax(Х) функция поиска максимального значения m и номеров максимальных значений ndx в выборке Х, содержащей значения элементов равные NaN. Номера максимальных значений ndx представляются в виде вектора.
m = nanmax(Х,Y) функция выполняет поиск максимальных элементов m матриц Х и Y с игнорированием элементов со значениями равными NaN. Сравнение соответствующих элементов матриц X, Y выполняется попарно. Размерности Х и Y должны совпадать. Результатом является матрица m с размерностью матриц Х и Y.
Примеры использования функции поиска максимального значения в выборке содержащей нечисловые элементы
Поиск максимального значения выборки Х, заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> X([1 10 50 66 54]) = [NaN NaN NaN NaN NaN];
>> m = nanmax(Х)
m =
12.1832
Поиск максимальных значений выборок в матрице Х
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> m = nanmax(Х)
m =
12.1122 12.3093 12.3726 11.8705 12.6903
Поиск максимальных значений выборок и их индексов в матрице Х
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> [m,ndx] = nanmax(Х)
m =
12.1764 12.7316 12.4953 11.7621 12.9495
ndx =
67 56 36 52 77
Поиск максимальных элементов матриц Х и Y с игнорированием элементов равных NaN
>> X = normrnd(10,1,5,5);
>> Y = normrnd(10,1,5,5);
>> X([1 7 12 15 25]) = [NaN NaN NaN NaN NaN];
>> Y([2 6 11 16 23]) = [NaN NaN NaN NaN NaN];
>> m = nanmax(Х,Y)
m =
7.0228 11.6830 12.2472 11.4445 9.5813
11.6275 10.5553 10.0032 9.9256 11.4149
10.8844 10.7595 11.9916 10.2624 9.1526
9.5941 10.0967 11.6241 10.1192 10.1661
9.8473 11.1580 10.1396 10.3323 10.9260
nanmean - Среднее арифметическое выборки. Нечисловые значения в выборке игнорируются
Синтаксис
y = nanmean(X)
Описание
y = nanmean(X) функция предназначена для расчета среднего арифметического y выборки Х содержащей значения элементов равные NaN. Нечисловые значения элементов матрицы Х NaN рассматриваются как пропущенные. Если Х задана как вектор, то расчет среднего арифметического производится по всем его элементам. Для выборки определенной в виде матрицы расчет среднего арифметического выполняется для каждого столбца Х.
Примеры использования функции расчета среднего арифметического выборки содержащей нечисловые элементы
Расчет среднего арифметического выборки, заданной как вектор
>> X = normrnd(10,1,100,1);
>> X([1 10 50 66 54]) = [NaN NaN NaN NaN NaN];
>> y = nanmean (Х)
y =
10.0669
Расчет средних арифметических значений выборок, заданных в виде матрицы
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> y = nanmean (Х)
y =
9.9490 10.1019 9.8540 9.9973 9.8967
nanmedian - Медиана выборки. Нечисловые значения в выборке игнорируются
Синтаксис
y = nanmedian(X)
Описание
y = nanmedian(X) функция предназначена для расчета медианы y выборки Х, содержащей значения элементов равные NaN. Нечисловые значения элементов матрицы Х NaN рассматриваются как пропущенные. Если Х задана как вектор, то расчет медианы производится по всем его элементам. Для выборки определенной в виде матрицы расчет медианы выполняется для каждого столбца Х.
Примеры использования функции расчета медианы выборки с нечисловыми элементами
Расчет медианы выборки, заданной как вектор
>> X = normrnd(10,1,100,1);
>> X([1 10 50 66 54]) = [NaN NaN NaN NaN NaN];
>> y = nanmedian (Х)
y =
9.8785
Расчет медиан выборок, заданных в виде матрицы
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> y = nanmedian (Х)
y =
10.2096 10.1491 10.2606 10.1257 9.9874
nanmin - Минимальное значение в выборке. Нечисловые значения в выборке игнорируются
Синтаксис
m = nanmin(Х)
[m,ndx] = nanmin(a)
m = nanmin(a,b)
Описание
m = nanmin(Х) функция предназначена для поиска минимального значения m в выборке Х содержащей значения элементов равные NaN. Нечисловые значения элементов матрицы Х NaN рассматриваются как пропущенные. Если Х задана как вектор, то поиск минимального значения производится по всем его элементам. Для выборки определенной в виде матрицы поиск минимального значения выполняется для каждого столбца Х.
[m,ndx] = nanmin(Х) функция поиска минимального значения m и номеров минимальных значений ndx в выборке Х, содержащей значения элементов равные NaN. Номера минимальных значений ndx представляются в виде вектора.
m = nanmin(X,Y) функция выполняет поиск минимальных элементов m матриц Х и Y с игнорированием элементов со значениями равными NaN. Сравнение соответствующих элементов матриц X, Y выполняется попарно. Размерности Х и Y должны совпадать. Результатом является матрица m с размерностью матриц Х и Y.
Примеры использования функции поиска минимального значения в выборке содержащей нечисловые элементы
Поиск минимального значения выборки Х, заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> X([1 10 50 66 54]) = [NaN NaN NaN NaN NaN];
>> m = nanmin(Х)
m =
7.9151
Поиск минимальных значений выборок в матрице Х
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> m = nanmin(Х)
m =
8.3019 7.6298 6.4973 6.7146 7.3728
Поиск минимальных значений выборок и их индексов в матрице Х
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> [m,ndx] = nanmin(Х)
m =
7.6796 7.8707 7.9710 8.0647 7.3797
ndx =
71 75 29 19 37
Поиск минимальных элементов матриц Х и Y с игнорированием нечисловых элементов
>> X = normrnd(10,1,5,5);
>> Y = normrnd(10,1,5,5);
>> X([1 7 12 15 25]) = [NaN NaN NaN NaN NaN];
>> Y([2 6 11 16 23]) = [NaN NaN NaN NaN NaN];
>> m = nanmin(Х,Y)
m =
11.0258 11.2535 10.3844 12.2433 10.3521
8.1952 11.0665 9.3263 9.8507 9.9351
10.5221 6.9539 10.0804 9.1112 9.9209
9.7920 9.7282 11.2769 8.2508 9.8360
9.7798 9.7111 10.5591 7.8597 9.3344
nanstd - Оценка среднего квадратического отклонения выборки. Нечисловые значения в выборке игнорируются
Синтаксис
y = nanstd(X)
Описание
y = nanstd(X) функция предназначена для расчета точечной оценки среднего квадратического отклонения y выборки Х, содержащей значения элементов равные NaN. Нечисловые значения элементов матрицы Х NaN рассматриваются как пропущенные. Если Х задана как вектор, то расчет точечной оценки среднего квадратического отклонения производится по всем его элементам. Для выборки определенной в виде матрицы расчет точечной оценки среднего квадратического отклонения выполняется для каждого столбца Х.
Примеры использования функции расчета точечной оценки среднего квадратического отклонения выборки с нечисловыми элементами
Расчет точечной оценки среднего квадратического отклонения выборки, заданной как вектор
>> X = normrnd(10,1,100,1);
>> X([1 10 50 66 54]) = [NaN NaN NaN NaN NaN];
>> y = nanstd(X)
y =
0.9424
Расчет точечных оценок среднего квадратического отклонения выборок, заданных в виде матрицы
>> X = normrnd(10,1,100,5);
>> X([1 120 250 366 454]) = [NaN NaN NaN NaN NaN];
>> y = nanstd(X)
y =
1.0444 1.0968 1.0272 0.9683 1.1566
prctile - Выборочная процентная точка (процентиль)
Синтаксис
Y = prctile(X,p)
Описание
Y = prctile(X,p) функция предназначена для расчета процентилей Y выборки X, соответствующих вероятности попадания случайной величины в интервал (-![]() ,Y] с вероятностью p. Значение вероятности p должно находиться в интервале от 0 до 100%.
,Y] с вероятностью p. Значение вероятности p должно находиться в интервале от 0 до 100%.
Если Х задана как вектор, то процентиль Y рассчитывается по всем его элементам для вероятности p. Вероятность p может быть задана как скаляр или вектор. Значения процентили рассчитываются для каждого элемента вектора p.
Для выборки определенной в виде матрицы процентиль рассчитывается для каждого столбца Х. Для матрицы Х и вектора р процентиль рассчитывается для всех значений p и для каждого столбца. Размерность матрицы Y равна mxn, где m - число элементов вектора p, n - число столбцов матрицы Х.
Примеры использования функции расчета процентилей выборки
Расчет 10% процентили вектора Х
>> X = normrnd(0,1,100,1);
>> p=10;
>> Y = prctile(X,p)
Y =
-1.1015
Расчет 10%, 20%, 30% процентилей вектора Х
>> X = normrnd(0,1,100,1);
>> p=[10 20 30];
>> Y = prctile(X,p)
Y =
-1.2258 -1.0402 -0.6829
Расчет 10% процентилей для нескольких выборок матрицы Х
>> X = normrnd(0,1,100,5);
>> p=10;
>> Y = prctile(X,p)
Y =
-1.2635 -1.1216 -1.3599 -1.3920 -1.0285
Расчет 10%, 20%, 30% процентилей для нескольких выборок матрицы Х
>> X = normrnd(0,1,100,5);
>> p=[10 20 30];
>> Y = prctile(X,p)
Y =
-1.4662 -1.2327 -1.4568 -1.5269 -1.4533
-0.9595 -0.7126 -1.0071 -0.9093 -0.9905
-0.5902 -0.2939 -0.6884 -0.5700 -0.6566
Графическое представление 10%, 30%, 50%, 70%, 90% процентилей выборки Х
>> X = normrnd(0,1,100,1);
>> p=[10 30 50 70 90];
>> Y = prctile(X,p)
Y =
-1.1015 -0.3344 0.1162 0.5745 1.1421
>> hist(X)
>> grid on
>> H=line ([Y(1) Y(1)], [0 25]);
>> H1=line ([Y(2) Y(2)], [0 25]);
>> H2=line ([Y(3) Y(3)], [0 25]);
>> H3=line ([Y(4) Y(4)], [0 25]);
>> H4=line ([Y(5) Y(5)], [0 25]);
range - Размах выборки
Синтаксис
R = range(X)
Описание
R = range(X) функция предназначена для расчета размаха R выборки Х. Если Х задана как вектор, то размах рассчитывается по всем его элементам. Для выборки определенной в виде матрицы размах рассчитывается для каждого столбца Х.
Расчет размаха выполняется по формуле
![]()
Размах является точечной оценкой разброса значений выборки. Размах чувствителен к грубым промахам, что делает его ненадежной оценкой разброса.
Примеры использования функции расчета размаха выборки
Расчет размаха выборки Х заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> R = range(X)
R =
5.7830
Расчет размаха выборки Х заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> R = range(X)
R =
4.4707 6.2069 5.4199 4.2831 4.5227
Оценка влияния грубых промахов на величину размаха
>> X = normrnd(10,1,100,1);
>> R = range(X)
R =
4.9442
>> X(100,1) =-8;
>> R = range(X)
R =
20.8149
skewness - Оценка коэффициента асимметрии
Синтаксис
y = skewness(X)
y = skewness(X,flag)
Описание
y = skewness(X) функция предназначена для расчета точечной оценки коэффициента асимметрии y выборки Х. Если Х задана как вектор, то точечная оценка коэффициента асимметрии рассчитывается по всем его элементам. Для выборки определенной в виде матрицы точечная оценка коэффициента асимметрии рассчитывается для каждого столбца Х.
Расчет проводится по формуле
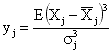 ,
,
где ![]() - среднее арифметическое значение выборки Х,
- среднее арифметическое значение выборки Х, ![]() - точечная оценка среднего квадратического отклонения выборки Х, E(t) - наиболее вероятная оценка параметра t.
- точечная оценка среднего квадратического отклонения выборки Х, E(t) - наиболее вероятная оценка параметра t.
Коэффициент асимметрии выборки является мерой смещенности распределения относительно среднего арифметического значения.
Отрицательный коэффициент асимметрии соответствует распределению смещенному влево относительно среднего значения. Положительный коэффициент асимметрии соответствует распределению смещенному вправо относительно среднего значения. Для нормального закона, или любого другого симметричного распределения, коэффициент асимметрии равен нулю.
y = skewness(X,flag) функция позволяет рассчитать несмещенную (flag=0) и смещенную (flag=1, значение по умолчанию) точечную оценку коэффициента асимметрии y выборки Х. Величина смещения выборочного коэффициента асимметрии зависит от объема выборки. Если Х является выборкой из генеральной совокупности, для получения несмещенной точечной оценки коэффициента асимметрии flag должен быть равен 0.
Примеры использования функции расчета точечной оценки коэффициента асимметрии выборки
Расчет точечной оценки коэффициента асимметрии выборки Х, заданной в виде вектора
>> X = normrnd(10,1,100,1);
>> y = skewness (X)
y =
0.1302
Расчет точечной оценки коэффициента асимметрии выборки Х заданной в виде матрицы
>> X = normrnd(10,1,100,5);
>> y = skewness (X)
y =
0.2924 -0.3086 0.0883 0.0849 0.2744
Расчет смещенной и несмещенной точечных оценок коэффициента асимметрии выборки Х
>> X = normrnd(10,1,100,1);
>> y = skewness (X,1)
y =
0.6063
>> y = skewness (X,0)
y =
0.6156
Сравнение распределения выборок и значений коэффициента асимметрии для нормального закона и закона Вейбулла
>> X1 = normrnd(10,1,100,1);
>> X2 = weibrnd(2,1,100,1);
>> X = [X1 X2];
>> y = skewness (X)
y =
-0.3116 2.5254
>> histfit(X1)
>> grid on
>> histfit(X2)
>> grid on
tabulate - Определение частот целых положительных элементов вектора случайных значений
Синтаксис
table = tabulate(x)
tabulate(x)
Описание
table = tabulate(x) функция позволяет получить матрицу table частот элементов вектора х. Элементы вектора х должны быть целыми положительными числами. Матрица table содержит три столбца. В первом столбце содержатся значения элементов вектора х, во втором - частота значений, в третьем - относительная частота значений, выраженная в процентах от объема выборки.
tabulate(x) вариант синтаксиса функции без выходных аргументов выводит матрицу частот в виде отформатированной таблицы.
Примеры использования функции расчета частот элементов вектора
Расчет матрицы частот элементов вектора
>> x = unidrnd(5,50,1);
>> table = tabulate(x)
table =
1 14 28
2 12 24
3 6 12
4 6 12
5 12 24
Расчет матрицы частот элементов вектора и вывод форматированной таблицы
>> x = unidrnd(5,50,1);
>> tabulate(x)
Value Count Percent
1 14 28.00%
2 12 24.00%
3 6 12.00%
4 6 12.00%
5 12 24.00%
trimmean - Оценка среднего арифметического значения, находимая с игнорированием заданного процента минимальных и максимальных элементов в выборки
Синтаксис
m = trimmean(X,percent)
Описание
m = trimmean(X,percent) функция предназначена для расчета среднего арифметического m выборки X с исключением заданного процента наблюдений percent в выборке. Исключение выполняется для минимальных и максимальных значений с долей наблюдений равной percent/2. Полученная оценка математического ожидания является робастной. Если данные принадлежат к одному распределению, то среднее арифметическое полученное с игнорированием заданного процента наблюдений мене эффективно по сравнению со средним арифметическим.
Если Х задана как вектор, то среднее арифметическое значение рассчитывается по всем его элементам. Для выборки определенной в виде матрицы среднее арифметическое значение рассчитывается для каждого столбца Х.
Для Х заданной как матрица (набор выборок) можно определить вектор percent для каждой выборки отдельно. В этом случае число элементов в векторе percent должно быть равно числу столбцов Х.
Примеры использования функции расчета среднего арифметического значения выборки с исключением заданного процента минимальных и максимальных элементов в выборке
Расчет среднего арифметического значения выборки с игнорированием 5% минимальных и 5% максимальных значений выборки заданной как вектор
>> X=normrnd(0,1,100,1);
>> percent = 10
percent =
10
>> m = trimmean(X,percent)
m =
0.0594
Расчет среднего арифметического значения выборки с игнорированием 5% минимальных и 5% максимальных значений выборки заданной как матрица
>> X=normrnd(0,1,100,5);
>> percent = 10
percent =
10
>> m = trimmean(X,percent)
m =
0.0582 -0.0580 0.1150 -0.1523 0.0109
Расчет средних арифметических значений 5 выборок с игнорированием 5%, 10%, 7%, 12%, 20% минимальных и максимальных значений для каждой выборки
>> X=normrnd(0,1,100,5);
>> percent = [5 10 7 12 20]
percent =
5 10 7 12 20
>> m = trimmean(X,percent)
m =
-0.1101 -0.0970 0.1581 0.1432 0.1737
Оценка эффективности среднего арифметического с 10% исключением максимальных и минимальных значений по сравнению со средним арифметическим, рассчитанных без исключения элементов выборки.
>> x = normrnd(0,1,100,100);
>> m = mean(x);
>> trim = trimmean(x,10);
>> sm = std(m);
>> strim = std(trim);
>> efficiency = (sm/strim).^2
efficiency =
0.9684
Оценка эффективности среднего арифметического с 10% исключением максимальных и минимальных значений по сравнению со средним арифметическим, рассчитанных без исключения элементов выборки.
>> x = normrnd(0,1,100,100);
>> m = mean(x);
>> trim = trimmean(x,10);
>> sm = std(m);
>> strim = std(trim);
>> efficiency = (sm/strim).^2
efficiency =
0.9684
capable - Расчет индексов воспроизводимости процесса Cp, Сpk
Синтаксис
p = capable(data,specs)
[p,Cp,Cpk] = capable(data,specs)
Описание
p = capable(data,specs) функция позволяет рассчитать вероятность р выхода значений выборки data за границы допусков specs. Выборка data задается как вектор. Границы допусков представляются в виде двухэлементного вектора: specs(1) - нижняя граница допуска, specs(2) - верхняя граница допуска.
Исходными предположениями при расчете p являются:
-
не противоречие выборки data нормальному закону с постоянными математическим ожиданием и дисперсией,
-
статистической независимостью результатов измерений в выборке.
[p,Cp,Cpk] = capable(data,specs) позволяет рассчитать вероятность р выхода значений выборки data за границы допусков specs, индексы воспроизводимости процесса Cp, Cpk
Расчет среднего арифметического значения элементов вектора на 20 элементов. Генерируется 10 бутстреп выборок.
Индекс Cp (индекс потенциальной пригодности) представляет собой отношение разности верхней USL и нижней LSL границ поля допуска к произведению ![]() , где
, где ![]() - точечная оценка среднего квадратического отклонения выборки:
- точечная оценка среднего квадратического отклонения выборки:
![]()
Для центрированного технологического процесса (выборочное среднее совпадает с номинальным значением параметра технологического процесса) значение Cp=1 соответствует отношению числа дефектов к числу изделий равному 1/1000. Согласно положениям метода "шесть сигма" долю дефектов необходимо снижать до величин 10/1000000 и менее. Величина доли дефектов 1/1000000 соответствует значению Cp=1.6. Таким образом, уменьшение величины коэффициента Cp соответствует улучшению качества технологического процесса по уровню дефектности при центрированном технологическом процессе.
Индекс Cpk (индекс смещенности технологического процесса) рассчитывается по формуле
![]()
где ![]() - среднее арифметическое выборки data.
- среднее арифметическое выборки data.
Из приведенной выше формулы следует, что индекс воспроизводимости Cpk является отношением минимальной разности среднего арифметического выборки data и верхней или нижней границы поля допуска параметра к трем точечным оценкам среднего квадратического отклонения. Индекс Cpk=1 для центрированного технологического процесса при Cp=1
Примеры использования функции расчета индексов воспроизводимости
Расчет вероятности брака.
>> data=normrnd(0,1,100,1);
>> specs=[-2 2];
>> p = capable(data,specs)
p =
0.0413
Расчет вероятности брака и индексов воспроизводимости процесса Cp , Cpk .
>> data=normrnd(0,1,100,1);
>> specs=[-2 2];
>> [p,Cp,Cpk] = capable(data,specs)
p =
0.0216
Cp =
0.7672
Cpk =
0.7452
Пример центрированного процесса с границами рассеяния параметра (![]() ±3
±3![]() ) совпадающими с границами допусков.
) совпадающими с границами допусков.
>> data=normrnd(0,1,100,1);
>> specs=[-3 3];
>> [p,Cp,Cpk] = capable(data,specs)
p =
0.0013
Cp =
1.0856
Cpk =
1.0316
Графическое представление центрированного технологического процесса
с границами рассеяния параметра совпадающими с границами допусков.
>> data=normrnd(0,1,100,1);
>> specs=[-3 3];
>> [p,Cp,Cpk] = capable(data,specs)
p =
0.0013
Cp =
1.0856
Cpk =
1.0316
>> capaplot(data,specs)
>> H = line([0 0],[0 0.5])
>> set(H,'LineWidth',3, 'Color','k')
>> H1=line([specs(1) specs(1)],[0 0.5])
>> set(H1,'Color','m')
>> text(specs(1) + 0.1,0.4,'LSL');
>> H2=line([specs(2) specs(2)],[0 0.5])
>> set(H2,'Color','m')
>> text(specs(2) + 0.1, 0.4,'USL');
>> grid on
Пример смещенного вправо параметра технологического процесса с границами рассеяния параметра совпадающими с границами допусков. Номинальное значение параметра равно нулю.
>> data=normrnd(1.5,1,100,1);
>> specs=[-3 3];
>> [p,Cp,Cpk] = capable(data,specs)
p =
0.0945
Cp =
0.8797
Cpk =
0.4380
Графическое представление смещенного вправо параметра технологического процесса и границами рассеяния параметра совпадающими с границами допусков.
>> data=normrnd(1.5,1,100,1);
>> specs=[-3 3];
>> capaplot(data,specs)
>> H = line([0 0],[0 0.4])
>> set(H,'LineWidth',3, 'Color','k')
>> H0 = line([mean(data) mean(data)],[0 0.4])
>> set(H0,'LineWidth',3, 'Color','b')
>> H1=line([specs(1) specs(1)],[0 0.4])
>> set(H1,'Color','m')
>> text(specs(1) + 0.1,0.4,'LSL');
>> H2=line([specs(2) specs(2)],[0 0.4])
>> set(H2,'Color','m')
>> text(specs(2) + 0.1, 0.4,'USL');
>> grid on
capaplot - График воспроизводимости процесса
Синтаксис
p = capaplot(data,specs)
[p,h] = capaplot(data,specs)
Описание
p = capaplot(data,specs) позволяет построить график функции плотности нормального закона по точечным оценкам математического ожидания и среднего квадратического отклонения выборки data с наложенными границами допусков параметра specs. Выборка входных значений data должна быть представлена как вектор. Предполагаемся, что выборка data не противоречит нормальному закону. Выходной параметр p является вероятностью попадания значения случайной величины в границы допусков specs. Границы допусков задаются в виде двухэлементного вектора: specs(1) - нижняя граница допуска, specs(2) - верхняя граница допуска. Вероятность попадания значений параметра технологического процесса на графике представляется закрашенной областью между границами допусков specs, осью абсцисс и кривой функции плотности распределения вероятности нормального закона.
[p,h] = capaplot(data,specs) функция кроме величины p возвращает массив указателей на элементы графика воспроизводимости h.
Примеры использования функции построения графика воспроизводимости процесса
Пример несмещенного технологического процесса с нулевым математическим ожиданием и единичной дисперсией. Нижняя и верхняя границы допусков равны LSL=-2; USL=2.
>> data = normrnd(0,1,50,1);
>> p = capaplot(data,[-2 2])
p =
0.9530
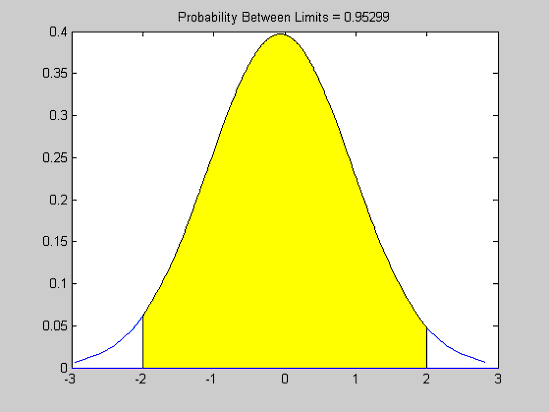
Пример смещенного технологического процесса с единичным математическим ожиданием и единичной дисперсией. Нижняя и верхняя границы допусков равны LSL=-2; USL=2.
>> data = normrnd(1,1,50,1);
>> p = capaplot(data,[-2 2])
p =
0.8464
Использование функции capaplot для получения указателей на элементы графика воспроизводимости. Процесс несмещенный с нулевым математическим ожиданием и единичной дисперсией. Нижняя и верхняя границы допусков равны LSL=-2; USL=2.
>> data = normrnd(1,1,50,1);
>> [p h] = capaplot(data,[-2 2])
p =
0.8163
h =
129.0002
3.0046
102.0051
>> h(1)
ans =
129.0002
>> get(h(1))
Color = [0 0 1]
EraseMode = normal
LineStyle = -
LineWidth = [0.5]
Marker = none
MarkerSize = [6]
MarkerEdgeColor = auto
MarkerFaceColor = none
XData = [ (1 by 250) double array]
YData = [ (1 by 250) double array]
ZData = []
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [101.001]
Selected = off
SelectionHighlight = on
Tag =
Type = line
UIContextMenu = []
UserData = []
Visible = on
ewmaplot - Контрольная карта экспоненциально взвешенного среднего
Синтаксис
ewmaplot(data)
ewmaplot(data,lambda)
ewmaplot(data,lambda,alpha)
ewmaplot(data,lambda,alpha,specs)
h = ewmaplot(...)
Описание
ewmaplot(data) функция предназначена для построения контрольной карты экспоненциально взвешенного скользящего среднего для выборки data. Размерность матрицы DATA равна n×m, где n - количество выборок (строк DATA), m - объем выборки (число столбцов DATA). Последовательность выборок (строк матрицы data) должна соответствовать порядку сбора исходных данных. На графике контрольной карты отображаются выборочное скользящее среднее ![]() , i=1..n, центральная линия, соответствующая общему среднему
, i=1..n, центральная линия, соответствующая общему среднему ![]() , верхняя UCL и нижняя LCL контрольные границы.
, верхняя UCL и нижняя LCL контрольные границы.
Верхняя и нижняя контрольные границы определяются как
![]() ,
, ![]() ,
,
![]() - среднее квадратическое отклонение
- среднее квадратическое отклонение ![]() .
.
ewmaplot(data,lambda) функция служит для построения контрольной карты экспоненциально взвешенного скользящего среднего для выборки data и переменной lambda, отвечающей за степень влияния предыдущих значений на текущее скользящее среднее. Большее значение lambda соответствует большему весу предыдущих наблюдений. Величина lambda должна находиться в интервале [0 1]. По умолчанию lambda=0.4.
ewmaplot(data,lambda,alpha) функция позволяет построить контрольную карту экспоненциально взвешенного скользящего среднего для выборки data с заданным весом предыдущих наблюдений lambda и уровнем значимости alpha для верхней и нижней контрольных границ. По умолчанию alpha=0,0027, это соответствует ± 3![]() :
:
>> norminv(1-0.0027/2)
ans =
3.0000
Для расчета уровня значимости alpha соответствующего ± k средних квадратических отклонений скользящего среднего используется выражение 2*(1-normcdf(k)). Например, для k=2 значение conf равно
>> k = 2;
>> alpha =2*(1-normcdf(k))
alpha =
0.0455
ewmaplot(data,lambda,alpha,specs) функция служит для построения контрольной карты экспоненциально взвешенного скользящего среднего для выборки data с заданным весом предыдущих наблюдений lambda, уровнем значимости alpha и границ допуска параметра specs. Границы допусков определяются как вектор с двумя элементами: specs(1) - нижняя граница допуска, specs(2) - верхняя граница допуска.
h = ewmaplot(...) в этом варианте синтаксиса допустимы любые перечисленные выше входные параметры, выходным параметром h является вектор указателей на объекты графика контрольной карты.
Примеры использования функции построения контрольной карты экспоненциально взвешенного скользящего среднего
EWMA контрольная карта для технологического процесса с постоянным нулевым математическим ожиданием и единичной дисперсией.
>>data=normrnd(0,1,20,5)
data =
0.4634 1.4766 0.6970 -0.5102 -0.5608
-0.9241 -0.8138 -1.3664 -0.0067 0.1793
-0.6497 0.6450 0.3630 -0.5255 -0.7715
0.6229 -1.3099 -0.5670 0.7177 -0.9434
-1.3351 -0.8674 -1.0442 1.0884 -1.4076
1.0477 -0.4742 0.6971 0.5006 -1.9061
0.8633 0.2224 0.4840 2.7718 -0.0653
-0.6424 1.8713 -0.1938 -0.1603 0.6721
0.6600 0.1100 -0.3781 0.4295 0.2061
1.2941 -0.4113 -0.8864 -1.9668 -0.0081
0.3146 0.5112 -1.8402 -0.5460 0.0200
0.8596 -1.1991 -1.6282 -1.8884 -0.5584
0.1287 -0.0964 -1.1738 -0.1080 1.8861
0.0166 0.4458 -0.4154 -1.3161 -0.2200
-0.0728 -0.2958 0.1751 -0.6726 -1.4144
-0.9943 -0.1680 0.2294 -0.9024 -0.3028
-0.7474 0.1795 -1.2409 -0.1548 -0.5696
-0.0308 0.4211 0.7000 0.9472 -0.1215
0.9884 1.6777 0.4269 1.5504 -0.3902
-0.5990 1.9969 1.4548 0.4290 -0.8443
>>ewmaplot(data)
Вид EWMA контрольной карты для технологического процесса с постоянным нулевым математическим ожиданием, единичной дисперсией и коэффициентом влияния lambda=[0.1 0.3 0.6 1].
>>data=normrnd(0,1,20,5);
>>lambda=0.1;
>> subplot(2,2,1)
>>ewmaplot(data,lambda)
>>lambda=0.3;
>> subplot(2,2,2)
>>ewmaplot(data,lambda)
>>lambda=0.6;
>> subplot(2,2,3)
>>ewmaplot(data,lambda)
>>lambda=1;
>> subplot(2,2,4)
>>ewmaplot(data,lambda)
EWMA контрольная карта для контрольных границ на уровне ±2,5![]() .
.
>>data=normrnd(0,1,20,5);
>>lambda=0.5;
>> k = 2.5;
>> alpha =2*(1-normcdf(k))
alpha =
0.0124
>> ewmaplot(data,lambda,alpha)
EWMA контрольная карта для технологического процесса с линейно нарастающим математическим ожиданием, равным 10+0.02*t(:,ones(4,1)) при t = (1:28)', постоянной дисперсией, равной 0,52. Выборка исходных данных data является матрицей с размерностью 28×4, где количество выборок равно 28, число измерений в выборке - 4. Контрольная карта экспоненциально взвешенного скользящего среднего строиться для постоянной сглаживания lambda =0.4, контрольных границ соответствующих уровню значимости alpha =0.01. Границы допусков параметра равны LSL=9,75; USL=10,75.
>> t = (1:28)';
>> data = normrnd(10+0.02*t(:,ones(4,1)),0.5);
>> lambda =0.4;
>> alpha =0.01;
>> specs=[9.75 10.75];
>> ewmaplot(data, lambda, alpha, specs)
Получение доступа к свойствам объектов EWMA контрольной карты.
>>data=normrnd(0,1,20,5);
>>lambda=0.5;
>> alpha =0.0124;
>> h=ewmaplot(data,lambda,alpha)
h =
113.0018
3.0089
102.0116
103.0048
104.0048
105.0048
>>get(h(1))
Color = [0 0 1]
EraseMode = normal
LineStyle = -
LineWidth = [0.5]
Marker = none
MarkerSize = [6]
MarkerEdgeColor = auto
MarkerFaceColor = none
XData = [ (1 by 20) double array]
YData = [ (1 by 20) double array]
ZData = []
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [101.002]
Selected = off
SelectionHighlight = on
Tag =
Type = line
UIContextMenu = []
UserData = []
Visible = on
histfit - Гистограмма по негруппированным экспериментальным данным с наложенной на нее кривой функции плотности распределения нормального закона
Синтаксис
histfit(data)
histfit(data,nbins)
h = histfit(data,nbins)
Описание
histfit(data,nbins) функция позволяет построить гистограмму с наложенной функцией плотности вероятности нормального закона по выборке data с числом интервалов nbins. Выборка data должна быть задана как вектор негруппированных значений. Группировка выборки data выполняется по интервалам равной длины. Если параметр nbins не задан, он принимается равным ближайшему целому из корня квадратного числа элементов в выборке data.
h = histfit(data,nbins) в качестве выходного параметра выступает вектор указателей на элементы графика. Первый элемент вектора h(1) является указателем на гистограмму, h(2) - указатель на кривую плотности вероятности нормального закона.
Примеры использования функции гистограммы с графиком функции плотности нормального закона
Гистограмма с наложенным графиком функции плотности распределения вероятностей нормального закона. Число интервалов группирования определяется по умолчанию, как ближайшее целое к корню квадратному из объема выборки.
>>data=normrnd(0,1,100,1);
>>histfit(data)
Вид получаемых графиков в зависимости от объема выборки при одинаковых параметрах генерируемой выборки.
>>data=normrnd(0,1,25,1);
>>subplot(2,2,1)
>>histfit(data)
>>data=normrnd(0,1,49,1);
>>subplot(2,2,2)
>>histfit(data)
>>data=normrnd(0,1,81,1);
>>subplot(2,2,3)
>>histfit(data)
>>data=normrnd(0,1,144,1);
>>subplot(2,2,4)
>>histfit(data)
Гистограмма с наложенным графиком функции плотности распределения вероятностей нормального закона с заданным числом интервалов группирования.
>>data=normrnd(0,1,100,1);
>>nbins=7;
>>histfit(data,nbins)
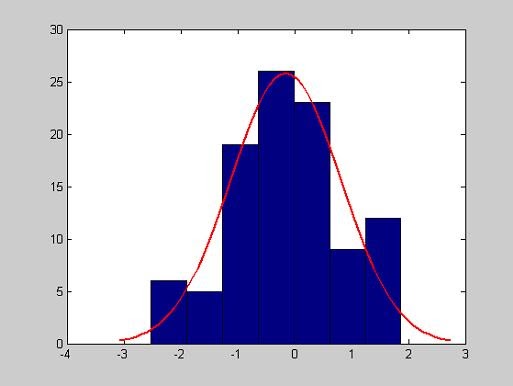
Использование указателей на элементы графика и получение списка свойств гистограммы.
>>data=normrnd(0,1,100,1);
>>nbins=7;
>>h=histfit(data,nbins)
h =
101.0029
102.0010
>>get(h(1))
AlphaDataMapping = scaled
CData = [ (4 by 7) double array]
CDataMapping = scaled
FaceVertexAlphaData = []
FaceVertexCData = [ (36 by 1) double array]
EdgeAlpha = [1]
EdgeColor = [0 0 0]
EraseMode = normal
FaceAlpha = [1]
FaceColor = flat
Faces = [ (7 by 4) double array]
LineStyle = -
LineWidth = [0.5]
Marker = none
MarkerEdgeColor = auto
MarkerFaceColor = none
MarkerSize = [6]
Vertices = [ (36 by 2) double array]
XData = [ (4 by 7) double array]
YData = [ (4 by 7) double array]
ZData = []
FaceLighting = flat
EdgeLighting = none
BackFaceLighting = reverselit
AmbientStrength = [0.3]
DiffuseStrength = [0.6]
SpecularStrength = [0.9]
SpecularExponent = [10]
SpecularColorReflectance = [1]
VertexNormals = [ (36 by 3) double array]
NormalMode = auto
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [100.001]
Selected = off
SelectionHighlight = on
Tag =
Type = patch
UIContextMenu = []
UserData = []
Visible = on
normspec - График функции плотности нормального закона с наложенными границами допусков контролируемого параметра
Синтаксис
p = normspec(specs,mu,sigma)
[p,h] = normspec(specs,mu,sigma)
Описание
p = normspec(specs,mu,sigma) функция предназначения для построения графика плотности распределения вероятностей нормального закона с заданными параметрами: математическим ожиданием mu, средним квадратическим отклонением sigma, и границами допусков параметра specs. Границы допусков определяются как вектор с двумя элементами: specs(1) - нижняя граница допуска, specs(2) - верхняя граница допуска. Выходной параметр p - вероятность попадания значения параметра в границы допусков specs. Если допуск на параметр является односторонним, то отсутствующая граница допуска задается как бесконечное значение. При одностороннем ограничении слева правая граница задается как Inf, т.е. specs(1)=A, specs(2)=Inf, или specs=[A Inf], где А - нижняя граница допуска. При одностороннем ограничении справа левая граница задается как -Inf, т.е. specs(1)=-Inf, specs(2)=В, или specs=[-Inf В], где В - верхняя граница допуска.
[p,h] = normspec(specs,mu,sigma) в этом варианте синтаксиса кроме вероятности попадания значения параметра в границы допусков p, возвращается вектор указателей элементов графика h.
Примеры использования функции графика плотности распределения вероятностей нормального закона с границами допусков параметра
График плотности распределения вероятностей несмещенного нормального технологического процесса
с двусторонними границами допусков на параметр и единичной дисперсией.
>> mu = 0;
>> sigma = 1;
>> specs = [-2 2];
>> p = normspec(specs,mu,sigma)
p =
0.9545
График плотности распределения вероятностей смещенного нормального технологического процесса
с двусторонними границами допусков на параметр и единичной дисперсией.
>> mu = 1;
>> sigma = 1;
>> specs = [-2 2];
>> p = normspec(specs,mu,sigma)
Графики плотности распределения вероятностей несмещенного нормального технологического процесса
с односторонними границами допусков на параметр и единичной дисперсией.
>> mu = 0;
>> sigma = 1;
>> specs = [-2 Inf];
>>subplot(2,1,1)
>> p = normspec(specs,mu,sigma)
p =
0.9772
>> p = normspec(specs,mu,sigma)
p =
0.9772
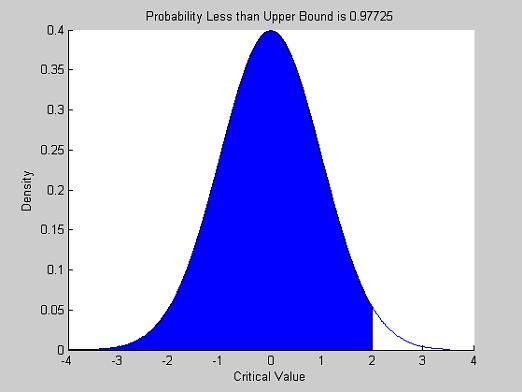
Использование указателей на элементы графика и получение списка свойств.
>> mu = 0;
>> sigma = 1;
>> specs = [-2 2];
>> [p h] = normspec(specs,mu,sigma)
p =
0.9545
h =
206.0006
207.0005
208.0005
>>get(h(1))
Color = [0 0 1]
EraseMode = normal
LineStyle = -
LineWidth = [0.5]
Marker = none
MarkerSize = [6]
MarkerEdgeColor = auto
MarkerFaceColor = none
XData = [ (1 by 2500) double array]
YData = [ (1 by 2500) double array]
ZData = []
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [205]
Selected = off
SelectionHighlight = on
Tag =
Type = line
UIContextMenu = []
UserData = []
Visible = on
schart - Контрольная карта среднего квадратического отклонения
Синтаксис
schart(DATA,conf)
schart(DATA,conf,specs)
schart(DATA,conf,specs)
[outliers,h] = schart(DATA,conf,specs)
Описание
schart(data) функция позволяет получить контрольную карту средних квадратических отклонений выборочных значений DATA. Размерность матрицы DATA равна n?m, где n - количество выборок (строк DATA), m - объем выборки (число столбцов DATA). Последовательность выборок должна соответствовать порядку сбора исходных данных. На графике контрольной карты отображаются выборочные средние квадратические отклонения (si, i=1..n), центральная линия (![]() ), верхняя UCL и нижняя LCL контрольные границы.
), верхняя UCL и нижняя LCL контрольные границы.
Среднее арифметическое выборочных средних квадратических отклонений рассчитывается по формуле:
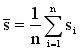
Верхняя и нижняя контрольные границы рассчитываются по формулам
![]()
![]() - среднее квадратическое отклонение
- среднее квадратическое отклонение ![]()
Если технологический процесс является статистически управляемым, то при 1000 выборках количество точек вышедших за контрольные пределы не должно превышать 3-х в случайном порядке. Таким образом, при малом количестве выборок выход выборочного среднего квадратического отклонения за контрольные границы означает потерю процессом статистической управляемости.
schart(DATA,conf) функция предназначена для построения s контрольной карты выборки DATA с заданной доверительной вероятностью conf для верхней и нижней контрольных границ. По умолчанию значение conf принимается равной 0.9973. Величина conf=0.9973 соответствует интервалу ±3![]()
>> norminv(1 - (1-.9973)/2)
ans =
3.0000
Для расчета доверительной вероятности conf соответствующей ±k![]() используется выражение 1-2*(1-normcdf(k)). Например, для k=2 значение conf равно
используется выражение 1-2*(1-normcdf(k)). Например, для k=2 значение conf равно
>> k = 2;
>> conf =1-2*(1-normcdf(k))
conf =
0.9545
schart(DATA,conf,specs) функция предназначена для построения s контрольной карты с заданной доверительной вероятностью расположения контрольных границ conf и границами допусков specs. Границы допусков определяются как вектор с двумя элементами: specs(1) - нижняя граница допуска, specs(2) - верхняя граница допуска.
[outliers,h] = schart(data,conf,specs) выходными параметрами функции являются: outlier - вектор номеров выборок (строк матрицы DATA), средние квадратические отклонения которых вышли за контрольные границы, h - вектор указателей на объекты графика контрольной карты.
Примеры использования функции построения контрольной карты средних квадратических отклонений
s контрольная карта
>>DATA=normrnd(0,1,20,5)
DATA =
-0.4326 0.2944 -1.6041 0.0000 0.6232
-1.6656 -1.3362 0.2573 -0.3179 0.7990
0.1253 0.7143 -1.0565 1.0950 0.9409
0.2877 1.6236 1.4151 -1.8740 -0.9921
-1.1465 -0.6918 -0.8051 0.4282 0.2120
1.1909 0.8580 0.5287 0.8956 0.2379
1.1892 1.2540 0.2193 0.7310 -1.0078
-0.0376 -1.5937 -0.9219 0.5779 -0.7420
0.3273 -1.4410 -2.1707 0.0403 1.0823
0.1746 0.5711 -0.0592 0.6771 -0.1315
-0.1867 -0.3999 -1.0106 0.5689 0.3899
0.7258 0.6900 0.6145 -0.2556 0.0880
-0.5883 0.8156 0.5077 -0.3775 -0.6355
2.1832 0.7119 1.6924 -0.2959 -0.5596
-0.1364 1.2902 0.5913 -1.4751 0.4437
0.1139 0.6686 -0.6436 -0.2340 -0.9499
1.0668 1.1908 0.3803 0.1184 0.7812
0.0593 -1.2025 -1.0091 0.3148 0.5690
-0.0956 -0.0198 -0.0195 1.4435 -0.8217
-0.8323 -0.1567 -0.0482 -0.3510 -0.2656
>> schart(DATA)
s контрольная карта для контрольных границ равных ±2,5![]()
>>DATA=normrnd(0,1,20,10);
>> k = 2.5;
>> conf =1-2*(1-normcdf(k))
conf =
0.9876
>> schart(DATA,conf)
s контрольная карта для контрольных границ равных ±2![]() и границами допусков LSL=0,2; USL=1,5.
и границами допусков LSL=0,2; USL=1,5.
>> DATA=normrnd(0,1,20,10);
>> k=2;
>> conf =1-2*(1-normcdf(k));
>> specs=[0.2 1.5];
>> schart (DATA,conf,specs)
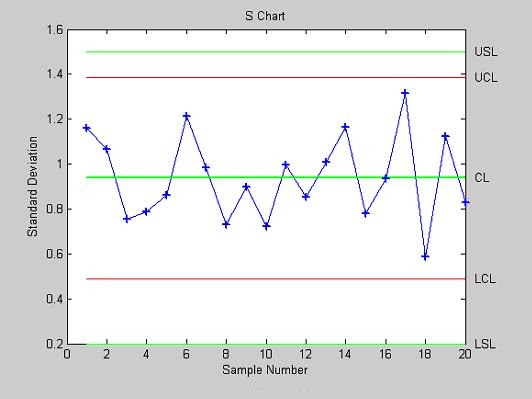
s контрольная карта для контрольных границ равных ±1,5![]() и границами допусков LSL=0,2; USL=1,5. В качестве выходных параметров выступают вектор номеров выборок вышедших за контрольные границы - outlier, и вектор указателей на объекты графика - h.
и границами допусков LSL=0,2; USL=1,5. В качестве выходных параметров выступают вектор номеров выборок вышедших за контрольные границы - outlier, и вектор указателей на объекты графика - h.
>> DATA=normrnd(0,1,20,10);
>> k=1.5;
>> conf =1-2*(1-normcdf(k));
>> specs=[0.2 1.5];
>> [outlier,h] = schart (DATA,conf,specs)
outlier =
9
h =
3.0027
102.0040
103.0016
104.0016
105.0016
106.0010
114.0007
115.0006
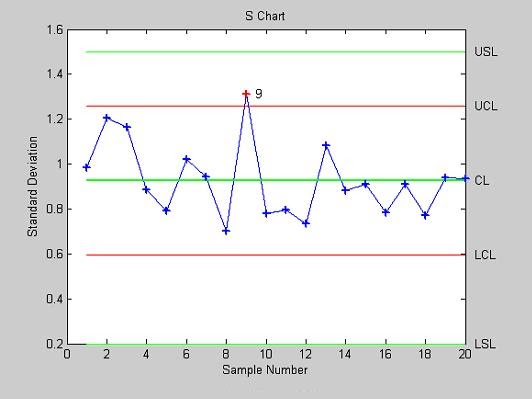
xbarplot - Контрольная карта среднего арифметического
Синтаксис
xbarplot(DATA)
xbarplot(DATA,conf)
xbarplot(DATA,conf,specs)
xbarplot(DATA,conf,specs,'sigmaest')
[outlier,h] = xbarplot(...)
Описание
xbarplot(DATA) функция позволяет получить контрольную карту средних арифметических значений (![]() ) для выборки DATA. Размерность матрицы DATA равна nxm, где n - количество выборок (строк DATA), m - объем выборки (число столбцов DATA). Последовательность выборок должна соответствовать порядку сбора исходных данных. На графике контрольной карты отображаются выборочные средние значения
) для выборки DATA. Размерность матрицы DATA равна nxm, где n - количество выборок (строк DATA), m - объем выборки (число столбцов DATA). Последовательность выборок должна соответствовать порядку сбора исходных данных. На графике контрольной карты отображаются выборочные средние значения ![]() , i=1..n, центральная линия, соответствующая общему среднему арифметическому
, i=1..n, центральная линия, соответствующая общему среднему арифметическому ![]() , верхняя UCL и нижняя LCL контрольные границы.
, верхняя UCL и нижняя LCL контрольные границы.
Общее среднее арифметическое рассчитывается по формуле:
![]() .
.
Верхняя и нижняя контрольные границы определяются как
![]() ,
, ![]() ,
,
![]() - среднее квадратическое отклонение
- среднее квадратическое отклонение ![]() .
.
Если технологический процесс является статистически управляемым, то при 1000 выборках количество точек вышедших за контрольные пределы не должно превышать 3-х в случайном порядке. Таким образом, при малом количестве выборок выход выборочного среднего арифметического ![]() за контрольные границы означает потерю процессом статистической управляемости.
за контрольные границы означает потерю процессом статистической управляемости.
xbarplot(DATA,conf) функция предназначена для построения ![]() контрольной карты для выборки DATA с заданной доверительной вероятностью conf для верхней и нижней контрольных границ. По умолчанию значение conf принимается равной 0.9973. Величина conf=0.9973 соответствует интервалу ± 3 средних квадратических отклонений общего среднего:
контрольной карты для выборки DATA с заданной доверительной вероятностью conf для верхней и нижней контрольных границ. По умолчанию значение conf принимается равной 0.9973. Величина conf=0.9973 соответствует интервалу ± 3 средних квадратических отклонений общего среднего:
>> norminv(1 - (1-.9973)/2)
ans =
3.0000
Для расчета доверительной вероятности conf соответствующей ![]() используется выражение 1-2*(1-normcdf(k)). Например, для k=2 значение conf равно
используется выражение 1-2*(1-normcdf(k)). Например, для k=2 значение conf равно
>> k = 2;
>> conf =1-2*(1-normcdf(k))
conf =
0.9545
xbarplot(DATA,conf,specs) функция предназначена для построения контрольной карты средних арифметических значений с заданной доверительной вероятностью расположения контрольных границ conf и границами допусков на параметр технологического процесса specs. Границы допусков определяются как вектор с двумя элементами: specs(1) - нижняя граница допуска, specs(2) - верхняя граница допуска.
xbarplot(DATA,conf,specs,'sigmaest') позволяет получить ![]() контрольную карту с заданной доверительной вероятностью conf. Строковый параметр 'sigmaest' служит для определения способа расчета точечной оценки стандартного отклонения общего среднего. Возможны следующие способы расчета
контрольную карту с заданной доверительной вероятностью conf. Строковый параметр 'sigmaest' служит для определения способа расчета точечной оценки стандартного отклонения общего среднего. Возможны следующие способы расчета ![]() :
:
|
Значение 'sigmaest' |
Способ расчета точечной оценки стандартного отклонения |
|
'range', 'r' |
Для расчета точечной оценки |
|
'variance', 'v' |
Точечная оценка |
|
's' |
Точечная оценка |
[outlier,h] = xbarplot(DATA,conf,specs) выходными параметрами функции являются: outlier - вектор номеров выборок (строк матрицы DATA), средние арифметические значения которых вышли за контрольные границы, h - вектор указателей на объекты графика контрольной карты.
Примеры использования функции построения контрольной карты средних арифметических значений
![]() контрольная карта
контрольная карта
>>DATA=normrnd(0,1,20,4)
DATA =
-0.4326 0.2944 -1.6041 0.0000
-1.6656 -1.3362 0.2573 -0.3179
0.1253 0.7143 -1.0565 1.0950
0.2877 1.6236 1.4151 -1.8740
-1.1465 -0.6918 -0.8051 0.4282
1.1909 0.8580 0.5287 0.8956
1.1892 1.2540 0.2193 0.7310
-0.0376 -1.5937 -0.9219 0.5779
0.3273 -1.4410 -2.1707 0.0403
0.1746 0.5711 -0.0592 0.6771
-0.1867 -0.3999 -1.0106 0.5689
0.7258 0.6900 0.6145 -0.2556
-0.5883 0.8156 0.5077 -0.3775
2.1832 0.7119 1.6924 -0.2959
-0.1364 1.2902 0.5913 -1.4751
0.1139 0.6686 -0.6436 -0.2340
1.0668 1.1908 0.3803 0.1184
0.0593 -1.2025 -1.0091 0.3148
-0.0956 -0.0198 -0.0195 1.4435
-0.8323 -0.1567 -0.0482 -0.3510
>>xbarplot(DATA)
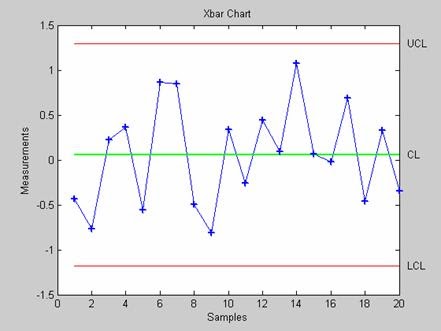
![]() контрольная карта с контрольными границами равными ±2,5
контрольная карта с контрольными границами равными ±2,5![]()
>>DATA=normrnd(0,1,20,4);
>> k = 2.5;
>> conf =1-2*(1-normcdf(k))
conf =
0.9876
>> xbarplot(DATA,conf)
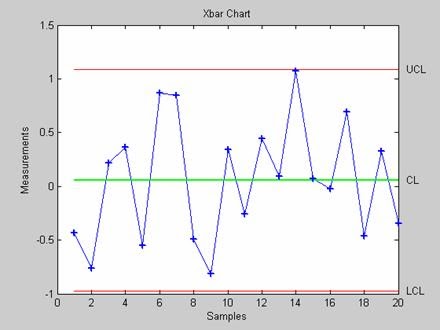
![]() контрольная карта с контрольными границами равными ±2
контрольная карта с контрольными границами равными ±2![]() и границами допусков технологического параметра -1; 1.
и границами допусков технологического параметра -1; 1.
>> DATA=normrnd(0,1,20,4);
>> k=2;
>> conf =1-2*(1-normcdf(k));
>> specs=[-1 1];
>> xbarplot(DATA,conf,specs)
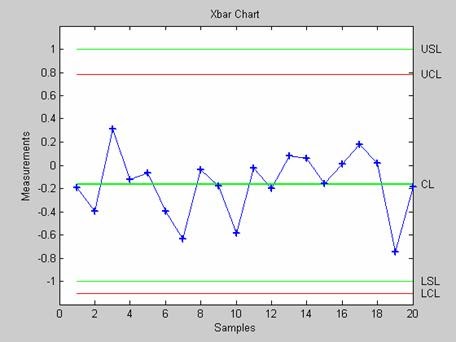
![]() контрольная карта с контрольными границами равными ±2
контрольная карта с контрольными границами равными ±2![]() . Для расчета точечной оценки стандартного отклонения
. Для расчета точечной оценки стандартного отклонения ![]() используется средний выборочный размах.
используется средний выборочный размах.
>> DATA=normrnd(0,1,20,4);
>> k=2;
>> conf =1-2*(1-normcdf(k));
>> specs=[-1 1];
>> sigmaest='range';
>> xbarplot(DATA,conf,specs,sigmaest)
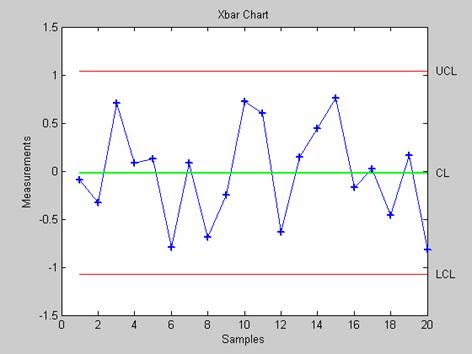
Следует отметить, в этом варранте синтаксиса функции xbarplot не предусмотрено построение границ допусков на технологический параметр. Согласно тексту файла xbarplot.m границы допусков будут построены только при 3-х входных параметрах.
![]() контрольная карта с контрольными границами равными ±1,5
контрольная карта с контрольными границами равными ±1,5![]() и границами допусков технологического параметра в интервале -1; 1. В качестве выходных параметров выступают вектор номеров выборок вышедших за контрольные границы - outlier, и вектор указателей объектов графика - h.
и границами допусков технологического параметра в интервале -1; 1. В качестве выходных параметров выступают вектор номеров выборок вышедших за контрольные границы - outlier, и вектор указателей объектов графика - h.
>> DATA=normrnd(0,1,20,4);
>> k=1.5;
>> conf =1-2*(1-normcdf(k));
>> specs=[-1 1];
>> [outlier,h] = xbarplot(DATA,conf,specs)
outlier =
7
9
11
12
13
14
17
19
h =
3.0027
102.0040
103.0016
104.0016
105.0016
106.0010
121.0004
122.0004
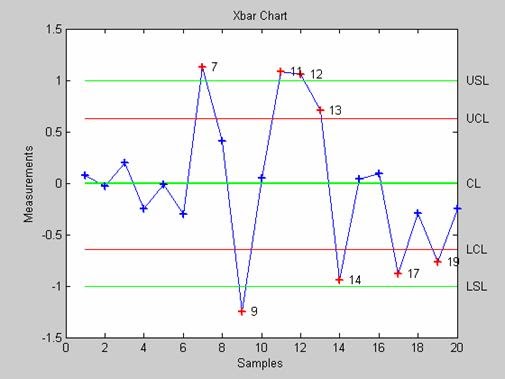
anova1 - Однофакторный дисперсионный анализ
Синтаксис
p = anova1(X)
p = anova1(X,group)
p = anova1(X,group,'displayopt')
[p,table] = anova1(...)
[p,table,stats] = anova1(...)
Описание
p = anova1(X) функция позволяет провести однофакторный дисперсионный анализ для сравнения средних арифметических значений одной или нескольких выборок одинакового объема. Выборки определяются входным аргументом Х. Х задается как матрица с размерностью mxn, где m - число наблюдений в выборке (число строк Х), n - количество выборок (число столбцов матрицы Х). Выборки должны быть независимыми. Выходным аргументом функции является уровень значимости p нулевой гипотезы. Нулевая гипотеза состоит в том, что все выборки в матрице Х взяты из одной генеральной совокупности или из разных генеральных совокупностей с равными средними арифметическими. p является вероятностью ошибки первого рода, или вероятностью необоснованно отвергнуть нулевую гипотезу. Если значение p![]() 0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выбор критического уровня значимости pKP для условия принятия нулевой гипотезы
0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выбор критического уровня значимости pKP для условия принятия нулевой гипотезы
![]()
предоставлен исследователю. В большинстве практических случаев pKP принимают равным 0,05; 0,01.
При проведении дисперсионного анализа общая дисперсия делится на две составляющие:
-
межгрупповую дисперсию - дисперсию средних арифметических значений выборок матрицы Х относительно общего среднего;
-
внутригрупповую дисперсию - дисперсию значений выборок относительно выборочных средних.
Результаты расчета отображаются в двух графических окнах. В первое окно выводится таблица с результатами однофакторного дисперсионного анализа, во втрое - диаграмма размаха для средних арифметических по заданным выборкам.
Таблица с результатами однофакторного дисперсионного анализа содержит 6 столбцов (рис. 1):
-
вид дисперсии (Source):
-
внутригрупповая (Columns),
-
межгрупповая (Error),
-
общая (Total);
-
-
сумму квадратов разностей (SS) между средним арифметическим и значениями выборки по каждому виду дисперсии;
-
число степеней свободы по каждому виду дисперсии (df);
-
среднее значение суммы квадратов разностей (MS) по каждому виду дисперсии, определяемое как отношение SS/df;
-
значение статистики Фишера (F статистики) для MS;
-
значение уровня значимости p (Prob>F) для рассчитанного значения статистики F. Если величина F увеличивается, то значение p должно уменьшаться.
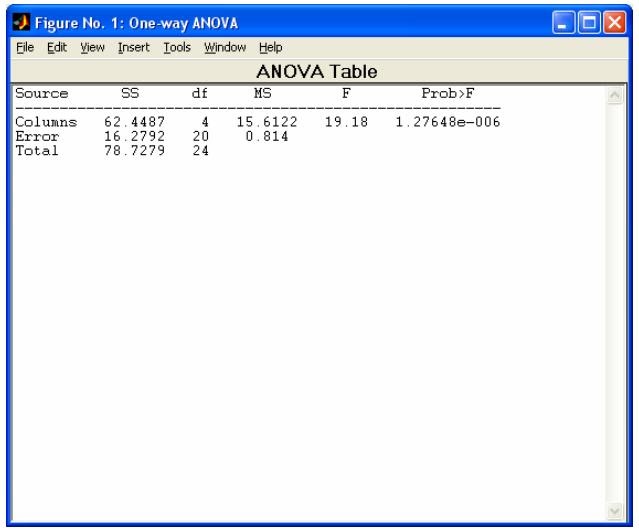
Рис. 1. Таблица однофакторного дисперсионного анализа.
Диаграмма размаха средних арифметических значений строится по выборкам, т.е. по столбцам матрицы Х, и является аналогом диаграммы размаха для медиан выборок, получаемой при помощи функции boxplot. Чем больше разница между центральными линиями на диаграмме размаха (средними арифметическими выборок), тем больше разница между выборочными значениями статистики F и меньше соответствующие значения уровня значимости p.
p = anova1(X,group) входной аргумент group задает метки выборок Х и названий соответствующих им графиков на диаграмме размаха. Метки выборок group задаются вектором строк или массивом ячеек. Число элементов вектора group должно быть равно количеству столбцов матрицы Х.
Выборки могут быть заданы как вектор Х. Деление элементов Х на выборки выполняется при помощи входного аргумента group. group может быть задан вектор, символьный массив (вектор строк) или массив ячеек. Принадлежность элемента вектора Х к выборке определяется одинаковым значением соответствующего элемента вектора group. Размерность векторов Х и group должна совпадать. Значения вектора group являются метками соответствующих графиков выборок на диаграмме размаха средних арифметических.
Векторная форма задания выборок Х по группирующей переменной group позволяет проводить однофакторный дисперсионный анализ по выборкам неодинакового объема. Если элемент вектора группирующей переменной groupi содержит пустую строку, пустую ячейку массива или нечисловое значение NaN, то соответствующий элемент данных в векторе Х игнорируется при расчете.
p = anova1(X,group,'displayopt') входной аргумент 'displayopt' позволяет явно задать отображение графических окон с таблицей результатов дисперсионного анализа и диаграммой размаха 'displayopt'='on', или подавить вывод графических окон 'displayopt'='off'. Значение по умолчанию 'displayopt'='on'.
[p,table] = anova1(...) функция возвращает таблицу с результатами однофакторного дисперсионного анализа в текстовой форме в командное окно MATLAB.
[p,table,stats] = anova1(...) функция возвращает структуру stats используемую для проведения парных сравнений средних арифметических выборок. Проверка параметрической гипотезы о равенстве двух средних арифметических выполняется при помощи функции multcompare. Структура данных stats передается функции multcompare как входной аргумент.
Однофакторный дисперсионный анализ основан на следующих предположениях:
-
выборки распределены нормально;
-
выборки имеют одинаковую дисперсию;
-
наблюдения в выборках взаимно независимы.
Однофакторный дисперсионный анализ нечувствителен к малым отклонениям от первого и второго условий.
Примеры использования функции однофакторного дисперсионного анализа
Однофакторный дисперсионный анализ для пяти выборок с математическими ожиданиями изменяющимися
в пределах от 1 до 5.
>> X = meshgrid(1:5)
X =
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
>> X = X + normrnd(0,1,5,5)
X =
0.5674 3.1909 2.8133 4.1139 5.2944
-0.6656 3.1892 3.7258 5.0668 3.6638
1.1253 1.9624 2.4117 4.0593 5.7143
1.2877 2.3273 5.1832 3.9044 6.6236
-0.1465 2.1746 2.8636 3.1677 4.3082
>> p = anova1(X)
p =
1.2765e-006
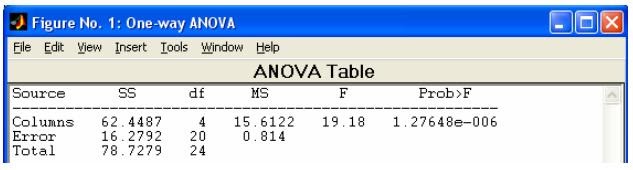
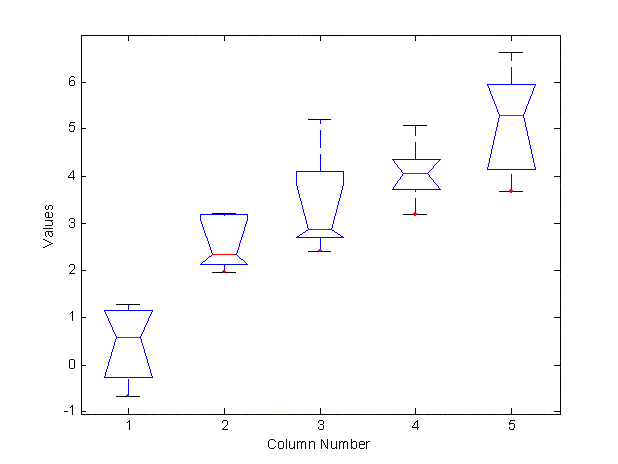
Однофакторный дисперсионный анализ для пяти выборок с математическими ожиданиями,
изменяющимися в пределах от 1 до 5. Метки выборок заданы переменной group.
>> X = meshgrid(1:5)
X =
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
>> X = X + normrnd(0,1,5,5)
X =
0.5674 3.1909 2.8133 4.1139 5.2944
-0.6656 3.1892 3.7258 5.0668 3.6638
1.1253 1.9624 2.4117 4.0593 5.7143
1.2877 2.3273 5.1832 3.9044 6.6236
-0.1465 2.1746 2.8636 3.1677 4.3082
>> group = ['Aa'; 'Bb'; 'Cc'; 'Dd'; 'Ee']
group =
Aa
Bb
Cc
Dd
Ee
>> p = anova1(X, group)
p =
1.2765e-006
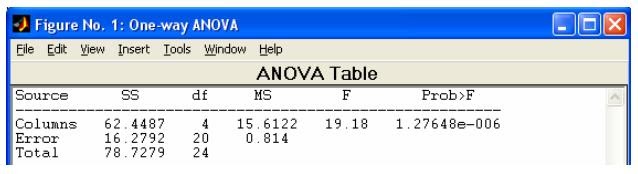
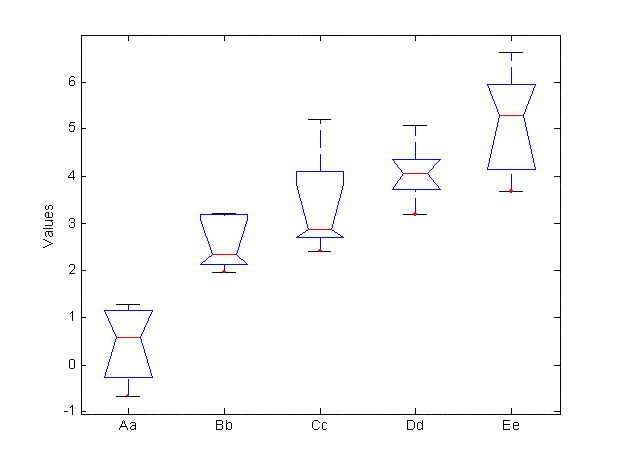
Однофакторный дисперсионный анализ для пяти выборок с переменным объемом.
Группировка значений вектора Х по выборкам выполняется вектором целых чисел group.
>> X = normrnd(0,1,104,1);
>> group = unidrnd(4,104,1);
>> p = anova1(X, group)
p =
0.5473
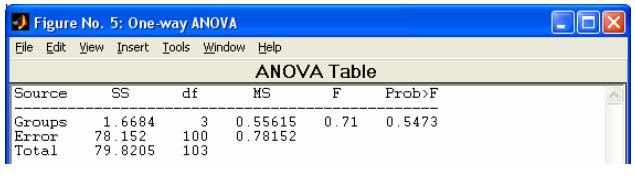
Однофакторный дисперсионный анализ для пяти выборок с математическими ожиданиями, изменяющимися в пределах от 1 до 5. Метки выборок заданы переменной group. Функция возвращает таблицу с результатами однофакторного дисперсионного анализа в текстовой форме в командное окно MATLAB. Функция anova1 возвращает структуру данных stats.
>> X = meshgrid(1:5);
>> X = X + normrnd(0,1,5,5);
>> group = ['Aa'; 'Bb'; 'Cc'; 'Dd'; 'Ee'];
>> [p,table,stats] = anova1(X, group)
p =
4.3652e-005
table =
Columns 1 through 5
'Source' 'SS' 'df' 'MS' 'F'
'Columns' [37.0002] [ 4] [9.2501] [11.8040]
'Error' [15.6728] [20] [0.7836] []
'Total' [52.6730] [24] [] []
Column 6
'Prob>F'
[4.3652e-005]
[]
[]
stats =
gnames: {5x1 cell}
n: [5 5 5 5 5]
source: 'anova1'
means: [1.1484 2.1861 3.1478 3.6339 4.7007]
df: 20
s: 0.8852
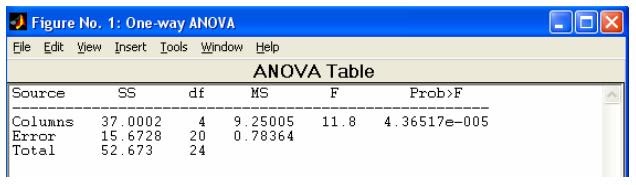
>> stats.gnames
ans =
'Aa'
'Bb'
'Cc'
'Dd'
'Ee'
anova2 - Двухфакторный дисперсионный анализ
Синтаксис
p = anova2(X,reps)
p = anova2(X,reps,'displayopt')
[p,table] = anova2(...)
[p,table,stats] = anova2(...)
Описание
anova2(X,reps) функция позволяет провести двухфакторный дисперсионный анализ для сравнения средних арифметических значений m столбцов и n строк в матрице Х. Данные в столбцах и строках соответствуют разным уровням факторов А и В. Количество повторных наблюдений для всех комбинаций уровней факторов А и В задается входным аргументов reps. Значение reps должно быть постоянным целым числом. Дисперсионный анализ для переменного числа наблюдений по уровням факторов используется функция многофакторного дисперсионного анализа anovan.
Если фактор А имеет два уровня, фактор В - три уровня и рассматриваются два наблюдения для сочетаний уровней факторов А и В (reps=2), то матрица Х примет следующий вид
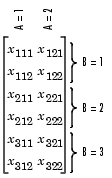
При reps=1 (значение по умолчанию) функция anova2 позволяет рассчитать вектор уровней значимости р, содержащий два элемента. Если количество повторений reps>1, anova2 возвращает вектор p с 3 элементами. Назначение элементов вектора р:
1. уровень значимости р(1) нулевой гипотезы, H0A, состоящей в том, что все выборки соответствующие уровням фактора А, т.е. все столбцы в матрице Х, извлечены из той же генеральной совокупности;
2. уровень значимости р(2) нулевой гипотезы, H0В, состоящей в том, что все выборки соответствующие уровням фактора В, т.е. все строки в матрице Х, извлечены из той же генеральной совокупности;
3. уровень значимости р нулевой гипотезы, H0АВ, состоящей в том, что отсутствует эффект взаимодействия между факторами А и В. Для reps>1.
p является вероятностью ошибки первого рода, или вероятностью необоснованно отвергнуть нулевую гипотезу. Если значение p близко к нулю, то нулевая гипотеза может быть отвергнута. р≈0 для гипотезы H0A означает, что хотя бы одно из средних арифметических, рассчитанных по столбцам, отличается от остальных значений, т.е. существует значимый главный эффект фактора А. р≈0 для гипотезы H0В означает, что хотя бы одно из средних арифметических, рассчитанных по строкам, отличается от остальных значений, т.е. существует значимый главный эффект фактора В. р≈0 для гипотезы H0АВ означает, что существует значимый эффект взаимодействия между факторами А и В.
Выбор критического уровня значимости ![]() для условия принятия нулевой гипотезы
для условия принятия нулевой гипотезы
![]() ,
,
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
При проведении дисперсионного анализа общая дисперсия делится на 3 или 4 составляющие в зависимости от значения reps:
-
дисперсия между средними арифметическими по столбцам Х (дисперсия между средними арифметическими по фактору А);
-
дисперсия между средними арифметическими по строкам Х (дисперсия между средними арифметическими по фактору В);
-
дисперсия, обусловленная взаимодействием между строками и столбцами Х (рассчитывается, если reps>1);
-
остаточная дисперсия.
Таблица с результатами двухфакторного дисперсионного анализа отображается в графическом окне и содержит 6 столбцов (рис. 1):
-
вид дисперсии (Source):
§ дисперсия между средними арифметическими по столбцам Х (Columns),
§ дисперсия между средними арифметическими по строкам Х (Rows),
§ дисперсия обусловленная взаимодействием между строками и столбцами Х (Interaction),
§ остаточная дисперсия (Error)
§ общая дисперсия (Total); -
сумму квадратов разностей (SS) между средним арифметическим и значениями выборки по каждому виду дисперсии;
-
число степеней свободы по каждому виду дисперсии (df);
-
среднее значение суммы квадратов разностей (MS) по каждому виду дисперсии, определяемое как отношение SS/df;
-
значение статистики Фишера (F статистики) для MS;
значение уровня значимости p (Prob>F) для рассчитанного значения статистики F. Если величина F увеличивается, то значение p должно уменьшаться. 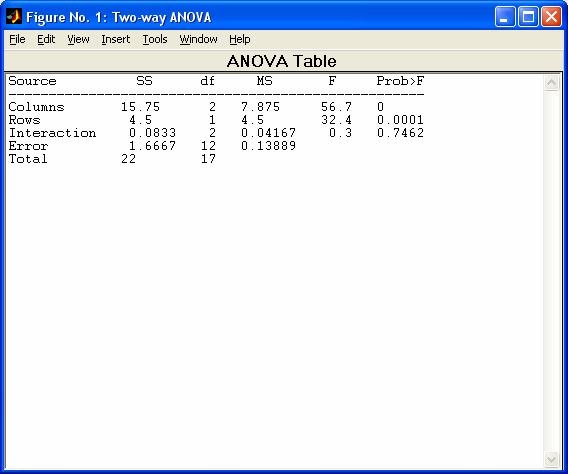
Рис. 1. Таблица двухфакторного дисперсионного анализа.
p = anova2(X,reps,'displayopt') входной аргумент 'displayopt' позволяет отобразить графическое окно с таблицей результатов дисперсионного анализа 'displayopt'='on', или подавить вывод графического окна 'displayopt'='off'. Значение по умолчанию 'displayopt'='on'.
[p,table] = anova2(...) функция возвращает таблицу с результатами двухфакторного дисперсионного анализа в текстовой форме в командное окно MATLAB.
[p,table,stats] = anova2(...) функция возвращает структуру stats используемую для проведения парных сравнений средних арифметических выборок. Проверка параметрической гипотезы о равенстве двух средних арифметических выполняется при помощи функции multcompare. Структура данных stats передается функции multcompare как входной аргумент.
Примеры использования функции двухфакторного дисперсионного анализа
Двухфакторный дисперсионный анализ для шести уровней по каждому фактору и единичному числу повторений.
>> X = unifrnd(0,1,6,6);
>> p = anova2(X,1)
p =
0.1530 0.9926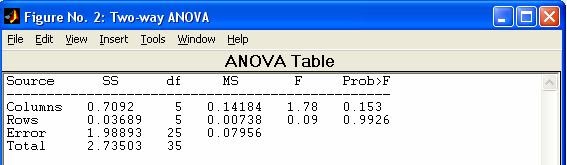
Двухфакторный дисперсионный анализ для шести уровней по первому фактору, двум уровням по второму фактору и 3-х повторений.
>> X = normrnd(0,1,6,6);
>> p = anova2(X,3)
p =
0.8380 0.9897 0.2309 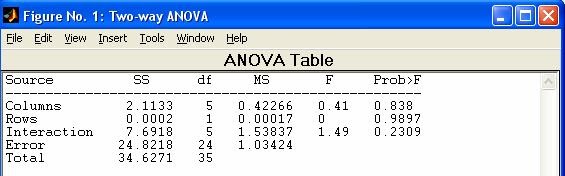
Двухфакторный дисперсионный анализ для шести уровней по первому фактору, двум уровням по второму фактору и 3-х повторений. Функция возвращает вектор уровней значимости р, таблицу двухфакторного дисперсионного анализа table, структуру stats для парных сравнений средних арифметических выборок.
>> X = normrnd(0,1,6,6);
>> [p,table,stats] = anova2(X,3)
p =
0.1751 0.4596 0.0366
table =
'Source' 'SS' 'df' 'MS' 'F' 'Prob>F'
'Columns' [ 5.2429] [ 5] [1.0486] [1.6911] [0.1751]
'Rows' [ 0.3502] [ 1] [0.3502] [0.5648] [0.4596]
'Interaction' [ 8.8611] [ 5] [1.7722] [2.8582] [0.0366]
'Error' [14.8813] [24] [0.6201] [] []
'Total' [29.3355] [35] [] [] []
stats =
source: 'anova2'
sigmasq: 0.6201
colmeans: [-0.2958 0.0404 -0.6404 0.2944 0.4974 -0.2469]
coln: 6
rowmeans: [0.0401 -0.1571]
rown: 18
inter: 1
pval: 0.0366
df: 24
anovan - Многофакторный дисперсионный анализ
Синтаксис
p = anovan(X,group)
p = anovan(X,group,'model')
p = anovan(X,group,'model',sstype)
p = anovan(X,group,'model',sstype,gnames)
p = anovan(X,group,'model',sstype,gnames,'displayopt')
[p,table] = anovan(...)
[p,table,stats] = anovan(...)
[p,table,stats,terms] = anovan(...)
Описание
p = anovan(X,group) функция позволяет провести многофакторный дисперсионный анализ для сравнения средних арифметических значений N выборок. Выборки задаются в виде вектора Х. Факторы и их уровни определяются массивом ячеек group. Каждая ячейка аргумента group содержит список уровней факторов соответствующих наблюдениям в векторе Х. Список в каждой ячейке может быть вектором, массивом символов, или массивом ячеек содержащим строковые переменные. Количество элементов group должно совпадать с числом элементов в векторе Х.
Пример задания входных аргументов: выборки X из 8 элементов и аргумента group для 3-х факторов изменяющихся на двух уровнях:
X = [x1 x2 x3 x4 x5 x6 x7 x8];
group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
Уровни первого фактора кодируются целыми числами, второго - вектором строк, третьего - списком строк. Значение x1 соответствует уровню первого фактора равного 1, второго - 'hi', третьего - 'may', и т.д.
Выходной вектор р содержит значения уровней значимости нулевой гипотезы относительно главных эффектов. Элемент p(1) является уровнем значимости нулевой гипотезы, H0A, состоящей в том, что выборки соответствующие уровням фактора А взяты из одной и той же генеральной совокупности. Элемент p(2) является уровнем значимости нулевой гипотезы, H0В, состоящей в том, что выборки соответствующие уровням фактора В взяты из одной и той же генеральной совокупности. И так далее по всем остальным элементам вектора p(i).
p является вероятностью ошибки первого рода, или вероятностью необоснованно отвергнуть нулевую гипотезу (HO). HO может быть отвергнута, если p близко к нулю. р≈0 для гипотезы H0A означает, что хотя бы одно из средних арифметических, рассчитанных по выборкам, соответствующим различным уровням фактора А, отличается от остальных значений, т.е. существует значимый главный эффект фактора А. И так далее по всем остальным факторам (элементам вектора р(i)).
Выбор критического уровня значимости ![]() для условия принятия нулевой гипотезы
для условия принятия нулевой гипотезы
![]() ,
,
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
При проведении дисперсионного анализа общая дисперсия по умолчанию делится на:
-
дисперсию, обусловленную изменениями уровней факторов для заданной модели, кодирующей оцениваемые факторы;
-
остаточная дисперсия.
Таблица с результатами многофакторного дисперсионного анализа отображается в графическом окне и содержит 6 столбцов:
-
вид дисперсии (Source):
-
сумму квадратов разностей (SS) между средним арифметическим и значениями выборки по каждому виду дисперсии;
-
число степеней свободы по каждому виду дисперсии (df);
-
среднее значение суммы квадратов разностей (MS) по каждому виду дисперсии, определяемое как отношение SS/df;
-
значение статистики Фишера (F статистики) для MS;
-
значение уровня значимости p (Prob>F) для рассчитанного значения статистики F.
p = anovan(X,group,'model') функция позволяет провести многофакторный дисперсионный анализ для заданной модели оцениваемых эффектов. Выходной вектор p содержит результаты расчета уровней значимости для нулевых гипотез относительно факторов модели. Вид модели факторов определяется входным аргументом 'model'. Предусмотрены следующие виды моделей: 'linear' - линейная модель, включающая главные эффекты; 'interaction' - модель, включающая эффекты парных взаимодействий; 'full' - полная модель, включающая главные эффекты и эффекты парных взаимодействий.
Кроме указанных строковых значений, входной аргумент 'model' может быть задан как целое число или вектор. Если входной аргумент 'model' задан как целое число k (k≤N) функция anovan позволяет оценить значимость взаимодействий факторов до k уровня. Значения k=1 и k=2 соответствуют 'model'='linear' и 'interaction' соответственно. k=N соответствует 'model'='full'.
Использование вектора целых чисел при определении 'model' позволяет оценить значимость заданных главных эффектов и эффектов взаимодействий факторов. Каждый элемент вектора 'model' кодирует в десятичной форме двоичное число, определяющее главный эффект или эффект взаимодействия. Примеры кодирования главных эффектов или эффектов взаимодействия для 3 факторов приведены в следующей таблице
|
Двоичный аналог |
Десятичный элемент вектора 'model' |
Вид эффекта при дисперсионном анализе |
|
[0 0 1] |
1 |
Главный эффект A |
|
[0 1 0] |
2 |
Главный эффект B |
|
[1 0 0] |
4 |
Главный эффект C |
|
[0 1 1] |
3 |
Эффект взаимодействия AB |
|
[1 1 0] |
6 |
Эффект взаимодействия BC |
|
[1 0 1] |
5 |
Эффект взаимодействия AC |
|
[1 1 1] |
7 |
Эффект взаимодействия ABC |
Например, если 'model'=[2 4 6] выходной вектор р содержит значения уровня значимости для проверки нулевых гипотез значимости главных эффектов В и С и эффекта взаимодействия ВС в приведенном порядке.
Одним из возможных способов задания вектора 'model' является модификация выходного параметра terms функции anovan. Вектор terms кодирует главные эффекты и эффекты взаимодействий факторов согласно формату входного аргумента 'model'. Например, если после проведения дисперсионного анализа по трем факторам для 'model'=[2 4 6] эффект взаимодействий ВС оказался статистически на значим, то для коррекции главных эффектов В и С необходимо использовать 'model'=[2 4].
p = anovan(X,group,'model',sstype) функция позволяет провести многофакторный дисперсионный анализ для заданного способа расчета суммы квадратов отклонений SS. Способ расчета суммы квадратов отклонений определяется входным аргументом sstype. Предусмотрено 3 способа расчета (sstype=1, 2, 3). Значение по умолчанию sstype=3. Способ расчета суммы квадратов отклонений влияет на результаты многофакторного дисперсионного анализа для выборок неодинакового объема.
Сумма квадратов отклонений для какого либо эффекта фактора определяется при сравнении двух составляющих. При первом способе расчета для model(i) SS является разницей остаточных сумм квадратов отклонений множества факторов model(j), где j=1..i, и текущего фактора. Второй способ расчета SS для model(i) представляет собой разность остаточной суммы квадратов отклонений главных эффектов за исключением model(i) и остаточной суммы квадратов отклонений главных эффектов с добавлением model(i). Третий способ расчета SS для model(i) представляет собой разность остаточной суммы квадратов отклонений для всех факторов в model за исключением model(i) и остаточной суммы квадратов отклонений по всем факторам в model.
Рассмотрим пример формирования сумм квадратов отклонений 1, 2, 3 типов для двух факторов А и В. Модель может содержать два главных эффекта факторов А и В и эффект взаимодействия АВ. Порядок эффектов в векторе 'model' соответствует последовательности: А, В, АВ. Величина R(·) представляет остаточную сумму квадратов отклонений для модели, например R(A,B,AB) - остаточная сумма квадратов соответствующая полной модели, R(A) - остаточная сумма квадратов соответствующая главному эффекту фактора А, R(1) - остаточная сумма квадратов соответствующая общему среднему арифметическому. Три способа расчета суммы квадратов для рассматриваемого примера приведены в следующей таблице:
|
Эффект |
1 способ (sstype=1) |
2 способ (sstype=2) |
3 способ (sstype=3) |
|
A |
R(1)-R(A) |
R(B)-R(A,B) |
R(B,AB)-R(A,B,AB) |
|
B |
R(A)-R(A,B) |
R(A)-R(A,B) |
R(A,AB)-R(A,B,AB) |
|
AB |
R(A,B)-R(A,B,AB) |
R(A,B)-R(A,B,AB) |
R(A,B)-R(A,B,AB) |
Модели при расчете SS по третьему способу имеют ограничение по среднему квадратическому отклонению. Это означает, например для остаточной суммы квадратов R(B,AB), массив эффектов АВ ограничен по сумме от 0 до А для каждого значения В и до В для каждого значения А.
p = anovan(X,group,'model',sstype,gnames) входной аргумент gnames служит для определения меток N факторов в таблице дисперсионного анализа. gnames может быть задан как вектор строк или массив ячеек, содержащий строковые переменные, где каждый элемент массива соответствует одному наблюдению. Если входной аргумент gnames не задан, в качестве меток по умолчанию принимаются: 'X1', 'X2', 'X3',...,'XN'.
p = anovan(X,group,'model',sstype,gnames,'displayopt') входной аргумент 'displayopt' позволяет отобразить графическое окно с таблицей результатов дисперсионного анализа 'displayopt'='on', или подавить вывод графического окна 'displayopt'='off'. Значение по умолчанию 'displayopt'='on'.
[p,table] = anovan(...) функция возвращает таблицу с результатами многофакторного дисперсионного анализа, включая метки факторов, в текстовой форме в командное окно MATLAB.
[p,table,stats] = anovan(...) функция возвращает структуру stats используемую для проведения парных сравнений средних арифметических выборок. Проверка параметрической гипотезы о равенстве двух средних арифметических выполняется при помощи функции multcompare. Структура данных stats передается функции multcompare как входной аргумент.
[p,table,stats,terms] = anovan(...) функция возвращает вектор номеров главных эффектов и эффектов взаимодействий terms, использовавшихся при проведении многофакторного дисперсионного анализа. Формат задания оцениваемых эффектов terms соответствует формату вектора 'model'. Если при вызове anovan был использован вектор 'model', то terms='model'.
Примеры использования функции многофакторного дисперсионного анализа
Дисперсионный анализ для 3-х факторов изменяющихся двух уровнях.
>> X=normrnd(0,1,8,1)
X =
1.0668
0.0593
-0.0956
-0.8323
0.2944
-1.3362
0.7143
1.6236
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}}
group =
[1x8 double]
[8x2 char ]
{1x8 cell }
>> p = anovan(X,group)
p =
0.4968
0.7086
0.7562
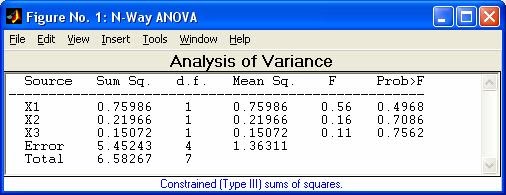
Дисперсионный анализ для 5-ти факторов изменяющихся 3-х уровнях.
>> X=normrnd(0,1,125,1)
>> group = unidrnd(3,125,3)
>> group = {group (1:125,1); group (1:125,2); group (1:125,3)}
>> p = anovan(X,group)
p =
0.5567
0.7518
0.2289
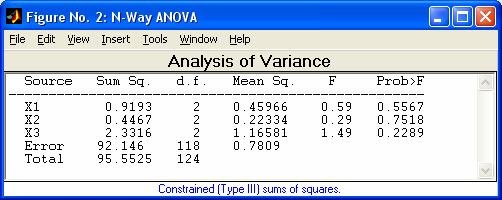
Дисперсионный анализ для 3-х факторов, изменяющихся двух уровнях, и модели, содержащей эффекты взаимодействий факторов.
>> X=normrnd(0,1,8,1);
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
>> model='interaction';
>> p = anovan(X,group,model)
p =
0.1140
0.1399
0.5655
0.3926
0.3103
0.1807
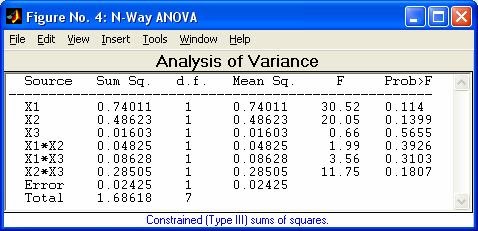
Дисперсионный анализ для 3-х факторов: А, В и С, изменяющихся двух уровнях, и model=[2 4 6] для проверки
нулевых гипотез относительно главных эффектов В и С и эффекта взаимодействия ВС.
>> X=normrnd(0,1,8,1);
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
>> model=[2 4 6];
>> p = anovan(X,group,model)
p =
0.7621
0.7667
0.4625
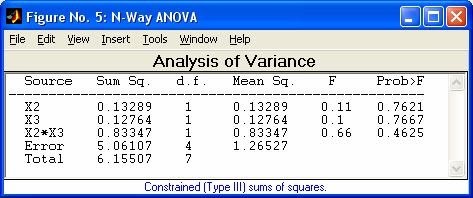
Дисперсионный анализ для 3-х факторов: А, В и С, изменяющихся двух уровнях, и model=[2 4 6] для проверки
нулевых гипотез относительно главных эффектов В и С и эффекта взаимодействия ВС. И второго способа расчета
суммы квадратов разностей (SS) по каждому виду дисперсии.
>> X=normrnd(0,1,8,1);
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
>> model=[2 4 6];
>> sstype = 2;
>> p = anovan(X,group,model, sstype)
p =
0.0810
0.4209
0.5171
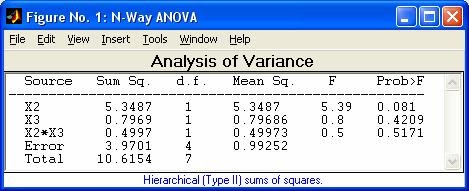
Дисперсионный анализ для 3-х факторов: А, В и С, изменяющихся двух уровнях, и model=[1 2 4 6] для проверки
нулевых гипотез относительно главных эффектов А, В, С и эффекта взаимодействия ВС. И второго способа расчета
суммы квадратов разностей (SS) по каждому виду дисперсии. В качестве меток используется массив ячеек
gnames = {'Xx'; 'Yy'; 'Zz'}.
>> X=normrnd(0,1,8,1);
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
>> model=[1 2 4 6];
>> sstype = 2;
>> gnames = {'Xx'; 'Yy'; 'Zz'};
>> p = anovan(X,group,model,sstype,gnames)
p =
0.4146
0.8676
0.4481
0.5157
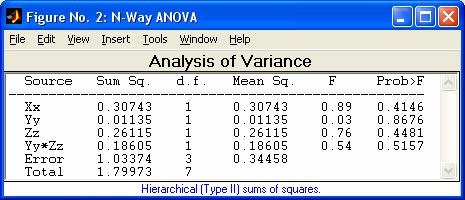
Дисперсионный анализ для 3-х факторов: А, В и С, изменяющихся двух уровнях, и модели, содержащей эффекты взаимодействий факторов. И второго способа расчета суммы квадратов разностей (SS) по каждому виду дисперсии. В качестве меток используется массив ячеек gnames = {'Xx'; 'Yy'; 'Zz'}. Кроме уровней значимости для указанных нулевых гипотез, выводятся таблица многофакторного дисперсионного анализа, структура для проведения парного сравнения средних, вектор использованных факторов и их взаимодействий.
>> X=normrnd(0,1,8,1);
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
>> model='interaction';
>> sstype = 2;
>> gnames = {'Xx'; 'Yy'; 'Zz'};
>> [p,table,stats,terms] = anovan(X,group,model,sstype,gnames)
p =
0.2308
0.2221
0.1346
0.0714
0.1167
0.3139
table =
'Source' 'Sum Sq.' 'd.f.' 'Singular?' 'Mean Sq.' 'F' 'Prob>F'
'Xx' [ 0.5218] [ 1] [ 0] [ 0.5218] [ 6.9526] [0.2308]
'Yy' [ 0.5675] [ 1] [ 0] [ 0.5675] [ 7.5609] [0.2221]
'Zz' [ 1.6290] [ 1] [ 0] [ 1.6290] [21.7042] [0.1346]
'Xx*Yy' [ 5.9145] [ 1] [ 0] [ 5.9145] [78.8050] [0.0714]
'Xx*Zz' [ 2.1852] [ 1] [ 0] [ 2.1852] [29.1156] [0.1167]
'Yy*Zz' [ 0.2599] [ 1] [ 0] [ 0.2599] [ 3.4627] [0.3139]
'Error' [ 0.0751] [ 1] [ 0] [ 0.0751] [] []
'Total' [11.1529] [ 7] [ 0] [] [] []
stats =
source: 'anovan'
coeffs: [7x1 double]
Rtr: [7x7 double]
dfe: 1
mse: 0.0751
permvec: [1 2 3 4 5 6 7]
terms: [6x1 double]
nlevels: [3x1 double]
termcols: [7x1 double]
terms =
1
2
4
3
5
6
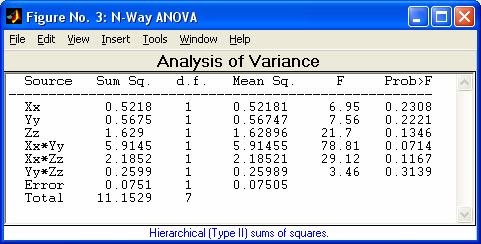
aoctool - Однофакторный анализ ковариационных моделей. Выходными параметрами функции являются:
Синтаксис
aoctool(x,y,g)
aoctool(x,y,g,alpha)
aoctool(x,y,g,alpha,xname,yname,gname)
aoctool(x,y,g,alpha,xname,yname,gname,'displayopt')
aoctool(x,y,g,alpha,xname,yname,gname,'displayopt','model')
h = aoctool(...)
[h,atab,ctab] = aoctool(...)
[h,atab,ctab,stats] = aoctool(...)
Описание
aoctool(x,y,g) функция позволяет провести парный ковариационный анализ для независимой переменной х и зависимой переменной y. g является группирующей переменной. Если g задает несколько отдельных групп пар значений x и y, то парный ковариационный анализ проводится для каждой подгруппы отдельно. Входные аргументы x, y, g задаются как векторы с одинаковой размерностью. В английской литературе этот вид анализа известен под аббревиатурой ANOCOVA.
Примечание: группирующая переменная g должна содержать значения делящие векторы x, y как минимум на две выборки, в противном случае будет выдано следующее сообщение об ошибке:
>> x=normrnd(100,1);
>> y=normrnd(100,1);
>> g=ones(100,1);
>> aoctool(x,y,g)
??? Error using ==> aoctool
Must have at least two groups
Результаты расчета функции aoctool представляются в 3-х графических окнах:
-
Окно интерактивного графика содержащего экспериментальные данные и линейное уравнение регрессии (рис. 1),
-
Окно с таблицей однофакторного дисперсионного анализа (рис. 2),
-
Окно с таблицей точечных и интервальных оценок параметров регрессионных моделей (рис. 3).
Элементы управления в графическом окне (рис. 1) позволяют изменять вид регрессионной модели и проводить в интерактивном режиме проверку гипотез об их соответствии экспериментальным данным. Результаты расчета и графики после изменения значений в элементах управления будут автоматически пересчитаны и отображены во всех 3-х графических окнах. Изменяя мышью положение пунктирной линии или соответствующее значение в строке ввода х (рис. 1) можно в интерактивном режиме рассчитать точечную и интервальную оценки зависимой переменной. Оценки зависимой переменной отображаются справа от графика. Этот расчет доступен, если в списке группировки g (рис. 1) выбрано любое значение кроме "All Groups".
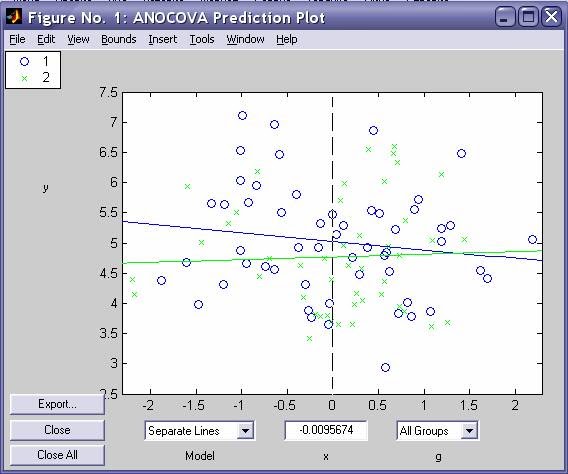
Рис. 1. Окно графика экспериментальных данных и линейной регрессионной модели
.jpg)
Рис. 2. Окно однофакторного дисперсионного анализа
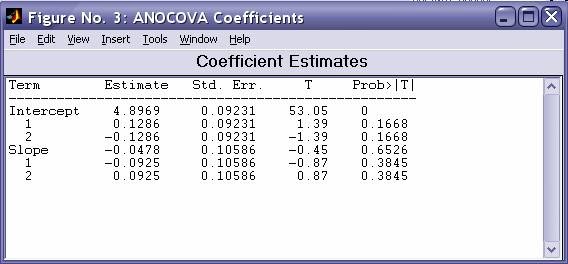
Рис. 3. Окно точечных и интервальных оценок параметров линейных регрессионных моделей
Список и функции элементов управления графического окна графика экспериментальных данных и линейной регрессионной модели приведены в таблице 1.
Таблица 1
|
Элемент управления |
Назначение |
|
|
Экспорт результатов расчета в среду MATLAB. Экспортируются следующие переменные (рис. 4): Parameters - параметры регрессионной модели; Parameter CI - доверительные интервалы параметров регрессионной модели; Prediction - значение зависимой переменной для текущего x; Prediction CI - границы доверительного интервала зависимой переменной; Residuals - вектор остатков. |
|
|
Закрытие окна графика экспериментальных данных и линейной регрессионной модели |
|
|
Закрытие всех окон |
|
|
Выбор типа модели из следующего списка (рис. 5):
Подробное описание регрессионных моделей см. в табл. 2. |
|
|
Интерактивное определение значение независимое переменной |
|
|
Выбор для проведения ANOCOVA одной группы, определяемой значением группирующей переменной g (рис. 6) и построение соответствующего графика c границами доверительного интервала. При выборе "All Groups" будут построены графики для всех подгрупп без границ доверительных интервалов. |
Рис. 4.
Рис. 5.
Рис. 6.
aoctool(x,y,g,alpha) входной аргумент alpha позволяет задать уровень значимости для расчета границ доверительного интервала. Доверительная вероятность определяется как 100*(1-alpha)%. По умолчанию уровень значимости принимается как 0,05.
aoctool(x,y,g,alpha,xname,yname,gname) входные аргументы xname, yname, gname позволяют задать названия входным аргументам x, y, g на графиках и в таблицах графических окон. Если в качестве входных аргументов x, y, g используются переменные aoctool использует их идентификаторы в качестве названий на выходных графиках и в таблицах. Входные аргументы xname, yname, gname необходимо использовать в случаях, когда для задания x,y,g используются выражения. Например, если в качестве х было использовано выделение 1 столбца матрицы m - m(:,1), то необходимо в качестве названия х использовать некоторую строковую константу xname='Col1'.
aoctool(x,y,g,alpha,xname,yname,gname,'displayopt') входной аргумент 'displayopt' позволяет явно задать отображение графических окон с результатами анализа 'displayopt'='on', или подавить вывод графических окон 'displayopt'='off'. Значение по умолчанию 'displayopt'='on'.
aoctool(x,y,g,alpha,xname,yname,gname,'displayopt','model') входной аргумент 'model' предназначен для задания начальной модели при проведении ковариационного анализа. Возможны следующие значения 'model':
-
'same mean' - определение общего среднего арифметического с игнорированием группировки значений x, y;
-
'separate means' - определение средних арифметических для каждой подгруппы;
-
'same line' - определение параметров линейной регрессионной модели с игнорированием группировки;
-
'parallel lines' - определение параметров линейных регрессионных моделей для каждой группы при условии, что линии уравнений регрессии должны быть параллельны друг другу;
-
'separate lines' - определение параметров линейных регрессионных моделей для каждой группы без каких либо ограничений.
Вид регрессионных моделей приведен в таблице 2.
Таблица 2.
|
Значение параметра 'model' |
Выражение |
|
Same mean |
|
|
Separate means |
|
|
Same line |
|
|
Parallel lines |
|
|
Separate lines |
|
Где ![]() - общее среднее по всем подгруппам (общее начальное смещение на графике);
- общее среднее по всем подгруппам (общее начальное смещение на графике); ![]() - погрешность математической модели;
- погрешность математической модели; ![]() - начальное смещение для i-й подгруппы экспериментальных значений относительно
- начальное смещение для i-й подгруппы экспериментальных значений относительно ![]() ;
; ![]() - коэффициент при первой степени независимой переменной для всех подгрупп (угол наклона линейной регрессионной модели к оси абсцисс);
- коэффициент при первой степени независимой переменной для всех подгрупп (угол наклона линейной регрессионной модели к оси абсцисс); ![]() - коэффициент при первой степени независимой переменной для i-й подгруппы экспериментальных значений относительно
- коэффициент при первой степени независимой переменной для i-й подгруппы экспериментальных значений относительно ![]() . Для регрессионных моделей отдельных групп с параллельными прямыми, 'model'="Parallel lines", величины углов наклона
. Для регрессионных моделей отдельных групп с параллельными прямыми, 'model'="Parallel lines", величины углов наклона ![]() примут одинаковые значения, значения начального смещения
примут одинаковые значения, значения начального смещения ![]() =var.
=var.
h = aoctool(...) функция возвращает вектор h указателей на линии графика.
[h,atab,ctab] = aoctool(...) кроме вектора указателей h, функция возвращает массив ячеек atab, содержащий результаты однофакторного дисперсионного анализа и отформатированную в текстовом виде таблицу значений точечных и интервальных оценок коэффициентов ctab.
[h,atab,ctab,stats] = aoctool(...) функция возвращает структуру stats, которая используется как входной аргумент функции multcompare, для выполнения процедуры парного сравнения параметров регрессионной модели. Таблица с результатами однофакторного дисперсионного анализа содержит сведения о результатах проверки нулевой гипотезы о равенстве всех начальных смещений (slopes) и коэффициентов при первой степени независимой переменной (intercepts) против альтернативной гипотезы, состоящей в том, что хотя бы одно из них значимо отличается от других. При проведении процедуры парного сравнения в качестве сравниваемых величин могут выступать: начальные смещения регрессионной модели, коэффициенты при линейных степенях регрессионной модели или общие средние (средние по подгруппам).
Примеры использования функции интерактивного графического ковариационного анализа
Рассматривается пример ковариационного анализа с целью определения наличия и вида взаимосвязи между массой автомобиля и величиной его пробега. Автотранспортные средства сгруппированы по годам выпуска: 1970, 1976, 1982.
Загрузка данных:
>> load carsmall
Переменные, содержащие выборочные данные приведены в окне Workspace Browser (рис. 7):
Рис. 7.
Acceleration - предельное ускорение автотранспортного средства,
Cylinders - количество цилиндров,
Displacement - расход топлива,
Horsepower - мощность,
MPG - пробег,
Model - название модели,
Model_Year - год выпуска,
Origin - страна-производитель,
Weight - масса автомобиля.
Проведение ковариационного анализа.
Рассматривается зависимость между массой автомобиля - Weight (независимая переменная) и пробегом - MPG (зависимая переменная) в зависимости от года выпуска - Model_Year (группирующая переменная). На выходе функция возвращает вектор h указателей на линии графика, результаты однофакторного дисперсионного анализа atab и таблицу значений точечных и интервальных оценок коэффициентов ctab регрессионной модели.
>> [h,atab,ctab,stats] = aoctool(Weight,MPG,Model_Year)
Note: 6 observations with missing values have been removed.
h =
101.0002
102.0002
103.0002
113.0002
114.0002
115.0002
116.0002
117.0002
atab =
Columns 1 through 5
'Source' 'd.f.' 'Sum Sq' 'Mean Sq' 'F'
'Model_Year' [ 2] [ 807.6896] [ 403.8448] [ 51.9762]
'Weight' [ 1] [2.0502e+003] [2.0502e+003] [263.8679]
'Model_Year*Weight' [ 2] [ 81.2188] [ 40.6094] [ 5.2266]
'Error' [ 88] [ 683.7420] [ 7.7698] []
Column 6
'Prob>F'
[1.2212e-015]
[ 0]
[ 0.0072]
[]
ctab =
'Term' 'Estimate' 'Std. Err.' 'T' 'Prob>|T|'
'Intercept' [ 45.9798] [ 1.5208] [ 30.2330] [2.9266e-048]
' 70' [ -8.5805] [ 1.9619] [ -4.3737] [3.3417e-005]
' 76' [ -3.8902] [ 1.8686] [ -2.0818] [ 0.0403]
' 82' [ 12.4707] [ 2.5568] [ 4.8775] [4.7391e-006]
'Slope' [ -0.0078] [5.5717e-004] [-14.0031] [4.0955e-024]
' 70' [ 0.0020] [6.6152e-004] [ 2.9605] [ 0.0039]
' 76' [ 0.0011] [6.5328e-004] [ 1.7425] [ 0.0849]
' 82' [ -0.0031] [9.9914e-004] [ -3.0994] [ 0.0026]
stats =
source: 'aoctool'
gnames: {3x1 cell}
n: [3x1 double]
df: 88
s: 2.7874
model: 5
slopes: [3x1 double]
slopecov: [3x3 double]
intercepts: [3x1 double]
intercov: [3x3 double]
pmm: [3x1 double]
pmmcov: [3x3 double]
Анализ результатов расчета.
На рис. 8 представлено графическое окно, показывающее зависимость пробега автомобиля от его массы. Автотранспортные средства разделены на 3 группы по годам выпуска: 1970, 1976, 1982. На графике группы обозначены как 70, 76, 82 соответственно. Экспериментальные точки и соответствующие им регрессионные модели выделены одинаковым цветом.
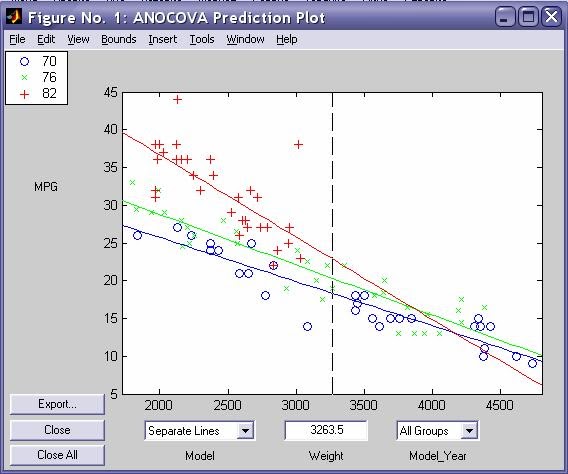
Рис. 8. Окно графиков экспериментальных данных и линейных регрессионных моделей
Значения коэффициентов регрессионных моделей приведены в графическом окне ANOCOVA Coefficients (рис. 9) - окне, содержащем точечные и интервальные оценок параметров линейных регрессионных моделей, а также статистики Стьюдента T и уровня значимости Prob предназначенных для проверки нулевой гипотезы о значимости полученных значений.
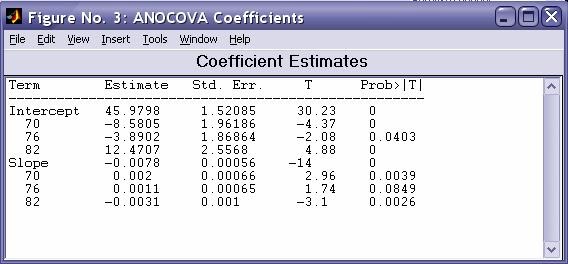
Рис. 9. Окно точечных и интервальных оценок параметров линейных регрессионных моделей
Из полученных результатов следует, что коэффициент при первой степени независимой переменной мало зависит от года выпуска и составляет приблизительно -0, 0078 с незначительными отклонениями:
|
Год выпуска 1970 |
|
|
Год выпуска 1976 |
|
|
Год выпуска 1982 |
|
Полученный результат на графике экспериментальных значений (рис. 8) соответствует приблизительно одинаковому углу наклона прямых регрессионных моделей.
Эффект взаимодействия Model_Year*Weight позволяет оценить значимость различия в коэффициентах при линейной степени независимой переменной (углах наклона регрессионных моделей на рис. 8). Результаты оценки значимости эффекта взаимодействия и главных эффектов приведены в таблице результатов однофакторного дисперсионного анализа (ANOVA table рис. 10).
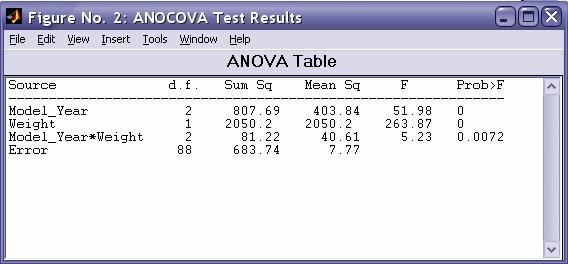
Рис. 10. Окно однофакторного дисперсионного анализа
Значения статистики Фишера F= 5.23 и уровне значимости p=0,0072 позволяет сделать вывод о значимом различии в линейных коэффициентах при первой степени независимой переменной.
Для оценки степени соответствия линейных регрессионных моделей с ограничениями на равенство коэффициентов при первых степенях независимых переменных 'model'='parallel lines' и предыдущего случая 'model'='separate lines' необходимо в графическом окне экспериментальных данных (рис. 8) изменить значение в списке Model на соответствующее значение (рис. 11).
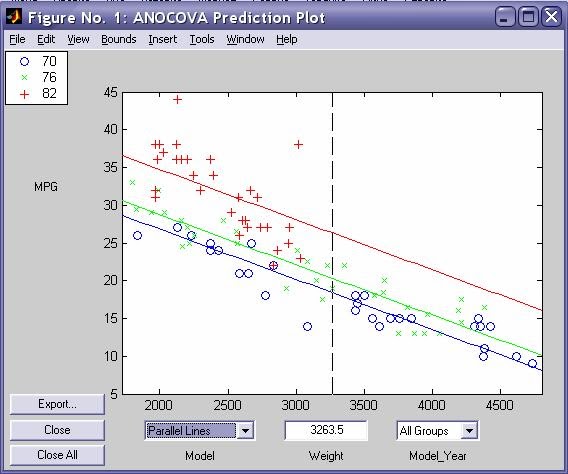
Рис. 11. Окно графиков экспериментальных данных и линейных регрессионных моделей для 'model'='parallel lines'
После изменения вида регрессионных моделей будут построены новые зависимости и пересчитаны все статистики в графических окнах (рис. 12, 13).
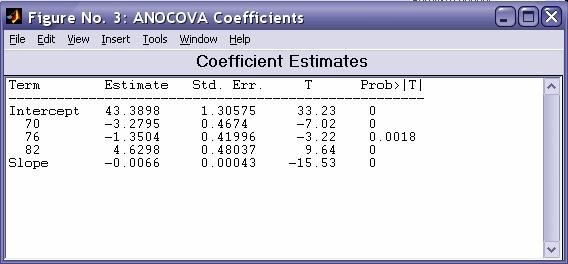
Рис. 12. Окно точечных и интервальных оценок параметров линейных регрессионных моделей для 'model'='parallel lines'
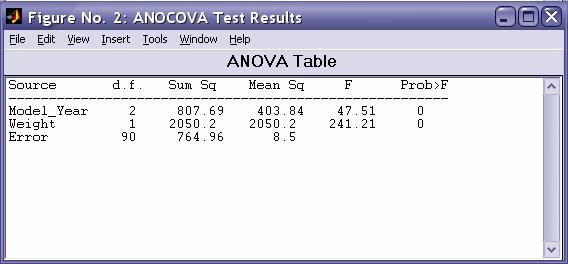
Рис. 13. Окно однофакторного дисперсионного анализа для 'model'='parallel lines'
Полученные результаты свидетельствуют о том, что линейные модели без ограничений на значения линейных коэффициентов предпочтительнее.
Для исследования зависимости между пробегом массой автотранспортных средств в отдельной группе и погрешности полученных моделей используется список Model_Year. В предположении линейной зависимости между переменными границы доверительного интервала будут соответствовать 95% доверительной вероятности. Для моделей выпуска 1982 года зависимость между зависимой и независимой переменными с учетом границ доверительного интервала примет вид (рис. 14, Model_Year=82):
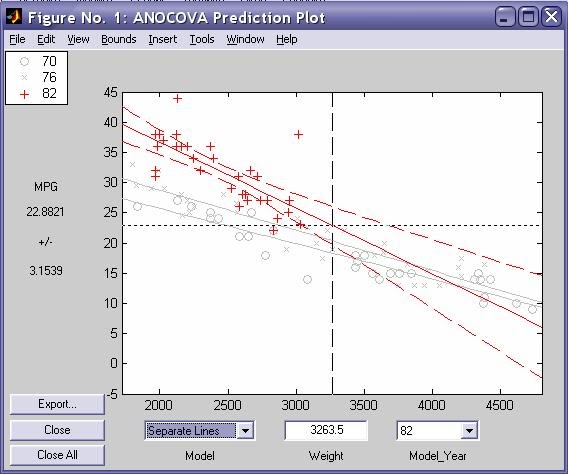
Рис. 14. Окно графиков экспериментальных данных, линейной регрессионной модели и границ ее доверительных интервалов для 'model'='separate lines' и Model_Year=82
В некоторых случаях целесообразно рассчитывать границы доверительного интервала для отдельного или нового наблюдения, а не среднего значения зависимой переменной. Переключение способа расчета границ доверительного интервала для отдельного наблюдения используется команда меню Bounds/Observation. Команда Bounds/Line позволяет вернуться для расчета границ доверительного интервала по среднему значению. Переключение между способами расчета границ доверительного интервала имеет смысл для отдельных групп. Поэтому сначала необходимо в списке Model выбрать интересующее значений группирующей переменной. Для Model_Year=82 границы доверительного интервала для отдельных значений пример вид (рис. 15)
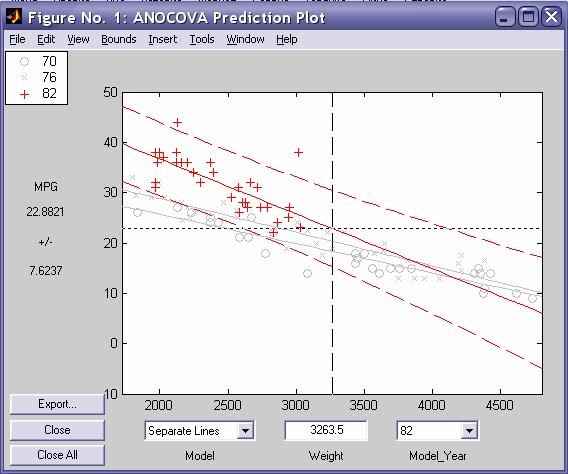
Рис. 15. Окно графиков экспериментальных данных, линейной регрессионной модели и границ ее доверительных интервалов для 'model'='separate lines' и Model_Year=82 по отношению к отдельным наблюдениям
По аналогии с интерактивным интерфейсом функции polytool, мышью (или введя новое значение в строку Weight) можно изменить положение пунктирной линии по оси абсцисс, и получить новое значений зависимой переменной MPG по регрессионной модели и границы ее доверительного интервала. Этот способ определения точечной и интервальной оценок используется только для выбранной определенной подгруппы в списке группирующей переменной Model_Year. Если в списке значений группирующей переменной Model_Year выбрано значение "All Groups", этот способ определения точечной и интервальной оценок не предусмотрен.
Процедура парного сравнения параметров регрессионных моделей или маргинальных средних.
Для проведения процедуры парного сравнения используется функция multcompare. Входным аргументом multcompare является структура stats, полученная в результате вызова функции aoctool. Процедура парного сравнения может быть применена для параметров линейных регрессионных моделей, полученных для различных значений группирующей переменной, или маргинальных средних. Маргинальными средними для рассматриваемого примера являются рассчитанные по регрессионной модели значения зависимой переменной MPG для среднего веса каждой подгруппы.
Выполняется парное сравнение коэффициентов при первой степени независимой переменой. Как было показано в предыдущих пунктах ковариационного анализа, угол наклона линейных регрессионных моделей должен быть различным. Применение процедуры парного сравнения позволяет определить пару коэффициентов статистически значимо отличающихся друг от друга.
Вызов функции парного сравнения:
>> multcompare(stats,0.05,'on','','s')
ans =
1.0000 2.0000 -0.0012 0.0008 0.0029
1.0000 3.0000 0.0013 0.0051 0.0088
2.0000 3.0000 0.0005 0.0042 0.0079
Из первой строки матрицы ans следует, что разница между коэффициентами при первой степени независимой переменой первой и второго подгрупп экспериментальных значений (модели выпуска 1970 и 1976 годов) составила 0.0008 с границами доверительного интервала [-0.0012, 0.0029]. Так как доверительный интервал включает нулевой значение, то разница между коэффициентами статистически не значима. Из 2-х последующих строк матрицы ans можно сделать вывод о значимом отличии между соответствующими коэффициентами 2 и 3, 1 и 3 подгрупп, так как нулевое значение не попадает в границы доверительных интервалов разностей указанных значений. График разностей значений коэффициентов при первой степени независимой переменой для 1, 2, 3 групп и их доверительных интервалов представлен на рис. 16.
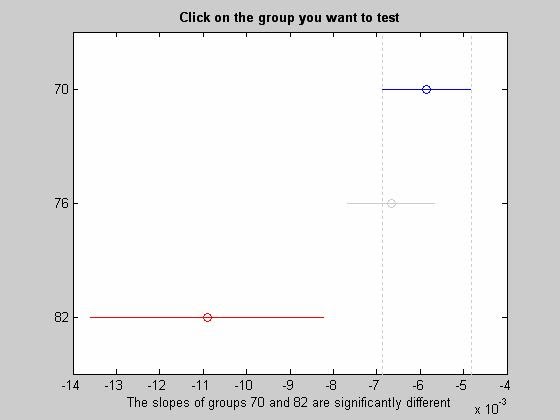
Рис. 16. Графическое окно результатов парного сравнения разностей значений коэффициентов при первой степени независимой переменой для групп "70", "76", "82" и их доверительных интервалов
Следует заметить, что структура stats была получена для значения "model" по умолчанию и не может быть изменена в интерактивном режиме. Проведение парного сравнения для других моделей потребует явно задать входной аргумент "model" функции aoctool, и затем полученную структуру stats передать как входной аргумент multcompare.
dummyvar - Условное кодирование переменных.
Синтаксис
D = dummyvar(group)
Описание
D = dummyvar(group) функция позволяет получить матрицу фиктивных переменных D, содержащую единицы и нули. Единичные значения в D соответствуют наличию определенного элемента в матрице group, нулевые - отсутствие соответствующего элемента. Элементами матрицы group должны быть положительные целые числа. Количество строк матриц group и D будет одинаковым. Количество столбцов в матрице D будет определяться суммой чисел возможных значений в столбцах матрицы group.
Матрица D формируется следующим образом:
-
Формируется пустая матрица D с числом строк равным количеству строк в исходной матрице group и количеством столбцов равным сумме чисел возможных значений в столбцах матрицы group. Например, если матрица group задана как
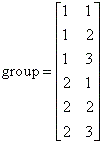
то матрица фиктивных переменных D примет следующий вид
Количество столбцов матрицы D будет равно 2+3, где 2 - число возможных значений в первом столбце: 1, 2; 3 - число возможных значений во втором столбце: 1, 2, 3.
-
Элементы матрицы D заполняются "1". Столбцы матрицы D соответствуют возможным значениям первого столбца, затем второго и т.д. Для рассмотренного выше примера
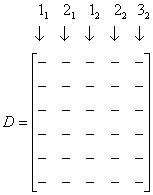
где 11 , 21 - значения 1, 2 из первого столбца group, 12 , 22 , 32 - значения 1, 2, 3 из второго столбца group.
Далее выполняется построчное заполнение "1" элементов матрицы D согласно строкам group. "1" ставятся в позициях соответствующих значениям элементов group. Например, в первой строке приведенной выше матрице group указаны единичные значения первого и второго столбца [1 1] , тогда подставляя "1" на соответствующие предыдущей схеме места получим первую строку D - [1 - 1 - - -] . В итоге сформируется следующая матрица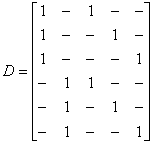
-
Пустые позиции заполняются "0". Для рассматриваемого примера получим
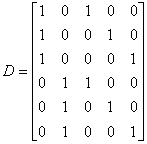
Примеры использования функции формирования матрицы фиктивных переменных
Рассмотрим формирование матрицы фиктивных переменных согласно приведенному в описании функции dummyvar.
>> group = [1 1;1 2;1 3;2 1;2 2;2 3]
group =
1 1
1 2
1 3
2 1
2 2
2 3
>> D = dummyvar(group)
D =
1 0 1 0 0
1 0 0 1 0
1 0 0 0 1
0 1 1 0 0
0 1 0 1 0
0 1 0 0 1
Поскольку матрица фиктивных переменных часто используется в планировании эксперимента рассмотрим следующий пример.
Изучаются эффекты от работы 3 операторов на 3 станках.
В этом случае матрица group будет соответствовать сочетаниям уровней переменных
>> group = [1 1 1; 1 1 2; 1 1 3; 1 2 1; 1 2 2; 1 2 3; 1 3 1; 1 3 2; 1 3 3; 2 1 1; 2 1 2; 2 1 3;
2 2 1; 2 2 2; 2 2 3; 2 3 1; 2 3 2; 2 3 3; 3 1 1; 3 1 2; 3 1 3; 3 2 1; 3 2 2; 3 2 3; 3 3 1; 3 3 2; 3 3 3;]
group =
1 1 1
1 1 2
1 1 3
1 2 1
1 2 2
1 2 3
1 3 1
1 3 2
1 3 3
2 1 1
2 1 2
2 1 3
2 2 1
2 2 2
2 2 3
2 3 1
2 3 2
2 3 3
3 1 1
3 1 2
3 1 3
3 2 1
3 2 2
3 2 3
3 3 1
3 3 2
3 3 3
>> D = dummyvar(group)
D =
1 0 0 1 0 0 1 0 0
1 0 0 1 0 0 0 1 0
1 0 0 1 0 0 0 0 1
1 0 0 0 1 0 1 0 0
1 0 0 0 1 0 0 1 0
1 0 0 0 1 0 0 0 1
1 0 0 0 0 1 1 0 0
1 0 0 0 0 1 0 1 0
1 0 0 0 0 1 0 0 1
0 1 0 1 0 0 1 0 0
0 1 0 1 0 0 0 1 0
0 1 0 1 0 0 0 0 1
0 1 0 0 1 0 1 0 0
0 1 0 0 1 0 0 1 0
0 1 0 0 1 0 0 0 1
0 1 0 0 0 1 1 0 0
0 1 0 0 0 1 0 1 0
0 1 0 0 0 1 0 0 1
0 0 1 1 0 0 1 0 0
0 0 1 1 0 0 0 1 0
0 0 1 1 0 0 0 0 1
0 0 1 0 1 0 1 0 0
0 0 1 0 1 0 0 1 0
0 0 1 0 1 0 0 0 1
0 0 1 0 0 1 1 0 0
0 0 1 0 0 1 0 1 0
0 0 1 0 0 1 0 0 1
glmfit - Определение параметров обобщенной линейной модели
Синтаксис
b = glmfit(X,Y,'distr')
b = glmfit(X,Y,'distr','link','estdisp',offset,pwts,'const')
[b,dev,stats] = glmfit(...)
Описание
b = glmfit(X,Y,'distr') функция предназначена для оценки параметров обобщенной линейной регрессионной модели. Входными аргументами функции являются: Y - зависимая переменная, X - матрица независимых переменных, 'distr' - строковая переменная, определяющая вид распределения зависимой переменной.
Предусмотрены следующие распределения зависимой переменной
|
Значение 'distr' |
Вид распределения |
|
'binomial' |
Биномиальное |
|
'gamma' |
Гамма |
|
'inverse gaussian' |
Обратное распределение Гаусса |
|
'lognormal' |
Логнормальное |
|
'normal' |
Нормальное (значение 'distr' по умолчанию) |
|
'poisson' |
Пуассона |
Для всех распределений, кроме биномиального, зависимая переменная Y задается как вектор. Для биномиального закона Y должна быть определена как матрица с двумя столбцами: в первом столбце задается число благоприятных событий, во втором - число повторных независимых испытаний. Матрица независимых переменных Х должна содержать такое же количество строк, что и Y.
Примечание автора: несмотря на отмеченную возможность использовать distr='lognormal' функция glmfit в версиях Statistics Toolbox 4, 4.1 не содержит соответствующего кода.
Выходная переменная b - вектор точечных оценок коэффициентов линейной обобщенной регрессионной модели. Этот вариант синтаксиса вызова функции glmfit использует каноническую взаимосвязь (см. ниже) параметров распределения с независимыми переменными.
b = glmfit(X,Y,'distr','link','estdisp',offset,pwts,'const') входные аргументы 'link', 'estdisp', offset, pwts, 'const' предназначены для управления процессом оценки параметров регрессионной модели. Входной аргумент 'link' задает вид взаимосвязи между параметром распределения ![]() и оцениваемой линейной комбинацией независимых переменных
и оцениваемой линейной комбинацией независимых переменных ![]() . Предусмотрены следующие значения 'link'
. Предусмотрены следующие значения 'link'
|
Значение 'link' |
Вид зависимости |
Взаимосвязь по умолчанию (каноническая) |
|
'identity' |
µ = xb |
'normal' |
|
'log' |
log(µ) = xb |
'poisson' |
|
'logit' |
log(µ/ (1-µ)) = xb |
'binomial' |
|
'probit' |
norminv(µ) = xb |
|
|
'comploglog' |
log(-log(1-µ)) = xb |
|
|
'logloglink' |
log(-log(µ)) = xb |
|
|
'reciprocal' |
1/µ = xb |
'gamma' |
|
p (число) |
µp = xb |
'inverse gaussian' (если p=-2) |
Реализация другого вида взаимосвязи осуществляется при помощи inline или m функций. Аргумент 'link', определяющий вид произвольной взаимосвязи, задается как массив ячеек, содержащий 3 элемента: 1-й элемент содержит определение функции взаимосвязи; 2-й элемент - производную от функции взаимосвязи; 3-й элемент - ее обратную функцию. Ниже приведен пример формирования массива ячеек mylinks функций взаимосвязи на основе inline-функций:
FL = inline('x.^-.5')
FD = inline('-.5*x.^-1.5')
FI = inline('x.^-2')
mylinks = {FL FI FD}.
При использовании m-функций массив ячеек формируется по следующему правилу:
mylinks = {@FL @FD @FI}.
Входной аргумент 'estdisp' позволяет задать величину дисперсии выборки для биномиального закона и распределения Пуассона. Если 'estdisp'='on', то величина дисперсии оценивается по выборочным данным X, Y. Для 'estdisp'='off' точечная оценка дисперсии принимается равной 1. Для других распределений в glmfit значение дисперсии рассчитывается во всех случаях.
Аргумент offset является специальной независимой переменной с коэффициентом в регрессионной модели равным единице. В качестве примера использования offset можно рассмотреть моделирование числа дефектов на различных поверхностях. Требуется получить регрессионную модель, у которой зависимой переменной является относительное количество дефектов на единицу площади поверхности. В этом случае количество дефектов будет использоваться как зависимая переменная, распределенная по закону Пуассона, логарифмическая функция (log) будет использована для задания вида взаимосвязи между параметром распределения и оцениваемой линейной комбинацией независимых переменных (параметр 'link') и в качестве параметра offset будет выступать вектор логарифма от площади поверхности.
Аргумент pwts позволяет задать вектор весовых значений зависимой переменной. Например, если значение зависимой переменной Y(i) является средним арифметическим от f(i) измерений, то f может быть использован как вектор весовых значений.
Входные параметры offset и pwts могут быть заданы как векторы или пропущены при вызове функции. Пустые векторы offset и pwts будут трактоваться как пропущенные входные параметры. Размерность Y, offset и pwts должна совпадать.
Входной параметр 'const' позволяет в явном виде определить будет ли рассчитываться оценка постоянного члена регрессионной модели 'const'='on' или нет - 'const'='off'. Значение по умолчанию 'const'='on'. Если необходимо получить оценку постоянного члена регрессионной модели, то рекомендуется использовать 'const'='on' вместо задания единичного столбца в матрице независимых переменных.
[b,dev,stats] = glmfit(...) функция возвращает отклонения в векторе решений dev и структуру stats. Отклонения в векторе решений являются обобщением остаточной суммы квадратов и используются для сравнения ряда регрессионных моделей, состав коэффициентов одной из которых является подмножеством коэффициентов другой. В результате проводимого сравнения должно быть сделано статистически значимое заключение, что погрешность описания экспериментальных данных регрессионной моделью с большим количеством коэффициентов меньше, чем у модели с меньшим числом коэффициентов. Т.е., выбирается регрессионная модель с меньшим числом коэффициентов, обеспечивающая минимальную погрешность. Структура stats содержит следующую информацию:
-
stats.dfe - число степеней свободы погрешности регрессионной модели;
-
stats.s - теоретическая или оцененная дисперсия параметра;
-
stats.sfit - оценка дисперсии параметра;
-
stats.estdisp - 1 - если оценка дисперсии была рассчитана, 0 - если оценка дисперсии была задана;
-
stats.beta - вектор коэффициентов линейной обобщенной регрессионной модели (равен выходному параметру b);
-
stats.se - вектор стандартных ошибок коэффициентов линейной обобщенной регрессионной модели b;
-
stats.coeffcorr - матрица коэффициентов корреляции коэффициентов b;
-
stats.t - значение статистики t Стьюдента для вектора коэффициентов b;
-
stats.p - значение уровня значимости p статистики t Стьюдента для вектора коэффициентов b;
-
stats.resid - вектор остатков;
-
stats.residp - вектор остатков Пирсона;
-
stats.residd - вектор остатков обобщенной остаточной суммы квадратов;
-
stats.resida - вектор остатков Анскомбе.
Если рассчитывается оценка дисперсии параметра для биномиального закона или распределения Пуассона, то stats.s=stats.sfit. Элементы вектора stats.se будут отличаться от их теоретических значений на величину stats.s.
Примеры использования функции обобщенной линейной регрессии
Расчет параметров обобщенной линейной регрессионной модели для 5 независимых переменных распределенных по нормальному закону и зависимой переменной распределенной по нормальному закону. Вид распределения зависимой переменной задан как нормальный.
>> x=normrnd(0,1,100,5);
>> y =normrnd(0,1,100,1);
>> distr='normal'
distr =
normal
>> b = glmfit(x,y,distr)
b =
-0.0796
0.0073
-0.0456
0.1781
-0.1033
-0.1262
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых и зависимой переменным распределенным по Гамма закону. Вид распределения зависимой переменной задан как Гамма. Вид взаимосвязи между параметром распределения ![]() и оцениваемой линейной комбинацией независимых переменных
и оцениваемой линейной комбинацией независимых переменных ![]() задан как логарифмический.
задан как логарифмический.
>> x=gamrnd(1,2,100,3);
>> y = gamrnd(1,2,100,1);
>> distr='gamma';
>> link='log';
>> b = glmfit(x,y,distr, link)
b =
0.5814
0.0004
-0.0318
0.0021
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых и зависимой переменным, распределенным по нормальному закону. Вид распределения зависимой переменной задан как нормальный. Зависимость между параметром распределения и оцениваемой линейной комбинацией независимых переменных задана как ![]() в виде inline функций.
в виде inline функций.
>> x= normrnd (0,1,100,3);
>> y = normrnd (0,1,100,1);
>> distr='normal';
>> FL = inline('x.^.5')
FL =
Inline function:
FL(x) = x.^.5
>> FD = inline('.5*x.^-0.5')
FD =
Inline function:
FD(x) = .5*x.^-0.5
>> FI = inline('x.^2')
FI =
Inline function:
FI(x) = x.^2
>> link = {FL FI FD}
link =
[1x1 inline] [1x1 inline] [1x1 inline]
>> b = glmfit(x,y,distr, link)
Warning: Iteration limit reached.
> In F:\MATLAB6p5p1\toolbox\stats\glmfit.m at line 142
b =
1.1230 + 4.2739i
0.0081 - 0.2360i
0.0646 - 0.4430i
0.1076 - 0.8553i
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых и зависимой переменных, распределенным по нормальному закону. Вид распределения зависимой переменной задан как нормальный. Зависимость между параметром распределения и оцениваемой линейной комбинацией независимых переменных задана как ![]() в виде m-функций.
в виде m-функций.
m-файл функции взаимосвязи
function y= FL(X)
y=2.*X.^2;
m-файл производной функции взаимосвязи
function y= FD(X)
y=4.*X;
m-файл обратной функции взаимосвязи
function y= FI(X)
y=sqrt(1/2.*X);
Решение задачи обобщенной линейной регрессии в командном окне matlab
>> x= normrnd (0,1,100,3);
>> y = normrnd (0,1,100,1);
>> distr='normal';
>> link = {@FL @FD @FI}
link =
[@FL] [@FD] [@FI]
>> b = glmfit(x,y,distr, link)
Warning: Iteration limit reached.
> In F:\MATLAB6p5p1\toolbox\stats\glmfit.m at line 142
b =
-0.4225 -49.7205i
1.6578 +54.3794i
0.2324 +14.5554i
-0.4714 - 9.5040i
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых переменных распределенных по нормальному закону и зависимой переменной распределенной по закону Пуассона. Вид распределения зависимой переменной задан как закон Пуассона. Вид взаимосвязи между параметром распределения и оцениваемой линейной комбинацией независимых переменных задан как логарифмический. В явном виде выполняется расчет оценки дисперсии выборки.
>> x=normrnd(0,1,100,3);
>> y = poissrnd(0.5,100,1);
>> distr='poisson';
>> link='log';
>> estdisp='on';
>> b = glmfit(x,y,distr, link, estdisp)
b =
-0.7063
0.1773
-0.1130
-0.2340
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых переменных распределенных по нормальному закону и зависимой переменной распределенной по закону Пуассона. Вид распределения зависимой переменной задан как закон Пуассона. Вид взаимосвязи между параметром распределения и оцениваемой линейной комбинацией независимых переменных задан как логарифмический. В качестве дисперсии выборки принимается единица. Задана специальная независимая переменная offset как натуральный логарифм от зависимой переменной.
>> x=normrnd(0,1,100,3);
>> y = poissrnd(5,100,1);
>> distr='poisson';
>> link='log';
>> estdisp='off';
>> offset = log(y);
>> b = glmfit(x,y,distr, link, estdisp, offset)
b =
1.0e-015 *
0.1008
0.0001
0.0157
-0.0035
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых переменных. Вид распределения зависимой переменной задан как нормальный закон. Вид взаимосвязи между параметром распределения и оцениваемой линейной комбинацией независимых переменных задан как логарифмический. В качестве дополнительного параметра задан вектор весовых коэффициентов pwts.
>> x=1:1:10;
>> x=[x' x' x'];
>> xs= normrnd(0,1,10,3);
>> x=x+xs;
>> y =1:1:10;
>> ys= normrnd(0,1,10,1);
>> y=y+ys';
>> distr='normal';
>> link='identity';
>> estdisp=[];
>> offset = [];
>> pwts=unidrnd(10,10,1);
>> b = glmfit(x,y,distr, link, estdisp, offset, pwts)
b =
0.0062
-0.0272
0.7454
0.3303
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых переменных. Вид распределения зависимой переменной задан как нормальный закон. Вид взаимосвязи между параметром распределения и оцениваемой линейной комбинацией независимых переменных задан как логарифмический. В качестве дополнительного параметра задан вектор весовых коэффициентов pwts. Расчет выполняется без учета постоянного члена регрессионной модели.
>> x=1:1:10;
>> x=[x' x' x'];
>> xs= normrnd(0,1,10,3);
>> x=x+xs;
>> y =1:1:10;
>> ys= normrnd(0,1,10,1);
>> y=y+ys';
>> distr='normal';
>> link='identity';
>> estdisp=[];
>> offset = [];
>> pwts=unidrnd(10,10,1);
>> const='off';
>> b = glmfit(x,y,distr, link, estdisp, offset, pwts, const)
b =
-0.0282
0.7478
0.3297
Расчет параметров обобщенной линейной регрессионной модели для 3 независимых переменных. Вид распределения зависимой переменной задан как нормальный. Функция glmfit возвращает вектор коэффициентов регрессионной модели, отклонения в векторе решений dev и структуру stats.
>> x=normrnd(0,1,10,3);
>> y =normrnd(0,1,10,1);
>> distr='normal'
>> [b,dev,stats] = glmfit(x,y,distr)
b =
-0.2641
-0.0104
0.2923
0.2356
dev =
2.1690
stats =
beta: [4x1 double]
dfe: 6
sfit: 0.6012
estdisp: 1
s: 0.6012
se: [4x1 double]
coeffcorr: [4x4 double]
t: [4x1 double]
p: [4x1 double]
resid: [10x1 double]
residp: [10x1 double]
residd: [10x1 double]
resida: [10x1 double]
Значение полей структуры stats:
>> stats.beta
ans =
-0.2641
-0.0104
0.2923
0.2356
>> stats.se
ans =
0.2121
0.2274
0.1442
0.2936
>> stats.coeffcorr
ans =
1.0000 0.2628 0.1062 -0.2891
0.2628 1.0000 0.1491 0.2243
0.1062 0.1491 1.0000 -0.1506
-0.2891 0.2243 -0.1506 1.0000
>> stats.t
ans =
-1.2448
-0.0459
2.0264
0.8024
>> stats.p
ans =
0.2596
0.9649
0.0891
0.4529
>> stats.resid
ans =
0.2618
-0.6770
0.7166
-0.1264
-0.2909
0.3721
0.3868
-0.0347
0.2220
-0.8304
>> stats.residp
ans =
0.2618
-0.6770
0.7166
-0.1264
-0.2909
0.3721
0.3868
-0.0347
0.2220
-0.8304
>> stats.residd
ans =
0.2618
-0.6770
0.7166
-0.1264
-0.2909
0.3721
0.3868
-0.0347
0.2220
-0.8304
>> stats.resida
ans =
0.2618
-0.6770
0.7166
-0.1264
-0.2909
0.3721
0.3868
-0.0347
0.2220
-0.8304
Рассмотрим пример обобщенной линейной регрессии для числа автомобилей удовлетворяющих требованиям по расходу топлива на 1 милю в зависимости от их веса. Выборка экспериментальных значений задана следующими случайными величинами: w - масса автомобиля в фунтах, poor - количество автомобилей соответствующих спецификации из числа использованных при проведении испытаний для каждого значения w, total - общее число автотранспортных средств для каждой величины массы использованных при испытаниях.
>> w = (2100:200:4300)'
w =
2100
2300
2500
2700
2900
3100
3300
3500
3700
3900
4100
4300
>> poor = [1 2 0 3 8 8 14 17 19 15 17 21]';
>> total = [48 42 31 34 31 21 23 23 21 16 17 21]';
Поскольку в задаче рассматривается число удачных исходов при повторных независимых испытаниях, то в качестве закона распределения целесообразно принять биномиальное распределение. В качестве регрессионных моделей на начальном этапе обобщенного линейного регрессионного анализа принимаются зависимости: logit и probit.
>> [bl,dl,sl] = glmfit(w,[poor total],'binomial');
>> [bp,dp,sp] = glmfit(w,[poor total],'binomial','probit');
>> dl
dl =
6.4842
>> dp
dp =
7.5693
Значение отклонения в векторе решений модели logit меньше чем тоже отклонение для зависимости probit, т.е. dl<dp. Несмотря на то, что это отношение не является формальным общепринятым тестом, этот результат дает основание рассматривать модель logit как более предпочтительную по отношению к probit.
Рассмотрим две logit модели. В первой модели, рассмотренной выше, используется линейный эффект от независимой переменной w. В качестве второй примем модель с квадратичным и линейным эффектами w. Для сравнения регрессионных зависимостей будет использован тест на основе статистики ![]() . Нулевая гипотеза состоит в том, что если эффект от квадратичного эффекта w статистически не значим, то уровень значимости будет меньше критического значения равного 0,05. Значения уровня значимости рассчитывается для правосторонней критической области распределения
. Нулевая гипотеза состоит в том, что если эффект от квадратичного эффекта w статистически не значим, то уровень значимости будет меньше критического значения равного 0,05. Значения уровня значимости рассчитывается для правосторонней критической области распределения ![]() . В качестве параметров закона
. В качестве параметров закона ![]() при расчете уровня значимости выступают разница отклонений в векторах решений для рассматриваемых моделей и степень свободы, равная 1.
при расчете уровня значимости выступают разница отклонений в векторах решений для рассматриваемых моделей и степень свободы, равная 1.
Расчет отклонения в векторе решений для второй logit модели:
>> [b2,d2,s2] = glmfit([w w.^2],[poor total],'binomial');
>> d2
d2 =
5.7815
Величина разницы отклонений в векторах решений для рассматриваемых моделей:
>> dl-d2
>> ans =
0.7027
Расчет уровня значимости для разницы отклонений в векторах решений для рассматриваемых моделей
>> chi2cdf(dl-d2,1)
ans =
0.5981
Поскольку полученное значений уровня значимости 0.5981 больше критического 0.05, то оснований отвергнуть нулевую гипотезу нет, т.е. квадратический эффект массы автотранспортного средства ![]() статистически не значим по сравнению с линейным. Соответственно, нет оснований считать полную регрессионную модель с учетом квадратического и линейного эффектов массы автотранспортных средств предпочтительней, чем линейную модель.
статистически не значим по сравнению с линейным. Соответственно, нет оснований считать полную регрессионную модель с учетом квадратического и линейного эффектов массы автотранспортных средств предпочтительней, чем линейную модель.
Ниже приведены значения коэффициентов (b) линейной модели, стандартных ошибок (sl.se), t статистик (sl.t), уровней значимости (sl.p) для этих коэффициентов.
>> [bl sl.se sl.t sl.p]
ans =
-13.3801 1.3940 -9.5986 0.0000
0.0042 0.0004 9.4474 0.0000
Полученные результаты позволяют сделать вывод о невозможности далее упрощать полученную линейную модель. Оба коэффициента: постоянный член и коэффициент при линейной степени, значимо отличаются от нуля поскольку в обоих случаях величина уровня значимости равна 0.0000 до 4 значимых разрядов после запятой.
glmval - Прогнозирование с использованием обобщенной линейной модели
Синтаксис
yfit = glmval(b,X,'link')
[yfit,dlo,dhi] = glmval(b,X,'link',stats,clev)
[yfit,dlo,dhi] = glmval(b,X,'link',stats,clev,N,offset,'const')
Описание
yfit = glmval(b,X,'link') функция предназначена для расчета зависимой переменной yfit для значений независимой переменной Х на основе вектора коэффициентов линейной обобщенной регрессионной модели b и функции взаимосвязи 'link'. В общем случае вектор коэффициентов регрессионной модели b рассчитывается с помощью функции glmfit.
Входной аргумент 'link' задает вид взаимосвязи между параметром распределения и оцениваемой линейной комбинацией независимых переменных ![]() . Параметр 'link' задается в соответствии с требованиями к такому же входному аргументу функции glmfit. Предусмотрены следующие значения 'link'
. Параметр 'link' задается в соответствии с требованиями к такому же входному аргументу функции glmfit. Предусмотрены следующие значения 'link'
|
Значение 'link' |
Вид зависимости |
|
'identity' |
µ = xb |
|
'log' |
log(µ) = xb |
|
'logit' |
log(µ/ (1-µ)) = xb |
|
'probit' |
norminv(µ) = xb |
|
'comploglog' |
log(-log(1-µ)) = xb |
|
'logloglink' |
log(-log(µ)) = xb |
|
'reciprocal' |
1/µ = xb |
|
p (число) |
µp = xb |
Кроме приведенных выше значений ' link ' возможно задать произвольный вид зависимости с помощью inline функций или m-файлов. Правила и примеры использования такого способа см. в описании функции glmfit.
Выходной параметр yfit является значением обратной функции взаимосвязи линейной комбинации ![]() .
.
[yfit,dlo,dhi] = glmval(b,X,'link',stats,clev) в этом варианте синтаксиса функция возвращает нижнее dlo и верхнее dhi отклонения от yfit границ доверительного интервала параметров закона распределения для заданных b, X, 'link'. Для расчета dlo, dhi используется структура stats, полученная как выходной параметр функции glmfit. Входной параметр clev задает доверительную вероятность для расчета границ доверительного интервала. По умолчанию clev принимается равной 0.95, что соответствует 95% доверительному интервалу. Границы доверительного интервала рассчитываются как [yfit-dlo, yfit+dhi].
[yhat,dlo,dhi] = glmval(beta,X,'link',stats,clev,N,offset,'const') дополнительные входные параметры N, offset, 'const' требуются для обеспечения одинаковых условий с расчетами, проводимыми при помощи функции glmfit. При использовании биномиального закона при работе с glmfit, необходимо задать входной параметр N соответствующий числу повторных независимых испытаний. Если при вызове функции glmfit использовались параметры offset и 'const', то необходимо при вызове функции glmval использовать эти же параметры с теми же значениями.
Примеры использования функции расчета значений зависимой переменной обобщенной регрессионной модели
Рассчитывается значение зависимой переменной, среднего арифметического, yfit для значений независимой переменной xnew. В качестве модели распределения зависимой переменной принят нормальный закон. Вид взаимосвязи среднего арифметического от линейной модели независимой переменой принята логарифмическая зависимость: log(µ) = xb. Также рассчитываются границы 95% доверительного интервала зависимой переменой.
>> x = 1:1:10;
>> y = 1:2:20;
>> y1 = normrnd(0,1,10,1);
>> y = y.^2+y1';
>> [b,dev,stats] = glmfit(x,y,'normal', 'log')
b =
2.8832
0.3057
dev =
2.9747e+003
stats =
beta: [2x1 double]
dfe: 8
sfit: 19.2832
estdisp: 1
s: 19.2832
se: [2x1 double]
coeffcorr: [2x2 double]
t: [2x1 double]
p: [2x1 double]
resid: [10x1 double]
residp: [10x1 double]
residd: [10x1 double]
resida: [10x1 double]
>> xnew = 0.5:1:10;
>> [yfit,ylo,yhi] = glmval(b,xnew, 'log',stats,0.95)
yfit =
20.8229
28.2695
38.3792
52.1042
70.7376
96.0346
130.3783
177.0039
240.3036
326.2403
ylo =
7.3595
9.0451
10.9368
12.9484
14.9096
16.5393
17.4771
17.6222
18.7130
26.9608
yhi =
11.3823
13.3008
15.2954
17.2303
18.8914
19.9804
20.1826
19.5706
20.2933
29.3896
>> errorbar(xnew,yfit,ylo,yhi);
>> grid on
>> plot(x,y, 's', xnew,yfit, 'r', xnew, yfit-ylo, 'b', xnew, yfit+yhi, 'b');
>> grid on
Сравниваются линейная - и квадратическая - ![]() модели.
модели.
>> [b2,dev2,stats2] = glmfit([x' x.^2'],y,'normal', 'log')
b2 =
1.4019
0.7277
-0.0280
dev2 =
228.0208
stats2 =
beta: [3x1 double]
dfe: 7
sfit: 5.7074
estdisp: 1
s: 5.7074
se: [3x1 double]
coeffcorr: [3x3 double]
t: [3x1 double]
p: [3x1 double]
resid: [10x1 double]
residp: [10x1 double]
residd: [10x1 double]
resida: [10x1 double]
>> [yfit2,ylo2,yhi2] = glmval(b2, [xnew' xnew.^2'], 'log',stats2,0.95)
yfit2 =
5.8050
11.3639
21.0349
36.8163
60.9297
95.3469
141.0825
197.3915
261.1393
326.6667
ylo2 =
2.2079
3.4240
4.7618
5.8614
6.3310
6.2166
6.5167
7.7613
8.2410
8.6649
yhi2 =
3.5630
4.9005
6.1551
6.9713
7.0651
6.6502
6.8322
8.0790
8.5095
8.9010
>> plot(x,y, 's', xnew,yfit, 'r:', xnew, yfit-ylo, 'b', xnew, yfit+yhi, 'b', xnew,yfit2, 'g:', xnew, yfit2-ylo2, 'y', xnew, yfit2+yhi2, 'y-');
>> grid on
Рассматривается пример моделирования числа автомобилей с низким расходом топлива на основе биномиального закона. Сначала биномиальный закон используется для моделирования вероятности получить низкий расход топлива как функцию от первого порядка массы и квадрата массы автомобиля. По умолчанию вид зависимости задается как logit. Затем рассчитывается вектор wnew задающий массу автотранспортных средств, для которых будет рассчитываться зависимая переменная. Далее рассчитывается ожидаемое количество автомобилей из общего числа равного 30 для каждой группы с заданной массой, которые будут иметь низкий расход топлива. В конце графически отображаются значения зависимой переменной и 95% границы доверительного интервала как функции от массы автомобиля.
>> w = [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]';
>> poor = [1 2 0 3 8 8 14 17 19 15 17 21]';
>> total = [48 42 31 34 31 21 23 23 21 16 17 21]';
>> [b2,d2,s2] = glmfit([w w.^2],[poor total],'binomial')
b2 =
-7.3109
0.0002
0.0000
d2 =
5.7815
s2 =
beta: [3x1 double]
dfe: 9
sfit: 0.6556
estdisp: 0
s: 1
se: [3x1 double]
coeffcorr: [3x3 double]
t: [3x1 double]
p: [3x1 double]
resid: [12x1 double]
residp: [12x1 double]
residd: [12x1 double]
resida: [12x1 double]
>> wnew = (3000:100:4000)';
>> [yfit,dlo,dhi] = glmval(b2,[wnew wnew.^2],'logit',s2,0.95,30)
yfit =
8.3957
11.1060
14.2168
17.4916
20.6232
23.3399
25.4935
27.0736
28.1626
28.8776
29.3296
dlo =
2.4741
2.9335
3.2301
3.2985
3.1920
3.0263
2.8588
2.6753
2.4562
2.2064
1.9456
dhi =
3.0179
3.2920
3.3047
3.0680
2.6923
2.2845
1.8780
1.4737
1.0918
0.7636
0.5072
>> errorbar(wnew,yfit,dlo,dhi);
leverage - Оценка степени влияния отдельных наблюдений в исходном многомерном множестве данных на значения параметров линии регрессии.
Синтаксис
h = leverage(data)
h = leverage(data,'model')
Описание
h = leverage(data) функция позволяет оценить коэффицинты влияния h каждого из наблюдений, строк в матрице data, на коэффициенты линейного уравнения регрессии. Выходной параметр h определяется как вектор length(h)=size(data,1).
h = leverage(data,'model') функция предназначена для оценки коэффициентов влияния отдельных наблюдений на коэффициенты полиномиальной регрессионной модели, определяемой входным параметром 'model'. Предусмотрены следующие виды регрессионных моделей:
-
'linear' - линейная модель, включает линейные эффекты независимых переменных и постоянный член;
-
'interaction' - модель взаимодействий, включающая линейные эффекты, эффекты взаимодействий независимых переменных и постоянный член.
-
'quadratic' - квадратическая модель, включает эффекты взаимодействий и квадратические эффекты независимых переменных;
-
'purequadratic' - квадратическая модель без учета эффектов взаимодействий независимых переменных, включает линейные, квадратические эффекты и постоянный член.
Коэффициенты влияния h на параметры полиномиальной регрессионной модели определяются с учетом положения каждого из наблюдений в пространстве независимых переменных.
Алгоритм расчета коэффициентов влияния
[Q,R] = qr(x2fx(data,'model'));
leverage = (sum(Q'.*Q'))'
Примеры использования функции leverage
1. Сравнение коэффициентов влияния наблюдений нормально распределенной двумерной случайной величины без выбросов и с выбросами в выборке для линейной модели.
1.1. Моделирование матрицы независимых случаных величин, распределенных по нормальному закону с нулевым математическим ожиданием и единичной дисперсией
>> r=normrnd(0,1,10,2)
r =
-0.1867 0.2944
0.7258 -1.3362
-0.5883 0.7143
2.1832 1.6236
-0.1364 -0.6918
0.1139 0.8580
1.0668 1.2540
0.0593 -1.5937
-0.0956 -1.4410
-0.8323 0.5711
1.2. Расчет коэффициентов влияния наблюдений
>> h = leverage(r)
h =
0.1432
0.3559
0.2940
0.6896
0.1462
0.1710
0.2640
0.3140
0.2689
0.3532
1.3. Добавление выбороса в последнее наблюдение
>> r(10,1)=10;r(10,2)=-10;
1.4. Расчет коэффициентов влияния наблюдений
>> h1 = leverage(r,'linear')
h1 =
0.1253
0.1323
0.1404
0.5810
0.1630
0.1402
0.2679
0.2347
0.2380
0.9773
2. Сравнение коэффициентов влияния наблюдений нормально распределенной двумерной случайной величины без выбросов и с выбросами в выборке для квадратической модели.
2.1. Моделирование матрицы 3-х независимых случаных величин, распределенных по нормальному закону с нулевым математическим ожиданием и единичной дисперсией
>> r=normrnd(0,1,10,3);
>> r=r.^2
r =
0.1599 2.5731 1.0214
0.4761 0.0662 0.3776
0.6652 1.1161 0.2578
0.5068 2.0026 2.8643
1.6647 0.6482 0.3496
0.4470 0.2796 0.4142
1.4181 0.0481 0.1447
1.4459 0.8499 1.0183
0.0004 4.7118 0.0004
0.0246 0.0035 0.0023
2.2. Расчет коэффициентов влияния наблюдений
>> h = leverage(r,'purequadratic' )
h =
0.7615
0.4837
0.9105
0.9983
0.6530
0.3259
0.4372
0.5627
0.9866
0.8806
2.3. Добавление выбороса в последнее наблюдение
>> r(10,1)=10;r(10,2)=-10; r(10,3)=-5;
2.4. Расчет коэффициентов влияния наблюдений
>> h1 = leverage(r1, 'purequadratic')
h1 =
0.2776
0.4268
0.5176
0.8139
0.3702
0.3366
0.5810
0.4042
0.2724
0.9998
Как следует из полученных результатов, внесение выброса в исходную выборку приводит к увеличению коэффициента влияния измененного значения за счет уменьшения значений h других наблюдений.
lscov - Линейная регрессия (метод наименьших квадратов) при заданной матрице ковариаций (встроенная функция MATLAB)
Синтаксис
x = lscov(A,b,V)
[x,dx] = lscov(A,b,V)
Описание
x = lscov(A,b,V) функции возвращает вектор х, являющийся решением системы уравнений A*x=b+e, где e - вектор нормально распределенных значений погрешностей с нулевым математическим ожиданием и ковариацией V. В рассматриваемой задаче метод наименьших квадратов применяется для решения переопределенной системы уравнений. Размерность матрицы A - m?n, где m - количество наблюдений, n - число независимых переменных, m>n. Размерность матрицы V равна m?m. Матрица V должна быть положительно определенной.
[x,dx] = lscov(A,b,V) функция предназначена для расчета вектора решений x системы уравнений A*x=b+e и их стандартных ошибок dx. Размерность векторов x и dx будет совпадать.
Алгоритм
Вектор х находится из условия минимизации выражения
(A*x-b)'*inv(V)*(A*x-b).
Классическое решение этой задачи, известное из линейной алгебры, имеет следующий вид
x = inv(A'*inv(V)*A)*A'*inv(V)*b.
В функции lscov использована QR декомпозиция матрицы А с последующей модификацией величины Q по заданной ковариации V.
Величины стандартных ошибок рассчитываются по формулам:
mse = B'*(inv(V)-inv(V)*A*inv(A'*inv(V)*A)*A'*inv(V))*B./(m-n)
dx = sqrt(diag(inv(A'*inv(V)*A)*mse)).
Примеры использования функции lscov
1. Решение переопределенной системы уравенений методом наименьших квадратов.
1.1. Моделирование матрицы наблюдений независимых переменных
>> A1=unidrnd(10,10,1);
>> A=[A1 ones(10,1)]
A =
10 1
3 1
7 1
5 1
9 1
8 1
5 1
1 1
9 1
5 1
1.2. Моделирование вектора наблюдений зависимой переменной
>> b=A(:,1)*0.5+ A(:,2) *0.2+normrnd(0,1,10,1)
b =
5.2000
1.3821
4.7950
0.8260
5.1282
5.0956
3.4310
1.2779
4.7403
3.3771
1.3. Моделирование ковариационной матрицы
>> V= normrnd(0,1,10,10);
1.4. Решение системы уравнений
>> x = lscov(A,b,V)
x =
0.2561
1.4567
2. Расчет вектора решений переопределенной системы уравенений
и их стандартных ошибок методом наименьших квадратов.
2.1. Моделирование матрицы наблюдений независимых переменных
>> A1=unidrnd(10,10,2);
>> A=[A1 ones(10,1)]
A =
7 1 1
8 4 1
10 9 1
8 1 1
2 2 1
5 3 1
10 2 1
10 7 1
5 3 1
9 2 1
2.2. Моделирование вектора наблюдений зависимой переменной
>> b=A(:,1)*0.5+ A(:,2) *0.2- A(:,3)+normrnd(0,1,10,1)
b =
3.7184
2.2196
5.7213
2.5183
-0.6246
0.8656
4.6888
4.9707
2.1558
3.5321
2.3. Моделирование ковариационной матрицы
>> V= pascal(10)./max(max( pascal(10)));
2.4. Расчет вектора решений и их стандартных ошибок
>> [x,dx] = lscov(A,b,V)
x =
-0.0428
0.0787
3.9392
dx =
0.0475
0.0606
11.4383
multcompare - Множественной сравнение оценок средних, параметров линии регрессии и т.д. В качестве входных параметров используются выходные параметры функций anova1, anova2, anovan, aoctool, friedman, kruskalwallis.
Синтаксис
c = multcompare(stats)
c = multcompare(stats,alpha)
c = multcompare(stats,alpha,'displayopt')
c = multcompare(stats,alpha,'displayopt','ctype')
c = multcompare(stats,alpha,'displayopt','ctype','estimate')
c = multcompare(stats,alpha,'displayopt','ctype','estimate',dim)
[c,m] = multcompare(...)
[c,m,h] = multcompare(...)
Описание
c = multcompare(stats) функция предназначена проверки параметрических гипотез при парном сравнении средних арифметических или других оценок на основе информации в структуре данных stats. Выходным параметром является матрица с результатами проверки параметрических гипотез. Также функция позволяет построить интерактивный график по результатам проверки множества параметрических гипотез.
При проведении дисперсионного анализа по множеству выборок проверяется нулевая гипотеза, состоящая в том, что все выборочные средние арифметические равны между собой, выборки извлечены из одной генеральной совокупности или из нескольких генеральных совокупностей с одинаковыми значениями средних арифметических. Альтернативная гипотеза состоит в том, что значение хотя бы одного выборочного среднего арифметического отличается от остальных.
После проведения дисперсионного анализа целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие. Для проверки такой параметрической гипотезы используется процедура множественного сравнения.
При проверке простой параметрической гипотезы (нулевой гипотезы) о равенстве средних одной группы выборок по отношению к другой по статистике t необходимо задать уровень значимости ![]() , определяющий критическое значение статистики
, определяющий критическое значение статистики![]() . В большинстве практических случаев
. В большинстве практических случаев ![]() принимают равным 0,05; 0,01. Это означает, что в 5%, или 1% случаев будет неверно отвергнута нулевая гипотеза. При увеличении групп выборок, увеличивается число проверяемых гипотез. При использовании простой параметрической гипотезы по статистике t, уровень значимости
принимают равным 0,05; 0,01. Это означает, что в 5%, или 1% случаев будет неверно отвергнута нулевая гипотеза. При увеличении групп выборок, увеличивается число проверяемых гипотез. При использовании простой параметрической гипотезы по статистике t, уровень значимости ![]() будет применяться к каждой гипотезе отдельно, что повлечет к росту вероятности неверно отвергнуть нулевую гипотезу пропорционально количеству выполненных проверок. Т.е., неверно определить значимое отличие выборочных средних. Процедура множественного сравнения обеспечивает заданный уровень значимости для каждой проверки.
будет применяться к каждой гипотезе отдельно, что повлечет к росту вероятности неверно отвергнуть нулевую гипотезу пропорционально количеству выполненных проверок. Т.е., неверно определить значимое отличие выборочных средних. Процедура множественного сравнения обеспечивает заданный уровень значимости для каждой проверки.
Выходной параметр с представляет результаты множественного сравнения в виде матрицы из 5 столбцов. Срока матрицы с соответствуют результатам проверки одной параметрической гипотезы. Таким образом, каждая строка с соответствует одной паре выборок. Первые два значения в строке с показывают номера сравниваемых выборок, третий - величину разности средних арифметических сравниваемых выборок, четвертый и пятый столбцы - 95% доверительный интервал полученной разности средних арифметических.
Например, если строка с содержит следующие значения:
2.0000 5.0000 1.9442 8.2206 14.4971
полученные значения показывают, что сравниваются средние арифметические значения 2 и 5 выборок, величина их разности равна 1.9442, 95% доверительный интервал полученной разности средних арифметических составил [1.9442, 14.4971]. Поскольку в доверительный интервал не попало нулевое значение, следовательно разность средних арифметических 2 и 5 выборок значима. Т.е. средние арифметические выборок статистически значимо отличаются друг от друга, для ![]() .
.
Функция multcompare позволяет графически отобразить значения средних арифметических и их доверительных интервалов. Два выборочных средних значимо отличаются, если их доверительные интервалы не пересекаются на графике. При наложении границ доверительных интервалов двух средних арифметических, различие между ними можно считать статистически незначимым. По графику можно определить выборки со средними арифметическими, которые значимо отличающиеся от интересующего выборочного среднего. Для этого необходимо мышью выделить график интересующего выборочного среднего. Соответствующие графики будут выделены другим цветом.
c = multcompare(stats,alpha) такой вариант синтаксиса функции позволяет задать уровень значимости alpha для расчета доверительных интервалов разностей средних арифметических представленных в матрице с. Доверительная вероятность определяется как 100*(1-alpha)%. Значение по умолчанию alpha=0,05.
c = multcompare(stats,alpha,'displayopt') входной аргумент 'displayopt' позволяет отобразить график с результатами множественного сравнения 'displayopt'='on', или подавить вывод графика 'displayopt'='off'. Значение по умолчанию 'displayopt'='on'.
c = multcompare(stats,alpha,'displayopt','ctype') входной аргумент 'ctype' позволяет задать способ определения критических значений статистик при проверке нулевой гипотезы. Предусмотрены следующие значения 'ctype':
|
Значение 'ctype' |
Способ определения критических значений статистик |
|
'hsd', или 'tukey-kramer' |
Используется разностный критерий Тьюки. Значение по умолчанию. Критерий основан на распределении выборочного размаха по закону Стьюдента. Критерий является оптимальным для однофакторного дисперсионного анализа и аналогичных процедур для выборок с равным объемом. Доказана его ограниченна применимость для однофакторного дисперсионного анализа с разным объемом выборок. |
|
'lsd' |
Используется процедура определения критических значений статистики по наименее значимой разности критерия Тьюки. Эта процедура основана на использовании простого t теста. Она приемлема, если предварительный тест (имеется в виду F статистика при однофакторном дисперсионном анализе) показала значимое различие сравниваемых средних. |
|
'bonferroni' |
Основан на расчете критических значений распределения Стьюдента с корректировкой Бонферони для использования в процедуре множественного сравнения. |
|
'dunn-sidak' |
Используются критические значения рассчитанные по распределению Стьюдента после корректировки для процедуры множественного сравнения предложенной Данном. |
|
'scheffe' |
Используются критические значения рассчитанные по процедуре Шеффе, основанной на распределении Фишера. Эта процедура позволяет обеспечивает одинаковый уровень значимости при сравнении линейных комбинаций средних. |
c = multcompare(stats,alpha,'displayopt','ctype','estimate') входной аргумент 'estimate' позволяет задать вид оценок используемых в процедуре множественного сравнения. Возможные виды оценок определяются функцией, использованной для расчета структуры stats, и приведены в следующей таблице:
|
Функция |
Значения 'estimate' |
|
'anova1' |
Значения 'estimate' игнорируются. Всегда сравниваются средние по группам. |
|
'anova2' |
'estimate'='column' (значение по умолчанию) - для сравнения средних по столбцам, 'estimate'='row' - для сравнения средних по строкам. |
|
'anovan' |
Значения 'estimate' игнорируются. Всегда сравниваются маргинальные средние генеральной совокупности, определяемые согласно аргументу dim. |
|
'aoctool' |
'estimate'='slope', 'intercept', 'pmm' для сравнения значений начального смещения, коэффициентов при первой степени независимой переменной, маргинальных средних генеральной совокупности. Если модель корреляционного анализа не включает разделенные постоянные смещения, тогда использовать значение 'estimate'='slope' запрещено. Также невозможно применить значение 'estimate'='intercept', если нет разделенных коэффициентов при линейной степени независимой переменной модели. |
|
'friedman' |
Значения игнорируются. Всегда сравниваются средние по столбцам. |
|
'kruskalwallis' |
Значения игнорируются. Всегда сравниваются средние по группам. |
c = multcompare(stats,alpha,'displayopt','ctype','estimate',dim) входной аргумент dim задает маргинальные средние распределений подлежащие сравнению. Этот аргумент необходим, если при расчете stats использовалась функция anovan. При проведении многофакторного дисперсионно анализа с n факторами, dim может быть задан как скаляр или вектор целых чисел в диапазоне от 1 до n. Значение по умолчанию dim=1.
Например, если dim=1 сравниваемые точечные оценки являются средними арифметическими групп, определяемых значениями первой группирующей переменной, скорректированных удалением эффектов других группирующих переменных, как если бы план был сбалансирован, т.е. заданы выборки одинакового объема. Если dim=[1 3], маргинальные средние распределений вычисляются для каждой комбинации первой и третьей группирующих переменных, с игнорированием эффектов второй группирующей переменной. Если используется сингулярная модель, средние арифметические по некоторым группам не могут быть рассчитаны и соответствующие им маргинальные средние примут значение NaN.
[c,m] = multcompare(...) функция возвращает матрицу m точечных и интервальных оценок средних арифметических значений или других сравниваемых оценок. Первый столбец матрицы m содержит точечные оценки средних арифметических, или сравниваемых статистик, для каждой группы. Второй столбец m содержит величины стандартных ошибок сравниваемых оценок.
[c,m,h] = multcompare(...) функция возвращает указатель h на график, сформированный в результате множественного сравнения. Следует отметить, что в строке заголовка графика выводится инструкции по работе с интерактивным графиком, подписи по оси абсцисс содержат список групп, у которых средние арифметические значимо отличаются от среднего арифметического для выделенного графика. Для удаления заголовка графика и подписи по оси Х необходимо использовать интерактивные инструменты графического окна или команды:
>> title('')
>> xlabel('')
Примеры использования функции множественного сравнения выборочных средних арифметических и других оценок
Однофакторный дисперсионный анализ для пяти выборок с математическими ожиданиями, изменяющимися в пределах от 1 до 5, с последующим проведением множественного сравнения оценок средних арифметических.
>> X = meshgrid(1:5);
>> X = X + normrnd(0,1,5,5);
>> group = ['Aa'; 'Bb'; 'Cc'; 'Dd'; 'Ee'];
>> [p,table,stats] = anova1(X, group);
>> c = multcompare(stats)
c =
1.0000 2.0000 -3.8426 -2.1352 -0.4277
1.0000 3.0000 -4.6733 -2.9658 -1.2584
1.0000 4.0000 -5.3362 -3.6287 -1.9213
1.0000 5.0000 -6.3946 -4.6872 -2.9797
2.0000 3.0000 -2.5381 -0.8306 0.8768
2.0000 4.0000 -3.2010 -1.4935 0.2139
2.0000 5.0000 -4.2594 -2.5520 -0.8445
3.0000 4.0000 -2.3703 -0.6629 1.0446
3.0000 5.0000 -3.4288 -1.7214 -0.0139
4.0000 5.0000 -2.7659 -1.0585 0.6490
Двухфакторный дисперсионный анализ для шести уровней по первому фактору, двум уровням и 3-х повторений по второму фактору, с последующим проведением множественного сравнения оценок средних арифметических при 99% доверительном интервале (![]() ).
).
>> X = normrnd(0,1,6,6);
>> [p,table,stats] = anova2(X,3);
>> alpha = 0.01;
>> c = multcompare(stats,alpha)
Note: Your model includes an interaction term. A test of main
effects can be difficult to interpret when the model includes
interactions.
c =
1.0000 2.0000 -2.9346 -1.0198 0.8951
1.0000 3.0000 -1.4097 0.5051 2.4200
1.0000 4.0000 -1.7510 0.1638 2.0787
1.0000 5.0000 -2.4294 -0.5146 1.4002
1.0000 6.0000 -1.8167 0.0981 2.0129
2.0000 3.0000 -0.3899 1.5249 3.4397
2.0000 4.0000 -0.7312 1.1836 3.0984
2.0000 5.0000 -1.4096 0.5052 2.4200
2.0000 6.0000 -0.7970 1.1179 3.0327
3.0000 4.0000 -2.2561 -0.3413 1.5735
3.0000 5.0000 -2.9346 -1.0197 0.8951
3.0000 6.0000 -2.3219 -0.4070 1.5078
4.0000 5.0000 -2.5933 -0.6784 1.2364
4.0000 6.0000 -1.9806 -0.0657 1.8491
5.0000 6.0000 -1.3021 0.6127 2.5275
Однофакторный дисперсионный анализ для пяти выборок с математическими ожиданиями, изменяющимися в пределах от 1 до 5, с последующим проведением множественного сравнения оценок средних арифметических при 99% доверительном интервале (![]() ). При расчете критического уровня статистики используется процедура по наименее значимой разности критерия Тьюки.
). При расчете критического уровня статистики используется процедура по наименее значимой разности критерия Тьюки.
>> X = meshgrid(1:5);
>> X = X + normrnd(0,1,5,5);
>> group = ['Aa'; 'Bb'; 'Cc'; 'Dd'; 'Ee'];
>> [p,table,stats] = anova1(X, group);
>> alpha = 0.01;
>> displayopt='on';
>> ctype='lsd';
>> c = multcompare(stats,alpha,displayopt,ctype)
c =
1.0000 2.0000 -2.8283 -1.4736 -0.1190
1.0000 3.0000 -2.7817 -1.4270 -0.0723
1.0000 4.0000 -4.7391 -3.3844 -2.0297
1.0000 5.0000 -5.5488 -4.1942 -2.8395
2.0000 3.0000 -1.3080 0.0467 1.4013
2.0000 4.0000 -3.2655 -1.9108 -0.5561
2.0000 5.0000 -4.0752 -2.7205 -1.3659
3.0000 4.0000 -3.3121 -1.9574 -0.6028
3.0000 5.0000 -4.1219 -2.7672 -1.4125
4.0000 5.0000 -2.1644 -0.8097 0.5449
Выполняется многофакторный дисперсионный анализ для 3-х факторов изменяющихся двух уровнях, с последующим множественным сравнением при 99% доверительном интервале (![]() ).При расчете критического уровня статистики используется процедура Шеффе. маргинальные средние распределений подлежащие сравнению заданы переменной dim=[1 3]. Маргинальные средние распределений вычисляются для каждой комбинации первой и третьей группирующих переменных, удаляя эффекты второй группирующей переменной.
).При расчете критического уровня статистики используется процедура Шеффе. маргинальные средние распределений подлежащие сравнению заданы переменной dim=[1 3]. Маргинальные средние распределений вычисляются для каждой комбинации первой и третьей группирующих переменных, удаляя эффекты второй группирующей переменной.
>> X=normrnd(0,1,8,1);
>> group = {[1 2 1 2 1 2 1 2]; ['hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo']; {'may' 'may' 'may' 'may' 'june' 'june' 'june' 'june'}};
>> [p,table,stats,terms] = anovan(X,group);
>> alpha = 0.01;
>> displayopt='on';
>> ctype='scheffe';
>> estimate =1;
>> dim=[1 3];
>> c = multcompare(stats,alpha,displayopt,ctype,estimate,dim)
c =
1.0000 2.0000 -4.0683 0.2935 4.6554
1.0000 3.0000 -4.3823 -0.0205 4.3414
1.0000 4.0000 -5.8955 0.2731 6.4416
2.0000 3.0000 -6.4825 -0.3140 5.8546
2.0000 4.0000 -4.3823 -0.0205 4.3414
3.0000 4.0000 -4.0683 0.2935 4.6554
Однофакторный дисперсионный анализ для пяти выборок с математическими ожиданиями, изменяющимися в пределах от 1 до 5, с последующим проведением множественного сравнения оценок средних арифметических. Функция возвращает матрицу m точечных и интервальных оценок средних арифметических значений и указатель на график множественного сравнения.
>> X = meshgrid(1:5);
>> X = X + normrnd(0,1,5,5);
>> group = ['Aa'; 'Bb'; 'Cc'; 'Dd'; 'Ee'];
>> [p,table,stats] = anova1(X, group);
>> [c,m,h] = multcompare(stats)
c =
1.0000 2.0000 -2.0501 -0.3580 1.3341
1.0000 3.0000 -3.4140 -1.7219 -0.0298
1.0000 4.0000 -4.4701 -2.7780 -1.0859
1.0000 5.0000 -4.8882 -3.1961 -1.5040
2.0000 3.0000 -3.0561 -1.3640 0.3281
2.0000 4.0000 -4.1121 -2.4200 -0.7279
2.0000 5.0000 -4.5302 -2.8381 -1.1460
3.0000 4.0000 -2.7481 -1.0560 0.6361
3.0000 5.0000 -3.1663 -1.4742 0.2179
4.0000 5.0000 -2.1102 -0.4181 1.2740
m =
1.0044 0.3998
1.3624 0.3998
2.7264 0.3998
3.7824 0.3998
4.2005 0.3998
h =
2
polyconf - Определение доверительных интервалов для линии регрессии
Синтаксис
[Y,DELTA] = polyconf(p,X,S)
[Y,DELTA] = polyconf(p,X,S,alpha)
Описание
[Y,DELTA] = polyconf(p,X,S) функция позволяет рассчитать значения зависимой переменой Y однофакторной регрессионной полиномиальной модели произвольного порядка в заданных точках X. Коэффициенты регрессионной модели задаются вектором р.
Вектор коэффициентов p содержит n+1 элемент, расположенных по убыванию степени независимой переменной согласно формуле:
![]()
где n - порядок полинома. Входной аргумент S рассчитывается с использованием функции polyfit. Результаты расчета значений зависимой переменной могут быть представлены как Y±DELTA, где DELTA соответствует 95% доверительному интервалу. При расчете DELTA предполагается, что отклонения значений зависимой переменной y от регрессионной модели независимы и распределены по нормальному закону с постоянной дисперсией.
[Y,DELTA] = polyconf(p,X,S,alpha) функция позволяет рассчитать границы доверительного интервала DELTA соответствующие уровню значимости alpha. Доверительная вероятность определяется как 100(1-alpha)%.
Входной аргумент Х может быть задан как вектор или матрица. Значения регрессионной модели рассчитываются для каждого элемента Х. Размерность Х, Y и DELTA будет одинаковой.
Примеры использования функции расчета значений однофакторной полиномиальной регрессионной модели произвольного порядка
Расчет значений линейной модели и их 95% доверительных интервалов
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x+d;
>> [p S] = polyfit(x,y,1)
p =
1.3378 -1.7450
S =
R: [2x2 double]
df: 8
normr: 3.6995
>> X = 0:2:20;
>> [Y,DELTA] = polyconf(p,X,S)
Y =
Columns 1 through 7
-1.7450 0.9307 3.6063 6.2820 8.9577 11.6334 14.3091
Columns 8 through 11
16.9848 19.6605 22.3362 25.0119
DELTA =
Columns 1 through 7
3.6528 3.3702 3.2024 3.1678 3.2706 3.4986 3.8297
Columns 8 through 11
4.2396 4.7080 5.2190 5.7613
>> f=p(1)*X+ p(2);
>> plot(X,Y,'+',x,y,'o',X,f)
>> grid on
Расчет значений квадратической модели и их 99% доверительных интервалов
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x.^2/5+d;
>> [p S] = polyfit(x,y,2)
p =
0.2601 -0.6233 1.1314
S =
R: [3x3 double]
df: 7
normr: 4.1858
>> X = 0:1.2:12;
>> alpha = 0.01;
>> [Y,DELTA] = polyconf(p,X,S,alpha)
Y =
Columns 1 through 7
1.1314 0.7580 1.1335 2.2580 4.1314 6.7537 10.1251
Columns 8 through 11
14.2454 19.1146 24.7328 31.0999
DELTA =
Columns 1 through 7
8.5473 6.8320 6.1153 6.0258 6.1153 6.1259 6.0382
Columns 8 through 11
6.0700 6.6497 8.1858 10.7948
>> Y_min=Y-DELTA;
>> Y_max=Y+DELTA;
>> f=p(1)*X.^2+ p(2).* X + p(3);
>> plot(X,Y,'+', X, Y_min,X,Y_max,x,y,'o',X,f)
>> grid on
Расчет значений квадратической модели и
их 99% доверительных интервалов для матрицы значений Х.
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x.^2/5+d;
>> [p S] = polyfit(x,y,2)
p =
0.2601 -0.6233 1.1314
S =
R: [3x3 double]
df: 7
normr: 4.1858
>> X = magic(3)
X =
8 1 6
3 5 7
4 9 2
>> alpha = 0.01;
>> [Y,DELTA] = polyconf(p,X,S,alpha)
Y =
12.7887 0.7682 6.7537
1.6021 4.5164 9.5112
2.7992 16.5863 0.9251
DELTA =
6.0227 7.0429 6.1259
6.0227 6.1259 6.0535
6.0535 6.2609 6.2609
polyfit - Полиномиальная регрессия (встроенная функция MATLAB)
Синтаксис
[p,S] = polyfit(x,y,n)
Описание
p = polyfit(x,y,n) функция позволяет рассчитать коэффициенты p полиномиальной регрессионной модели n-й степени для выборки x, y методом наименьших квадратов, где x - независимая переменная, y - зависимая переменная. Зависимая и независимая переменные задаются как векторы с одинаковым числом элементов. Вектор коэффициентов p содержит n+1 элемент, расположенных по убыванию степени независимой переменной согласно формуле:
![]()
[p,S] = polyfit(x,y,n) функция возвращает коэффициенты p полиномиальной регрессионной модели n-й степени и матрицы S для выборки x, y. S используется в качестве входного аргумента функции polyval для расчета границ доверительного интервала значений полиномиальной регрессионной модели в заданных точках. Если отклонения значений зависимой переменной y от регрессионной модели независимы и распределены по нормальному закону с постоянной дисперсией, границы доверительного интервала, полученные polyval, включают как минимум 50% рассчитанных значений.
polyfit является стандартной функцией MATLAB.
Примеры использования функции расчета коэффициентов однофакторной регрессионной полиномиальной модели произвольного порядка
Расчет коэффициентов линейной модели
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x+d;
>> p = polyfit(x,y,1)
p =
1.0000 -0.4326
>> f=p(1)*x+ p(2);
>> plot(x,y,'+',x,f)
>> grid on
Расчет коэффициентов квадратической модели и матрицы S
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x.^2+d;
>> [p S] = polyfit(x,y,2)
p =
1.0512 -0.6534 0.9738
S =
R: [3x3 double]
df: 7
normr: 6.1614
>> S.R
ans =
-159.1634 -19.0056 -2.4189
0 -4.8771 -1.8510
0 0 0.8502
>> f=p(1)*x.^2+ p(2).*x+ p(3);
>> plot(x,y,'+',x,f)
>> grid on
polyval - Прогноз с использованием полиномиальной регрессии (встроенная функция MATLAB)
Синтаксис
Y = polyval(p,X)
[Y,DELTA] = polyval(p,X,S)
Описание
Y = polyval(p,X) функция позволяет рассчитать значения зависимой переменной Y однофакторной регрессионной полиномиальной модели произвольного порядка в заданных точках независимой переменной X. Коэффициенты регрессионной модели задаются вектором р.
Вектор коэффициентов p содержит n+1 элемент, расположенных по убыванию степени независимой переменной согласно формуле:
![]()
где n - порядок полинома.
[Y,DELTA] = polyval(p,X,S) функция позволяет рассчитать значения Y однофакторной регрессионной полиномиальной модели произвольного порядка и границы 95% доверительного интервала DELTA в заданных точках X. Результаты расчета значений зависимой переменной могут быть представлены как Y±DELTA. Входной аргумент S рассчитывается с использованием функции polyfit. Если отклонения значений зависимой переменной y от регрессионной модели независимы и распределены по нормальному закону с постоянной дисперсией, границы доверительного интервала, полученные polyval, включают как минимум 50% рассчитанных значений.
Входной аргумент Х может быть задан как вектор или матрица. Значения регрессионной полиномиальной модели рассчитываются для каждого элемента Х. Размерность Х, Y и DELTA будет одинаковой.
polyval является стандартной функцией MATLAB.
Примеры использования функции расчета значений однофакторной регрессионной полиномиальной модели произвольного порядка
Расчет значений линейной модели
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x+d;
>> [p S] = polyfit(x,y,1)
p =
0.7334 1.6928
S =
R: [2x2 double]
df: 8
normr: 3.7728
>> X = 0:2:20;
>> Y = polyval(p,X)
Y =
Columns 1 through 7
1.6928 3.1597 4.6266 6.0934 7.5603 9.0272 10.4940
Columns 8 through 11
11.9609 13.4277 14.8946 16.3615
>> f=p(1)*X+ p(2);
>> plot(X,Y,'+',x,y,'o',X,f)
>> grid on
Расчет значений квадратической модели и их 95% доверительных интервалов
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x.^2+d;
>> [p S] = polyfit(x,y,2)
p =
0.9491 0.6023 -0.7749
S =
R: [3x3 double]
df: 7
normr: 4.9811
>> X = 0:1.2:12;
>> [Y DELTA] = polyval(p,X,S)
Y =
Columns 1 through 7
-0.7749 1.3145 6.1372 13.6933 23.9826 37.0053 52.7613
Columns 8 through 11
71.2507 92.4734 116.4294 143.1187
DELTA =
Columns 1 through 7
2.9065 2.3232 2.0795 2.0490 2.0795 2.0831 2.0533
Columns 8 through 11
2.0641 2.2612 2.7836 3.6708
>> Y_min=Y-DELTA;
>> Y_max=Y+DELTA;
>> f=p(1)*X.^2+ p(2).* X + p(3);
>> plot(X,Y,'+', X, Y_min,X,Y_max,x,y,'o',X,f)
>> grid on
Расчет значений квадратической модели и их 95%
доверительных интервалов для матрицы значений Х.
>> x=1:1:10;
>> d=normrnd(0,2,1,10);
>> y=x.^2/5+d;
>> [p S] = polyfit(x,y,2)
p =
0.2601 -0.6233 1.1314
S =
R: [3x3 double]
df: 7
normr: 4.1858
>> X = magic(3)
X =
8 1 6
3 5 7
4 9 2
>> [Y DELTA] = polyval(p,X,S)
Y =
12.7887 0.7682 6.7537
1.6021 4.5164 9.5112
2.7992 16.5863 0.9251
DELTA =
1.7210 2.0126 1.7505
1.7210 1.7505 1.7298
1.7298 1.7891 1.7891
regress - Множественная линейная регрессия
Синтаксис
b = regress(y,X)
[b,bint,r,rint,stats] = regress(y,X)
[b,bint,r,rint,stats] = regress(y,X,alpha)
Описание
b = regress(y,X) функция предназначена для расчета точечных оценок коэффициентов линейного уравнения регрессии b. Расчет точечных оценок коэффициентов выполняется методом наименьших квадратов из следующего уравнения линейной модели:
![]() ,
,
где ![]() - вектор значений зависимой переменной;
- вектор значений зависимой переменной; ![]() - вектор коэффициентов линейной модели;
- вектор коэффициентов линейной модели; ![]() - матрица значений независимых переменных;
- матрица значений независимых переменных; ![]() - вектор случайных возмущающих факторов, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией
- вектор случайных возмущающих факторов, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией ![]() ,
, ![]() .
.
Размерности векторов значений зависимой переменной ![]() и случайных возмущающих факторов
и случайных возмущающих факторов ![]() - n×1, где n - количество наблюдений. Размерность матрицы Х равна n×p, где p - количество независимых переменных. Столбцы матрицы Х соответствуют независимым переменных, строки - наблюдениям. Размерность вектора коэффициентов линейной регрессионной модели равна p×1. Коэффициенты множественной линейной регрессионной модели в векторе b располагаются по возрастанию степени независимых переменных.
- n×1, где n - количество наблюдений. Размерность матрицы Х равна n×p, где p - количество независимых переменных. Столбцы матрицы Х соответствуют независимым переменных, строки - наблюдениям. Размерность вектора коэффициентов линейной регрессионной модели равна p×1. Коэффициенты множественной линейной регрессионной модели в векторе b располагаются по возрастанию степени независимых переменных.
[b,bint,r,rint,stats] = regress(y,X) функция возвращает: b - вектор точечных оценок коэффициентов линейного уравнения регрессии, bint - матрицу интервальных оценок параметров линейной регрессии, r - вектор остатков, rint - матрицу 95% доверительных интервалов остатков, stats - структуру, содержащую значения статистики ![]() с соответствующими ей F статистикой и уровнем значимости p для регрессионной модели.
с соответствующими ей F статистикой и уровнем значимости p для регрессионной модели.
Размерность матрицы bint составляет p×2, где первый столбец матрицы задает нижнюю границу 95% доверительного интервала, второй - верхнюю границу 95% доверительного интервала. Количество элементов вектора r равно n. Размерность матрицы rint равна n×2, где первый и второй столбцы используются для задания нижней и верхней границ 95% доверительного интервала по каждому из n наблюдений.
[b,bint,r,rint,stats] = regress(y,X,alpha) входной параметр alpha позволяет задать величину уровня значимости. Уровень значимости используется для расчета границ доверительных интервалов bint и rint с доверительной вероятностью определяемой как 100(1-alpha)%. Значение alpha=0.2 будет соответствовать 80% границам доверительных интервалов bint и rint.
Примеры использования функции расчета значений параметров множественной линейной регрессионной модели
1. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() .
.
1.1. Моделирование матрицы значений независимой переменной
>> X = [ones(10,1) (1:10)']
X =
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
1.2. Моделирование вектора значений зависимой переменной
>> y = X * [10;1] + normrnd(0,0.1,10,1)
y =
10.9606
12.0310
13.0405
14.1457
14.9772
15.9760
16.8907
17.9328
18.9891
20.1052
1.3. Расчет параметров линейной регрессионной модели и их 95% границ доверительных интервалов
>> [b,bint] = regress(y,X,0.05)
b =
10.0148
0.9982
bint =
9.8858 10.1437
0.9774 1.0190
1.4. Графическое представление выборочных данных, регрессионной модели и прямых регрессионной модели для границ параметров доверительных интервалов
>> Xx = 1:1:10;
>> Yy = b(1)+ b(2).*Xx;
>> Yn = bint(1,1)+ bint(2,1).*Xx;
>> Yv = bint(1,2)+ bint(2,2).*Xx;
>> plot(Xx,Yy,'r', Xx,Yn,'g--', Xx,Yv,'g--',X(:,2),y,'bo')
>> grid on
.jpg)
1.5. Расчет параметров линейной регрессионной модели, их 99% границ доверительных интервалов, вектора значений остатков, их 99% границ доверительных интервалов и структуру stats.
>> [b,bint,r,rint,stats] = regress(y,X,0.01)
b =
9.9866
1.0009
bint =
9.7307 10.2425
0.9597 1.0422
r =
-0.0146
0.0062
-0.0428
-0.1812
0.1223
0.1824
0.0706
0.0043
-0.0927
-0.0544
rint =
-0.3380 0.3089
-0.3409 0.3532
-0.4023 0.3167
-0.4764 0.1140
-0.2237 0.4684
-0.1182 0.4829
-0.2927 0.4338
-0.3592 0.3678
-0.4194 0.2339
-0.3710 0.2621
stats =
1.0e+003 *
0.0010 6.6321 0.0000
1.6. Графическое представление выборочных данных, регрессионной модели и прямых регрессионной модели для границ параметров доверительных интервалов
>> Xx = 1:1:10;
>> Yy = b(1)+ b(2).*Xx;
>> Yn = bint(1,1)+ bint(2,1).*Xx;
>> Yv = bint(1,2)+ bint(2,2).*Xx;
>> plot(Xx,Yy,'r', Xx,Yn,'g--', Xx,Yv,'g--',X(:,2),y,'bo')
>> grid on
.jpg)
1.7. Графическое представление вектора остатков и их границ доверительных интервалов
>> plot(X(:,2),r,'bo', X(:,2),rint(:,1),'g+', X(:,2),rint(:,2),'g+')
>> grid on
2. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(10,10,1);
>> X2 = unidrnd(20,10,1);
>> X=[ones(10,1) X1 X2]
X =
1 7 2
1 8 8
1 10 17
1 8 1
1 2 3
1 5 5
1 10 4
1 10 13
1 5 6
1 9 4
2.2. Моделирование вектора значений зависимой переменной
>> y = X * [1.5;2.5; 1.2] + normrnd(0,0.1,10,1)
y =
21.5191
31.2189
46.8962
22.7327
10.1175
19.9813
31.3726
42.0412
21.4183
28.7864
2.3. Расчет параметров линейной регрессионной модели, их 99% границ доверительных интервалов, вектора значений остатков, их 99% границ доверительных интервалов и структуру stats.
>> [b,bint,r,rint,stats] = regress(y,X,0.01)
b =
1.6080
2.4952
1.1962
bint =
1.3020 1.9140
2.4510 2.5393
1.1730 1.2195
r =
0.0525
0.0798
0.0008
-0.0328
-0.0695
-0.0836
0.0280
-0.0693
0.1572
-0.0630
rint =
-0.2436 0.3486
-0.2183 0.3780
-0.2153 0.2170
-0.3141 0.2484
-0.2699 0.1309
-0.3637 0.1965
-0.2484 0.3045
-0.3326 0.1939
-0.0444 0.3588
-0.3495 0.2234
stats =
1.0e+004 *
0.0001 6.6655 0.0000
2.4. Графическое представление выборочных данных, регрессионной модели и регрессионной модели для границ параметров доверительных интервалов
>> [Xx1 Xx2] = meshgrid([1:1:10],[1:2:20]);
>> Yy = b(1)+ b(2).*Xx1+ b(3).*Xx2;
>> Yn = bint(1,1)+ bint(2,1).*Xx1+ bint(3,1).*Xx2;
>> Yv = bint(1,2)+ bint(2,2).*Xx1+ bint(3,2).*Xx2;
>> mesh(Xx1, Xx2, Yy)
>> hold on
>> plot3(X1,X2,y,'o')
>> hold off
.jpg)
>> mesh(Xx1, Xx2, Yn)
>> hold on
>> plot3(X1,X2,y,'o')
>> hold off
.jpg)
>> mesh(Xx1, Xx2, Yv)
>> hold on
>> plot3(X1,X2,y,'o')
>> hold off
.jpg)
2.5. Графическое представление вектора остатков и их границ доверительных интервалов
>> plot(1:1:10,r,'bo', 1:1:10,rint(:,1),'g+', 1:1:10,rint(:,2),'g+')
>> grid on
regstats - Функция диагностирования линейной множественной модели. Графический интерфейс.
Синтаксис
regstats(responses,DATA,'model')
stats = regstats(responses,DATA,'model','whichstats')
Описание
regstats(responses, DATA,'model') функция предназначена для расчета параметров множественной регрессионной модели для вектора значений зависимой переменной responses, матрицы независимых переменных DATA, регрессионной модели 'model'. Функция отображает графическое окно с набором статистик, служащих для оценки качества множественной регрессионной модели (рис. 1). Для выбора статистик необходимо отметить соответствующие флажки. Диалоговое окно для редактирования идентификаторов переменных вызывается кнопкой "Calculate Now" (рис. 2). Выбранные статистики с заданными идентификаторами переменных будут рассчитаны и экспортированы в среду MATLAB после нажатия кнопки "ОК" (рис. 2).
.jpg)
Рис. 1. Графическое окно выбора статистик множественной регрессионной модели
.jpg)
Рис. 2. Графическое окно идентификаторов статистик множественной регрессионной модели в среде MATLAB.
Предусмотрены следующие виды регрессионных моделей:
|
Значение 'model' |
Состав эффектов множественной регрессионной модели |
|
'linear' |
Линейная модель, включающая линейные эффекты факторов и постоянный член. Принимается по умолчанию. |
|
'interaction' |
Линейная модель, включающая линейные эффекты и эффекты взаимодействия факторов, постоянный член. |
|
'quadratic' |
Квадратическая модель, включающая квадратические эффекты и эффекты взаимодействия факторов. |
|
'purequadratic' |
Квадратическая модель, включающая квадратические и линейные эффекты факторов, постоянный член. |
Последовательность коэффициентов множественной регрессионной модели соответствует их порядку, используемому в функции x2fx (см. описание x2fx).
Статистики множественной регрессионной модели приведенные на рис. 1 описаны в табл. 1. Последовательность статистик на рис. 1, 2 и в табл. 1 совпоадает.
stats = regstats(responses,DATA,'model','whichstats') функция возвращает структуру stats, содержащую статистики множественной регрессионной модели. Состав полей структуры stats определяет входной аргумент 'whichstats'. 'whichstats' может быть задан как строковая константа, например 'leverage', или массив ячеек содержащий строковые константы, например {'leverage' 'standres' 'studres'}. Допустимые строковые константы при формировании 'whichstats' приведены в табл .1.
Таблица 1.
|
Значение строковой константы |
Возвращаемая статистика |
|
'Q' |
Матрица Q при QR разложения матрицы независимых переменных DATA |
|
'R' |
Матрица R при QR разложения матрицы независимых переменных DATA |
|
'beta' |
Вектор точечных оценок коэффициентов регрессионной модели |
|
'covb' |
Ковариационная матрица коэффициентов регрессионной модели |
|
'yhat' |
Вектор зависимой переменной, рассчитанный по полученной регрессионной модели для исходных значений независимых переменных DATA |
|
'r' |
Вектор остатков |
|
'mse' |
Средняя квадратическая ошибка |
|
'leverage' |
Вектор степеней влияния отдельных наблюдений на коэффициенты регрессионной модели |
|
'hatmat' |
Матрица, проецирующая вектор наблюдений зависимой переменной на вектор наблюдений зависимой переменной, рассчитанной по регрессионной модели. |
|
's2_i' |
Вектор средних квадратических ошибок зависимой переменой, полученных без учета текущего наблюдения. |
|
'beta_i' |
Матрица коэффициентов регрессионной модели. Столбцы матрицы - векторы коэффициентов регрессионной модели, полученные последовательно без учета одного из наблюдений. |
|
'standres' |
Вектор стандартизованных остатков (остатков деленных на величину их среднего квадратического отклонения) |
|
'studres' |
Вектор стандартизованных остатков без учета текущего наблюдения (остатков деленных на величину соответствующего элемента вектора 's2_i') |
|
'dfbetas' |
Матрица влияния коэффициентов регрессионной модели. Столбцы матрицы - векторы коэффициентов регрессионной модели не содержащие соответствующего коэффициента, полученные последовательно без учета одного из наблюдений. |
|
'dffit' |
Вектор поправок к значениям зависимой переменной, рассчитанных без учета текущего наблюдения. |
|
'dffits' |
Вектор поправок к значениям зависимой переменной, рассчитанных без учета текущего наблюдения - 'dffit', нормированный на величину стандартной ошибки. |
|
'covratio' |
Вектор отношений обобщенной дисперсии при определении значений коэффициентов регрессионной модели без текущего наблюдения к обобщенной дисперсии коэффициентов регрессии с учетом всех наблюдений. |
|
'cookd' |
Вектор расстояний Кука. Элементы вектора расстояний Кука находятся как нормализованная поправка к вектору коэффициентов без учета текущего наблюдения. |
|
'all' |
Создание структуры stats, включающей все перечисленные выше статистики. |
Для получения более детальной информации по каждой статистике используется кнопка Help в окне выбора рассчитываемых статистик множественной регрессионной модели (рис.1).
Алгоритм расчета коэффициентов уравнения регрессии
Расчет точечных оценок коэффициентов выполняется методом наименьших квадратов из следующего уравнения линейной модели:
![]() ,
,
где ![]() - вектор значений зависимой переменной;
- вектор значений зависимой переменной; ![]() - вектор коэффициентов линейной модели;
- вектор коэффициентов линейной модели; ![]() - матрица значений независимых переменных;
- матрица значений независимых переменных; ![]() - вектор случайных возмущающих факторов, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией
- вектор случайных возмущающих факторов, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией ![]() ,
, ![]() .
.
Размерности векторов значений зависимой переменной ![]() и случайных возмущающих факторов
и случайных возмущающих факторов ![]() - n×1, где n - количество наблюдений. Размерность матрицы Х равна n×p, где p - количество независимых переменных. Столбцы матрицы Х соответствуют независимым переменных, строки - наблюдениям. Размерность вектора коэффициентов линейной регрессионной модели составит p×1.
- n×1, где n - количество наблюдений. Размерность матрицы Х равна n×p, где p - количество независимых переменных. Столбцы матрицы Х соответствуют независимым переменных, строки - наблюдениям. Размерность вектора коэффициентов линейной регрессионной модели составит p×1.
При расчете коэффициентов используется QR разложение матрицы наблюдений независимых переменных X=Q*R, где Q - прямоугольная матрица, R - треугольная матрица. Матрицы Q и R используются при расчете статистик приведенных в табл. 1.
Основным приводимым в литературе алгоритмом решения приведенного уравнения методом наименьших квадратов является:
![]() .
.
Однако такой способ решения имеет некоторые существенные недостатки. В частности не всегда возможно найти значение ![]() в силу конечной точности вычислений. Более стабильным численным решением считается
в силу конечной точности вычислений. Более стабильным численным решением считается
b = R\(Q'*y).
Этот алгоритм расчета точечных оценок множественной регрессионной модели используется в функции regstats.
Примеры использования функции расчета параметров и диагностики множественной регрессионной модели
1. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(10,10,1);
>> X2 = unidrnd(20,10,1);
>> X=[X1 X2]
X =
10 13
3 16
7 19
5 15
9 4
8 9
5 19
1 19
9 9
5 18
1.2. Моделирование вектора значений зависимой переменной
>> y = X * [2.5; 1.2] + normrnd(0,0.1,10,1)
y =
40.5567
26.5334
40.3125
30.5288
27.1854
30.9191
35.4189
25.2962
33.3327
34.1175
1.3. Расчет параметров и диагностика линейной множественной регрессионной модели
>> regstats(y,X, 'linear')
Выбираются следующие статистики:
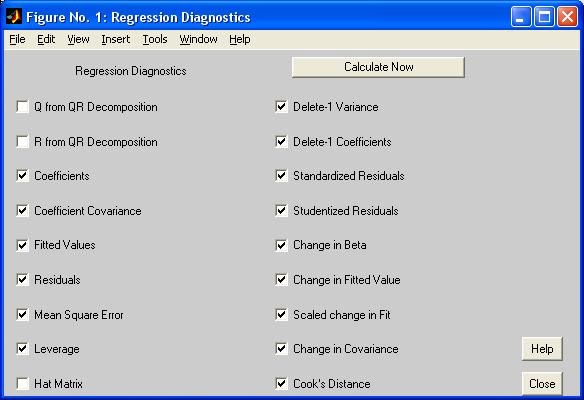
Идентификаторы переменных для экспорта в среду MATLAB принмаются в соотвествии со следующим диалогом:
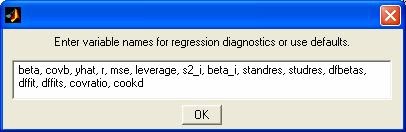
Результаты расчета и экспорта
>> beta
beta =
-0.1992
2.5130
1.2084
>> beta_i
beta_i =
Columns 1 through 8
-0.3169 -0.0580 -0.2617 -0.2119 -0.0530 -0.2760 -0.1536 -0.2345
2.5251 2.5008 2.5174 2.5139 2.5089 2.5138 2.5109 2.5167
1.2124 1.2052 1.2114 1.2086 1.2009 1.2123 1.2053 1.2090
Columns 9 through 10
-0.2063 -0.1991
2.5120 2.5130
1.2090 1.2084
>> covb
covb =
0.0401 -0.0027 -0.0016
-0.0027 0.0002 0.0001
-0.0016 0.0001 0.0001
>> yhat
yhat =
40.6404
26.6744
40.3517
30.4921
27.2517
30.7807
35.3257
25.2736
33.2938
34.1173
>> r
r =
-0.0837
-0.1410
-0.0392
0.0367
-0.0664
0.1384
0.0932
0.0227
0.0390
0.0002
2. Рассматривается полная квадратическая регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(10,10,1);
>> X2 = unidrnd(20,10,1);
>> X=[X1.^2 X2.^2 X1 X2 X1.*X2]
X =
1 1 1 1 1
16 225 4 15 60
81 81 9 9 81
1 361 1 19 19
4 100 2 10 20
9 81 3 9 27
4 289 2 17 34
49 121 7 11 77
9 25 3 5 15
4 196 2 14 28
2.2. Моделирование вектора значений зависимой переменной
>> y = X * [1.2; 2.5; 1.5; -1.3; -0.89] + normrnd(0,0.1,10,1)
y =
2.9913
514.8726
229.3512
863.8083
226.9864
182.0814
678.0467
288.9759
57.9404
454.5968
2.3. Расчет параметров и диагностика квадратической регрессионной модели
>> regstats(y, [X1 X2], 'quadratic')
Выбираются следующие статистики:
.jpg)
Идентификаторы переменных для экспорта в среду MATLAB принмаются в соотвествии со следующим диалогом:
.jpg)
Результаты расчета и экспорта:
>> beta
beta =
-0.0865
1.6113
-1.3351
-0.8937
1.1931
2.5025
>> beta_i
beta_i =
Columns 1 through 8
-0.0175 -0.0873 -0.0800 -0.0648 -0.1287 -0.0685 -0.0863 -0.0853
1.5897 1.6108 1.6011 1.5810 1.6760 1.5996 1.6114 1.6092
-1.3415 -1.3340 -1.3323 -1.3280 -1.3591 -1.3392 -1.3353 -1.3337
-0.8926 -0.8939 -0.8941 -0.8908 -0.8949 -0.8930 -0.8936 -0.8939
1.1941 1.1934 1.1952 1.1932 1.1890 1.1939 1.1931 1.1934
2.5027 2.5025 2.5024 2.5017 2.5038 2.5027 2.5025 2.5025
Columns 9 through 10
-0.2207 -0.0534
1.7811 1.5521
-1.3498 -1.3154
-0.9008 -0.8922
1.1835 1.1966
2.5036 2.5015
>> r
r =
-0.0004
0.0041
-0.0082
0.0296
0.0503
0.0367
-0.0073
0.0138
-0.0278
-0.0908
>> mse
mse =
0.0035
>> s2_i
s2_i =
0.0047
0.0047
0.0045
0.0034
0.0028
0.0040
0.0047
0.0046
0.0032
0.0006
3. Рассматривается не полная квадратическая регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , - параметры линейной регрессионной модели,
, - параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
3.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(10,10,1);
>> X2 = unidrnd(20,10,1);
>> X=[X1.^2 X2.^2 X1 X2 ]
X =
1 1 1 1 1
16 225 4 15 60
81 81 9 9 81
1 361 1 19 19
4 100 2 10 20
9 81 3 9 27
4 289 2 17 34
49 121 7 11 77
9 25 3 5 15
4 196 2 14 28
3.2. Моделирование вектора значений зависимой переменной
>> y = X * [1.2; 2.5; 1.5; -1.3] + normrnd(0,0.1,10,1)
y =
2.9913
514.8726
229.3512
863.8083
226.9864
182.0814
678.0467
288.9759
57.9404
454.5968
3.3. Расчет параметров и диагностика не полной квадратической регрессионной модели. В качестве дополнительного вхоного аргумента задается спецификатор выходной структуры stats - 'whichstats'.
>> whichstats={'beta', 'covb', 'yhat', 'r', 'mse', 'beta_i'};
>> stats=regstats(y, [X1 X2], 'purequadratic', whichstats)
stats =
source: 'regstats'
beta: [5x1 double]
covb: [5x5 double]
yhat: [10x1 double]
r: [10x1 double]
mse: 0.0025
beta_i: [5x10 double]
>> stats.beta
ans =
-0.4396
1.5932
-1.2257
1.1918
2.4960
>> stats.covb
ans =
0.0475 0.0025 -0.0068 -0.0005 0.0002
0.0025 0.0013 -0.0006 -0.0001 0.0000
-0.0068 -0.0006 0.0011 0.0001 -0.0000
-0.0005 -0.0001 0.0001 0.0000 -0.0000
0.0002 0.0000 -0.0000 -0.0000 0.0000
>> stats.yhat
ans =
145.4677
474.3992
182.8344
313.5338
145.4677
524.0781
238.5186
823.9587
811.6394
352.2278
>> stats.r
ans =
0.0618
-0.0328
-0.0629
0.0286
-0.0369
0.0077
0.0068
-0.0181
0.0165
0.0293
>> stats.mse
ans =
0.0025
>> stats.beta_i
ans =
Columns 1 through 8
-0.5617 -0.4273 -0.3386 -0.4948 -0.3668 -0.4018 -0.3981 -0.4405
1.6022 1.5337 1.6289 1.5739 1.5879 1.5935 1.5960 1.5957
-1.2089 -1.2086 -1.2417 -1.2188 -1.2357 -1.2310 -1.2322 -1.2283
1.1910 1.1976 1.1875 1.1944 1.1923 1.1915 1.1912 1.1916
2.4954 2.4955 2.4963 2.4959 2.4964 2.4962 2.4962 2.4962
Columns 9 through 10
-0.4694 -0.4877
1.5900 1.5947
-1.2195 -1.2233
1.1923 1.1921
2.4957 2.4960
ridge - Линейная регрессия с применением гребневых оценок (ридж-регрессия)
Синтаксис
b = ridge(y,X,k)
Описание
b = ridge(y,X,k) функция предназначена для расчета гребневых оценок параметров линейной регрессионной модели:
![]() ,
,
где ![]() - вектор значений зависимой переменной;
- вектор значений зависимой переменной; ![]() - вектор коэффициентов линейной модели;
- вектор коэффициентов линейной модели; ![]() - матрица значений независимых переменных;
- матрица значений независимых переменных; ![]() - вектор случайных возмущающих факторов, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией
- вектор случайных возмущающих факторов, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией ![]() ,
, ![]() .
.
Размерности векторов значений зависимой переменной ![]() и случайных возмущающих факторов
и случайных возмущающих факторов ![]() - n×1, где n - количество наблюдений. Размерность матрицы Х равна n×p, где p - количество независимых переменных. Столбцы матрицы Х соответствуют независимым переменных, строки - наблюдениям. Размерность вектора коэффициентов линейной регрессионной модели составит p×1.
- n×1, где n - количество наблюдений. Размерность матрицы Х равна n×p, где p - количество независимых переменных. Столбцы матрицы Х соответствуют независимым переменных, строки - наблюдениям. Размерность вектора коэффициентов линейной регрессионной модели составит p×1.
Гребневые оценки параметров линейной регрессионной модели ![]() рассчитываются из следующего выражения:
рассчитываются из следующего выражения:
![]() ,
,
где ![]() - параметр ридж-регрессии, задается как скалярная величина.
- параметр ридж-регрессии, задается как скалярная величина.
При ![]() гребневые оценки параметров линейной регрессионной модели b совпадают с точечными оценками, полученными методом наименьших квадратов. Если величина
гребневые оценки параметров линейной регрессионной модели b совпадают с точечными оценками, полученными методом наименьших квадратов. Если величина ![]() увеличивается, то постоянное смещение коэффициентов b увеличивается, а дисперсия оценки уменьшается. Для матрицы независимых переменных Х с низким числом обусловленности уменьшение величины дисперсии оценок коэффициентов происходит быстрее, чем компенсируется величина постоянного смещения.
увеличивается, то постоянное смещение коэффициентов b увеличивается, а дисперсия оценки уменьшается. Для матрицы независимых переменных Х с низким числом обусловленности уменьшение величины дисперсии оценок коэффициентов происходит быстрее, чем компенсируется величина постоянного смещения.
Примеры использования функции расчета гребневых оценок параметров линейной регрессионной модели
1. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Моделирование вектора значений независимой переменной
>> X1 = unidrnd(10,10,1);
1.2. Моделирование вектора значений зависимой переменной
>> X=[X1 ones(10,1)]
X =
7 1
8 1
10 1
8 1
2 1
5 1
10 1
10 1
5 1
9 1
>> y = X * [1.2; 2.5] + normrnd(0,0.1,10,1)
y =
10.8813
12.1726
14.4412
12.3183
4.8864
8.5114
14.6067
14.5059
8.4904
13.2168
1.3. Расчет гребневых оценок параметров линейной регрессионной модели для коэффициента Ридж-регрессии равного k=[0:0.5:1]
>> k=[0:0.5:1];
>> b1 = ridge(y,X1,k(1))
b1 =
3.3861
>> b2 = ridge(y,X1,k(2))
b2 =
3.2079
>> b3 = ridge(y,X1,k(3))
b3 =
3.0475
2. Зависимость изменения параметров линейной регрессионной модели от величины коэффициента Ридж-регрессии. График строится для каджого из 4-х коэффициентов при независимых переменных, ingredients, в регрессионной модели.
>> load hald;
>> b = zeros(4,100);
>> kvec = 0.01:0.01:1;
>> count = 0;
>> for k = 0.01:0.01:1 count = count + 1; b(:,count) = ridge(heat,ingredients,k); end
>> plot(kvec',b'),xlabel('k'),ylabel('b','FontName','Symbol')
>> grid on
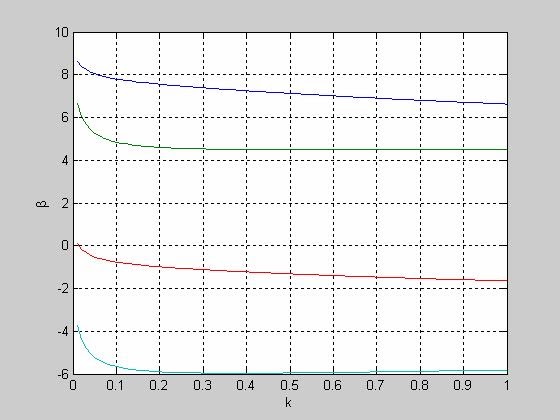
rstool - Интерактивный подбор и визуализация поверхности отклика
Синтаксис
rstool(x,y)
rstool(x,y,'model')
rstool(x,y,'model',alpha,'xname','yname')
Описание
rstool(x,y) функция предназначена для расчета параметров и построения графика множественной линейной регрессионной модели для матрицы независимых переменных х и вектора значений зависимой переменной y. На графике регрессионной модели отображаются границы 95% доверительного интервала регрессионной модели. Результаты проведенных расчетов отображаются в графическом окне (рис. 1). Зеленая линия соответствует рассчитанной по регрессионной модели зависимой переменной, красные пунктирные линии - границам доверительного интервала. По столбцам матрицы х задаются значения наблюдений независимых переменных. Строки х соответствуют наблюдениям. Количество строк х и элементов вектора y должно быть равно.
.jpg)
Рис. 1. Графическое окно интерактивного расчета и представления результатов множественной регрессии
Изменяя мышью положение синей пунктирной линии в окнах графиков переменных Х1, Х2, Х3 (рис. 1) или вводя значения независимых переменных в строки ввода под графиками можно рассчитать новые точечные и интервальные оценки зависимой переменной в интерактивном режиме. Результаты расчет будут отображаться в левой части графического окна "Predicted Y1" и автоматически пересчитываться после изменения значения хотя бы одной переменной.
Меню Export (рис. 2) предназначено для экспорта в среду MATLAB: вектора параметров регрессионной модели - Parameters, корня квадратного из средней квадратической ошибки - RMSE, вектора остатков - Residuals, всех перечисленных выше параметров - All.
.jpg)
Рис. 2. Меню Export.
После выбора пункта меню Export будет предложено изменить идентификатор соответствующей переменной в среде MATLAB. При выборе пункта "All" диалог изменения идентификаторов и экспорта переменных в рабочую область MATLAB примет вид (рис. 3)
.jpg)
Рис. 3. Диалог изменения идентификаторов и экспорта переменных при выборе пункта "All" меню Export.
Нажатие кнопки "OK" приведет к экспорту переменных. Аналогичные диалоговые окна будет соответствовать пунктам "RMSE", "Residuals", "Parameters".
В следующем за Export меню можно выбрать вид регрессионной модели (рис. 4). После изменения вида модели будут пересчитаны коэффициенты регрессионной модели и параметры RMSE, Residuals. Автоматически будет перестроены графики регрессионной модели и границ ее доверительных интервалов.
.jpg)
Рис. 4. Меню выбора вида регрессионной модели.
Предусмотрены следующие виды регрессионных моделей:
Таблица 1.
|
Значение 'model' |
Состав эффектов множественной регрессионной модели |
|
'linear' |
Линейная модель, включающая линейные эффекты факторов и постоянный член. Принимается по умолчанию. |
|
'interaction' |
Линейная модель, включающая линейные эффекты и эффекты взаимодействия факторов, постоянный член. |
|
'quadratic' |
Квадратическая модель, включающая квадратические эффекты и эффекты взаимодействия факторов. |
|
'purequadratic' |
Квадратическая модель, включающая квадратические и линейные эффекты факторов, постоянный член. |
|
'User Specified' |
Модель первоначально определенная пользователем при помощи входного параметра 'model'. |
Кнопка Close позволяет закрыть графическое окно интерактивной множественной регрессии (рис. 1).
rstool(x,y,'model') входной параметр 'model' позволяет пользователю задать вид начальной регрессионной модели отображаемой в графическом окне множественной регрессии (рис. 1). Параметр 'model' может принимать следующие значения: 'interaction', 'quadratic', 'purequadratic'. По умолчанию 'model'='linear'. Описание регрессионных моделей приведено в табл. 1.
rstool(x,y,'model',alpha) входной параметр alpha позволяет задать уровень значимости. Доверительная вероятность для границ доверительного интервала определяется как 100(1-alpha)%. Например, при alpha=0.01 доверительная вероятность будет равна 99%.
Если в качестве y задать матрицу, то каждый ее столбец будет трактоваться как отдельная зависимая переменная от всех независимых переменных х (столбцов матрицы х). Задача множественной регрессии будет решаться поочередно сначала для первой зависимой переменной (первого столбца y), затем второй зависимой переменной и т.д. Графическое представление такой задачи будет иметь вид матрицы графиков (рис. 5), где "Predicted Y1" является первым столбцом матрицы y, "Predicted Y2" - вторым столбцом y и т.д. Все графики будут построены в одинаковом масштабе для независимых переменных х. Изменение значения одной из независимых переменных мышью в окне графика или вводом ее значения в соответствующую строку ввода приведет автоматическому пересчету точечных и интервальных оценок всех зависимых переменных. Векторы параметров регрессионных моделей Parameters и остатков Residuals при экспорте будут преобразованы в матрицы с числом столбцов равным количеству регрессионных моделей или зависимых переменных y. Первый столбец Parameters и Residuals будет соответствовать y(:,1) и т.д. Скаляр RMSE будет преобразован в вектор-строку с числом элементов равным size(y,2). При изменении вида регрессионной модели новая модель будет применена ко всем зависимостям, и указанным выше образом, будут пересчитаны экспортируемые параметры.
.jpg)
Рис. 5. Графическое окно интерактивного расчета и представления результатов множественной регрессии для 2 зависимых переменных.
rstool(x,y,'model',alpha,'xname','yname') входные параметры 'xname' и 'yname' позволяют задать метки на графиках для независимых и зависимы переменных. 'xname' задается как вектор строковых переменных. 'yname' определяется как строковая переменная.
Примеры использования функции расчета параметров и графического представления множественной регрессионной модели в интерактивном режиме
1. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(10,10,1);
>> X2 = unidrnd(20,10,1);
>> X=[X1 X2]
X =
2 10
7 18
4 17
6 13
2 17
7 14
4 7
9 6
9 7
6 11
1.2. Моделирование вектора значений зависимой переменной
>> y = X * [1.2; 2.5] + normrnd(0,2,10,1)
y =
28.6465
54.9981
49.1818
37.7158
45.3241
43.8758
20.2845
24.3159
30.4646
34.4370
1.3. Интерактивный множественный регрессионный анализ
>> rstool(X,y)
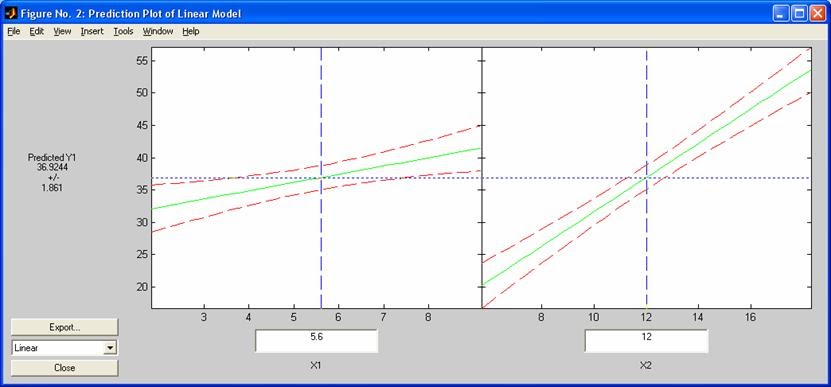
Экспорт параметров регрессионной модели в среду MATLAB
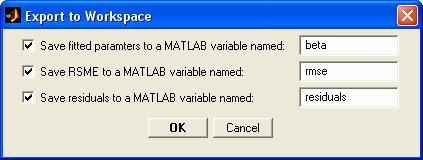
>> beta
beta =
-2.1124
1.2748
2.6581
>> rmse
rmse =
1.6296
>> residuals
residuals =
1.6277
0.3401
1.0064
-2.3767
-0.3017
-0.1497
-1.3095
-0.9940
2.4965
-0.3392
2. Рассматривается полная квадратическая регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(5,10,1);
>> X2 = unidrnd(7,10,1);
>> X=[X1.^2 X2.^2 X1 X2 X1.*X2]
X =
9 4 3 2 6
9 9 3 3 9
9 36 3 6 18
4 25 2 5 10
9 16 3 4 12
4 16 2 4 8
9 36 3 6 18
16 1 4 1 4
9 25 3 5 15
16 1 4 1 4
2.2. Моделирование вектора значений зависимой переменной
>> y = X * [1.2; 2.5; 1.5; -1.3; -0.89] + normrnd(0,2,10,1)
y =
17.6173
27.2029
79.1444
53.9788
38.8951
33.0537
78.8411
24.7024
57.9725
21.5497
2.3. Интерактивный множественный регрессионный анализ
>> rstool([X1 X2],y,'quadratic')
.jpg)
Экспорт параметров регрессионной модели в среду MATLAB
.jpg)
>> beta1
beta1 =
-70.1331
38.3488
8.4771
-3.4428
-3.5619
2.1482
>> rmse1
rmse1 =
1.2919
>> residuals1
residuals1 =
-0.1291
0.5671
0.0617
0.0000
-0.9266
0.0000
-0.2415
1.5764
0.6685
-1.5764
3. Рассматривается не полная квадратическая регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
3.1. Моделирование матрицы значений независимых переменных
>> X1 = unidrnd(5,10,1);
>> X2 = unidrnd(6,10,1);
>> X=[X1.^2 X2.^2 X1 X2 ]
X =
9 4 3 2
4 16 2 4
25 4 5 2
1 36 1 6
16 25 4 5
25 9 5 3
25 25 5 5
16 4 4 2
9 9 3 3
9 36 3 6
3.2. Моделирование вектора значений зависимой переменной
>> y = X * [1.2; 2.5; 1.5; -1.3] + normrnd(0,2,10,1)
y =
24.3115
43.0633
42.9205
87.5792
81.7790
59.0578
95.7761
31.2317
31.3161
97.3541
3.3. Интерактивный множественный регрессионный анализ. Границы доверительного интревала регрессионной модели расчитываются для доверительной вероятности 99%. Для независимых и зависимой переменных заданы метки.
>> alpha=0.01;
>> xnames=['Xx1'; 'Xx2'];
>> yname='Yy';
>> rstool([X1 X2],y, 'purequadratic', alpha,xnames,yname)
.jpg)
Изменение вида регрессионной модели: неполной квадратической на полную модель. Изменение выполняется при помощи соотвествующего меню.
.jpg)
Экспорт параметров регрессионной модели в среду MATLAB
.jpg)
>> beta2
beta2 =
1.6073
-1.7355
0.1445
1.7017
2.3633
>> rmse2
rmse2 =
2.0957
>> residuals2
residuals2 =
2.8531
-0.2701
-2.2945
0.0611
0.0820
1.8821
0.4991
-0.4032
-2.1030
-0.3067
robustfit - Робастная оценка параметров регрессионной модели
Синтаксис
b = robustfit(X,Y)
[b,stats] = robustfit(X,Y)
[b,stats] = robustfit(X,Y,'wfun',tune,'const')
Описание
b = robustfit(X,Y) функция позволяет получить робастные оценки параметров регрессионной модели b для матрицы независимых переменных Х и вектора значений зависимой переменной. Столбцы матрицы Х представляют отдельные независимые переменные, строки - наблюдения. Количество элементов вектора Y и строк матрицы Х должно совпадать. В robustfit реализуется итерационный взвешенный метод наименьших квадратов. Веса на текущей итерации вычисляются при помощи биквадратический функции от вектора остатков, рассчитанных на предыдущей итерации. Использование такого алгоритма позволяет задать меньшие значения весов для наблюдений, имеющих большее отклонение от регрессионной модели по отношению к остальным. Результаты расчета b менее чувствительны к случайным выбросам в выборке, чем при использовании метода наименьших квадратов.
[b,stats] = robustfit(X,Y) функция возвращает вектор точечных оценок коэффициентов регрессионной модели b и структуру stats, содержащую следующие поля:
stats.ols_s - корень квадратный из средней квадратической ошибки при расчете параметров регрессионной модели методом наименьших квадратов;
stats.robust_s - робастная оценка стандартной ошибки;
stats.mad_s - оценка стандартной ошибки на основе абсолютных отклонений остатков относительно их медианы. Эта оценка используется для нормирования вектора остатков в итеративной процедуре расчета коэффициентов регрессионной модели;
stats.s - окончательная оценка стандартной ошибки. stats.s превышает значение robust_s и рассчитывается как взвешенное среднее от ols_s и robust_s;
stats.se - стандартная ошибка точечных оценок коэффициентов регрессионной модели;
stats.t - отношение вектора коэффициентов регрессионной модели b к их стандартным ошибкам stats.se;
stats.p - уровень значимости для статистики stats.t;
stats.coeffcorr - оценка коэффициентов корреляции оценок коэффициентов регрессионной модели;
stats.w - вектор весов при проведении робастной регрессии;
stats.h - вектор степеней влияния наблюдений на параметры регрессионной модели;
stats.dfe - число степеней свободы стандартной ошибки;
stats.R - матрица R из QR разложения матрицы независимых переменных Х.
В процессе робастной регрессии рассчитывается ковариационная матрица коэффициентов уравнения регрессии V. Расчет V выполняется как V=inv(X'*X)*stats.s^2. Стандартные ошибки и коэффициенты корреляции параметров регрессионной модели являются производными от V.
[b,stats] = robustfit(X,Y,'wfun',tune,'const') дополнительные входные аргументы 'wfun', tune, 'const' позволяют задать функцию весов, согласующую постоянную и указать наличие или отсутствие постоянного члена соответственно. Предусмотрены следующие функции весов
Таблица 1
|
Весовая функция |
Вид весовой функции |
Согласующая постоянная |
|
'andrews' |
w = (abs(r)<pi) .* sin(r) ./ r |
1.339 |
|
'bisquare' |
w = (abs(r)<1) .* (1 - r.^2).^2 |
4.685 |
|
'cauchy' |
w = 1 ./ (1 + r.^2) |
2.385 |
|
'fair' |
w = 1 ./ (1 + abs(r)) |
1.400 |
|
'huber' |
w = 1 ./ max(1, abs(r)) |
1.345 |
|
'logistic' |
w = tanh(r) ./ r |
1.205 |
|
'talwar' |
w = 1 * (abs(r)<1) |
2.795 |
|
'welsch' |
w = exp(-(r.^2)) |
2.985 |
Значение величины r входящей в весовую функцию определяется из выражения
r=resid/(tune*s*sqrt(1-h)),
где resid - вектор остатков от предыдущей итерации, tune - согласующая постоянная, h - вектор степеней влияния наблюдений после расчета параметров уравнения регрессии методом наименьших квадратов, s - оценка стандартного отклонения погрешности коэффициента уравнения регрессии:
s = MAD/0.6745.
Величина MAD является медианой абсолютных отклонений остатков относительно их медианы. Постоянная 0,6745 предназначена для получения несмещенной оценки s для нормального распределения. Если в матрице независимых переменных Х задано p столбцов, включая постоянный член, наименьшее p-1 абсолютное отклонение исключается при расчете их медианы.
В дополнении к приведенному выше списку весовых функций, входной параметр 'wfun' может быть равным 'ols', что приведет к использованию обычного, не взвешенного, метода наименьших квадратов.
Входной параметр tune позволяет задать новое значение согласующей постоянной, отличной от приведенных в табл. 1. Уменьшение величины согласующей постоянной приведет к уменьшению веса больших по абсолютной величине остатков и наоборот. Значения согласующих постоянных по умолчанию, приведенных в табл. 1, позволяют получить оценки коэффициентов уравнения регрессии, которые примерно в 95% случаев также эффективны, как и оценки полученные методом наименьших квадратов, при условии, что зависимая переменная распределена по нормальному закону без выбросов.
Входной параметр 'const' позволяет добавить постоянный член в уравнение регрессии, при 'const'='on', и удалить его, если 'const'='off'. Значение по умолчанию 'const'='on'. Если необходимо получить оценку постоянного члена уравнения регрессии, то необходимо указать 'const'='on', а не использовать единичный столбец в матрице Х.
В качестве весовой функции может быть использована функция пользователя. Пользовательская весовая функция может быть задана как inline-функция или m-функция. В этом случае в качестве параметра 'wfun' передается указатель на функцию пользователя, например @myfun. Функция, определяемая пользователем как весовая, должна получить в качестве входного аргумента вектор нормированных остатков, пересчитать его в вектор весов и вернуть последний как выходной параметр.
Примеры использования функции робастной регрессии
1. Сравнение линейных регрессионных моеделй полученных методом наименьших квадратов и робастной регрессии. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ;
; ![]() - независимая переменная.
- независимая переменная.
1.1. Моделирование вектора значений независимой переменной
>> x = (1:10)';
1.2. Моделирование вектора значений зависимой переменной
>> y = 10 - 2*x + normrnd (0,1,10,1);
1.3. Добавление выброса в вектор значений зависимой переменной
>> y(10) = 0;
1.4. Расчет параметров линейной регрессии методом наименьших квадратов
>> [bls bls_i] = regress(y,[ones(10,1) x])
bls =
7.2481
-1.3208
bls_i =
2.9493 11.5470
-2.0136 -0.6280
1.5. Расчет параметров ![]() ,
, ![]() с помощью робастной линейной регрессии
с помощью робастной линейной регрессии
>> brob = robustfit(x,y)
brob =
9.1114
-1.8238
1.6. Графическе представление полученных регрессионных моделей и экспериментальных точек
>> scatter(x,y)
>> hold on
>> plot(x,bls(1)+bls(2)*x,'g:')
>> plot(x,bls_i(1,1)+bls_i(2,1)*x,'b:')
>> plot(x,bls_i(1,2)+bls_i(2,2)*x,'b:')
>> plot(x,brob(1)+brob(2)*x,'r-')
>> grid on
>> hold off
.jpg)
2. Сравнение линейных регрессионных моеделй полученных методом наименьших квадратов и робастной регрессии. Рассматривается линейная регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Моделирование матрицы значений независимых переменных
>> x1 = unidrnd(10,10,1);
>> x2 = unidrnd(15,10,1);
>> x = [x1 x2];
2.2. Моделирование вектора значений зависимой переменной
>> y = 1.5 - 2*x1 + 3*x2 + normrnd(0,1,10,1);
2.3. Добавление выброса в вектор значений зависимой переменной
>> y(10) = -1;
2.4. Расчет параметров линейной регрессии методом наименьших квадратов
>> [bls bls_i] = regress(y,[ones(10,1) x])
bls =
11.4084
-2.4480
2.0494
bls_i =
-47.2846 70.1014
-6.9295 2.0335
-1.2252 5.3239
2.5. Расчет параметров ![]() ,
, ![]() с помощью робастной линейной регрессии. В качестве дополнительного входного параметра задана функция весов 'andrews'. Функция возвращает вектор коэффициентов робастной регрессии и структуру stats дополнительных результатов расчета.
с помощью робастной линейной регрессии. В качестве дополнительного входного параметра задана функция весов 'andrews'. Функция возвращает вектор коэффициентов робастной регрессии и структуру stats дополнительных результатов расчета.
>> [brob,stats] = robustfit(x,y, 'andrews')
brob =
2.3609
-2.1040
3.0121
stats =
ols_s: 12.0462
robust_s: 0.9394
mad_s: 1.2615
s: 8.3187
resid: [10x1 double]
rstud: [10x1 double]
se: [3x1 double]
coeffcorr: [3x3 double]
t: [3x1 double]
p: [3x1 double]
w: [10x1 double]
R: [3x3 double]
dfe: 7
h: [10x1 double]
>> stats.resid
ans =
-0.1284
0.0318
-0.8904
1.6972
-0.0974
0.0005
0.5445
-0.8669
-0.1050
-35.0101
>> stats.coeffcorr
ans =
1.0000 -0.8846 -0.9256
-0.8846 1.0000 0.6824
-0.9256 0.6824 1.0000
>> stats.se
ans =
17.1408
1.3088
0.9563
2.6. Графическое представление полученных регрессионных моделей и экспериментальных точек
>> plot3(x1,x2,y,'o')
>> hold on
>> [Xx1 Xx2]=meshgrid([1:0.5:10],[ 1:0.5:15]);
>> z= bls(1) + bls(2).*Xx1 + bls(3).*Xx2;
>> surfc(Xx1,Xx2,z)
>> grid on
>> hold off
.jpg)
>> plot3(x1,x2,y,'o')
>> hold on
>> [Xx1 Xx2]=meshgrid([1:0.5:10],[ 1:0.5:15]);
>> z= brob(1) + brob(2).*Xx1 + brob(3).*Xx2;
>> surf(Xx1,Xx2,z)
>> grid on
>> hold off
.jpg)
3. Сравнение регрессионных моеделй полученных методом наименьших квадратов и робастной регрессии. Рассматривается регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
3.1. Моделирование матрицы значений независимых переменных
>> x1 = unidrnd(5,10,1);
>> x2 = unidrnd(8,10,1);
>> x = [x1.^2 x2.^2];
3.2. Моделирование вектора значений зависимой переменной
>> y = 0.5+ 0.2*x1 + 0.3*x2 + normrnd(0,0.5,10,1);
3.3. Добавление выброса в вектор значений зависимой переменной
>> y(10) = 0;
3.4. Расчет параметров регрессии методом наименьших квадратов
>> [bls bls_i] = regress(y,[ones(10,1) x])
bls =
0.6668
0.0579
0.0396
bls_i =
-0.8973 2.2309
-0.0443 0.1601
-0.0021 0.0813
3.5. Расчет параметров ![]() ,
, ![]() с помощью робастной линейной регрессии. В качестве дополнительного входного параметра задана функция весов 'fair'. Согласующая постоянная принята равной 1,5. Функция возвращает вектор коэффициентов робастной регрессии и структуру stats дополнительных результатов расчета.
с помощью робастной линейной регрессии. В качестве дополнительного входного параметра задана функция весов 'fair'. Согласующая постоянная принята равной 1,5. Функция возвращает вектор коэффициентов робастной регрессии и структуру stats дополнительных результатов расчета.
>> tune=1.5;
>> [brob,stats] = robustfit(x,y, 'fair', tune,'on')
brob =
0.7386
0.0506
0.0420
stats =
ols_s: 1.0284
robust_s: 1.0223
mad_s: 0.9911
s: 1.0252
resid: [10x1 double]
rstud: [10x1 double]
se: [3x1 double]
coeffcorr: [3x3 double]
t: [3x1 double]
p: [3x1 double]
w: [10x1 double]
R: [3x3 double]
dfe: 7
h: [10x1 double]
>> stats.resid
ans =
0.3160
-0.4220
0.3814
0.4329
0.0925
0.9156
0.5785
-0.5956
-0.3295
-2.3021
>> stats.coeffcorr
ans =
1.0000 -0.5399 -0.7888
-0.5399 1.0000 0.2292
-0.7888 0.2292 1.0000
>> stats.se
ans =
0.6594
0.0431
0.0176
3.6. Графическое представление полученных регрессионных моделей и экспериментальных точек
>> plot3(x1,x2,y,'o')
>> hold on
>> [Xx1 Xx2]=meshgrid([1:0.2:5],[ 1:0.2:8]);
>> z= bls(1) + bls(2).*Xx1.^2 + bls(3).*Xx2.^2;
>> surf(Xx1,Xx2,z)
>> grid on
>> hold off
.jpg)
>> plot3(x1,x2,y,'o')
>> hold on
>> [Xx1 Xx2]=meshgrid([1:0.2:5],[ 1:0.2:8]);
>> z= brob(1) + brob(2).*Xx1.^2 + brob(3).*Xx2.^2;
>> surf(Xx1,Xx2,z)
>> grid on
>> hold off
.jpg)
stepwise - Пошаговая регрессия (графический интерфейс пользователя)
Синтаксис
stepwise(X,y)
stepwise(X,y,inmodel)
stepwise(X,y,inmodel,alpha)
Описание
stepwise(X,y) функция позволяет получить в интерактивном режиме регрессионную модель для зависимой переменной y от независимых переменных – столбцов матрицы X. Зависимая перемнная y задается как вектор. Число элементов вектора y должно быть равно количеству строк в матрице Х. Функция отображает три графических окна для управления процессом пошаговой регрессии (рис. 1, 3, 4). Элементы управления в графических окнах предназначены для удаления и добавления факторов, а также отображения статитстик, характеризующих текущую регрессионную модель.
.jpg)
Рис. 1.
График значений коэффициентов регрессии и их 95% доверительных интервалов (рис. 1) позволяет включать или удалять факторы из регрессионной модели в интреактивном режиме. Значения коэффициентов регрессии и границ их доверительных интервалов, включенные в модель, отображаются зеленым цветом. Коэффициенты регрессии, исключенные из регрессисоной модели, выделяются красным цветом. Включение или исключение фактора из регрессионной модели выполняется щелчком левой кнопки мыши на соотвествующей линии графика. Границы доверительных интервалов коэффициентов регрессии, значимо отличающихся от нуля, отображаются сплошными линиями. Границы доверительных интервалов коэффициентов, статистически не значимо отличающихся от нуля, отображаются штриховыми линиями, пересекающими вертикальную нулевую линию. Значение коэффициента, не включенного в модель, рассчитывается из предположения о его включении в состав текущей регрессионной зависимости.
Кпопка Scale Inputs служит для нормализации центрированных значений элементов столбцов матрицы независимых переменных Х на величину их среднего квадратического отклонения.
Кнопка Close позволяет закрыть графические окна (рис. 1, 3, 4).
Меню Export (рис. 2) используется для экспорта результатов пошаговой регрессии на текущем шаге в рабочую область MATLAB.
.jpg) .
.
Рис. 2.
Назначение пунктов меню Export:
-
Parameters - экспорт вектора коэффициентов регрессии;
-
Confidence Intervals - экспорт матрицы значений границ доверительных интервалов коэффициентов регрессии;
-
Terms In - экспорт вектора номеров независимых переменных, включенных в регрессионную модель;
-
Terms Out - экспорт вектора номеров независимых переменных, исключенных из регрессионной модели;
-
All - экспорт всех указанных выше параметров.
После выбора какого либо пункта меню Export будет отображено диалоговое окно, предназначенное для изменения инетификаторов экспортируемых переменных заданных по умолчанию. При выборе пукнта All будут приведены следующие идентификаторы экспортируемых переменных:
.jpg)
После нажатия кнопки "OK" переменные с заданными идентификаторами будут экспортированы в среду MATLAB.
Таблица с параметрами пошаговой регрессии (рис. 3) содержит в числовой форме информацию, приведенную на графике значений коэффициентов (рис. 1). Таблица содержит следующие столбцы: Colomn# - номер столбца матрицы независимых переменных, Parameter - значение коэффициента регрессии, Lower Confedence Intervals, Upper Confedence Intervals - нижняя и верхняя границы доверительного интервала коэффициента регрессионной модели. Кроме таблицы с параметрами регрессионной модели в графическом окне (рис. 2) приведены: RMSE - корень квадратный из средней квадратической ошибки, R-square - коэффициент детерминации, показывающий какая часть общей дисперсии может быть объяснена регрессионной моделью, F - статистика Фишера соотвествующая регрессионной модели, Р - уровень значимости статистики F.
.jpg)
Рис. 3.
Строки таблицы параметров регрессии (рис. 3), выделенные зеленым цветом, соотвествуют факторам включенным в модель. Факторы выделенные красным цветом исключены из регрессионной модели. Для включения или исключения факторов из регрессионной модели используется таже техника, что и в графическом окне приведенном на рис. 1.
Кнопка Close позволяет закрыть графические окна (рис. 1, 3, 4).
В графическом окне решений (рис. 4) отображается зависимость значений кореней квадратных из средней квадратической ошибки регрессионных моделей и границ доверительных интервалов RMSE от номера шага. Каждое включение или удаление фактора в регрессионную модель в графических окнах рис. 1, 3, приведет к добавлению соотвествующего графика в окне рис. 4. Возврат к предыдущей модели выполняется щелчком левой кнопки мыши по соотвествующему значению RMSE в графическом окне решений (рис. 4). Соотвествующие выделенной RMSE параметры регрессионной модели отображаются в новых графических окнах, аналогичных приведенным на рис. 1, 3.
.jpg)
Рис. 4.
stepwise(X,y,inmodel) входной аргумент inmodel позволяет управлять начальным множеством факторов, включенным в регрессионную модель. Элементы вектора inmodel являются номерами факторов, т.е. номерами столбцов матрицы Х.
stepwise(X,y,inmodel,alpha) входной аргумент alpha задает уровень значимости для расчетаграниц доверительного интервала коэффициентов регрессионной модели. alpha служит для проверки гипотезы о статистической значимости каждого фактора в регрессионной модели. По умолчанию, ![]() , где p - количество столбцов матрицы Х. Это значение alpha соответствует 95% доверительной вероятности. Доверительный интервал рассчитывается для регрессионной модели по всему диапазону изменения значений независимых переменных (используется метод Бонферони).
, где p - количество столбцов матрицы Х. Это значение alpha соответствует 95% доверительной вероятности. Доверительный интервал рассчитывается для регрессионной модели по всему диапазону изменения значений независимых переменных (используется метод Бонферони).
Примеры использования функции интерактивной пошаговой регрессии
1. Рассматривается регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Моделирование матрицы значений независимых переменных
>> x1 = unidrnd(10,10,1);
>> x2 = unidrnd(15,10,1);
>> x3 = unidrnd(8,10,1);
>> x = [x1 x2 x3];
1.2. Моделирование вектора значений зависимой переменной
>> y = -0.2*x1 + 0.3*x2 - 0.5*x3 + normrnd(0,0.5,10,1);
1.3. Интерактивный пошаговый регрессионный анализ
>> stepwise(x,y)
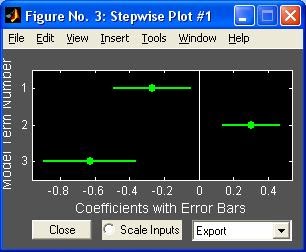
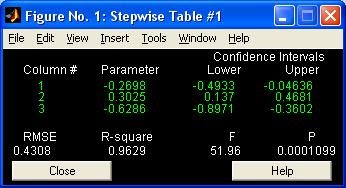
.jpg)
Как следует из приведенных выше графиков все коэффициенты значимы. При последовательном исключении каждого из факторов будет получен следующий график значений RMSE.
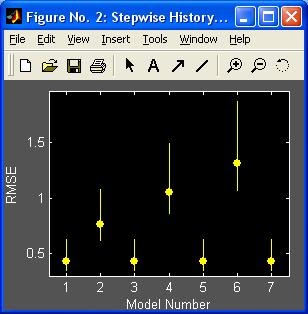
Т.е., регрессионная модель включающая все факторы будет обладать существенно меньшей погрешностью.
Экспорт параметров последней регрессионной модели:
.jpg)
>> beta
beta =
-0.2698
0.3025
-0.6286
>> betaci
betaci =
-0.4933 -0.0464
0.1370 0.4681
-0.8971 -0.3602
>> in
in =
1
2
3
>> out
out =
Empty matrix: 1-by-0
2. Рассматривается регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() , …,
, …, ![]() - независимые переменные.
- независимые переменные.
2.1. Моделирование матрицы значений независимых переменных
>> x1 = unidrnd(10,10,1);
>> x2 = unidrnd(15,10,1);
>> x3 = unidrnd(8,10,1);
>> x4 = normrnd(0,8,10,1);
>> x5 = weibrnd(1,2,10,1);
>> x = [x1 x2 x3 x4 x5];
2.2. Моделирование вектора значений зависимой переменной
>> y = -0.2*x1 + 0.3*x2 - 0.5*x3 + 0.01*x4 + 0.001*x5 + normrnd(0,0.5,10,1);
2.3. Интерактивный пошаговый регрессионный анализ
>> stepwise(x,y)
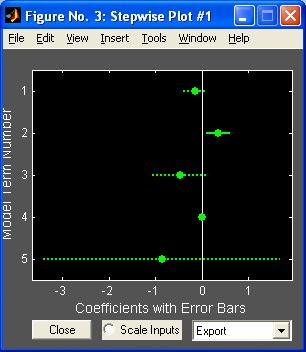
.jpg)
.jpg)
Исключая последовательно 4 и 5 факторы получим следующие параметры модели:
.jpg)
.jpg)
.jpg)
Последний результат можно получить используя команду
>> stepwise(X,y,[1 2 3])
3. Рассматривается регрессионная модель вида ![]() , где
, где ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры линейной регрессионной модели,
- параметры линейной регрессионной модели, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() , …,
, …, ![]() - независимые переменные.
- независимые переменные.
3.1. Моделирование матрицы значений независимых переменных
>> x1 = unidrnd(10,10,1);
>> x2 = unidrnd(15,10,1);
>> x3 = unidrnd(8,10,1);
>> x4 = normrnd(0,8,10,1);
>> x = [x1 x2 x3 x4];
3.2. Моделирование вектора значений зависимой переменной
>> y = -0.2*x1 + 0.3*x2 - 0.5*x3 + 0.01*x4 + normrnd(0,0.5,10,1);
3.3. Интерактивный пошаговый регрессионный анализ. При вызове функции stepwise исключается 3 фактор и границы доверительных интервалов рассчитываются для доверительной вероятности 99%.
>> alpha=0.01;
>> inmodel=[1 2 4];
>> stepwise(x,y,inmodel,alpha)
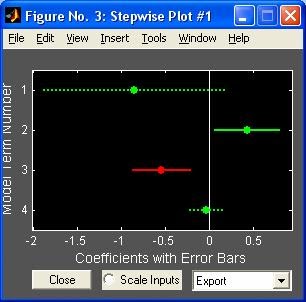
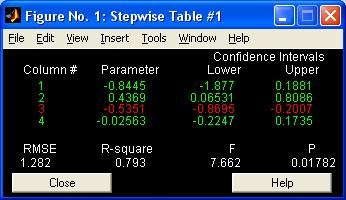
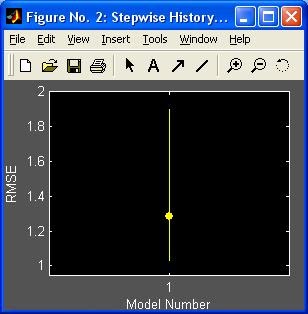
После включения 1, 2, 3 и исключения 4-го факторов будут получены следующие значения RMSE
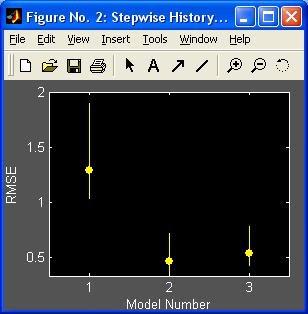
Как следует из приведенной выше графической зависимоси RMSE, включение 4-го фактора не приводит к существенному снижению погрешности модели.
nlinfit - Нелинейный метод наименьших квадратов (метод Гаусса-Ньютона)
Синтаксис
beta = nlinfit(x,y,FUN,beta0)
[beta,r,J] = nlinfit(X,y,FUN,beta0)
Описание
beta = nlinfit(x,y,FUN,beta0) функция служит для расчета точечных оценок коэффициентов произвольной нелинейной регрессионной модели методом наименьших квадратов. y – вектор значений зависимой переменой, x – матрица значений независимых переменных, beta0 – вектор начальных значений искомых коэффициентов регрессионной модели, FUN – указатель на функцию, реализующую регрессионную модель. Значения независимых переменных определяются столбцами матрицы х. Количество строк матрицы x должно быть равно числу элементов вектора y. Уравнение регрессии задается как функция в следующем виде:
yhat = FUN (beta,X),
где beta – вектор коэффициентов регрессионной модели, Х –матрица независимых переменных, yhat – вектор или матрица значений зависимой переменной.
Вектор начальных значений коэффициентов регрессионной модели beta0 может быть задан произвольным массивом. Основное требование - форма представления beta0 должна совпадать со спецификацией входного аргумента beta функции FUN.
[beta,r,J] = nlinfit(X,y,FUN,beta0) функция возвращает точечные оценки коэффициентов регрессионной модели beta, r – вектор остатков, J – матрица Якоби. Параметры beta, r, J используются как входные аргументы функций nlpredci и nlparci для расчета доверительных интервалов регрессионной модели и доверительных интервалов коэффициентов модели соответственно.
Примеры использования функции nlinfit
1. Расчет параметров полной квадратической регрессионной модели вида:
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() - зависимая переменная;
- зависимая переменная; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Создается m-файл функции (polynom.m) реализующий квадратическую регрессионную модель
function yhat = polynom (beta,x)
% разделение вектора коэффициентов beta по отдельным переменным ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
A = beta(1);
B = beta(2);
C = beta(3);
D = beta(4);
E = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
x1 = x(:,1);
x2 = x(:,2);
% выражение для регрессионной модели
yhat = A.* x1.^2+B.* x2.^2+C.* x1+D.* x2+E;
1.2. Моделирование экспериментальных данных
>> A=1;
>> B=-2;
>> C=-1.5;
>> D=2.6;
>> E=2;
>> X1=[1 1 10 10 1 5.5 10 5.5 5.5];
>> X2=[2 20 20 2 11 20 11 2 11 ];
>> Y = A.* X1.^2+B.*X2.^2+C.*X1+D.*X2+E;
>> XX1=normrnd(0,1,length(X1),1);
>> XX2=unifrnd(-0.1,0.1, length(X2),1);
>> YY=normrnd(0,2, length(Y),1);
>> X1= X1+ XX1';
>> X2= X2+ XX2';
>> Y= Y+ YY';
1.3. Начальные значения коэффициентов
>> beta0=[0.1 1 0 1 1];
1.4. Расчет точечных оценок коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
>> [beta,r,J] = nlinfit([X1' X2'],Y',@polynom,beta0)
beta =
1.0542
-2.0108
-1.2157
2.1291
5.8495
r =
-4.4656
6.6490
-3.7031
14.6121
2.7691
-2.8327
-3.1220
-10.0119
0.1056
J =
0.4430 4.3682 -0.6656 2.0900 1.0000
1.2664 397.8520 1.1253 19.9462 1.0000
105.8363 400.8552 10.2877 20.0214 1.0000
78.3850 3.9888 8.8535 1.9972 1.0000
4.8001 122.7278 2.1909 11.0783 1.0000
44.7449 402.0995 6.6892 20.0524 1.0000
99.2488 120.8085 9.9624 10.9913 1.0000
33.9573 3.6241 5.8273 1.9037 1.0000
32.2015 122.4183 5.6746 11.0643 1.0000
1.5. Графическое представление полученной зависимости
>> [Xx1 Xx2]=meshgrid([1:0.5:10],[2:0.5:20]);
>> z= beta(1).*Xx1.^2+ beta(2).*Xx2.^2+ beta(3).*Xx1+ beta(4).*Xx2+ beta(5);
>> plot3(X1,X2,Y,'o',1X,2X,z)
>> grid on
.jpg)
2. Расчет коэффициентов нелинейной регрессионной модели Хогена-Ватсона для описания кинетики химической реакции. Модель Хогена-Ватсона имеет вид
![]() ,
,
где ![]() - зависимая переменная, характеризующая скорость прохождения химической реакции;
- зависимая переменная, характеризующая скорость прохождения химической реакции; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() ,
, ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Создается m-файл функции (hougen.m) реализующий регрессионную модель Хогена-Ватсона
function yhat = hougen(beta,x)
% разделение вектора коэффициентов beta по отдельным переменным b1, b2, b3, b4, b5
b1 = beta(1);
b2 = beta(2);
b3 = beta(3);
b4 = beta(4);
b5 = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
% х3 соответствующим 3-м независимым переменным
x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);
% выражение для функции Хогена
yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);
2.2. Создается вектор начальных значений коэффициентов регрессионной модели
>> beta=[1 2 1 2 1];
2.3. Загрузка матицы независимых и вектора значений зависимой переменных
>> load reaction
2.4. Вызов функции nlinfit и расчет коэффициентов регрессионной модели Хогена-Ватсона
>> betafit = nlinfit(reactants,rate,@hougen,beta)
betafit =
1.2526
0.0628
0.0400
0.1124
1.1914
2.5. Расчет коэффициентов регрессионной модели Хогена, вектора остатков и матрицы Якоби
>> [beta,r,J] = nlinfit(reactants,rate,@hougen,beta)
beta =
1.2526
0.0628
0.0400
0.1124
1.1914
r =
0.1321
-0.1642
-0.0909
0.0310
0.1142
0.0498
-0.0262
0.3115
-0.0292
0.1096
0.0716
-0.1501
-0.3026
J =
6.8739 -90.6536 -57.8640 -1.9288 0.1614
3.4454 -48.5357 -13.6240 -1.7030 0.3034
5.3563 -41.2099 -26.3042 -10.5217 1.5095
1.6950 0.1091 0.0186 0.0279 1.7913
2.2967 -35.5658 -6.0537 -0.7567 0.2023
11.8670 -89.5655 -170.1745 -8.9566 0.4400
4.4973 -14.4262 -11.5409 -9.3770 2.5744
4.1831 -41.7896 -16.8937 -5.7794 1.0082
11.8286 -51.3721 -154.1164 -27.7410 1.5001
9.1514 -25.5948 -76.7844 -30.7138 2.5790
3.3373 0.0900 0.0720 0.1080 3.5269
9.3663 -102.0611 -107.4327 -3.5811 0.2200
4.7512 -24.4631 -16.3087 -10.3002 2.1141
nnls - Решение системы линейных уравнений методом наименьших квадратов для неотрицательных значений аргумента
Синтаксис
x = nnls(A,b)
x = nnls(A,b,tol)
[x,w] = nnls(A,b)
[x,w] = nnls(A,b,tol)
Описание
x = nnls(A,b) функция предназначена для решения системы уравнений ![]() по методу наименьших квадратов при условии, что вектор решений x должен содержать неотрицательные элементы;
по методу наименьших квадратов при условии, что вектор решений x должен содержать неотрицательные элементы; ![]() , i=1..n. Вектор аргументов (решений) x минимизирует норму
, i=1..n. Вектор аргументов (решений) x минимизирует норму ![]() для
для ![]() .
.
x = nnls(A,b,tol) функция предназначена для решения системы уравнений ![]() по методу наименьших квадратов при условии, что вектор решений x должен содержать неотрицательные элементы с заданной точностью tol. По умолчанию значение tol рассчитывается как max(size(A))*norm(A,1)*eps.
по методу наименьших квадратов при условии, что вектор решений x должен содержать неотрицательные элементы с заданной точностью tol. По умолчанию значение tol рассчитывается как max(size(A))*norm(A,1)*eps.
[x,w] = nnls(A,b) функция возвращает вектор индикаторов w, элементы которого принимают значения ![]() если
если ![]() , и
, и ![]() при
при ![]() .
.
[x,w] = nnls(A,b,tol) функция предназначена для решения системы уравнений ![]() по методу наименьших квадратов при условии, что вектор решений x должен содержать неотрицательные элементы с заданной точностью tol и возвращает вектор индикаторов w.
по методу наименьших квадратов при условии, что вектор решений x должен содержать неотрицательные элементы с заданной точностью tol и возвращает вектор индикаторов w.
Примечание: Функция nnls была заменена на функцию lsqnonneg в MATLAB 5.3. В MATLAB 6.0-6.5R1 nnls выдает предупреждение и вызывает функцию lsqnonneg.
Примеры использования функции nnls
Сравнение решения системы уравнений методом наименьших квадратов (МНК) - C\d' и МНК с ограничением на неотрицательные значения решений - lsqnonneg(C,d').
>> C=[0.0372 0.2869; 0.6861 0.7071; 0.6233 0.6245; 0.6344 0.6170]
C =
0.0372 0.2869
0.6861 0.7071
0.6233 0.6245
0.6344 0.6170
>> d=[0.8587 0.1781 0.0747 0.8405]
d =
0.8587 0.1781 0.0747 0.8405
>> [C\d' lsqnonneg(C,d')]
ans =
-2.5627 0
3.1108 0.6929
>> [norm(C*(C\d')-d') norm(C*lsqnonneg(C,d')-d')]
ans =
0.6674 0.9118
Из анализа предыдущего выражения следует, что величина остатка для lsqnonneg(C,d') больше, чем для МНК без ограничений. Однако основным преимуществом последнего является отсутствие отрицательных значений в решении.
nlintool - График прогнозируемых значений
Синтаксис
nlintool(x,y,FUN,beta0,alpha)
nlintool(x,y,FUN,beta0,alpha,'xname','yname')
Описание
nlintool(x,y,FUN,beta0) функция позволяет получить интерактивный график нелинейной регрессионной модели, определяемой функцией FUN, границ ее 95% доверительного интервала для матрицы независимых переменных x и вектора зависимой переменной y. Количество строк матрицы x должно быть равно числу элементов вектора y. Входной аргумент beta0 является вектором начальных значений коэффициентов нелинейной модели FUN. Уравнение регрессии задается как функция в следующем виде:
yhat = FUN (beta,X),
где beta - вектор коэффициентов функции, Х - матрица независимых переменных, yhat - вектор или матрица выходных значений.
Вектор начальных значений коэффициентов регрессионной модели beta0 может быть задан в произвольной форме. Основное требование - форма представления beta0 должна совпадать со спецификацией входного аргумента beta функции FUN.
nlintool явным образом вызывает nlinfit. Поэтому формат входных параметров x, y, FUN, beta0 этих функций должен совпадать. Подробно определение параметров x, y, FUN, beta0 см. в описании nlinfit.
Результатом работы функции nlintool является интерактивный график (рис. 1).
.jpg)
Рис. 1. Графическое окно интерактивного нелинейного регрессионного анализа
nlintool отображает "вектор" графиков, каждый из которых соответствует столбцу матрицы независимых переменных. Штриховые линии на графиках служат для задания текущих значений независимых переменных и расчета по ним зависимой переменной. Щелчком левой кнопки мыши можно изменить положение штриховой линии на соответствующем графике и изменить значение соответствующей независимой переменной. Значение переменной отклика будет пересчитано при интерактивном изменении хотя бы одной независимой переменной регрессионной модели в графическом окне. Также величина независимой переменной может быть изменена вводом числа в строку ввода под графиком соответствующей независимой переменной. Рассчитанное значение независимой переменной и границ ее доверительных интервалов приводится в левой части интерактивного графика.
Кнопка Export графического окна используется для экспорта рассчитанных переменных в рабочую область MATLAB. При выборе кнопки Export в среду MATLAB будут экспортированы следующие переменные (рис. 2):
1. вектор точечных оценок коэффициентов регрессионной модели - Parameters;
2. матрица интервальных оценок коэффициентов регрессионной модели - Parameters CI;
3. точечная оценка зависимой переменной - Prediction;
4. вектор интервальных оценок зависимой переменной - Prediction;
5. значение корня квадратного из средней квадратической ошибки регрессионной модели - RMSE;
6. вектор остатков - Residuals.
.jpg)
Рис. 2. Диалоговое окно экспорта результатов интерактивного графического анализа.
В диалоговом окне (рис. 2) в строках ввода приведены идентификаторы переменных по умолчанию. Идентификаторы перечисленных выше переменных могут быть изменены пользователем.
Кнопка Close служит для закрытия графического окна (рис. 1).
Меню Bounds (рис. 3) позволяет задать способ расчета доверительных интервалов. Пункты Simultaneous и Non-Simultaneous определяют, каким образом по отношению к независимым переменным будут рассчитываться границы доверительного интервала: Simultaneous - в диапазоне изменения независимых переменных х; Non-Simultaneous - по выборочным значениям х(j,:). Пункты: Curve задает расчет значений доверительного интервала по регрессионной модели, Observation - по выборочным значениям y. Пункт None служит для отмены расчета границ доверительного интервала зависимой переменной и их отображения на графиках (рис. 1).
.jpg)
Рис. 3. Состав меню Bounds.
nlintool,beta0,alpha) входной аргумент alpha определяет значение уровня значимости. Доверительная вероятность определяется как 100(1-alpha)%. По умолчанию alpha принимается равным 0,05.
nlintool(x,y,FUN,beta0,alpha,'xname','yname') входные аргументы 'xname' и 'yname' определяют названия независимых переменных, столбцов матрицы х, и зависимой переменной y. 'yname' задается как строка, 'xname' - как вектор строк. Названия независимых и зависимой переменных отображаются в графическом окне (рис. 1).
Примеры использования функции nlintool
Расчет коэффициентов нелинейной регрессионной модели Хогена-Ватсона для описания кинетики химической реакции. Модель Хогена-Ватсона имеет вид
![]() ,
,
где ![]() - зависимая переменная, характеризующая скорость прохождения химической реакции;
- зависимая переменная, характеризующая скорость прохождения химической реакции; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() ,
, ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1. Создается m-файл функции (hougen.m) реализующий регрессионную модель Хогена-Ватсона
function yhat = hougen(beta,x)
% разделение вектора коэффициентов beta по отдельным переменным b1, b2, b3, b4, b5
b1 = beta(1);
b2 = beta(2);
b3 = beta(3);
b4 = beta(4);
b5 = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
% х3 соответствующим 3-м независимым переменным
x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);
% выражение для функции Хогена
yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);
2. Задается вектор начальных значений коэффициентов регрессионной модели
>> beta=[1 2 1 2 1];
3. Загрузка матицы независимых и вектора значений зависимой переменных
>> load reaction
4. Вызов функции интерактивного нелинейного регрессионного анализа nlintool Границы доверительного интервала рассчитываются для 95% доверительной вероятности.
>> nlintool(reactants,rate,@hougen,beta)
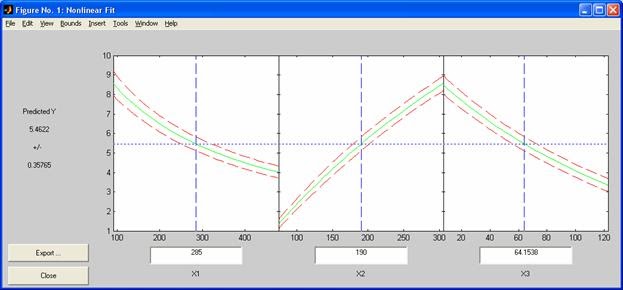
5. Экспорт параметров модели Хогена. Идентификаторы переменных приведены на следующем рисунке.
>> beta
beta =
1.2526
0.0628
0.0400
0.1124
1.1914
>> betaci
betaci =
-0.7467 3.2519
-0.0377 0.1632
-0.0312 0.1113
-0.0609 0.2857
-0.7381 3.1208
>> residuals
residuals =
0.1321
-0.1642
-0.0909
0.0310
0.1142
0.0498
-0.0262
0.3115
-0.0292
0.1096
0.0716
-0.1501
-0.3026
>> rmse
rmse =
0.1933
>> ypred
ypred =
5.4622
>> ypredci
ypredci =
5.1045 5.8199
5. Интерактивный нелинейный регрессионный анализ nlintool Границы доверительного интервала рассчитываются для 99% доверительной вероятности. Для зависимой и независимых переменных заданы метки.
>> alpha=0.01;
>> yname=['Reaction Rate'];
>> xnames=['Hydrogen '; 'n-Pentane '; 'Isopentane'];
>> nlintool(reactants,rate,@hougen,beta,alpha,xnames, yname)
.jpg)
Границы доверительного интервала зависимой переменной пересчитаны по выборочным значениям независимых переменных - Non-Simultaneous и по выборочным значениям зависимой переменной - Observation:
.jpg)
Графическое представление для установленных выше параметров расчета границ доверительного интервала приведено на следующем рисунке
.jpg)
nlparci - Вектор доверительных интервалов для параметров модели
Синтаксис
ci = nlparci(beta,r,J)
Описание
ci = nlparci(beta,r,J) функция предназначена для расчета 95% границ доверительного интервала ci коэффициентов нелинейного уравнения регрессии beta для вектора остатков r и матрицы Якоби J. Вектор коэффициентов beta рассчитывается по методу наименьших квадратов. Входные аргументы beta, r, J могут быть рассчитаны с помощью функции nlinfit.
Границы 95% доверительных интервалов коэффициентов регрессионной модели будут представлены в виде матрицы ci. Размерность ci - m×2, где m - число строк. Количество строк ci будет равно числу коэффициентов регрессионной модели beta. В первом столбце ci приводятся нижние границы доверительных интервалов, во втором - верхние границы.
Примеры использования функции nlparci
1. Расчет параметров квадратической регрессионной модели вида:
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() - зависимая переменная;
- зависимая переменная; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Создается m-файл функции (polynom.m) реализующий полную квадратическую регрессионную модель
function yhat = polynom (beta,x)
% разделение вектора коэффициентов beta по отдельным переменным ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
A = beta(1);
B = beta(2);
C = beta(3);
D = beta(4);
E = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
x1 = x(:,1);
x2 = x(:,2);
% выражение для регрессионной модели
yhat = A.* x1.^2+B.* x2.^2+C.* x1+D.* x2+E;
1.2. Моделирование экспериментальных данных
>> A=1;
>> B=-2;
>> C=-1.5;
>> D=2.6;
>> E=2;
>> X1=[1 1 10 10 1 5.5 10 5.5 5.5];
>> X2=[2 20 20 2 11 20 11 2 11 ];
>> Y = A.* X1.^2+B.*X2.^2+C.*X1+D.*X2+E;
>> YY=normrnd(0,2, length(Y),1);
>> Y= Y+ YY';
1.3. Начальные значения коэффициентов
>> beta0=[0.1 1 0 1 1];
1.4. Расчет точечных оценок коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
>> [beta,r,J] = nlinfit([X1' X2'],Y',@polynom,beta0)
beta =
0.8450
-2.0084
0.0928
2.8463
-0.8191
r =
0.7311
-1.8486
1.4182
-0.7367
1.1175
0.4304
-0.6815
0.0056
-0.4360
J =
1.0000 4.0000 1.0000 2.0000 1.0000
1.0000 400.0000 0.9999 20.0000 1.0000
100.0000 400.0000 10.0000 20.0000 1.0000
100.0000 4.0000 10.0000 2.0000 1.0000
1.0000 121.0000 1.0000 11.0000 1.0000
30.2500 400.0000 5.5000 20.0000 1.0000
100.0000 121.0000 10.0000 11.0000 1.0000
30.2500 4.0000 5.5000 2.0000 1.0000
30.2500 121.0000 5.5000 11.0000 1.0000
1.5. Расчет границ 95% доверительного интервала коэффициентов квадратической регрессионной модели
>> ci = nlparci(beta,r,J)
ci =
0.7029 0.9871
-2.0439 -1.9729
-1.5134 1.6990
2.0432 3.6494
-5.4472 3.8090
1.6. Графическое представление полученной зависимости
>> [Xx1 Xx2]=meshgrid([1:0.5:10],[2:0.5:20]);
>> z= beta(1).*Xx1.^2+ beta(2).*Xx2.^2+ beta(3).*Xx1+ beta(4).*Xx2+ beta(5);
>> zn= ci(1,1).*Xx1.^2+ ci(2,1).*Xx2.^2+ ci(3,1).*Xx1+ ci(4,1).*Xx2+ ci(5,1);
>> zv= ci(1,2).*Xx1.^2+ ci(2,2).*Xx2.^2+ ci(3,2).*Xx1+ ci(4,2).*Xx2+ ci(5,2);
>> plot3(X1,X2,Y,'o',Xx1,Xx2,z)
>> grid on
.jpg)
>> plot3(X1,X2,Y,'o',Xx1,Xx2,zn)
>> grid on
.jpg)
>> plot3(X1,X2,Y,'o',Xx1,Xx2,zv)
>> grid on
.jpg)
2. Расчет коэффициентов нелинейной регрессионной модели Хогена-Ватсона и границ их доверительных интервалов для описания кинетики химической реакции. Модель Хогена-Ватсона имеет вид
![]() ,
,
где ![]() - зависимая переменная, характеризующая скорость прохождения химической реакции;
- зависимая переменная, характеризующая скорость прохождения химической реакции; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() ,
, ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Создается m-файл функции (hougen.m) реализующий регрессионную модель Хогена-Ватсона
function yhat = hougen(beta,x)
% разделение вектора коэффициентов beta по отдельным переменным b1, b2, b3, b4, b5
b1 = beta(1);
b2 = beta(2);
b3 = beta(3);
b4 = beta(4);
b5 = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
% х3 соответствующим 3-м независимым переменным
x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);
% выражение для функции Хогена
yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);
2.2. Создается вектор начальных значений коэффициентов регрессионной модели
>> beta=[1 2 1 2 1];
2.3. Загрузка матицы независимых и вектора значений зависимой переменных
>> load reaction
2.4. Расчет коэффициентов регрессионной модели Хогена, вектора остатков и матрицы Якоби
>> [beta,r,J] = nlinfit(reactants,rate,@hougen,beta)
beta =
1.2526
0.0628
0.0400
0.1124
1.1914
r =
0.1321
-0.1642
-0.0909
0.0310
0.1142
0.0498
-0.0262
0.3115
-0.0292
0.1096
0.0716
-0.1501
-0.3026
J =
6.8739 -90.6536 -57.8640 -1.9288 0.1614
3.4454 -48.5357 -13.6240 -1.7030 0.3034
5.3563 -41.2099 -26.3042 -10.5217 1.5095
1.6950 0.1091 0.0186 0.0279 1.7913
2.2967 -35.5658 -6.0537 -0.7567 0.2023
11.8670 -89.5655 -170.1745 -8.9566 0.4400
4.4973 -14.4262 -11.5409 -9.3770 2.5744
4.1831 -41.7896 -16.8937 -5.7794 1.0082
11.8286 -51.3721 -154.1164 -27.7410 1.5001
9.1514 -25.5948 -76.7844 -30.7138 2.5790
3.3373 0.0900 0.0720 0.1080 3.5269
9.3663 -102.0611 -107.4327 -3.5811 0.2200
4.7512 -24.4631 -16.3087 -10.3002 2.1141
2.5. Расчет границ 95% доверительного интервала коэффициентов регрессионной модели Хогена
>> ci = nlparci(beta,r,J)
ci =
-0.7467 3.2519
-0.0377 0.1632
-0.0312 0.1113
-0.0609 0.2857
-0.7381 3.1208
nlpredci - Прогнозируемые значения и их доверительные интервалы
Синтаксис
ypred = nlpredci(FUN,inputs,beta,r,J)
[ypred,delta] = nlpredci(FUN,inputs,beta,r,J)
ypred = nlpredci(FUN,inputs,beta,r,J,alpha,'simopt','predopt')
Описание
ypred = nlpredci(FUN,inputs,beta,r,J) функция возвращает вектор значений зависимой переменной ypred регрессионной модели FUN рассчитанные по матрице независимых переменных inputs, коэффициентам регрессионной модели beta, вектору остатков r и матрице Якоби J. Значения независимых переменных расположены по столбцам матрицы inputs. Количество строк матрицы inputs и число элементов вектора y будет одинаковым.
Уравнение регрессии задается как m-функция в следующем виде:
yhat = FUN (beta0,X),
где beta0 - вектор коэффициентов функции, Х -матрица независимых переменных, yhat - вектор или матрица выходных значений.
Вектор значений коэффициентов регрессионной модели beta функции nlpredci может быть задан в произвольной форме. Основное требование - форма представления beta должна совпадать со спецификацией входного аргумента beta0 функции FUN.
[ypred,delta] = nlpredci(FUN,inputs,beta,r,J) функция возвращает векторы значений ypred и ½ доверительного интервала delta зависимой переменной. Доверительный интервал рассчитывается для 95% доверительной вероятности. Доверительный интервал определяется как [ypred-delta, ypred+delta] и рассчитывается в точках inputs(j,:) независимой переменной по полученному равнению регрессии.
ypred = nlpredci(FUN,inputs,beta,r,J,alpha,'simopt','predopt') дополнительные входные параметры alpha, 'simopt', 'predopt' позволяют управлять видом рассчитываемого доверительного интервала. alpha - уровень значимости доверительного интервала. Доверительная вероятность определяется как 100(1-alpha)%. 'simopt' определяет каким образом, по отношению к независимым переменным, будут рассчитываться границы доверительного интервала: 'on' - в диапазоне изменения независимых переменных inputs; 'off' - в выборочных значениях inputs(j,:). Значение по умолчанию 'simopt'='off'. Входной аргумент 'predopt' - позволяет задать: 'curve' - расчет значений доверительного интервала по регрессионной модели; 'observation' - расчет значений доверительного интервала по выборочным значениям. Значение по умолчанию 'predopt'='curve'.
Входные параметры beta, r, J могут быть рассчитаны с использованием функции nlinfit. Формат задания функции FUN см. в описании nlinfit.
Примеры использования функции nlpredci
1. Расчет значений зависимой переменной и границ доверительных интервалов полной квадратической регрессионной модели вида:
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() - зависимая переменная;
- зависимая переменная; ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
1.1. Создается m-файл функции (polynom.m) реализующий полную квадратическую регрессионную модель
function yhat = polynom (beta,x)
% разделение вектора коэффициентов beta по отдельным переменным ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
A = beta(1);
B = beta(2);
C = beta(3);
D = beta(4);
E = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
x1 = x(:,1);
x2 = x(:,2);
% выражение для регрессионной модели
yhat = A.* x1.^2+B.* x2.^2+C.* x1+D.* x2+E;
1.2. Моделирование экспериментальных данных
>> A=1;
>> B=-2;
>> C=-1.5;
>> D=2.6;
>> E=2;
>> X1=[1 1 10 10 1 5.5 10 5.5 5.5];
>> X2=[2 20 20 2 11 20 11 2 11 ];
>> Y = A.* X1.^2+B.*X2.^2+C.*X1+D.*X2+E;
>> XX1=normrnd(0,1,length(X1),1);
>> XX2=unifrnd(-0.1,0.1, length(X2),1);
>> YY=normrnd(0,2, length(Y),1);
>> X1= X1+ XX1';
>> X2= X2+ XX2';
>> Y= Y+ YY';
1.3. Начальные значения коэффициентов
>> beta0=[0.1 1 0 1 1];
1.4. Расчет точечных оценок коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
>> [beta,r,J] = nlinfit([X1' X2'],Y',@polynom,beta0)
beta =
0.7949
-1.9789
-0.4308
1.9825
5.3885
r =
-1.8501
-5.1480
11.4807
1.8753
7.8970
-6.4160
-8.9814
-0.0211
1.1635
J =
0.3220 4.3682 0.5674 2.0900 1.0000
0.4430 397.8520 -0.6656 19.9462 1.0000
102.5224 400.8552 10.1253 20.0214 1.0000
105.8363 3.9888 10.2877 1.9972 1.0000
0.0215 122.7278 -0.1465 11.0783 1.0000
44.7684 402.0995 6.6909 20.0524 1.0000
125.1974 120.8085 11.1892 10.9913 1.0000
29.8375 3.6241 5.4624 1.9037 1.0000
33.9573 122.4183 5.8273 11.0643 1.0000
1.5. Матрица значений независимых переменных, для которых рассчитываются значения зависимой переменной
>> XX1=min(X1):(max(X1)- min(X1))/20: max(X1);
>> XX2=min(X2):(max(X2)- min(X2))/20: max(X2);
>> inputs=[ XX1' XX2'];
1.6. Расчет значений зависимой переменной Yr и нижней YN и верхней YV границ 95% доверительного интервала
>> [Yr, delta]= nlpredci(@polynom,inputs,beta,r,J)
Yr =
2.6299
-4.6407
-14.6118
-27.2833
-42.6553
-60.7276
-81.5004
-104.9736
-131.1473
-160.0214
-191.5959
-225.8708
-262.8462
-302.5220
-344.8982
-389.9749
-437.7520
-488.2295
-541.4075
-597.2859
-655.8647
delta =
22.6018
18.4946
15.8715
14.8363
15.1253
16.1972
17.5411
18.8157
19.8238
20.4581
20.6653
20.4279
19.7586
18.7048
17.3664
15.9327
14.7407
14.3158
15.2390
17.8026
21.8913
>> YN=Yr-delta
YN =
-19.9719
-23.1353
-30.4833
-42.1196
-57.7805
-76.9248
-99.0415
-123.7894
-150.9711
-180.4795
-212.2612
-246.2988
-282.6048
-321.2268
-362.2647
-405.9076
-452.4927
-502.5454
-556.6465
-615.0884
-677.7560
>> YV=Yr+delta
YV =
25.2317
13.8539
1.2597
-12.4470
-27.5300
-44.5304
-63.9593
-86.1579
-111.3235
-139.5633
-170.9306
-205.4429
-243.0876
-283.8172
-327.5318
-374.0422
-423.0113
-473.9137
-526.1685
-579.4833
-633.9734
1.7. Графическое представление полученной зависимости
>> [X_1 X_2]=meshgrid([1:0.5:10],[2:0.5:20]);
>> z= beta(1).*X_1.^2+ beta(2).*X_2.^2+ beta(3).*X_1+ beta(4).*X_2+ beta(5);
>> plot3(XX1,XX2,YN,'ro', XX1,XX2,YV,'g+',X_1,X_2,z)
>> grid on
.jpg)
2. Расчет значений зависимой переменной и границ доверительных интервалов регрессионной модели Хогена-Ватсона при оценке кинетики химической реакции. Модель Хогена-Ватсона имеет вид
![]() ,
,
где ![]() - зависимая переменная, характеризующая скорость прохождения химической реакции;
- зависимая переменная, характеризующая скорость прохождения химической реакции; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - параметры регрессионной модели;
- параметры регрессионной модели; ![]() ,
, ![]() ,
, ![]() - независимые переменные.
- независимые переменные.
2.1. Создается m-файл функции (hougen.m) реализующий регрессионную модель Хогена-Ватсона
function yhat = hougen(beta,x)
% разделение вектора коэффициентов beta по отдельным переменным b1, b2, b3, b4, b5
b1 = beta(1);
b2 = beta(2);
b3 = beta(3);
b4 = beta(4);
b5 = beta(5);
% разделение матрицы независимых переменных х по отдельным векторам х1, х2,
% х3 соответствующим 3-м независимым переменным
x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);
% выражение для функции Хогена
yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);
2.2. Создается вектор начальных значений коэффициентов регрессионной модели
>> beta=[1 2 1 2 1];
2.3. Загрузка матицы независимых и вектора значений зависимой переменных
>> load reaction
2.4. Расчет коэффициентов регрессионной модели Хогена, вектора остатков и матрицы Якоби
>> [beta,r,J] = nlinfit(reactants,rate,@hougen,beta)
beta =
1.2526
0.0628
0.0400
0.1124
1.1914
r =
0.1321
-0.1642
-0.0909
0.0310
0.1142
0.0498
-0.0262
0.3115
-0.0292
0.1096
0.0716
-0.1501
-0.3026
J =
6.8739 -90.6536 -57.8640 -1.9288 0.1614
3.4454 -48.5357 -13.6240 -1.7030 0.3034
5.3563 -41.2099 -26.3042 -10.5217 1.5095
1.6950 0.1091 0.0186 0.0279 1.7913
2.2967 -35.5658 -6.0537 -0.7567 0.2023
11.8670 -89.5655 -170.1745 -8.9566 0.4400
4.4973 -14.4262 -11.5409 -9.3770 2.5744
4.1831 -41.7896 -16.8937 -5.7794 1.0082
11.8286 -51.3721 -154.1164 -27.7410 1.5001
9.1514 -25.5948 -76.7844 -30.7138 2.5790
3.3373 0.0900 0.0720 0.1080 3.5269
9.3663 -102.0611 -107.4327 -3.5811 0.2200
4.7512 -24.4631 -16.3087 -10.3002 2.1141
2.5. Матрица значений независимых переменных, для которых рассчитываются значения зависимой переменной
>> X1=min(reactants(:,1)):(max(reactants(:,1))- min(reactants(:,1)))/20: max(reactants(:,1));
>> X2=min(reactants(:,2)):(max(reactants(:,2))- min(reactants(:,2)))/20: max(reactants(:,2));
>> X3=min(reactants(:,3)):(max(reactants(:,3))- min(reactants(:,3)))/20: max(reactants(:,3));
>> inputs=[X1' X2' X3'];
2.6. Расчет значений зависимой переменной Rrate и нижней rateN и верхней rateV границ 95% доверительного интервала
>> [Rrate, delta]= nlpredci(@hougen,inputs,beta,r,J)
Rrate =
7.9112
7.3034
6.8639
6.5312
6.2706
6.0610
5.8887
5.7446
5.6223
5.5172
5.4259
5.3458
5.2750
5.2120
5.1556
5.1047
5.0586
5.0167
4.9784
4.9432
4.9109
delta =
0.7422
0.5570
0.4400
0.3620
0.3081
0.2701
0.2429
0.2233
0.2092
0.1990
0.1916
0.1864
0.1827
0.1801
0.1784
0.1772
0.1766
0.1763
0.1762
0.1764
0.1766
>> rateN=Rrate-delta
rateN =
7.1689
6.7464
6.4239
6.1692
5.9625
5.7909
5.6458
5.5213
5.4131
5.3182
5.2342
5.1594
5.0924
5.0319
4.9772
4.9275
4.8820
4.8404
4.8022
4.7669
4.7342
>> rateV=Rrate+delta
rateV =
8.6534
7.8605
7.3039
6.8932
6.5787
6.3311
6.1316
5.9679
5.8315
5.7161
5.6175
5.5322
5.4577
5.3921
5.3339
5.2820
5.2352
5.1930
5.1546
5.1196
5.0875
2.7. Расчет значений зависимой переменной Rrate и нижней rateN и верхней rateV границ 99% доверительного интервала по диапазонам изменения значений независимых переменных ('simopt'='off') для выборочных значений зависимой переменной ('predopt'='observation').
>> alpha=0.01;
>> simop='off';
>> predopt='observation';
>> [Rrate, delta]= nlpredci(@hougen,inputs,beta,r,J,alpha,simop,predopt)
Rrate =
7.9112
7.3034
6.8639
6.5312
6.2706
6.0610
5.8887
5.7446
5.6223
5.5172
5.4259
5.3458
5.2750
5.2120
5.1556
5.1047
5.0586
5.0167
4.9784
4.9432
4.9109
delta =
1.2598
1.0380
0.9113
0.8355
0.7885
0.7584
0.7386
0.7254
0.7165
0.7103
0.7060
0.7030
0.7009
0.6995
0.6986
0.6980
0.6976
0.6975
0.6974
0.6975
0.6976
>> rateN=Rrate-delta
rateN =
6.6514
6.2654
5.9526
5.6957
5.4822
5.3026
5.1501
5.0192
4.9058
4.8069
4.7199
4.6428
4.5741
4.5125
4.4570
4.4067
4.3610
4.3193
4.2810
4.2457
4.2132
>> rateV=Rrate+delta
rateV =
9.1709
8.3415
7.7752
7.3667
7.0591
6.8194
6.6274
6.4700
6.3387
6.2274
6.1318
6.0488
5.9760
5.9115
5.8542
5.8027
5.7563
5.7142
5.6758
5.6407
5.6085
bbdesign - Генерация матрицы плана Бокса-Бенкина
Синтаксис
D = bbdesign(nfactors)
D = bbdesign(nfactors,'pname1',pvalue1,'pname2',pvalue2,...)
[D,blk] = bbdesign(...)
Описание
D = bbdesign(nfactors) функция позволяет получить матрицу D плана Бокса-Бенкина для nfactors факторов. Размерность матрицы плана эксперимента D равна nfactors x nfactors. Количество опытов в матрице равно числу факторов. Элементами матрицы D являются 1 и -1 кодирующие максимальные и минимальные значения факторов соответственно.
[D,blk] = bbdesign(nfactors) в отличии от первого варианта синтаксиса функция возвращает вектор blk номеров блоков опытов. Блоки позволяют сгруппировать опыты таким образом, чтобы минимизировать влияние изменений внешних условий на значения оцениваемых параметров.
[...] = bbdesign(nfactors,'pname1',pvalue1,'pname2',pvalue2,...) такой вариант синтаксиса функции позволяет задать дополнительные параметры 'pname' и их значения pvalue:
-
'center' - количество повторений опытов в центральных точках плана;
-
'blocksize' - максимальное количество точек в блоке плана.
Дополнительные аргументы задаются в виде пары: 'название параметра', значение параметра.
Примечание: в работах Бокса и Бенкина предложены планы для числа факторов 3-7, 9-12, 16. Для указанного числа факторов функция bbdesign генерирует матрицы планов экспериментов согласно Боксу и Бенкину. Для числа факторов отличного от приведенных значений матрица плана рассчитывается по алгоритму аналогичному изложенному в работах Бокса и Бенкина.
Примеры использования функции генерации матрицы плана Бокса-Бенкина
Генерация матрицы плана Бокса-Бенкина для 3 факторов
>> D = bbdesign(3)
D =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0
Генерация матрицы плана Бокса-Бенкина для 5 факторов разделенного на блоки
>> [D,blk] = bbdesign(5)
|
D= |
blk= |
|
-1 -1 0 0 0 -1 1 0 0 0 1 -1 0 0 0 1 1 0 0 0 0 0 -1 -1 0 0 0 -1 1 0 0 0 1 -1 0 0 0 1 1 0 0 -1 0 0 -1 0 -1 0 0 1 0 1 0 0 -1 0 1 0 0 1 -1 0 -1 0 0 -1 0 1 0 0 1 0 -1 0 0 1 0 1 0 0 0 0 0 -1 -1 0 0 0 -1 1 0 0 0 1 -1 0 0 0 1 1 0 -1 -1 0 0 0 -1 1 0 0 0 1 -1 0 0 0 1 1 0 0 -1 0 0 -1 0 -1 0 0 1 0 1 0 0 -1 0 1 0 0 1 0 0 0 -1 0 -1 0 0 -1 0 1 0 0 1 0 -1 0 0 1 0 1 -1 0 0 0 -1 -1 0 0 0 1 1 0 0 0 -1 1 0 0 0 1 0 -1 0 -1 0 0 -1 0 1 0 0 1 0 -1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 2 2 2 |
Генерация матрицы плана Бокса-Бенкина для 4 факторов разделенного на блоки при условии 5 повторных опытов в центральной точке плана и максимальном числе точек в блоке плана равном 10.
>> [D,blk] = bbdesign(4, 'center', 5, 'blocksize', 10)
D =
-1 -1 0 0
-1 1 0 0
1 -1 0 0
1 1 0 0
0 0 -1 -1
0 0 -1 1
0 0 1 -1
0 0 1 1
-1 0 0 -1
-1 0 0 1
1 0 0 -1
1 0 0 1
0 -1 -1 0
0 -1 1 0
0 1 -1 0
0 1 1 0
-1 0 -1 0
-1 0 1 0
1 0 -1 0
1 0 1 0
0 -1 0 -1
0 -1 0 1
0 1 0 -1
0 1 0 1
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
blk =
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
1
1
2
2
3
Графически матрицу плана Бокса-Бенкина для 3 факторов можно представить следующим образом
>> D = bbdesign(3)
D =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0
>> x= D(:,1);
>> y= D (:,2);
>> z= D (:,3);
>> plot3(x,y,z,'o')
>> grid on
candexch - D-оптимальный план (на основе алгоритма перестановки строк для формирования множества возможных значений)
Синтаксис
rlist = candexch(C,nrows)
rlist = candexch(C,nrows,'param1',value1,'param2',value2,...)
Описание
rlist = candexch(C,nrows) функция предназначена для генерации плана эксперимента rlist из начального множества точек C в факторном пространстве на основе алгоритма перестановки строк. Матрица С, размерностью n-p, содержит значения p эффектов модели для каждой из n точек. Входной параметр nrows задает количество опытов в плане эксперимента. Выходной параметр rlist является вектором с числом элементов nrows и задает номера выбранных строк из начального множества точек C.
Функция candexch выбирает матрицу начального плана Х случайным образом. Затем на основе алгоритма замены строк Х строками начального множества точек С формируется D-оптимальный план эксперимента. Вычисления прекращаются, если будет выполнено условие ![]() , или достигнуто максимальное число итераций.
, или достигнуто максимальное число итераций.
rlist = candexch(C,nrows,'param1',value1,'param2',value2,...) этот вариант синтаксиса функции позволяет определить следующие дополнительные входные аргументы:
|
'display' |
Вывод значения счетчика итераций. Возможные значения 'display': 'on' - вывод в командное окно, 'off' - отмена отображения. Значение по умолчанию 'on'. |
|
'init' |
Начальная матрица значений факторов с размерностью nrows?p. По умолчанию принимается случайное подмножество строк начального множества С. |
|
'maxiter' |
Максимальное число итераций. Значение по умолчанию - 10. |
Дополнительные аргументы задаются в виде пары: 'название параметра', значение параметра.
Примеры использования функции генерации матрицы D-оптимального плана из начального множества точек в факторном пространстве на основе алгоритма перестановки строк
Генерация матрицы значений факторов X D-оптимального плана из начального множества точек в факторном пространстве для 12 опытов. Начальное множество xcand генерируется при помощи функции candgen для 3 факторов и полной квадратической модели.
>> nfactors=3;
>> model='quadratic';
>> xcand = candgen(nfactors,model);
>> nrows=12;
>> rlist = candexch(xcand,nrows)
rlist =
9
1
7
3
3
7
9
1
1
7
3
9
>> X = xcand(rlist,:)
X =
1 1 -1
-1 -1 -1
-1 1 -1
1 -1 -1
1 -1 -1
-1 1 -1
1 1 -1
-1 -1 -1
-1 -1 -1
-1 1 -1
1 -1 -1
1 1 -1
Генерация матрицы D-оптимального плана Х из начального множества точек С в факторном пространстве для 12 опытов. Начальное множество С генерируется при помощи функции полного факторного эксперимента fullfact для 3 факторов на 5 уровнях. Матрица значений факторов полного факторного эксперимента приводится к единичному кубу F. На полученную матрицу значений факторов накладывается ограничение по величине построчной суммы меньше или равной 1,51: sum(F,2)<=1.51. Затем формируется матрица F со строками, удовлетворяющими указанному ограничению. Начальное множество С является матрицей значений факторов соответствующих постоянному члену, линейным и квадратическим эффектам.
>> F = (fullfact([5 5 5])-1)/4;
>> T = sum(F,2)<=1.51
>> F = F(T,:)
>> C = [ones(size(F,1),1) F F.^2]
C =
1.0000 0 0 0 0 0 0
1.0000 0.2500 0 0 0.0625 0 0
1.0000 0.5000 0 0 0.2500 0 0
1.0000 0.7500 0 0 0.5625 0 0
1.0000 1.0000 0 0 1.0000 0 0
1.0000 0 0.2500 0 0 0.0625 0
1.0000 0.2500 0.2500 0 0.0625 0.0625 0
1.0000 0.5000 0.2500 0 0.2500 0.0625 0
1.0000 0.7500 0.2500 0 0.5625 0.0625 0
1.0000 1.0000 0.2500 0 1.0000 0.0625 0
1.0000 0 0.5000 0 0 0.2500 0
1.0000 0.2500 0.5000 0 0.0625 0.2500 0
1.0000 0.5000 0.5000 0 0.2500 0.2500 0
1.0000 0.7500 0.5000 0 0.5625 0.2500 0
1.0000 1.0000 0.5000 0 1.0000 0.2500 0
1.0000 0 0.7500 0 0 0.5625 0
1.0000 0.2500 0.7500 0 0.0625 0.5625 0
1.0000 0.5000 0.7500 0 0.2500 0.5625 0
1.0000 0.7500 0.7500 0 0.5625 0.5625 0
1.0000 0 1.0000 0 0 1.0000 0
1.0000 0.2500 1.0000 0 0.0625 1.0000 0
1.0000 0.5000 1.0000 0 0.2500 1.0000 0
1.0000 0 0 0.2500 0 0 0.0625
1.0000 0.2500 0 0.2500 0.0625 0 0.0625
1.0000 0.5000 0 0.2500 0.2500 0 0.0625
1.0000 0.7500 0 0.2500 0.5625 0 0.0625
1.0000 1.0000 0 0.2500 1.0000 0 0.0625
1.0000 0 0.2500 0.2500 0 0.0625 0.0625
1.0000 0.2500 0.2500 0.2500 0.0625 0.0625 0.0625
1.0000 0.5000 0.2500 0.2500 0.2500 0.0625 0.0625
1.0000 0.7500 0.2500 0.2500 0.5625 0.0625 0.0625
1.0000 1.0000 0.2500 0.2500 1.0000 0.0625 0.0625
1.0000 0 0.5000 0.2500 0 0.2500 0.0625
1.0000 0.2500 0.5000 0.2500 0.0625 0.2500 0.0625
1.0000 0.5000 0.5000 0.2500 0.2500 0.2500 0.0625
1.0000 0.7500 0.5000 0.2500 0.5625 0.2500 0.0625
1.0000 0 0.7500 0.2500 0 0.5625 0.0625
1.0000 0.2500 0.7500 0.2500 0.0625 0.5625 0.0625
1.0000 0.5000 0.7500 0.2500 0.2500 0.5625 0.0625
1.0000 0 1.0000 0.2500 0 1.0000 0.0625
1.0000 0.2500 1.0000 0.2500 0.0625 1.0000 0.0625
1.0000 0 0 0.5000 0 0 0.2500
1.0000 0.2500 0 0.5000 0.0625 0 0.2500
1.0000 0.5000 0 0.5000 0.2500 0 0.2500
1.0000 0.7500 0 0.5000 0.5625 0 0.2500
1.0000 1.0000 0 0.5000 1.0000 0 0.2500
1.0000 0 0.2500 0.5000 0 0.0625 0.2500
1.0000 0.2500 0.2500 0.5000 0.0625 0.0625 0.2500
1.0000 0.5000 0.2500 0.5000 0.2500 0.0625 0.2500
1.0000 0.7500 0.2500 0.5000 0.5625 0.0625 0.2500
1.0000 0 0.5000 0.5000 0 0.2500 0.2500
1.0000 0.2500 0.5000 0.5000 0.0625 0.2500 0.2500
1.0000 0.5000 0.5000 0.5000 0.2500 0.2500 0.2500
1.0000 0 0.7500 0.5000 0 0.5625 0.2500
1.0000 0.2500 0.7500 0.5000 0.0625 0.5625 0.2500
1.0000 0 1.0000 0.5000 0 1.0000 0.2500
1.0000 0 0 0.7500 0 0 0.5625
1.0000 0.2500 0 0.7500 0.0625 0 0.5625
1.0000 0.5000 0 0.7500 0.2500 0 0.5625
1.0000 0.7500 0 0.7500 0.5625 0 0.5625
1.0000 0 0.2500 0.7500 0 0.0625 0.5625
1.0000 0.2500 0.2500 0.7500 0.0625 0.0625 0.5625
1.0000 0.5000 0.2500 0.7500 0.2500 0.0625 0.5625
1.0000 0 0.5000 0.7500 0 0.2500 0.5625
1.0000 0.2500 0.5000 0.7500 0.0625 0.2500 0.5625
1.0000 0 0.7500 0.7500 0 0.5625 0.5625
1.0000 0 0 1.0000 0 0 1.0000
1.0000 0.2500 0 1.0000 0.0625 0 1.0000
1.0000 0.5000 0 1.0000 0.2500 0 1.0000
1.0000 0 0.2500 1.0000 0 0.0625 1.0000
1.0000 0.2500 0.2500 1.0000 0.0625 0.0625 1.0000
1.0000 0 0.5000 1.0000 0 0.2500 1.0000
>> R = candexch(C,12)
R =
22
56
15
46
69
72
35
51
1
46
44
1
>> X = F(R,:)
X =
0.5000 1.0000 0
0 1.0000 0.5000
1.0000 0.5000 0
1.0000 0 0.5000
0.5000 0 1.0000
0 0.5000 1.0000
0.5000 0.5000 0.2500
0 0.5000 0.5000
0 0 0
1.0000 0 0.5000
0.5000 0 0.5000
0 0 0
Генерация матрицы значений факторов X D-оптимального плана из начального множества точек в факторном пространстве для 12 опытов. Начальное множество xcand генерируется при помощи функции candgen для 3 факторов и полной квадратической модели. В качестве дополнительного параметра задана матрица А начального приближения при поиске D-оптимального плана из множества xcand. Матрица А является подматрицей xcand, первые ее 12 строк.
>> nfactors=3;
>> model='quadratic';
>> xcand = candgen(nfactors,model)
xcand =
-1 -1 -1
0 -1 -1
1 -1 -1
-1 0 -1
0 0 -1
1 0 -1
-1 1 -1
0 1 -1
1 1 -1
-1 -1 0
0 -1 0
1 -1 0
-1 0 0
0 0 0
1 0 0
-1 1 0
0 1 0
1 1 0
-1 -1 1
0 -1 1
1 -1 1
-1 0 1
0 0 1
1 0 1
-1 1 1
0 1 1
1 1 1
>> nrows=12;
>> A= xcand (1: nrows,:)
A =
-1 -1 -1
0 -1 -1
1 -1 -1
-1 0 -1
0 0 -1
1 0 -1
-1 1 -1
0 1 -1
1 1 -1
-1 -1 0
0 -1 0
1 -1 0
>> rlist = candexch(xcand,nrows,'init',A)
rlist =
1
1
3
7
3
9
7
1
9
9
3
7
>> X = xcand(rlist,:)
X =
-1 -1 -1
-1 -1 -1
1 -1 -1
-1 1 -1
1 -1 -1
1 1 -1
-1 1 -1
-1 -1 -1
1 1 -1
1 1 -1
1 -1 -1
-1 1 -1
Графическое представление начального множества xcand, матрицы начального приближения А и матрицы значений факторов X.
>> x= xcand (:,1);
>> y= xcand (:,2);
>> z= xcand (:,3);
>> subplot(1,3,1)
>> plot3(x,y,z,'o')
>> grid on
>> x1= A(:,1);
>> y1= A (:,2);
>> z1= A (:,3);
>> subplot(1,3,2)
>> plot3(x1,y1,z1,'dr')
>> grid on
>> x2= X(:,1);
>> y2= X (:,2);
>> z2= X (:,3);
>> subplot(1,3,3)
>> plot3(x2,y2,z2,'+r')
>> grid on
candgen - Генерирует множество возможных сочетаний факторов соответствующих D-оптимальному плану
Синтаксис
xcand = candgen(nfactors,'model')
[xcand,fxcand] = candgen(nfactors,'model')
Описание
xcand = candgen(nfactors,'model') функция предназначена для генерации начального множества точек xcand в факторном пространстве, соответствующего D-оптимальному плану с числом факторов nfactors и видом модели регрессии 'model'. xcand является матрицей значений факторов. Матрица выходных значений xcand содержит nfactors столбцов. Предусмотрены следующие виды математической модели:
|
Значение 'model' |
Вид математической модели |
|
'linear' |
Линейная модель с постоянным членом. Значение по умолчанию. |
|
'interaction' |
Линейная модель с постоянным членом и эффектами взаимодействия. |
|
'quadratic' |
Полная квадратическая модель, включающая линейные, квадратические эффекты, эффекты взаимодействий, постоянный член. |
|
'purequadratic' |
Неполная квадратическая модель, включающая линейные, квадратические эффекты, постоянный член. |
Кроме строкового значения входной аргумент model может быть задан как вектор или матрица аналогично такому же аргументу функции x2fx. Функция x2fx позволяет выполнить преобразование матрицы значений факторов Х в матрицу плана эксперимента D. В случае, если X и model заданы как векторы, то матрица плана эксперимента формируется по правилу: каждый столбец D является последовательным возведением Х в степень элемента вектора model. Размерность матрицы D равна n?m, где n - число элементов вектора Х, m - число элементов вектора model. Т.е., вектор model является списком степеней полинома регрессионной модели для одного фактора Х. Если X и model заданы как матрицы, то столбец матрицы D формируются по формуле:
D(i,j)=prod(Х(i,:).^model(j,:)),
т.е., ij-й элемент матрицы D является произведением элементов i-й строки матрицы Х возведенных последовательно в степени j-й строки матрицы model. Таким образом, количество столбцов model должно быть равно числу столбцов матрицы Х.
[xcand,fxcand] = candgen(nfactors,model) функция возвращает матрицу значений факторов xcand и матрицу значений степеней fxcand.
Примечание: Функция rowexch генерирует начальное множество точек в факторном пространстве с помощью функции candgen и формирует матрицу D-оптимального плана с помощью функции candexch. Раздельное использование функций candgen и candexch целесообразно в случае, когда необходимо изменить начальное множество точек.
Примеры использования функции генерации начального множества точек в факторном пространстве для D-оптимального плана
Генерация начального множества в виде матрицы значений факторов D-оптимального плана для 3 факторов и полной квадратической модели
>> nfactors=3;
>> model='quadratic';
>> xcand = candgen(nfactors,model)
xcand =
-1 -1 -1
0 -1 -1
1 -1 -1
-1 0 -1
0 0 -1
1 0 -1
-1 1 -1
0 1 -1
1 1 -1
-1 -1 0
0 -1 0
1 -1 0
-1 0 0
0 0 0
1 0 0
-1 1 0
0 1 0
1 1 0
-1 -1 1
0 -1 1
1 -1 1
-1 0 1
0 0 1
1 0 1
-1 1 1
0 1 1
1 1 1
Генерация начального множества в виде матрицы значений факторов и матрицы D-оптимального плана
для 3 факторов и неполной квадратической модели
>> nfactors=3;
>> model='purequadratic';
>> [xcand,fxcand] = candgen(nfactors,model)
xcand =
-1 -1 -1
0 -1 -1
1 -1 -1
-1 0 -1
0 0 -1
1 0 -1
-1 1 -1
0 1 -1
1 1 -1
-1 -1 0
0 -1 0
1 -1 0
-1 0 0
0 0 0
1 0 0
-1 1 0
0 1 0
1 1 0
-1 -1 1
0 -1 1
1 -1 1
-1 0 1
0 0 1
1 0 1
-1 1 1
0 1 1
1 1 1
fxcand =
1 -1 -1 -1 1 1 1
1 0 -1 -1 0 1 1
1 1 -1 -1 1 1 1
1 -1 0 -1 1 0 1
1 0 0 -1 0 0 1
1 1 0 -1 1 0 1
1 -1 1 -1 1 1 1
1 0 1 -1 0 1 1
1 1 1 -1 1 1 1
1 -1 -1 0 1 1 0
1 0 -1 0 0 1 0
1 1 -1 0 1 1 0
1 -1 0 0 1 0 0
1 0 0 0 0 0 0
1 1 0 0 1 0 0
1 -1 1 0 1 1 0
1 0 1 0 0 1 0
1 1 1 0 1 1 0
1 -1 -1 1 1 1 1
1 0 -1 1 0 1 1
1 1 -1 1 1 1 1
1 -1 0 1 1 0 1
1 0 0 1 0 0 1
1 1 0 1 1 0 1
1 -1 1 1 1 1 1
1 0 1 1 0 1 1
1 1 1 1 1 1 1
Генерация начального множества в виде матрицы значений факторов и матрицы D-оптимального плана
для 3 факторов и регрессионной модели заданной в виде матрицы model.
>> nfactors=3;
>> model=[0 1 2; 0 1 2; 0 1 2; 0 1 2]
model =
0 1 2
0 1 2
0 1 2
0 1 2
>> [xcand,fxcand] = candgen(nfactors, model)
xcand =
-1 -1 -1
1 -1 -1
-1 1 -1
1 1 -1
-1 -1 0
1 -1 0
-1 1 0
1 1 0
-1 -1 1
1 -1 1
-1 1 1
1 1 1
fxcand =
-1 -1 -1 -1
-1 -1 -1 -1
1 1 1 1
1 1 1 1
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
-1 -1 -1 -1
-1 -1 -1 -1
1 1 1 1
1 1 1 1
Графическое представление начального множества xcand значений 3-х факторов и полной квадратической модели.
>> nfactors=3;
>> model='quadratic';
>> xcand = candgen(nfactors,model)
xcand =
-1 -1 -1
0 -1 -1
1 -1 -1
-1 0 -1
0 0 -1
1 0 -1
-1 1 -1
0 1 -1
1 1 -1
-1 -1 0
0 -1 0
1 -1 0
-1 0 0
0 0 0
1 0 0
-1 1 0
0 1 0
1 1 0
-1 -1 1
0 -1 1
1 -1 1
-1 0 1
0 0 1
1 0 1
-1 1 1
0 1 1
1 1 1
>> x= xcand (:,1);
>> y= xcand (:,2);
>> z= xcand (:,3);
>> plot3(x,y,z,'o')
>> grid on
ccdesign - Центральный композиционный план
Синтаксис
D = ccdesign(nfactors)
D = ccdesign(nfactors,'pname1',pvalue1,'pname2',pvalue2,...)
[D,blk] = ccdesign(...)
Описание
D = ccdesign(nfactors) функция предназначена для генерации матрицы D центрального композиционного плана для nfactors факторов. Размерность матрицы плана эксперимента D равна nfactors x nfactors. Количество опытов в матрице равно числу факторов. Значения факторов нормализованы таким образом, чтобы вершины куба плана были равны -1 и 1.
[D,blk] = ccdesign(nfactors) функция возвращает вектор номеров блоков blk опытов в плане эксперимента. Блоки позволяют сгруппировать опыты таким образом, чтобы минимизировать влияние изменений внешних условий на значения оцениваемых параметров.
[...] = ccdesign(nfactors,'pname1',pvalue1,'pname2',pvalue2,...) такой вариант синтаксиса позволяет задать следующие дополнительные параметры 'pname' и их значения pvalue:
|
'center' |
Число центральных точек в плане: |
|
|
Целое число |
Определяет число центральных точек в плане |
|
|
'uniform' |
Число центральных точек выбирается для обеспечения равной точности в области проведения эксперимента |
|
|
'orthogonal' |
Число центральных точек выбирается для обеспечения ортогональности плана. Принимается как значение по умолчанию. |
|
|
'fraction' |
Вид дробной реплики от полного факторного плана. Задается в виде степени 1/2. Например: |
|
|
0 |
Полный план |
|
|
1 |
1/2 реплика |
|
|
2 |
1/4 реплика |
|
|
'type' |
Вид центрального композиционного плана. Возможные значения 'inscribed', 'circumscribed', 'faced'. |
|
|
'blocksize' |
Максимальное количество точек в блоке плана |
|
Дополнительные аргументы задаются в виде пары: 'название параметра', значение параметра.
Примеры использования функции генерации матрицы центрального композиционного плана
Генерация матрицы центрального композиционного плана для 3 факторов
>> D = ccdesign(3)
D =
-1.0000 -1.0000 -1.0000
-1.0000 -1.0000 1.0000
-1.0000 1.0000 -1.0000
-1.0000 1.0000 1.0000
1.0000 -1.0000 -1.0000
1.0000 -1.0000 1.0000
1.0000 1.0000 -1.0000
1.0000 1.0000 1.0000
-1.6818 0 0
1.6818 0 0
0 -1.6818 0
0 1.6818 0
0 0 -1.6818
0 0 1.6818
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
Генерация матрицы центрального композиционного плана для 5 факторов разделенного на блоки
>> [D,blk] = ccdesign(5)
|
D= |
blk= |
|
-1 -1 -1 -1 1 -1 -1 -1 1 -1 -1 -1 1 -1 -1 -1 -1 1 1 1 -1 1 -1 -1 -1 -1 1 -1 1 1 -1 1 1 -1 1 -1 1 1 1 -1 1 -1 -1 -1 -1 1 -1 -1 1 1 1 -1 1 -1 1 1 -1 1 1 -1 1 1 -1 -1 1 1 1 -1 1 -1 1 1 1 -1 -1 1 1 1 1 1 -2 0 0 0 0 2 0 0 0 0 0 -2 0 0 0 0 2 0 0 0 0 0 -2 0 0 0 0 2 0 0 0 0 0 -2 0 0 0 0 2 0 0 0 0 0 -2 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 2 2 2 2 2 |
Генерация матрицы 1/2 дробной реплики центрального композиционного плана для 5 факторов разделенного на блоки с числом центральных точек в плане равном 7. Максимальное количество точек в блоке плана - 20.
>> [D,blk] = ccdesign(5, 'center', 7, 'fraction', 1, 'blocksize', 20)
D =
-1 -1 -1 -1 1
-1 -1 -1 1 -1
-1 -1 1 -1 -1
-1 -1 1 1 1
-1 1 -1 -1 -1
-1 1 -1 1 1
-1 1 1 -1 1
-1 1 1 1 -1
1 -1 -1 -1 -1
1 -1 -1 1 1
1 -1 1 -1 1
1 -1 1 1 -1
1 1 -1 -1 1
1 1 -1 1 -1
1 1 1 -1 -1
1 1 1 1 1
-2 0 0 0 0
2 0 0 0 0
0 -2 0 0 0
0 2 0 0 0
0 0 -2 0 0
0 0 2 0 0
0 0 0 -2 0
0 0 0 2 0
0 0 0 0 -2
0 0 0 0 2
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
blk =
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
1
1
1
2
2
2
2
Генерация матрицы 1/2 дробной реплики центрального композиционного плана для 5 факторов разделенного на блоки с числом центральных точек расположенных с целью обеспечения равной точности в области проведения эксперимента. Вид центрального композиционного плана - 'inscribed'.
>> [D,blk] = ccdesign(5, 'center', 'uniform', 'fraction', 1, 'type', 'inscribed')
D =
-0.5000 -0.5000 -0.5000 -0.5000 0.5000
-0.5000 -0.5000 -0.5000 0.5000 -0.5000
-0.5000 -0.5000 0.5000 -0.5000 -0.5000
-0.5000 -0.5000 0.5000 0.5000 0.5000
-0.5000 0.5000 -0.5000 -0.5000 -0.5000
-0.5000 0.5000 -0.5000 0.5000 0.5000
-0.5000 0.5000 0.5000 -0.5000 0.5000
-0.5000 0.5000 0.5000 0.5000 -0.5000
0.5000 -0.5000 -0.5000 -0.5000 -0.5000
0.5000 -0.5000 -0.5000 0.5000 0.5000
0.5000 -0.5000 0.5000 -0.5000 0.5000
0.5000 -0.5000 0.5000 0.5000 -0.5000
0.5000 0.5000 -0.5000 -0.5000 0.5000
0.5000 0.5000 -0.5000 0.5000 -0.5000
0.5000 0.5000 0.5000 -0.5000 -0.5000
0.5000 0.5000 0.5000 0.5000 0.5000
-1.0000 0 0 0 0
1.0000 0 0 0 0
0 -1.0000 0 0 0
0 1.0000 0 0 0
0 0 -1.0000 0 0
0 0 1.0000 0 0
0 0 0 -1.0000 0
0 0 0 1.0000 0
0 0 0 0 -1.0000
0 0 0 0 1.0000
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
blk =
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
1
1
1
2
2
2
Графическое представление 3-х видов центрального композиционного плана для 3 факторов
>> nfactors=3;
>> D = ccdesign(nfactors, 'type', 'inscribed');
>> x= D(:,1);
>> y= D (:,2);
>> z= D (:,3);
>> subplot(1,3,1)
>> plot3(x,y,z,'o')
>> grid on
>> D1 = ccdesign(nfactors, 'type', 'circumscribed');
>> x1= D1(:,1);
>> y1= D1 (:,2);
>> z1= D1 (:,3);
>> subplot(1,3,2)
>> plot3(x1,y1,z1,'dr')
>> grid on
>> D2 = ccdesign(nfactors, 'type', 'faced');
>> x2= D2(:,1);
>> y2= D2 (:,2);
>> z2= D2 (:,3);
>> subplot(1,3,3)
>> plot3(x2,y2,z2,'+r')
>> grid on
cordexch - Функция для определения точного D-оптимального плана эксперимента на основе алгорима обмена координатами
Синтаксис
settings = cordexch(nfactors,nruns)
[settings,X] = cordexch(nfactors,nruns)
[settings,X] = cordexch(nfactors,nruns,'model')
[settings,X] = cordexch(...,'param1',value1,'param2',value2,...)
Описание
settings = cordexch(nfactors,nruns) функция позволяет получить матрицу значений факторов settings D-оптимального плана на основе алгоритма изменения координат для линейной регрессионной модели. Количество факторов задается входным аргументом nfactors, число опытов в плане - nruns. Размерность матрицы settings составляет nruns строк, nfactors столбцов.
[settings,X] = cordexch(nfactors,nruns) в отличии от первого варианта синтаксиса функция возвращает матрицу D-оптимального плана X.
[settings,X] = cordexch(nfactors,nruns,'model') функция позволяет получить матрицу значений факторов settings и матрицу D-оптимального плана эксперимента Х на основе алгоритма изменения координат для заданного числа факторов nfactors, числа опытов nruns и вида уравнения регрессии 'model'. Возможны следующие виды модели регрессии
|
Значение 'model' |
Вид математической модели |
|
'linear' |
Линейная модель с постоянным членом. Значение по умолчанию. |
|
'interaction' |
Линейная модель с постоянным членом и эффектами взаимодействия. |
|
'quadratic' |
Полная квадратическая модель, включающая линейные, квадратические эффекты, эффекты взаимодействий, постоянный член. |
|
'purequadratic' |
Неполная квадратическая модель, включающая линейные, квадратические эффекты, постоянный член. |
Кроме строкового значения входной аргумент model может быть задан как вектор или матрица аналогично такому же аргументу функции x2fx. Функция x2fx позволяет выполнить преобразование матрицы значений факторов Х в матрицу плана эксперимента D. В случае, если X и model заданы как векторы, то матрица плана эксперимента формируется по правилу: каждый столбец D является последовательным возведением Х в степень элемента вектора model. Размерность матрицы D равна n?m, где n - число элементов вектора Х, m - число элементов вектора model. Т.е., вектор model является списком степеней полинома регрессионной модели для одного фактора Х. Если X и model заданы как матрицы, то столбец матрицы D формируются по формуле:
D(i,j)=prod(Х(i,:).^model(j,:)),
т.е., ij-й элемент матрицы D является произведением элементов i-й строки матрицы Х возведенных последовательно в степени j-й строки матрицы model. Таким образом, количество столбцов model должно быть равно числу столбцов матрицы Х.
[settings,X] = cordexch(...,'param1',value1,'param2',value2,...) дополнительные входные аргументы по отношению к предыдущим вариантам синтаксиса позволяют:
|
'display' |
Вывод значения счетчика итераций. Возможные значения 'display': 'on' - вывод в командное окно, 'off' - отмена отображения. Значение по умолчанию 'on'. |
|
'init' |
Начальная матрица значений факторов с размерностью nruns x nfactors. По умолчанию начальное множество точек в факторном пространстве выбирается случайным образом. |
|
'maxiter' |
Максимальное число итераций. Значение по умолчанию - 10. |
Примечание. Функция cordexch выполняет поиск D-оптимального плана на основе алгоритма перестановки координат. На первом этапе генерируется начальный план эксперимента. На втором этапе выполняется изменение каждой координаты точек плана с целью минимизации дисперсии коэффициентов уравнения регрессии.
Примеры использования функции генерации матрицы D-оптимального плана на основе алгоритма изменения координат
Генерация матрицы значений факторов D-оптимального плана для трех факторов и 6 опытов. Принимается по умолчанию линейная модель.
>> nfactors=3;
>> nruns=6;
>> settings = cordexch(nfactors,nruns)
settings =
1 -1 -1
1 1 -1
-1 1 -1
1 1 1
-1 -1 1
-1 -1 -1
Генерация матрицы значений факторов и матрицы D-оптимального плана для трех факторов,
12 опытов и полной квадратической модели.
>> nfactors=3;
>> nruns=12;
>> [settings,X] = cordexch(nfactors,nruns,'quadratic')
settings =
-1 1 -1
1 -1 -1
-1 -1 1
-1 0 0
0 0 -1
-1 1 1
-1 -1 -1
1 1 -1
1 -1 1
1 1 1
0 1 1
0 -1 0
X =
1 -1 1 -1 -1 1 -1 1 1 1
1 1 -1 -1 -1 -1 1 1 1 1
1 -1 -1 1 1 -1 -1 1 1 1
1 -1 0 0 0 0 0 1 0 0
1 0 0 -1 0 0 0 0 0 1
1 -1 1 1 -1 -1 1 1 1 1
1 -1 -1 -1 1 1 1 1 1 1
1 1 1 -1 1 -1 -1 1 1 1
1 1 -1 1 -1 1 -1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 0 1 1 0 0 1 0 1 1
1 0 -1 0 0 0 0 0 1 0
Генерация матрицы значений факторов и матрицы D-оптимального плана для 3 факторов,
20 опытов и регрессионной модели заданной в виде матрицы model.
>> nfactors=3;
>> nruns=20;
>> model=[ 0 1 2; 1 2 3; 0 1 2 ; 1 2 3]
model =
0 1 2
1 2 3
0 1 2
1 2 3
>> [settings,X] = cordexch(nfactors,nruns,model)
settings =
1 1 1
1 1 -1
-1 -1 1
1 -1 1
1 -1 -1
-1 1 -1
1 1 -1
-1 -1 1
-1 -1 -1
-1 1 1
1 -1 -1
1 -1 1
1 -1 -1
1 1 1
-1 1 -1
-1 -1 -1
1 1 1
1 -1 1
1 1 1
-1 -1 1
X =
1 1 1 1
1 -1 1 -1
-1 -1 -1 -1
-1 1 -1 1
-1 -1 -1 -1
1 1 1 1
1 -1 1 -1
-1 -1 -1 -1
-1 1 -1 1
1 -1 1 -1
-1 -1 -1 -1
-1 1 -1 1
-1 -1 -1 -1
1 1 1 1
1 1 1 1
-1 1 -1 1
1 1 1 1
-1 1 -1 1
1 1 1 1
-1 -1 -1 -1
Генерация матриц значений факторов и D-оптимального плана для трех факторов, 12 опытов,
полной квадратической модели. В качестве дополнительного входного аргумента задается матрица
начального приближения А.
>> nfactors=3;
>> nruns=12;
>> A=[0 0 0; 1 0 0; -1 0 0; 0 1 0; 1 1 -1; -1 0 -1; 1 0 0 ; 0 0 1; -1 1 -1; 1 0 -1; 1 1 1; 0 -1 0]
A =
0 0 0
1 0 0
-1 0 0
0 1 0
1 1 -1
-1 0 -1
1 0 0
0 0 1
-1 1 -1
1 0 -1
1 1 1
0 -1 0
>> [settings,X] = cordexch(nfactors,nruns,'quadratic','init',A)
settings =
0 0 -1
1 -1 -1
-1 -1 1
-1 1 1
1 1 -1
-1 -1 -1
-1 0 0
1 -1 1
-1 1 -1
1 0 0
1 1 1
0 -1 0
X =
1 0 0 -1 0 0 0 0 0 1
1 1 -1 -1 -1 -1 1 1 1 1
1 -1 -1 1 1 -1 -1 1 1 1
1 -1 1 1 -1 -1 1 1 1 1
1 1 1 -1 1 -1 -1 1 1 1
1 -1 -1 -1 1 1 1 1 1 1
1 -1 0 0 0 0 0 1 0 0
1 1 -1 1 -1 1 -1 1 1 1
1 -1 1 -1 -1 1 -1 1 1 1
1 1 0 0 0 0 0 1 0 0
1 1 1 1 1 1 1 1 1 1
1 0 -1 0 0 0 0 0 1 0
Графическое представление матрицы значений факторов D-оптимального плана для трех факторов,
12 опытов и полной квадратической модели
>> nfactors=3;
>> nruns=12;
>> settings = cordexch(nfactors,nruns,'quadratic')
>> x= settings (:,1);
>> y= settings (:,2);
>> z= settings (:,3);
>> plot3(x,y,z,'o')
>> grid on
daugment - Определение матрица плана дополняющую матрицу заданного плана до D-оптимального
Синтаксис
settings = daugment(startdes,nruns)
[settings,X] = daugment(startdes,nruns)
[settings,X] = daugment(startdes,nruns,'model')
[settings, X] = daugment(...,'param1',value1,'param2',value2,...)
Описание
settings = daugment(startdes,nruns) функция предназначена для дополнения nruns опытов к входной матрице startdes с целью получения D-оптимальной матрицы значений факторов плана эксперимента settings. Функция основана на алгоритме изменения координат.
[settings,X] = daugment(startdes,nruns) в отличии от первого варианта синтаксиса функция возвращает матрицу X D-оптимального плана эксперимента.
[settings,X] = daugment(startdes,nruns,'model') функция позволяет получить матрицу значений факторов settings и матрицу D-оптимального плана эксперимента Х на основе алгоритма изменения координат для исходной матрицы значений факторов startdes, заданного числа опытов nruns и вида уравнения регрессии 'model'. Возможны следующие модели регрессии
|
Значение 'model' |
Вид математической модели |
|
'linear' |
Линейная модель с постоянным членом. Значение по умолчанию. |
|
'interaction' |
Линейная модель с постоянным членом и эффектами взаимодействия. |
|
'quadratic' |
Полная квадратическая модель, включающая линейные, квадратические эффекты, эффекты взаимодействий, постоянный член. |
|
'purequadratic' |
Неполная квадратическая модель, включающая линейные, квадратические эффекты, постоянный член. |
Кроме строкового значения входной аргумент model может быть задан как вектор или матрица согласно такому же аргументу функции x2fx. Функция x2fx позволяет выполнить преобразование матрицы значений факторов Х в матрицу плана эксперимента D. В случае, если X и model заданы как векторы, то матрица плана эксперимента формируется по правилу: каждый столбец D является последовательным возведением Х в степень элемента вектора model. Размерность матрицы D равна n?m, где n - число элементов вектора Х, m - число элементов вектора model. Т.е., вектор model является списком степеней полинома регрессионной модели для одного фактора Х. Если X и model заданы как матрицы, то столбец матрицы D формируются по формуле:
D(i,j)=prod(Х(i,:).^model(j,:)),
т.е., ij-й элемент матрицы D является произведением элементов i-й строки матрицы Х возведенных последовательно в степени j-й строки матрицы model. Таким образом, количество столбцов model должно быть равно числу столбцов матрицы Х.
[settings, X] = daugment(...,'param1',value1,'param2',value2,...) дополнительные входные аргументы по отношению к предыдущим вариантам синтаксиса позволяют:
|
'display' |
Вывод значения счетчика итераций. Возможные значения 'display': 'on' - вывод в командное окно, 'off' - отмена отображения. Значение по умолчанию 'on'. |
|
'init' |
Начальная матрица значений факторов с размерностью nruns x nfactors. По умолчанию предусматривается формирование начальной матрицы значений факторов случайным образом. |
|
'maxiter' |
Максимальное число итераций. Значение по умолчанию - 10. |
Примеры использования функции дополнения матрицы значений факторов до D-оптимального плана эксперимента
Дополнение матрицы значений факторов полного факторного эксперимента 22 до D-оптимальной матрицы значений факторов. Модель регрессии принимается по умолчанию линейной. Количество добавляемых опытов 5.
>> nruns=5;
>> startdes = [-1 -1; 1 -1; -1 1; 1 1]
startdes =
-1 -1
1 -1
-1 1
1 1
>> settings = daugment(startdes,nruns)
settings =
-1 -1
1 -1
-1 1
1 1
1 -1
-1 -1
-1 1
1 1
-1 -1
Дополнение матрицы значений факторов полного факторного эксперимента 22 до D-оптимальной матрицы значений факторов и матрицы плана эксперимента для полной квадратической модели. Количество добавляемых опытов 5.
>> nruns=5;
>> startdes = [-1 -1; 1 -1; -1 1; 1 1]
startdes =
-1 -1
1 -1
-1 1
1 1
>> [settings,X] = daugment(startdes,nruns,'quadratic')
settings =
-1 -1
1 -1
-1 1
1 1
-1 0
1 0
0 1
0 -1
0 0
X =
1 -1 -1 1 1 1
1 1 -1 -1 1 1
1 -1 1 -1 1 1
1 1 1 1 1 1
1 -1 0 0 1 0
1 1 0 0 1 0
1 0 1 0 0 1
1 0 -1 0 0 1
1 0 0 0 0 0
Дополнение матрицы значений факторов полного факторного эксперимента 22 до D-оптимальной матрицы значений факторов и матрицы плана эксперимента. Количество добавляемых опытов 5. Модель регрессии задается в виде матрицы model.
>> nruns=5;
>> startdes = [-1 -1; 1 -1; -1 1; 1 1]
startdes =
-1 -1
1 -1
-1 1
1 1
>> model=[0 1; 1 2; 2 3]
model =
0 1
1 2
2 3
>> [settings,X] = daugment(startdes,nruns,model)
settings =
-1.0000 -1.0000
1.0000 -1.0000
-1.0000 1.0000
1.0000 1.0000
-1.0000 1.0000
0.0184 1.0000
-0.3333 -1.0000
-0.3333 1.0000
-1.0000 -1.0000
X =
-1.0000 -1.0000 -1.0000
-1.0000 1.0000 -1.0000
1.0000 -1.0000 1.0000
1.0000 1.0000 1.0000
1.0000 -1.0000 1.0000
1.0000 0.0184 0.0003
-1.0000 -0.3333 -0.1111
1.0000 -0.3333 0.1111
-1.0000 -1.0000 -1.0000
Дополнение матрицы значений факторов полного факторного эксперимента 22 до D-оптимальной матрицы значений факторов и матрицы плана эксперимента для полной квадратической модели. Количество добавляемых опытов 5. В качестве дополнительного входного аргумента задается матрица начального приближения А.
>> nruns=5;
>> startdes = [-1 -1; 1 -1; -1 1; 1 1]
startdes =
-1 -1
1 -1
-1 1
1 1
>> A=[0 0; 0 1; 1 0; 1 1; -1 1]
A =
0 0
0 1
1 0
1 1
-1 1
>> [settings,X] = daugment(startdes,nruns,'quadratic','init',A)
settings =
-1 -1
1 -1
-1 1
1 1
0 0
0 -1
1 0
0 1
-1 0
X =
1 -1 -1 1 1 1
1 1 -1 -1 1 1
1 -1 1 -1 1 1
1 1 1 1 1 1
1 0 0 0 0 0
1 0 -1 0 0 1
1 1 0 0 1 0
1 0 1 0 0 1
1 -1 0 0 1 0
Графическое представление матрицы значений факторов полного факторного эксперимента 23 Х и дополненной до D-оптимальной матрицы значений факторов settings. Количество добавляемых опытов 5.
>> startdes = ff2n(3)
startdes =
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
>> nruns=5;
>> settings = daugment(startdes,nruns)
settings =
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
-1 -1 1
1 -1 -1
-1 1 -1
-1 -1 -1
-1 -1 1
>> x= X (:,1);
>> y= X (:,2);
>> z= X (:,3);
>> subplot(1,2,1)
>> plot3(x,y,z,'o')
>> grid on
>> x1= settings (:,1);
>> y1= settings (:,2);
>> z1= settings (:,3);
>> subplot(1,2,2)
>> plot3(x1,y1,z1,'dr')
>> grid on
dcovary - Функция для построения D-оптимального блочного плана
Синтаксис
settings = dcovary(nfactors,covariates)
[settings,X] = dcovary(nfactors,covariates)
[settings,X] = dcovary(nfactors,covariates,'model')
[settings,X] = dcovary(...,'param1',value1,'param2',value2,...)
Описание
settings = dcovary(nfactors,covariates) функция позволяет получить матрицу значений факторов settings D-оптимального плана разделенного на блоки covariates для заданного числа факторов nfactors. Количество опытов в плане эксперимента задается числом строк в матрице covariates. Матрица значений факторов settings формируется последовательно из двух матриц: матрицы значений факторов D-оптимального плана и матрицы, кодирующей блоки плана. Размерность матрицы settings равна nxm, где n - количество строк матрицы covariates, m=nfactors+k, где k - количество столбцов матрицы settings. Функция основана на алгоритме изменения координат.
[settings,X] = dcovary(nfactors,covariates) в отличии от первого варианта синтаксиса функция возвращает матрицу D-оптимального плана X.
[settings,X] = dcovary(nfactors,covariates,'model') функция позволяет получить матрицу значений факторов settings и матрицу D-оптимального плана эксперимента Х на основе на основе матрицы covariates, задающей блоки и количество опытов, заданного числа факторов nfactors, и вида уравнения регрессии 'model'. Возможны следующие модели регрессии
|
Значение 'model' |
Вид математической модели |
|
'linear' |
Линейная модель с постоянным членом. Значение по умолчанию. |
|
'interaction' |
Линейная модель с постоянным членом и эффектами взаимодействия. |
|
'quadratic' |
Полная квадратическая модель, включающая линейные, квадратические эффекты, эффекты взаимодействий, постоянный член. |
|
'purequadratic' |
Неполная квадратическая модель, включающая линейные, квадратические эффекты, постоянный член. |
Кроме строкового значения входной аргумент model может быть задан как вектор или матрица согласно такому же аргументу функции x2fx. Функция x2fx позволяет выполнить преобразование матрицы значений факторов Х в матрицу плана эксперимента D. В случае, если X и model заданы как векторы, то матрица плана эксперимента формируется по правилу: каждый столбец D является последовательным возведением Х в степень элемента вектора model. Размерность матрицы D равна nxm, где n - число элементов вектора Х, m - число элементов вектора model. Т.е., вектор model является списком степеней полинома регрессионной модели для одного фактора Х. Если X и model заданы как матрицы, то столбец матрицы D формируются по формуле:
D(i,j)=prod(Х(i,:).^model(j,:)),
т.е., ij-й элемент матрицы D является произведением элементов i-й строки матрицы Х возведенных последовательно в степени j-й строки матрицы model. Таким образом, количество столбцов model должно быть равно числу столбцов матрицы Х.
[settings, X] = dcovary(...,'param1',value1,'param2',value2,...) дополнительные входные аргументы по отношению к предыдущим вариантам синтаксиса позволяют:
|
'display' |
Вывод значения счетчика итераций. Возможные значения 'display': 'on' - вывод в командное окно, 'off' - отмена отображения. Значение по умолчанию 'on'. |
|
'init' |
Начальная матрица значений факторов с размерностью nruns x nfactors. По умолчанию предусматривается формирование начальной матрицы значений факторов случайным образом. |
|
'maxiter' |
Максимальное число итераций. Значение по умолчанию - 10. |
Примечание. Функция dcovary выполняет поиск D-оптимального плана на основе алгоритма перестановки координат. На первом этапе генерируется начальный план эксперимента, содержащий постоянные кодовые значения, разделяющие матрицу плана на блоки, и переменные значения - значения уровней факторов. На втором этапе выполняется изменение для каждой переменной координат точек плана с целью минимизации дисперсии коэффициентов уравнения регрессии.
Примеры использования функции генерации D-оптимального блочного плана
Генерация матрицы значений факторов D-оптимального плана для 3 факторов разделенного на 2 блока по 4 опыта в каждом. Деление на блоки задается посредством векторной переменной covariates: "-1" кодирует первый блок, "1" кодирует второй блок. Четвертый столбец в матрице settings является блоковой переменной.
>> nfactors=3;
>> covariates=[-1 -1 -1 -1 1 1 1 1]'
covariates =
-1
-1
-1
-1
1
1
1
1
>> settings = dcovary(nfactors,covariates)
settings =
1 -1 1 -1
1 1 -1 -1
-1 -1 -1 -1
-1 1 1 -1
1 -1 1 1
-1 1 1 1
-1 -1 -1 1
1 1 -1 1
Генерация матрицы значений факторов и матрицы D-оптимального плана для 4 факторов разделенного
на 3 блока по 3 опыта в каждом. Деление на блоки задается посредством векторной переменной covariates.
>> nfactors=4;
>> covariates=[-1 -1 -1 1 1 1 2 2 2]'
covariates =
-1
-1
-1
1
1
1
2
2
2
>> [settings,X] = dcovary(nfactors,covariates)
settings =
1 1 -1 -1 -1
-1 1 1 -1 -1
-1 -1 -1 1 -1
1 -1 1 1 1
-1 1 1 1 1
-1 1 -1 -1 1
-1 -1 -1 -1 2
1 1 -1 1 2
1 -1 1 -1 2
X =
1 1 1 -1 -1 -1
1 -1 1 1 -1 -1
1 -1 -1 -1 1 -1
1 1 -1 1 1 1
1 -1 1 1 1 1
1 -1 1 -1 -1 1
1 -1 -1 -1 -1 2
1 1 1 -1 1 2
1 1 -1 1 -1 2
Генерация матрицы значений факторов и матрицы D-оптимального плана для 2 факторов разделенного
на 4 блока по 2 опыта в каждом. Деление на блоки задается посредством матрицы covariates.
Матрица covariates формируется с помощью функции dummyvar преобразованием вектора [1 1 2 2 3 3 4 4].
В качестве уравнения регрессии принимается линейная модель.
>> covariates = dummyvar([1 1 2 2 3 3 4 4])
covariates =
1 0 0 0
1 0 0 0
0 1 0 0
0 1 0 0
0 0 1 0
0 0 1 0
0 0 0 1
0 0 0 1
>> nfactors=2;
>> [settings,X] = dcovary(nfactors,covariates(:,1:3),'linear')
settings =
-1 1 1 0 0
1 -1 1 0 0
1 1 0 1 0
-1 -1 0 1 0
1 -1 0 0 1
-1 1 0 0 1
1 1 0 0 0
-1 -1 0 0 0
X =
1 -1 1 1 0 0
1 1 -1 1 0 0
1 1 1 0 1 0
1 -1 -1 0 1 0
1 1 -1 0 0 1
1 -1 1 0 0 1
1 1 1 0 0 0
1 -1 -1 0 0 0
Генерация матрицы значений факторов и матрицы D-оптимального плана для 2 факторов разделенного
на 4 блока по 2 опыта в каждом. Деление на блоки задается посредством вектора covariates.
Модель регрессии задается как матрица model.
>> covariates=[1 1 2 2 3 3 4 4]';
>> nfactors=2;
>> model=[0 1 2; 0 1 2; 0 1 2]
model =
0 1 2
0 1 2
0 1 2
>> [settings,X] = dcovary(nfactors,covariates, model)
settings =
-0.9852 -1.0000 1.0000
0.5776 -1.0000 1.0000
-0.9644 -1.0000 2.0000
0.7559 -1.0000 2.0000
-0.2949 -1.0000 3.0000
0.4443 -1.0000 3.0000
0.9369 -1.0000 4.0000
-0.6887 -1.0000 4.0000
X =
-1 -1 -1
-1 -1 -1
-4 -4 -4
-4 -4 -4
-9 -9 -9
-9 -9 -9
-16 -16 -16
-16 -16 -16
Генерация матрицы значений факторов и матрицы D-оптимального плана для 3 факторов разделенного
на 3 блока по 3 опыта в каждом. Деление на блоки задает вектор covariates.
В качестве дрполнительного параметра используется матрица начального приближения А.
>> nfactors=3;
>> covariates=[-1 -1 -1 1 1 1 2 2 2]';
>> A=[ 0 0 0; 1 0 0; 0 1 0; -1 0 0; -1 -1 0; 0 0 -1; 1 -1 1; -1 -1 1; 1 -1 -1]
A =
0 0 0
1 0 0
0 1 0
-1 0 0
-1 -1 0
0 0 -1
1 -1 1
-1 -1 1
1 -1 -1
>> [settings,X] = dcovary(nfactors,covariates,'purequadratic')
settings =
1 -1 -1 -1
-1 0 1 -1
0 1 0 -1
-1 -1 1 1
1 0 0 1
0 0 -1 1
-1 1 -1 2
0 -1 0 2
1 1 1 2
X =
1 1 -1 -1 -1 1 1 1 1
1 -1 0 1 -1 1 0 1 1
1 0 1 0 -1 0 1 0 1
1 -1 -1 1 1 1 1 1 1
1 1 0 0 1 1 0 0 1
1 0 0 -1 1 0 0 1 1
1 -1 1 -1 2 1 1 1 4
1 0 -1 0 2 0 1 0 4
1 1 1 1 2 1 1 1 4
Графическое представление матрицы D-оптимального плана эксперимента для 3 факторов, разделенного
на 2 блока по 5 опытов в каждом. Матрица D-оптимального плана рассчитывается для неполной
квадратической модели.
>> nfactors=3;
>> covariates=[0 0 0 0 0 1 1 1 1 1]';
>> settings = dcovary(nfactors,covariates,'purequadratic')
settings =
-1 1 0 0
-1 0 1 0
1 -1 1 0
1 1 -1 0
0 0 -1 0
0 1 1 1
1 0 0 1
0 -1 0 1
-1 1 -1 1
-1 -1 -1 1
Первый блок
>> x= settings (1:5,1);
>> y= settings (1:5,2);
>> z= settings (1:5,3);
>> subplot(1,3,1)
>> plot3(x,y,z,'o')
>> grid on
Второй блок
>> x1= settings (6:10,1);
>> y1= settings (6:10,2);
>> z1= settings (6:10,3);
>> subplot(1,3,2)
>> plot3(x1,y1,z1,'dr')
>> grid on
Общий график
>> subplot(1,3,3)
>> plot3(x,y,z,'o',x1,y1,z1,'dr')
>> grid on
ff2n - Определение плана полного факторного эксперимента для факторов имеющих 2 уровня
Синтаксис
X = ff2n(n)
Описание
X = ff2n(n) функция позволяет получить матрицу плана Х полного факторного эксперимента при условии, что все факторы входящие в план изменяются на двух уровнях. Входной аргумент n - количество факторов в эксперименте. Размерность матрицы плана эксперимента равна 2nxn, где 2n - число строк или число опытов в эксперименте, n - число столбцов. Элементы матрицы плана эксперимента выражаются в кодированной форме и равны 0 или 1. 0 соответствует минимальному значению фактора, 1 - максимальному значению фактора. Матрица плана эксперимента Х не рандомизирована и представляет собой последовательный перебор всех возможных комбинаций значений факторов.
Примеры использования функции генерации полного факторного эксперимента для факторов, изменяющихся на 2-х уровнях
Матрица плана полного 5-ти факторного эксперимента
>> n=5
n =
5
>> X = ff2n(n)
X =
0 0 0 0 0
0 0 0 0 1
0 0 0 1 0
0 0 0 1 1
0 0 1 0 0
0 0 1 0 1
0 0 1 1 0
0 0 1 1 1
0 1 0 0 0
0 1 0 0 1
0 1 0 1 0
0 1 0 1 1
0 1 1 0 0
0 1 1 0 1
0 1 1 1 0
0 1 1 1 1
1 0 0 0 0
1 0 0 0 1
1 0 0 1 0
1 0 0 1 1
1 0 1 0 0
1 0 1 0 1
1 0 1 1 0
1 0 1 1 1
1 1 0 0 0
1 1 0 0 1
1 1 0 1 0
1 1 0 1 1
1 1 1 0 0
1 1 1 0 1
1 1 1 1 0
1 1 1 1 1
Графически матрицу планирования полного факторного эксперимента для трех факторов
можно представить следующим образом
>> n=3;
>> X = ff2n(n)
X =
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
>> x= X (:,1);
>> y= X (:,2);
>> z= X (:,3);
>> plot3(x,y,z,'o')
>> grid on
fracfact - Функция для формирования двухуровнего дробного факторного плана
Синтаксис
x = fracfact('gen')
[x,conf] = fracfact('gen')
Описание
x = fracfact('gen') служит для генерации матрицы x плана дробного факторного эксперимента согласно генератору 'gen'. Значения факторов в матрице плана эксперимента х равны 1 и -1. 1 соответствует максимальному уровню фактора, -1 - минимальному уровню. Генератор 'gen' является строковой переменной, состоящей из подстрок разделенных пробелами. Подстрока может состоять из одной и более букв латинского алфавита. В первую очередь задаются односимвольные подстроки, кодирующие факторы для матрицы полного факторного эксперимента. Эта матрица является основой дробного факторного плана. Правила определения значений остальных факторов в матрице дробного плана задаются в виде сочетаний символов, кодирующих факторы полного факторного эксперимента. Для этих факторов значения определяются как произведения значений кодированных переменных, соответствующих первой группе факторов. Например, для генератора 'gen'='a b ab' первые два фактора: a и b, образуют матрицу полного факторного плана вида:
>> x = ff2n(2)
x =
0 0
0 1
1 0
1 1
Подстрока ab определяет значение третьего фактора как построчное произведение a и b.
>> x = fracfact('a b ab')
x =
-1 -1 1
-1 1 -1
1 -1 -1
1 1 1
Для факторов второй группы комбинация символов в подстроке определяют вид смешивания их главных эффектов. Т.е., в предыдущем примере главный эффект третьего фактора β3 будет смешан с парным эффектом первых двух факторов β12 :
β3 -> β3 + β12
Матрица дробного факторного плана x является частью матрицы полного факторного плана эксперимента образованного всеми факторами. Число строк матрицы плана x равно 2n, где n - количество односимвольных подстрок в генераторе. Количество столбцов в матрице плана должно быть равно числу подстрок в генераторе. [x,conf] = fracfact('gen') этот вариант синтаксиса функции возвращает матрицу conf показывающую способ смешивания главных эффектов факторов и их парных взаимодействий.
Примеры использования функции генерации матрицы дробного факторного эксперимента
Пример 1
Целью эксперимента является оценка величин главных (линейных) эффектов 4 факторов на функцию отклика при проведении восьми опытов. Каждый опыт проводится без повторений.
Проведение полного факторного эксперимента потребует 42=16 опытов. Однако, если на основании априорных данных предположить незначимость тройных взаимодействий, то можно оценить величины главных эффектов четырех факторов в восьми опытах.
Матрица планирования дробного факторного эксперимента x в этом случае примет вид
>> [x,conf] = fracfact('a b c abc')
x =
-1 -1 -1 -1
-1 -1 1 1
-1 1 -1 1
-1 1 1 -1
1 -1 -1 1
1 -1 1 -1
1 1 -1 -1
1 1 1 1
conf =
'Term' 'Generator' 'Confounding'
'X1' 'a' 'X1'
'X2' 'b' 'X2'
'X3' 'c' 'X3'
'X4' 'abc' 'X4'
'X1*X2' 'ab' 'X1*X2 + X3*X4'
'X1*X3' 'ac' 'X1*X3 + X2*X4'
'X1*X4' 'bc' 'X1*X4 + X2*X3'
'X2*X3' 'bc' 'X1*X4 + X2*X3'
'X2*X4' 'ac' 'X1*X3 + X2*X4'
'X3*X4' 'ab' 'X1*X2 + X3*X4'
Первые 3 столбца матрицы х представляют матрицу полного факторного эксперимента для трех факторов a, b, c. Четвертый столбец получен построчным перемножением значений первых трех факторов. Матрица conf показывает, что такое планирование эксперимента позволяет оценить не смешанные главные эффекты для всех четырех факторов. Парные взаимодействия смешаны друг с другом. Например, эффект от парного взаимодействия первого и второго факторов смешан с эффектом парного взаимодействия третьего и четвертого факторов: X1*X2 + X3*X4. Это не позволяет раздельно оценить их эффекты.
В случае, если после проведения указанных восьми опытов выясниться что суммарный эффект от взаимодействия X1*X2+X3*X4 значим, то целесообразно определить какое парное взаимодействие значимо X1*X2 или X3*X4. Для этого дробную реплику из первых восьми опытов можно дополнить второй репликой до полного факторного эксперимента. Матрица второй реплики задается тем же генератором, но с обратным знаком для четвертого фактора:
>> fracfact('a b c -abc')
ans =
-1 -1 -1 1
-1 -1 1 -1
-1 1 -1 -1
-1 1 1 1
1 -1 -1 -1
1 -1 1 1
1 1 -1 1
1 1 1 -1
Пример 2
Необходимо оценить величины линейных эффектов восьми факторов. Поскольку в большинстве случаев парные эффекты взаимодействия больше эффектов взаимодействия высших порядков, то необходимо так составить дробную реплику, чтобы линейные эффекты не были смешаны с ними при минимальном количестве опытов. Поведение полного факторного эксперимента потребовало бы 82=256 опытов. Использование дробной реплики полного факторного эксперимента позволяет при 16 опытах получить оценки главных эффектов 8 факторов не смешанных с парными взаимодействиями. Реплику 16/256 для названных условий можно получить с использованием следующего генератора
>> [x, conf] = fracfact('a b c d abc acd abd bcd')
x =
-1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 1 -1 1 1 1
-1 -1 1 -1 1 1 -1 1
-1 -1 1 1 1 -1 1 -1
-1 1 -1 -1 1 -1 1 1
-1 1 -1 1 1 1 -1 -1
-1 1 1 -1 -1 1 1 -1
-1 1 1 1 -1 -1 -1 1
1 -1 -1 -1 1 1 1 -1
1 -1 -1 1 1 -1 -1 1
1 -1 1 -1 -1 -1 1 1
1 -1 1 1 -1 1 -1 -1
1 1 -1 -1 -1 1 -1 1
1 1 -1 1 -1 -1 1 -1
1 1 1 -1 1 -1 -1 -1
1 1 1 1 1 1 1 1
conf =
Term Generator Confounding
X1 a X1
X2 b X2
X3 c X3
X4 d X4
X5 abc X5
X6 acd X6
X7 abd X7
X8 bcd X8
X1*X2 ab X1*X2 + X3*X5 + X4*X7 + X6*X8
X1*X3 ac X1*X3 + X2*X5 + X4*X6 + X7*X8
X1*X4 ad X1*X4 + X2*X7 + X3*X6 + X5*X8
X1*X5 bc X1*X5 + X2*X3 + X4*X8 + X6*X7
X1*X6 cd X1*X6 + X2*X8 + X3*X4 + X5*X7
X1*X7 bd X1*X7 + X2*X4 + X3*X8 + X5*X6
X1*X8 abcd X1*X8 + X2*X6 + X3*X7 + X4*X5
X2*X3 bc X1*X5 + X2*X3 + X4*X8 + X6*X7
X2*X4 bd X1*X7 + X2*X4 + X3*X8 + X5*X6
X2*X5 ac X1*X3 + X2*X5 + X4*X6 + X7*X8
X2*X6 abcd X1*X8 + X2*X6 + X3*X7 + X4*X5
X2*X7 ad X1*X4 + X2*X7 + X3*X6 + X5*X8
X2*X8 cd X1*X6 + X2*X8 + X3*X4 + X5*X7
X3*X4 cd X1*X6 + X2*X8 + X3*X4 + X5*X7
X3*X5 ab X1*X2 + X3*X5 + X4*X7 + X6*X8
X3*X6 ad X1*X4 + X2*X7 + X3*X6 + X5*X8
X3*X7 abcd X1*X8 + X2*X6 + X3*X7 + X4*X5
X3*X8 bd X1*X7 + X2*X4 + X3*X8 + X5*X6
X4*X5 abcd X1*X8 + X2*X6 + X3*X7 + X4*X5
X4*X6 ac X1*X3 + X2*X5 + X4*X6 + X7*X8
X4*X7 ab X1*X2 + X3*X5 + X4*X7 + X6*X8
X4*X8 bc X1*X5 + X2*X3 + X4*X8 + X6*X7
X5*X6 bd X1*X7 + X2*X4 + X3*X8 + X5*X6
X5*X7 cd X1*X6 + X2*X8 + X3*X4 + X5*X7
X5*X8 ad X1*X4 + X2*X7 + X3*X6 + X5*X8
X6*X7 bc X1*X5 + X2*X3 + X4*X8 + X6*X7
X6*X8 ab X1*X2 + X3*X5 + X4*X7 + X6*X8
X7*X8 ac X1*X3 + X2*X5 + X4*X6 + X7*X8
Матрица conf показывает, что линейные эффекты восьми факторов не смешаны с парными взаимодействиями. Парные взаимодействия смешаны друг с другом. Применение других генераторов не всегда позволяет достичь такого смешивания, например
>> [x, conf] = fracfact('a b c d ab cd ad bc')
x =
-1 -1 -1 -1 1 1 1 1
-1 -1 -1 1 1 -1 -1 1
-1 -1 1 -1 1 -1 1 -1
-1 -1 1 1 1 1 -1 -1
-1 1 -1 -1 -1 1 1 -1
-1 1 -1 1 -1 -1 -1 -1
-1 1 1 -1 -1 -1 1 1
-1 1 1 1 -1 1 -1 1
1 -1 -1 -1 -1 1 -1 1
1 -1 -1 1 -1 -1 1 1
1 -1 1 -1 -1 -1 -1 -1
1 -1 1 1 -1 1 1 -1
1 1 -1 -1 1 1 -1 -1
1 1 -1 1 1 -1 1 -1
1 1 1 -1 1 -1 -1 1
1 1 1 1 1 1 1 1
conf =
'Term' 'Generator' 'Confounding'
'X1' 'a' 'X1 + X2*X5 + X4*X7'
'X2' 'b' 'X2 + X1*X5 + X3*X8'
'X3' 'c' 'X3 + X2*X8 + X4*X6'
'X4' 'd' 'X4 + X1*X7 + X3*X6'
'X5' 'ab' 'X5 + X1*X2'
'X6' 'cd' 'X6 + X3*X4'
'X7' 'ad' 'X7 + X1*X4'
'X8' 'bc' 'X8 + X2*X3'
'X1*X2' 'ab' 'X5 + X1*X2'
'X1*X3' 'ac' 'X1*X3 + X5*X8 + X6*X7'
'X1*X4' 'ad' 'X7 + X1*X4'
'X1*X5' 'b' 'X2 + X1*X5 + X3*X8'
'X1*X6' 'acd' 'X1*X6 + X3*X7'
'X1*X7' 'd' 'X4 + X1*X7 + X3*X6'
'X1*X8' 'abc' 'X1*X8 + X3*X5'
'X2*X3' 'bc' 'X8 + X2*X3'
'X2*X4' 'bd' 'X2*X4 + X5*X7 + X6*X8'
'X2*X5' 'a' 'X1 + X2*X5 + X4*X7'
'X2*X6' 'bcd' 'X2*X6 + X4*X8'
'X2*X7' 'abd' 'X2*X7 + X4*X5'
'X2*X8' 'c' 'X3 + X2*X8 + X4*X6'
'X3*X4' 'cd' 'X6 + X3*X4'
'X3*X5' 'abc' 'X1*X8 + X3*X5'
'X3*X6' 'd' 'X4 + X1*X7 + X3*X6'
'X3*X7' 'acd' 'X1*X6 + X3*X7'
'X3*X8' 'b' 'X2 + X1*X5 + X3*X8'
'X4*X5' 'abd' 'X2*X7 + X4*X5'
'X4*X6' 'c' 'X3 + X2*X8 + X4*X6'
'X4*X7' 'a' 'X1 + X2*X5 + X4*X7'
'X4*X8' 'bcd' 'X2*X6 + X4*X8'
'X5*X6' 'abcd' 'X5*X6 + X7*X8'
'X5*X7' 'bd' 'X2*X4 + X5*X7 + X6*X8'
'X5*X8' 'ac' 'X1*X3 + X5*X8 + X6*X7'
'X6*X7' 'ac' 'X1*X3 + X5*X8 + X6*X7'
'X6*X8' 'bd' 'X2*X4 + X5*X7 + X6*X8'
'X7*X8' 'abcd' 'X5*X6 + X7*X8'
Как следует из анализа матрицы conf использование генератора 'a b c d ab cd ad bc' приводит к получению главных эффектов смешанных с парными взаимодействиями.
Графическое сравнение планов дробного и полного факторных экспериментов для трех факторов изменяющихся на двух уровнях.
>> n=3;
>> X = fracfact('a b ab')
X =
-1 -1 1
-1 1 -1
1 -1 -1
1 1 1
>> X = (X +1)/2
X =
0 0 1
0 1 0
1 0 0
1 1 1
>> x=X(:,1);
>> y=X(:,2);
>> z=X(:,3);
>> subplot(1,2,1)
>> plot3(x,y,z,'o')
>> grid on
>> Y = ff2n(n)
Y =
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
>> x1= Y (:,1);
>> y1= Y (:,2);
>> z1= Y (:,3);
>> subplot(1,2,2)
>> plot3(x1,y1,z1,'dr')
>> grid on
fullfact - Функция формирования плана полного факторного эксперимента для числа уровней факторов задаваемых пользователем
Синтаксис
design = fullfact(levels)
Описание
design = fullfact(levels) функция предназначена для генерации матрицы полного факторного эксперимента design при произвольном числе факторов и заданном количестве уровней для каждого фактора. Количество факторов и число уровней определяется вектором levels в формате levels=[n m k …], где n, m, k - число уровней первого, второго, третьего факторов и т.д. Элементы матрицы плана эксперимента представляются кодированными значениями и соответственно равны 1..n, 1..m, 1..k и т.д. 1 соответствует минимальному значению фактора и далее по возрастанию. Матрица плана эксперимента не рандомизирована и представляет собой последовательный перебор всех возможных комбинаций значений факторов.
Примеры использования функции генерации полного факторного эксперимента для произвольного числа и количества уровней факторов
Генерация матрицы плана эксперимента для трех факторов изменяющихся на 3 уровнях.
>> levels=[3 3 3]
levels =
3 3 3
>> design = fullfact(levels)
design =
1 1 1
2 1 1
3 1 1
1 2 1
2 2 1
3 2 1
1 3 1
2 3 1
3 3 1
1 1 2
2 1 2
3 1 2
1 2 2
2 2 2
3 2 2
1 3 2
2 3 2
3 3 2
1 1 3
2 1 3
3 1 3
1 2 3
2 2 3
3 2 3
1 3 3
2 3 3
3 3 3
Графически матрицу планирования эксперимента для трех факторов
изменяющихся на трех уровнях можно представить следующим образом
>> levels=[3 3 3];
>> design = fullfact(levels);
>> x=design(:,1);
>> y=design(:,2);
>> z=design(:,3);
>> plot3(x,y,z,'o')
>> grid on
Генерация матрицы плана эксперимента для трех факторов изменяющихся на 2x4x3 уровнях соответственно
>> levels=[2 4 3]
levels =
2 4 3
>> design = fullfact(levels)
design =
1 1 1
2 1 1
1 2 1
2 2 1
1 3 1
2 3 1
1 4 1
2 4 1
1 1 2
2 1 2
1 2 2
2 2 2
1 3 2
2 3 2
1 4 2
2 4 2
1 1 3
2 1 3
1 2 3
2 2 3
1 3 3
2 3 3
1 4 3
2 4 3
Графически матрицу планирования эксперимента для трех факторов изменяющихся на 2x4x3 уровнях
можно представить следующим образом
>> levels=[2 4 3]
>> design = fullfact(levels)
>> x=design(:,1);
>> y=design(:,2);
>> z=design(:,3);
>> plot3(x,y,z,'o')
>> grid on
hadamard - Матрица Адамара. Матрица Адамара соответствует плану дробного факторного эксперимента для факторов, каждый из которых задан на отрезке [-1 1]. И служит для построения линейной регрессионной модели. (Встроенная функция MATLAB)
Синтаксис
H = hadamard(n)
Описание
H = hadamard(n) функция предназначена для генерации матрицы Адамара n-го порядка. Матрица Адамара Н - это матрица с ортогональными столбцами, элементами которой являются 1 и -1, для которой должно выполняться условие
H'*H=n*I
где [n n] = size(H), I = eye(n,n).
Матрица Адамара размерностью nxn , при n>2, существует, если rem(n,4)=0. Для входного аргумента n должно выполняться условие - n, n/12, n/20 являются степенью 2.
Примеры использования функции генерации матрицы Адамара
Генерация матрицы Адамара с размерностью 4x4
>> H = hadamard(4)
H =
1 1 1 1
1 -1 1 -1
1 1 -1 -1
1 -1 -1 1
Проверка выполнения условия H'*H=n*I ,
>> n=4
n =
4
>> H = hadamard(4);
>> I = eye(n,n)
I =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> I*4==H'*H
ans =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
lhsdesign - План на основе латинских квадратов
Синтаксис
X = lhsdesign(n,p)
X = lhsdesign(...,'smooth','off')
X = lhsdesign(...,'criterion','c')
X = lhsdesign(...,'iterations',k)
Описание
X = lhsdesign(n,p) служит для генерации выборки латинского гиперкуба X, содержащую n значений для каждого значения переменной p (генерируется матрица размерностью n-p). Колонка матрицы содержит n случайных чисел полученных на одном из интервалов (0,1/n), (1/n,2/n), ..., (1-1/n,1) с последующей их случайной перестановкой.
Значение параметра 'smooth' определяет:
-
X = lhsdesign(...,'smooth','off') - случайную генерацию чисел из интервалов (0,1/n), (1/n,2/n), ..., (1-1/n,1);
-
X = lhsdesign(...,'smooth','on') - генерацию значений выборки как центральных точек указанных интервалов: 0.5/n, 1.5/n, ..., 1-0.5/n.
Значение параметра 'smooth' по умолчанию - 'on'.
Параметр 'criterion' задает итерационную процедуру генерации выборки латинского гиперкуба X в соответствии со значением 'c'. Возможные значения 'criterion' приведены в следующей таблице
|
'none' |
Отключение итерационной процедуры |
|
'maximin' |
Максимизация минимального расстояния между значениями выборки |
|
'correlation' |
Минимизация значения коэффициента корреляции |
Параметр 'iterations' позволяет задать число итераций k при генерации выборки X по итерационной процедуре. По умолчанию число итераций K=5.
План по латинскому гиперкубу используется в случаях, когда необходимо получить случайную многомерную выборку равномерно распределенную по каждому измерению.
Примеры использования функции генерации псевдослучайных чисел
Генерация матрицы латинского гиперкуба с размерностью 3-5.
>> n=3
n =
3
>> p=5
p =
5
>> X = lhsdesign(n,p)
X =
0.7987 0.3282 0.3561 0.3846 0.1093
0.5759 0.7511 0.8447 0.8249 0.7206
0.2671 0.5183 0.1938 0.2658 0.6601
Использование параметра 'smooth' для генерации матрицы латинского гиперкуба с размерностью 3-5.
>> X = lhsdesign(n,p,'smooth','off')
X =
0.5000 0.5000 0.8333 0.8333 0.1667
0.1667 0.8333 0.1667 0.1667 0.8333
0.8333 0.1667 0.5000 0.5000 0.5000
>> X = lhsdesign(n,p,'smooth','on')
X =
0.7205 0.0991 0.1018 0.6811 0.6090
0.4773 0.8178 0.7929 0.1591 0.6734
0.2099 0.5184 0.4017 0.3733 0.2429
Использование критерия генерации выборки латинского гиперкуба
>> X = lhsdesign(n,p,'criterion','none')
X =
0.1615 0.5914 0.1567 0.5401 0.8463
0.8887 0.1401 0.4532 0.7389 0.4774
0.5224 0.7465 0.9303 0.1064 0.0686
>> X = lhsdesign(n,p,'criterion', 'maximin')
X =
0.5600 0.5293 0.1867 0.9291 0.6221
0.6800 0.0851 0.3555 0.3869 0.2643
0.0911 0.9107 0.7722 0.1237 0.7976
>> X = lhsdesign(n,p,'criterion', 'correlation')
X =
0.9945 0.9808 0.4275 0.8485 0.9488
0.2700 0.5441 0.1024 0.5194 0.4415
0.4710 0.1228 0.9720 0.2156 0.1003
Генерация латинского гиперкуба с заданным числом итераций
X = lhsdesign(n,p,'criterion', 'correlation','iterations',10)
X =
0.1667 0.1667 0.8333 0.1667 0.5000
0.8333 0.8333 0.1667 0.8333 0.8333
0.5000 0.5000 0.5000 0.5000 0.1667
lhsnorm - Латинские квадраты для многомерной нормальной выборки
Синтаксис
X = lhsnorm(mu,SIGMA,n)
X = lhsnorm(mu,SIGMA,n,'onoff')
Описание
X = lhsnorm(mu,SIGMA,n) генерирует выборку латинского гиперкуба X размерностью n соответствующую многомерному нормальному распределению с вектором среднего mu и ковариационной матрицей SIGMA. Матрица SIGMA должна быть положительно определенной, квадратной и числом строк (столбцов) равным числу элементов в векторе mu. Выборка X распределена по многомерному нормальному закону. Предельным распределением каждой колонки массива является одномерный нормальный закон.
Параметр 'onoff' определяет коэффициент сглаживания выборки. Если 'onoff'='off', каждая колонка массива является перестановкой значений G(0.5/n), G(1.5/n), ..., G(1-0.5/n), где G обратная функция нормального распределения. Если 'onoff'='on' каждая колонка массива включает значения распределенные по равномерному закону. В этом случае, в качестве первого значения равного 0.5/n генерируется значение распределенное по закону равной вероятности на интервале (0/n,1/n). По умолчанию принимается 'onoff'='on'.
Примеры использования функции генерации псевдослучайных чисел
Генерация одного псевдослучайного числа
>> mu=1
mu =
1
>> SIGMA=1
SIGMA =
1
>> n=1
n =
1
>> X = lhsnorm(mu,SIGMA,n)
X =
2.5469
Генерация вектора случайных чисел
>> mu=1
mu =
1
>> SIGMA=1
SIGMA =
1
>> n=5
n =
5
>> X = lhsnorm(mu,SIGMA,n)
X =
-0.0472
1.1579
1.2965
0.6823
3.7835
Генерация матрицы псевдослучайных чисел с размерностью 2-5.
>> mu=[1 2]
mu =
1 2
>> n=5
n =
5
>> SIGMA=pascal(2)
SIGMA =
1 1
1 2
>> X = lhsnorm(mu,SIGMA,n)
X =
1.6009 3.2662
-0.5525 1.2473
1.9235 7.8638
0.4209 -0.3438
1.1730 1.8496
Генерация матрицы псевдослучайных чисел с размерностью 2-5 и использованием параметра 'onoff'.
>> mu=[1 2]
mu =
1 2
>> n=5
n =
5
>> SIGMA=pascal(2)
SIGMA =
1 1
1 2
>> X = lhsnorm(mu,SIGMA,n,'off')
X =
-0.2816 2.0000
1.0000 -0.5631
2.2816 3.0488
0.4756 0.9512
1.5244 4.5631
>> X = lhsnorm(mu,SIGMA,n,'on')
X =
0.7024 5.3389
1.3752 1.2876
0.7623 2.2380
2.0671 2.8099
-0.7103 -3.2271
rowexch - Функция для определения точного D-оптимального плана на основе алгоритма обмена строк
Синтаксис
settings = rowexch(nfactors,nruns)
[settings,X] = rowexch(nfactors,nruns)
[settings,X] = rowexch(nfactors,nruns,'model')
[settings,X] = rowexch(...,'param1',value1,'param2',value2,...)
Описание
settings = rowexch(nfactors,nruns) функция позволяет получить матрицу значений факторов D-оптимального плана settings на основе алгоритма перестановки строк в кодированных переменных, изменяющихся на двух уровнях (-1 - минимальное значение фактора, 1 - максимальное значение фактора). settings представляет собой матрицу D-оптимального плана эксперимента за исключением столбца соответствующего постоянному члену. Входными параметрами являются число факторов nfactors и количество опытов nruns. В качестве уравнения регрессии принимается линейная модель. Размерность матрицы settings равна nruns строк на nfactors столбцов.
[settings,X] = rowexch(nfactors,nruns) кроме матрицы значений факторов settings функция rowexch возвращает матрицу D-оптимального плана эксперимента Х.
[settings,X] = rowexch(nfactors,nruns,'model') этот вариант синтаксиса функции предусматривает генерацию матриц settings и Х для заданных числа факторов nfactors, количества опытов nruns и вида математической модели 'model'. Предусмотрены следующие виды математических моделей:
|
Значение 'model' |
Вид математической модели |
|
'linear' |
Линейная модель с постоянным членом. Значение по умолчанию. |
|
'interaction' |
Линейная модель с постоянным членом и эффектами взаимодействия. |
|
'quadratic' |
Полная квадратическая модель, включающая линейные, квадратические эффекты, эффекты взаимодействий, постоянный член. |
|
'purequadratic' |
Неполная квадратическая модель, включающая линейные, квадратические эффекты, постоянный член. |
[settings,X] = rowexch(...,'param1',value1,'param2',value2,...) кроме числа факторов nfactors, количества опытов nruns, вида математической модели 'model' предусмотрены следующие дополнительные входные аргументы:
|
'display' |
Вывод значения счетчика итераций. Возможные значения 'display': 'on' - вывод в командное окно, 'off' - отмена отображения. Значение по умолчанию 'on'. |
|
'init' |
Начальная матрица значений факторов с размерностью nruns x nfactors. По умолчанию предусматривается формирование начальной матрицы значений факторов случайным образом. |
|
'maxiter' |
Максимальное число итераций. Значение по умолчанию - 10. |
Дополнительные аргументы задаются в виде пары: 'название параметра', значение параметра.
Примечание. Функция rowexch осуществляет поиск D-оптимального плана на основе алгоритма перестановки строк. На первом этапе генерируется начальное множество точек в факторном пространстве, которые могут быть включены в план эксперимента. На втором этапе посредством перестановки строк в начальной матрице плана, формируется результирующая матрица плана эксперимента по критерию минимизации дисперсии коэффициентов уравнения регрессии. Если необходимо задать начальное множество точек отличное от генерируемого по умолчанию функцией rowexch используются функции candgen and candexch.
Примеры использования функции генерации матрицы D-оптимального плана на основе алгоритма перестановки строк
Генерация матрицы значений факторов D-оптимального плана для 4 факторов и 10 опытов
>>nfactors=4;
>> nruns=10;
>>settings = rowexch(nfactors,nruns)
settings =
-1 -1 1 1
-1 -1 -1 -1
1 1 1 -1
1 -1 1 1
-1 1 1 -1
1 -1 -1 -1
1 1 -1 1
-1 1 -1 1
-1 -1 1 1
1 -1 -1 -1
Генерация матрицы значений факторов и матрицы D-оптимального плана для 5 факторов и 12 опытов
>>nfactors=5;
>> nruns=12;
>>[settings,X] = rowexch(nfactors,nruns)
settings =
1 1 -1 -1 1
-1 -1 -1 -1 1
1 -1 -1 1 -1
1 -1 1 -1 -1
1 -1 1 -1 1
-1 -1 1 1 1
1 1 1 1 -1
-1 -1 -1 1 -1
-1 1 1 -1 -1
-1 1 1 1 1
-1 1 -1 -1 -1
1 1 -1 1 1
X =
1 1 1 -1 -1 1
1 -1 -1 -1 -1 1
1 1 -1 -1 1 -1
1 1 -1 1 -1 -1
1 1 -1 1 -1 1
1 -1 -1 1 1 1
1 1 1 1 1 -1
1 -1 -1 -1 1 -1
1 -1 1 1 -1 -1
1 -1 1 1 1 1
1 -1 1 -1 -1 -1
1 1 1 -1 1 1
Генерация матрицы значений факторов и матрицы D-оптимального плана для 4 факторов,
20 опытов и полной квадратической модели.
>>nfactors=4;
>> nruns=20;
>> model='quadratic';
>>[settings,X] = rowexch(nfactors,nruns,model)
settings =
1 -1 1 -1
0 0 0 0
-1 0 1 -1
-1 -1 1 0
1 1 -1 1
1 -1 1 1
1 0 -1 -1
0 -1 -1 1
1 1 1 -1
-1 -1 -1 -1
1 -1 -1 0
-1 1 -1 1
-1 -1 0 1
-1 1 0 -1
0 1 -1 -1
0 -1 0 -1
-1 1 1 1
1 1 1 1
-1 0 -1 0
1 1 0 0
X =
1 1 -1 1 -1 -1 1 -1 -1 1 -1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 -1 0 1 -1 0 -1 1 0 0 -1 1 0 1 1
1 -1 -1 1 0 1 -1 0 -1 0 0 1 1 1 0
1 1 1 -1 1 1 -1 1 -1 1 -1 1 1 1 1
1 1 -1 1 1 -1 1 1 -1 -1 1 1 1 1 1
1 1 0 -1 -1 0 -1 -1 0 0 1 1 0 1 1
1 0 -1 -1 1 0 0 0 1 -1 -1 0 1 1 1
1 1 1 1 -1 1 1 -1 1 -1 -1 1 1 1 1
1 -1 -1 -1 -1 1 1 1 1 1 1 1 1 1 1
1 1 -1 -1 0 -1 -1 0 1 0 0 1 1 1 0
1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 1 1 1
1 -1 -1 0 1 1 0 -1 0 -1 0 1 1 0 1
1 -1 1 0 -1 -1 0 1 0 -1 0 1 1 0 1
1 0 1 -1 -1 0 0 0 -1 -1 1 0 1 1 1
1 0 -1 0 -1 0 0 0 0 1 0 0 1 0 1
1 -1 1 1 1 -1 -1 -1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 -1 0 -1 0 0 1 0 0 0 0 1 0 1 0
1 1 1 0 0 1 0 0 0 0 0 1 1 0 0
Генерация матрицы значений факторов и матрицы D-оптимального плана для 4 факторов, 4 опытов и неполной квадратической модели. А является начальной матрицей для генерации D-оптимального плана эксперимента.
>>nfactors=4;
>> nruns=4;
>> model='purequadratic';
>> A=[1 0 1 0; 0 0 0 0; 1 1 1 1; 0 0 1 1]
A =
1 0 1 0
0 0 0 0
1 1 1 1
0 0 1 1
>>[settings,X] = rowexch(nfactors,nruns,model,'init',A)
settings =
-1 1 -1 1
1 -1 -1 -1
1 1 1 0
0 -1 1 1
X =
1 -1 1 -1 1 1 1 1 1
1 1 -1 -1 -1 1 1 1 1
1 1 1 1 0 1 1 1 0
1 0 -1 1 1 0 1 1 1
Графическое представление матрицы D-оптимального плана рассчитанной для 3 факторов,
12 опытов и полной квадратической модели
>>nfactors=3;
>> nruns=12;
>> model='quadratic';
>>settings = rowexch(nfactors,nruns,model)
settings =
-1 1 -1
0 0 -1
1 1 -1
1 -1 -1
1 1 1
-1 1 1
1 -1 1
-1 -1 -1
-1 -1 1
1 -1 0
-1 0 0
0 1 0
>> x= settings (:,1);
>> y= settings (:,2);
>> z= settings (:,3);
>> plot3(x,y,z,'o')
>> grid on
cluster - Деление иерархического дерева кластеров (группировка выходных данных функции linkage) на отдельные кластеры
Синтаксис
T = cluster(Z,'cutoff',c)
T = cluster(Z,'maxclust',n)
T = cluster(...,'criterion','crit')
T = cluster(...,'depth',d)
Описание
T = cluster(Z,'cutoff',c) функция предназначена для разделения на отдельные кластеры T иерархического дерева кластеров Z, полученного с помощью функции linkage. Входной параметр Z является матрицей с размерностью ![]() , где m - количество наблюдений многомерной случайной величины исходного множества данных. Входной параметр С - пороговая величина предназначенная для деления иерархического дерева Z на кластеры. Кластер формируется путем исключения связей иерархического дерева кластеров для которых значения коэффициентов несовместимости меньше величины С (подробнее см. описание функции inconsistent). Выходной параметр Т является вектором номеров кластеров к которым отнесены объекты исходного множества данных. Число элементов вектора Т равно m.
, где m - количество наблюдений многомерной случайной величины исходного множества данных. Входной параметр С - пороговая величина предназначенная для деления иерархического дерева Z на кластеры. Кластер формируется путем исключения связей иерархического дерева кластеров для которых значения коэффициентов несовместимости меньше величины С (подробнее см. описание функции inconsistent). Выходной параметр Т является вектором номеров кластеров к которым отнесены объекты исходного множества данных. Число элементов вектора Т равно m.
T = cluster(Z,'maxclust',n) входной параметр n определяет максимальное количество формируемых кластеров на которое делится иерархическое дерево кластеров Z.
T = cluster(...,'criterion','crit') входной параметр 'crit' определяет критерий формирования кластеров. Возможные значения: 'crit'='inconsistent', или 'crit'='distance'.
T = cluster(...,'depth',d) входной параметр d задает число вышележащих уровней иерархии в дереве кластеров при расчете коэффициентов несовместимости. Значение по умолчанию d=2. Коэффициент несовместимости служит для сравнения связи между двумя объектами в дереве кластеров с соседними восходящими связями на число вышележащих уровней иерархии.
Примеры использования функции кластеризации объектов по выходному параметру функции linkage
Кластеризация объектов по выходному параметру функции linkage. В качестве исходных данных используется 5-ти мерная случайная величина Х. Распределение Х является композицией нормального закона и закона Вейбулла. Сравнивается распределение объектов по кластерам для пороговой величины равной 0.1*(max(Z(:,3))), 0.3*(max(Z(:,3))), 0.4*(max(Z(:,3))). Графическое представление иерархического дерева кластеров выполняется с помощью функции dendrogram.
>> X=normrnd(0,1,15,5)+weibrnd(1,2,15,5);
>> Y = pdist(X);
>> Z = linkage(Y);
>> t1=0.1*(max(Z(:,3)));
>> t2=0.3*(max(Z(:,3)));
>> t3=0.4*(max(Z(:,3)));
>> dendrogram(Z);
.jpg)
>> T1 = cluster(Z,'cutoff', t1);
>> T2 = cluster(Z,'cutoff', t2);
>> T3 = cluster(Z,'cutoff', t3);
>> cat(2,T1,T2,T3)
ans =
3 3 1
3 3 1
1 1 2
2 2 5
4 4 3
1 1 2
8 8 3
9 9 4
7 7 1
5 5 2
6 6 5
10 10 6
4 4 3
2 2 5
11 11 7
Кластеризация объектов по выходному параметру функции linkage. В качестве исходных данных используется 10-ти мерная случайная величина Х. Объем выборки равен 25 элементам. Х распределена по нормальному закону. Графическое представление иерархического дерева кластеров выполняется с помощью функции dendrogram. Максимальное число кластеров принято равным 5.
>> X=normrnd(0,1,25,10);
>> Y = pdist(X);
>> Z = linkage(Y);
>> dendrogram(Z);
.jpg)
>> T = cluster(Z,'maxclust', 5)
T =
1
1
1
1
1
1
1
1
1
3
1
5
1
1
1
1
1
4
1
1
1
1
1
1
2
Кластеризация объектов по выходному параметру функции linkage. В качестве исходных данных используется 5-ти мерная случайная величина Х. Объем выборки равен 15 элементам. Х распределена по нормальному закону. Графическое представление иерархического дерева кластеров выполняется с помощью функции dendrogram. Критерий кластеризации 'crit'='distance'. Максимальное число кластеров принято равным 4.
>> X=normrnd(0,1,15,5);
>> Y = pdist(X);
>> Z = linkage(Y);
>> dendrogram(Z);
.jpg)
>> T = cluster(Z,'maxclust', 4, 'criterion', 'distance')
T =
3
1
1
1
1
1
1
1
4
2
1
1
1
1
1
Кластеризация объектов по выходному параметру функции linkage. В качестве исходных данных используется 10-ти мерная случайная величина Х. Объем выборки равен 20 элементам. Х распределена по нормальному закону. Графическое представление иерархического дерева кластеров выполняется с помощью функции dendrogram. Критерий кластеризации 'crit'='inconsistent'. Максимальное число кластеров принято равным 6. Число вышележащих уровней иерархии в дереве кластеров при расчете коэффициентов несовместимости принято равным 3.
>> X=normrnd(0,1,20,10);
>> Y = pdist(X);
>> Z = linkage(Y);
>> dendrogram(Z);
.jpg)
>> T = cluster(Z,'maxclust', 6, 'criterion', 'inconsistent', 'depth', 3)
T =
1
4
1
1
1
6
5
1
1
1
1
1
2
5
1
1
1
3
1
1
kmeans - Кластеризация на основе внутригрупповых средних
Синтаксис
IDX = kmeans(X,k)
[IDX,C] = kmeans(X,k)
[IDX,C,sumd] = kmeans(X,k)
[IDX,C,sumd,D] = kmeans(X,k)
[...] = kmeans(...,'param1',val1,'param2',val2,...)
Описание
IDX = kmeans(X, k) функция позволяет разделить множество исходных объектов, заданных матрицей Х, на k кластеров. Размерность Х равна ![]() , где n - количество наблюдений p-мерной случайной величины. Строки Х соответствуют наблюдениям, столбцы Х - признакам многомерной случайной величины. Процедура кластеризации является итерационной. Критерием кластеризации является минимум внутрикластерной суммы расстояний точек кластера до его центроида. Сумма расстояний находится по всем кластерам. В качестве расстояний точек кластера до его центроида используется квадрат евклидового расстояния. Функция возвращает вектор IDX индексов кластеров для каждого наблюдения многомерной случайной величины. Число элементов IDX равно n.
, где n - количество наблюдений p-мерной случайной величины. Строки Х соответствуют наблюдениям, столбцы Х - признакам многомерной случайной величины. Процедура кластеризации является итерационной. Критерием кластеризации является минимум внутрикластерной суммы расстояний точек кластера до его центроида. Сумма расстояний находится по всем кластерам. В качестве расстояний точек кластера до его центроида используется квадрат евклидового расстояния. Функция возвращает вектор IDX индексов кластеров для каждого наблюдения многомерной случайной величины. Число элементов IDX равно n.
[IDX,C] = kmeans(X,k) функция возвращает матрицу координат центроидов кластеров C. Размерность матрицы С равна ![]() .
.
[IDX,C,sumd] = kmeans(X,k) функция возвращает вектор сумм расстояний объектов кластера до его центроида sumd. Число элементов sumd равно k.
[IDX,C,sumd,D] = kmeans(X,k) функция возвращает матрицу расстояний объектов кластера до его центроида D. Размерность матрицы D равна ![]() .
.
[...] = kmeans(...,'param1',val1,'param2',val2,...) дополнительные входные параметры 'param1', 'param2', :, предназначены для управления работой алгоритма кластеризации и задаются в виде пары <название параметра, значение>. Предусмотрены следующие входные параметры и их значения:
|
Значение параметра 'param' |
Назначение параметра и его возможные значения, val |
|
|
'distance' |
Мера, используемая для расчета расстояний от объектов кластера до его центроида. Возможны следующие меры: |
|
|
|
'sqEuclidean' |
Квадрат Евклидового расстояния. Значение по умолчанию. Центроидом является среднее между объектами, образующими кластер. |
|
|
'cityblock' |
Расстояние по Манхеттену. Сумма абсолютных отклонений. Центроидом является медиана наблюдений, образующих кластер. |
|
|
'cosine' |
Косинусное расстояние. Определяется как единица минус косинус от угла между объектами, образующими кластер. Объекты в многомерном пространстве рассматриваются как векторы. Центроидом является среднее между объектами, образующими кластер, после приведения этих наблюдений к единицам евклидового расстояния. |
|
|
'correlation' |
Корреляционное расстояние. Определяется как единица минус выборочный коэффициент корреляции между значениями признаков многомерной случайной величины. Векторы наблюдений трактуются как выборки. Центроидом является среднее между объектами, образующими кластер, после центрирования этих наблюдений к нулевому среднему и последующей нормализации до единичной дисперсии. |
|
|
'Hamming' |
Расстояние Хэмминга. Определяется как процент отличающихся координат. Центроидом является медиана наблюдений, образующих кластер. |
|
'start' |
Способ определения начальных координат центроидов кластеров. |
|
|
|
'sample' |
Начальные координаты центроидов кластеров определяются как случайная выборка k наблюдений из матрицы Х. Значение по умолчанию. |
|
|
'uniform' |
Начальные координаты центроидов k кластеров выбираются случайным образом по равномерному закону из диапазона изменения многомерной случайной величины Х. 'uniform' не используется для 'distance'='Hamming'. |
|
|
'cluster' |
Выбор центроидов k кластеров выполняется на первичной фазе кластеризации. На первичной фазе производится выборка из Х, с объемом равным 10% от size(Х,1), и последующее определение начальных координат центроидов при 'start'='sample'. |
|
|
Значение задается пользователем в виде матрицы |
Размерность задаваемой пользователем матрицы начальных координат центроидов k кластеров равна |
|
'replicates' |
Число повторений процедуры кластеризации. Отдельная итерация выполняется при разных начальных координатах центроидов кластеров. Функция kmeans возвращает вектор решений IDX соответствующий минимальному значению sumd. Значение параметра 'replicates' может быть задано неявно, если параметр 'start' задан как трехмерный массив. В этом случае значением параметра 'replicates' является 3-я размерность 'start'. |
|
|
'maxiter' |
Максимальное количество итераций. Значение по умолчанию равно 100. |
|
|
'emptyaction' |
Действия kmeans в случае, если кластер теряет все свои наблюдения в процессе кластеризации. Возможные значения 'emptyaction': |
|
|
|
'error' |
Возникновение пустого кластера трактуется как ошибка. Значение по умолчанию. |
|
|
'drop' |
Все кластеры, ставшие пустыми, удаляются. Элементы выходных массивов C и D, соответствующие пустым кластерам, принимаются равными NaN. |
|
|
'singleton' |
Создается новый кластер, включающий одно наблюдение, дальнее от центроида пустого кластера. |
|
'display' |
Управление выходной информацией об итерациях kmeans. Возможные значения 'display': |
|
|
|
'off' |
Выходная информация не отображается. |
|
|
'iter' |
Отображается информация по каждой итерации в процессе минимизации внутрикластерной суммы расстояний объектов кластера до его центроида, включая номер итерации, фазу оптимизации, число задействованных объектов, общую сумму расстояний. |
|
|
'final' |
Отображается суммарная информация каждой итерации. |
|
|
'notify' |
Отображаются только предупреждения и сообщения об ошибках. Значение по умолчанию. |
Алгоритм kmeans
Функция kmeans использует итерационный алгоритм минимизации внутрикластерной суммы расстояний объектов кластера до его центроида по всем k кластерам, состоящий из двух этапов:
Первая фаза предназначена для поиска приближенного значения центроидов кластеров и предварительной группировки объектов в кластеры. Все объекты группируются в ближайшие к ним кластеры с последующим расчетом расстояний между объектами и центроидами. Однократное приближение при группировке всех объектов выполняется за одну итерацию.
Вторая фаза предназначена для поиска точного и окончательного решения. Группировка каждого из объектов по кластерам, с последующим расчетом его расстояния до центроида, на этой фазе выполняется по критерию минимизации внутрикластерной суммы расстояний объектов до центроидов кластеров. На каждой итерации расчет выполняется по всем объектам исходного множества.
Недостатком итерационного алгоритма функции kmeans является возможность попадания решения в локальный минимум внутрикластерной суммы расстояний точек кластера до его центроида по k кластерам. Эта проблема может быть решена соответствующим выбором начальной точки в начале процедуры кластеризации объектов.
Примеры использования функции кластеризации объектов по внутригрупповым средним
Кластеризация объектов на 5 групп по внутригрупповым средним. В качестве исходных данных используется нормально распределенная 10-ти мерная случайная величина. Количество объектов для кластеризации равно 20.
>> X=normrnd(0,1,20,10);
>> IDX = kmeans(X, 5)
IDX =
4
4
4
4
4
3
2
5
3
2
2
5
3
5
1
5
3
1
3
1
Кластеризация объектов на 4 кластера по внутригрупповым средним. В качестве исходных данных используется 8-ми мерная случайная величина. Количество объектов для кластеризации равно 20. Функция возвращает вектор индексов кластеров для наблюдений многомерной случайной величины, матрицу координат центроидов кластеров, вектор сумм расстояний объектов кластера до его центроида, матрицу расстояний объектов кластера до его центроида.
>> X=normrnd(0,1,20,8)+unifrnd(-3,3,20,8);
>> [IDX,C,sumd,D] = kmeans(X,4)
IDX =
4
3
1
1
1
2
1
1
2
2
3
1
1
4
4
3
4
2
2
4
C =
-0.7204 -0.7734 -2.0796 -0.0949 -0.9763 0.1793 0.4401 -0.9058
0.9580 -0.2410 0.9805 0.3499 0.3013 -0.9898 -1.6232 -2.4848
-0.6815 2.4138 -1.7521 0.9050 1.2935 2.5323 2.0555 0.7551
-1.8606 0.6397 -0.2230 -1.0799 -1.3034 1.3364 0.1347 2.6542
sumd =
108.2371
94.4057
55.7825
64.1026
D =
33.6258 69.6400 26.2378 14.6477
43.1736 60.0122 16.0955 44.7911
12.0549 28.5350 22.6655 27.7807
12.1929 40.6600 29.1959 38.2846
18.2936 53.6812 34.8565 58.8682
55.5411 33.5688 83.6597 85.3129
11.5506 40.2406 54.7996 32.3322
22.7636 49.0687 57.3729 38.5344
46.6591 16.8482 67.6677 57.4114
28.6118 6.2153 73.6534 62.9167
47.1499 82.2434 19.4972 50.7158
11.5096 25.0528 32.6233 25.2224
19.8718 27.8894 67.9857 40.6984
34.4482 65.2616 22.9467 12.0073
46.7967 50.9581 70.7584 22.6039
47.4286 78.3195 20.1898 39.1313
30.8704 49.9725 37.8780 5.7255
38.7515 20.2734 81.6425 84.9884
36.9069 17.5000 62.4367 52.2693
27.9929 76.7632 37.7078 9.1182
Кластеризация объектов на 5 кластеров по внутригрупповым средним. В качестве исходных данных используется 10-ти мерная равномерно распределенная случайная величина. Количество объектов для кластеризации равно 20. Функция возвращает вектор индексов кластеров для наблюдений многомерной случайной величины, матрицу координат центроидов кластеров, вектор сумм расстояний объектов кластера до его центроида, матрицу расстояний объектов кластера до его центроида. В качестве меры, используемой для расчета расстояний от объектов кластера до его центроида, используется расстояние Хэмминга.
>> X=unidrnd(2,20,10)-1;
>> [IDX,C,sumd,D] = kmeans(X,5,'distance', 'Hamming')
IDX =
1
1
4
3
4
2
4
5
5
4
3
5
5
2
4
3
5
1
2
1
C =
0 1 1 1 0 0 1 1 0 0
1 0 0 0 1 0 1 1 0 1
1 0 1 0 1 1 0 1 0 1
1 1 1 1 0 0 0 0 0 0
1 0 0 1 0 1 0 0 1 1
sumd =
0.7000
0.5000
0.6000
1.1000
1.1000
D =
0.2000 0.6000 0.5000 0.3000 0.6000
0 0.6000 0.7000 0.3000 0.8000
0.4000 0.6000 0.5000 0.3000 0.4000
0.6000 0.4000 0.1000 0.5000 0.6000
0.3000 0.7000 0.6000 0 0.5000
0.6000 0 0.3000 0.7000 0.6000
0.2000 0.6000 0.5000 0.1000 0.6000
0.9000 0.5000 0.4000 0.6000 0.1000
0.7000 0.7000 0.6000 0.4000 0.1000
0.5000 0.7000 0.6000 0.4000 0.5000
0.6000 0.2000 0.1000 0.7000 0.6000
0.8000 0.4000 0.3000 0.7000 0.2000
0.4000 0.6000 0.7000 0.5000 0.4000
0.8000 0.2000 0.3000 0.5000 0.4000
0.6000 0.4000 0.5000 0.3000 0.4000
0.5000 0.5000 0.4000 0.6000 0.5000
0.7000 0.5000 0.4000 0.4000 0.3000
0.3000 0.5000 0.8000 0.6000 0.7000
0.7000 0.3000 0.4000 0.8000 0.3000
0.2000 0.4000 0.5000 0.5000 0.8000
Кластеризация объектов на 5 кластеров по внутригрупповым средним. В качестве исходных данных используется 10-ти мерная случайная величина. Количество объектов для кластеризации равно 20. Функция возвращает вектор индексов кластеров для наблюдений многомерной случайной величины, матрицу координат центроидов кластеров, вектор сумм расстояний объектов кластера до его центроида, матрицу расстояний объектов кластера до его центроида. В качестве меры, используемой для расчета расстояний от объектов кластера до его центроида, используется расстояние по Манхеттену. Для определения начальных координат центроидов кластеров используется случайный выбор по равномерному закону из диапазона изменения многомерной случайной величины Х.
>> X=normrnd(0,1,30,10)+unifrnd(-3,3,30,10);
>> [IDX,C,sumd,D] = kmeans(X,5, 'distance', 'cityblock', 'start', 'uniform')
IDX =
1
1
5
5
4
3
3
4
5
3
3
4
2
2
4
3
4
3
2
4
4
4
1
3
2
4
5
5
4
2
C =
-0.4396 -1.3944 1.7663 -0.9604 -0.1684 1.6489 2.3836 -1.1063 1.4001 2.1388
0.1115 2.4586 -2.0031 -0.5451 -0.7847 -2.5797 1.1323 1.2079 -2.0007 0.6794
1.9904 -0.7443 0.2429 1.5091 1.3509 1.2865 -1.0615 -1.1467 0.0652 0.4982
0.9038 -0.9845 0.9931 0.7915 -0.0735 -1.2706 0.6240 0.4979 -0.1036 -1.6500
0.4969 2.0303 0.7973 -2.2842 0.5634 2.1423 1.1466 -1.5315 -1.4992 -2.3101
sumd =
27.7568
48.3109
70.4621
124.7830
61.5624
D =
11.0555 20.6961 16.2261 13.9733 21.9194
9.0177 30.0667 20.5845 23.9668 20.4227
18.0465 20.4097 20.4041 19.3285 10.0552
25.8682 19.5278 19.2421 17.4450 11.9428
15.9342 18.8171 16.1867 11.5907 17.5571
18.5595 20.2366 9.2825 17.4129 15.8366
20.5895 24.6483 8.9649 14.8240 23.3168
20.8177 21.2528 19.9603 15.2936 17.1220
15.3177 17.3140 15.9823 19.0280 9.3061
15.2568 26.3830 9.4391 17.6789 21.9894
16.3275 22.8697 8.6446 17.7723 22.7946
13.8266 19.1191 14.0988 12.1102 19.2555
14.3863 9.8094 16.3940 17.0357 15.2774
26.3103 9.7831 25.6021 19.4559 25.8235
23.7952 20.4040 24.9972 13.6631 21.7526
21.5771 23.3924 8.6547 13.8164 20.1203
19.3631 19.2680 18.5063 12.2459 19.8920
26.1242 29.7496 12.8143 19.0109 20.3680
24.4919 5.3314 21.6478 14.9553 19.8912
20.1819 20.5267 22.5905 18.1261 32.2715
20.0857 15.9628 20.4301 9.6275 19.9184
16.9443 20.9425 15.3291 11.3376 18.3866
7.6836 19.3235 14.9391 16.7161 16.1826
17.0445 18.8153 12.6620 15.4785 16.4266
24.0468 11.3653 19.6139 16.0655 22.8393
18.6036 19.2401 11.9422 6.4801 17.5061
22.7852 28.5627 22.9120 21.5459 14.6224
18.7729 16.8199 23.0108 22.1440 15.6359
27.2469 23.2618 18.2644 14.3082 23.6812
27.9308 12.0216 29.6800 26.3828 23.2369
Кластеризация объектов на 3 кластера по внутригрупповым средним. В качестве исходных данных используется 5-ти мерная случайная величина. Количество объектов для кластеризации равно 20. Функция возвращает вектор индексов кластеров для наблюдений многомерной случайной величины, матрицу координат центроидов кластеров, вектор сумм расстояний объектов кластера до его центроида, матрицу расстояний объектов кластера до его центроида. Для определения начальных координат центроидов кластеров используется матрица значений.
>> X=normrnd(0,1,30,5)+unifrnd(-3,3,30,5);
>> A=unifrnd(-1,1,3,5)+weibrnd(2,1,3,5);
>> [IDX,C,sumd,D] = kmeans(X,3, 'start',A)
IDX =
3
1
2
1
1
2
2
3
1
2
1
3
3
3
2
1
1
3
3
3
1
1
3
3
2
2
3
1
2
2
C =
-1.5886 0.4635 0.6624 -1.3072 1.3597
1.3848 0.3887 1.8371 -0.9976 -1.8332
0.6149 0.5035 -1.9144 0.5982 0.0231
sumd =
132.0303
93.1879
151.0349
D =
16.5360 11.0179 4.5584
19.0879 36.5566 35.6974
18.4315 7.6242 22.2605
6.9671 45.7506 40.8255
20.0426 33.0733 34.9800
22.0891 3.4413 28.8439
27.0650 7.5754 32.8361
13.6651 30.3022 3.2255
7.5434 18.2325 26.6683
45.8977 22.2643 45.6795
9.7168 18.8089 23.4718
30.6205 49.6317 23.0561
35.0507 32.0151 20.0662
20.5872 51.2292 10.3765
33.2640 4.4263 35.7963
20.3822 43.5634 36.2854
18.1425 39.9924 23.9586
47.2654 33.8941 18.4352
52.2725 29.3853 19.9980
24.2472 14.6352 10.2294
10.6090 30.1153 26.3401
12.9911 46.4257 39.9316
18.9980 47.0033 10.0471
56.8644 41.0418 22.3108
52.0324 11.5969 34.1655
20.8181 12.5828 38.3073
20.9826 38.2722 8.7317
6.5477 24.6831 13.0125
30.2170 8.4016 20.2688
28.0274 15.2751 21.0788
Кластеризация объектов на 3 кластера по внутригрупповым средним. В качестве исходных данных используется 5-ти мерная случайная величина. Количество объектов для кластеризации равно 20. Функция возвращает вектор индексов кластеров для наблюдений многомерной случайной величины, матрицу координат центроидов кластеров, вектор сумм расстояний объектов кластера до его центроида, матрицу расстояний объектов кластера до его центроида. Для определения начальных координат центроидов кластеров используется 3-х мерный массив значений С. Количество кластеров в kmeans задается первой размерностью С. Число повторений процедуры кластеризации определяется 3-й размерностью С.
>> X=normrnd(0,1,30,5)+unifrnd(-3,3,30,5);
>> A=unifrnd(-1,1,3,5)+weibrnd(2,1,3,5);
>> C = cat(3,A,A/2,A/5,A/10,A/100);
>> [IDX,C,sumd,D] = kmeans(X,[],'start',A)
IDX =
3
3
1
3
3
3
1
3
3
1
3
2
2
1
3
2
3
3
3
1
1
3
3
2
1
2
1
2
2
1
C =
-0.2008 -1.7141 -0.9325 0.6522 2.2468
-0.2522 -1.5345 2.7908 -1.2141 -0.4018
0.7738 1.1694 -0.2538 -0.0723 -0.3337
sumd =
93.8388
65.9418
185.3552
D =
20.4603 31.5608 13.6064
18.8331 14.5497 10.7444
12.0724 42.2282 32.2376
19.2397 16.3742 4.5067
9.5977 18.7638 6.6051
18.9974 26.1081 10.7523
10.6764 26.3081 29.8156
39.5376 31.4971 25.2423
13.8924 27.1870 3.4380
7.8997 48.9159 17.8625
31.9263 42.9726 14.0866
32.0669 12.9099 30.5786
25.3190 7.0696 9.2894
6.3914 48.6526 39.8010
39.0504 42.9705 11.9755
45.3934 4.7173 28.0688
38.4822 40.3342 23.5919
33.1447 58.4491 21.5793
37.1229 23.4369 13.8049
11.4012 34.5158 38.7785
17.2839 33.5309 27.2164
52.7047 43.2714 16.0919
49.0900 33.0580 9.3299
44.3969 8.0747 43.0688
4.0361 14.0509 11.0473
22.1320 11.5013 28.7823
15.1225 25.0779 29.9810
16.1192 6.0236 16.6442
51.2856 15.6455 42.0989
8.9552 40.1216 19.2787
Кластеризация объектов на 3 кластера по внутригрупповым средним. В качестве исходных данных используется 5-ти мерная случайная величина. Количество объектов для кластеризации равно 20. Функция возвращает вектор индексов кластеров для наблюдений многомерной случайной величины. Для определения начальных координат центроидов кластеров используется 3-х мерный массив значений С. Количество кластеров в kmeans задается первой размерностью С. Число повторений процедуры кластеризации определяется 3-й размерностью С. Максимальное количество итераций ограничено 25. Действия kmeans в случае, если кластер теряет все свои наблюдения в процессе кластеризации, заданы как 'singleton'. Выходная информация об итерациях kmeans отображается по каждой итерации.
>> X=normrnd(0,1,30,5)+unifrnd(-3,3,30,5);
>> A=unifrnd(-1,1,3,5)+weibrnd(2,1,3,5);
>> C = cat(3,A,A/2,A/5,A/10,A/100);
>> IDX = kmeans(X,[],'start',A, 'maxiter', 25, 'emptyaction', 'singleton', 'display', 'iter')
iter phase num sum
1 1 30 396.562
2 1 1 386.462
3 1 1 375.853
4 1 1 372.448
5 2 4 365.286
6 2 2 356.767
7 2 2 354.59
7 iterations, total sum of distances = 354.59
IDX =
2
2
3
3
3
2
3
3
3
3
3
2
1
1
1
1
1
2
2
3
3
3
2
1
2
1
3
2
2
1
linkage - Формирование иерархического дерева бинарных кластеров
Синтаксис
Z = linkage(Y)
Z = linkage(Y,'method')
Описание
Z = linkage(Y) функция позволяет сформировать иерархическое дерево бинарных кластеров с использованием алгоритма <ближайшего соседа>. Входной аргумент Y является вектором расстояний между парами объектов исходного множества данных в многомерном пространстве. Число элементов вектора Y равно ![]() , где
, где ![]() - количество объектов в исходном множестве данных. Y может быть получен как выходной параметр функции pdist. В общем случае входной аргумент Y может быть задан как матрица расстояний между парами объектов исходного множества данных, согласно формату выходного параметра функции pdist.
- количество объектов в исходном множестве данных. Y может быть получен как выходной параметр функции pdist. В общем случае входной аргумент Y может быть задан как матрица расстояний между парами объектов исходного множества данных, согласно формату выходного параметра функции pdist.
Выходной параметр Z является матрицей, содержащей информацию о дереве кластеров. Размерность Z равна ![]() . Конечные узлы дерева кластеров являются объектами исходного множества данных - наблюдений многомерной случайной величины Y, пронумерованных от 1 до m. Конечные узлы являются единичными кластерами. Они объединяются в кластеры вышележащими узлами дерева. Каждому последующему вышележащему узлу дерева кластеров соответствует i-я строка матрицы Z. Ему ставится в соответствие индекс m+i.
. Конечные узлы дерева кластеров являются объектами исходного множества данных - наблюдений многомерной случайной величины Y, пронумерованных от 1 до m. Конечные узлы являются единичными кластерами. Они объединяются в кластеры вышележащими узлами дерева. Каждому последующему вышележащему узлу дерева кластеров соответствует i-я строка матрицы Z. Ему ставится в соответствие индекс m+i.
Столбцы 1 и 2 матрицы Z содержат индексы объектов, связанных в новый кластер. Количество сформированных бинарных кластеров будет равно (m-1).
3-й столбец матрицы Z содержит значение расстояний между парами объектов, объединенных в кластеры.
Предположим, что дерево кластеров содержит 30 начальное узлов. Если 10-й кластер был сформирован объединением 5-го и 7-го объектов и расстояние между ними равно 1,5, тогда 10-я строка матрицы Z будет содержать следующие значения Z(:,10)=[5 6 1.5]. Этот кластер будет иметь индекс равный 10+30=40. Если 40 индекс будет обнаружен в последующих строках Z, то это означает, что 40 бинарный кластер будет объединен в новый вышележащий кластер.
Z = linkage(Y,'method') входной аргумент 'method' позволяет задать алгоритм кластеризации. Значение входного аргумента 'method' задается как тестовая строка. Предусмотрены следующие алгоритмы кластеризации
|
Значение 'method' |
Название алгоритма |
|
'single' |
Алгоритм <ближайшего соседа>. Значение по умолчанию. |
|
'complete' |
Алгоритм "дальнего соседа". |
|
'average' |
Алгоритм <средней связи>. |
|
'centroid' |
Центроидный алгоритм, использующий расстояние по <центрам тяжести> выборок. |
|
'ward' |
Пошаговый алгоритм. |
Формирование дерева кластеров основано на объединении двух нижележащих узлов в один вышележащий, и т.д. Критерием объединения узлов в кластер является отношение расстояний между парами объектов или кластеров. В linkage предусмотрены следующие меры расстояний между объектами:
|
Вид алгоритма |
Выражение для расчета расстояния между объектами |
|
Алгоритм <ближайшего соседа> |
где |
|
Алгоритм <дальнего соседа> |
Алгоритм <дальнего соседа> основан на определении наибольшего расстояния между объектами в двух группах. |
|
Алгоритм <средней связи> |
Алгоритм <средней связи> основан на расчете расстояний между всеми возможными парами объектов в кластерах r и s. |
|
Центроидный алгоритм |
где В результате применения центроидного алгоритма может быть получено не монотонное дерево кластеров. Это может произойти в случае, когда расстояние от объединения двух кластеров, |
|
Пошаговый алгоритм |
где |
Примеры использования функции формирования иерархического дерева бинарных кластеров
1. Формирование иерархического дерева бинарных кластеров для 10-ти мерной нормально распределенной случайной величины. Количество объектов в множестве исходных данных равно 20. Графическое представление дерева бинарных кластеров выполняется с помощью функции dendrogram.
>> X=normrnd(0,1,20,10);
>> Y = pdist(X);
>> Z = linkage(Y)
Z =
5.0000 20.0000 1.9330
7.0000 19.0000 2.0429
12.0000 15.0000 2.0979
6.0000 10.0000 2.3100
24.0000 22.0000 2.3239
1.0000 9.0000 2.3283
26.0000 21.0000 2.4018
27.0000 11.0000 2.4800
23.0000 16.0000 2.6409
4.0000 29.0000 2.6727
30.0000 14.0000 2.7020
28.0000 25.0000 2.7839
32.0000 3.0000 2.8100
33.0000 18.0000 2.8246
34.0000 31.0000 2.8279
35.0000 8.0000 2.8495
36.0000 13.0000 2.9005
37.0000 17.0000 2.9329
38.0000 2.0000 3.4541
>> H = dendrogram(Z);
.jpg)
2. Формирование иерархического дерева бинарных кластеров для 2-х мерной случайной величины. Количество объектов в множестве исходных данных равно 7. Сравниваются различные алгоритмы кластеризации. Графическое представление результатов кластеризации выполняется с помощью функции dendrogram.
2.1. Исходные данные:
>> X = [3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1]
X =
3.0000 1.7000
1.0000 1.0000
2.0000 3.0000
2.0000 2.5000
1.2000 1.0000
1.1000 1.5000
3.0000 1.0000
>> Y = pdist(X);
Y =
Columns 1 through 11
2.1190 1.6401 1.2806 1.9313 1.9105 0.7000 2.2361 1.8028 0.2000 0.5099 2.0000
Columns 12 through 21
0.5000 2.1541 1.7493 2.2361 1.7000 1.3454 1.8028 0.5099 1.8000 1.9647
2.2. Кластеризация при помощи алгоритма <ближайшего соседа>
>> Z = linkage(Y, 'single')
Z =
2.0000 5.0000 0.2000
3.0000 4.0000 0.5000
8.0000 6.0000 0.5099
1.0000 7.0000 0.7000
11.0000 9.0000 1.2806
12.0000 10.0000 1.3454
>> dendrogram(Z);
.jpg)
2.3. Кластеризация при помощи алгоритма <дальнего соседа>
>> Z = linkage(Y, 'complete')
Z =
2.0000 5.0000 0.2000
3.0000 4.0000 0.5000
8.0000 6.0000 0.5099
1.0000 7.0000 0.7000
11.0000 10.0000 2.1190
12.0000 9.0000 2.2361
>> dendrogram(Z);
.jpg)
2.4. Кластеризация при помощи алгоритма <средней связи>
>> Z = linkage(Y, 'average')
Z =
2.0000 5.0000 0.2000
3.0000 4.0000 0.5000
8.0000 6.0000 0.5099
1.0000 7.0000 0.7000
11.0000 9.0000 1.7399
12.0000 10.0000 1.8928
>> dendrogram(Z);
.jpg)
2.5. Кластеризация при помощи алгоритма центроидного алгоритма
>> Z = linkage(Y, 'centroid')
Warning: Non-monotonic cluster tree -- the centroid method is probably not appropriate.
> In C:\MATLAB6p5p1\toolbox\stats\linkage.m at line 165
Z =
2.0000 5.0000 0.2000
8.0000 6.0000 0.5000
3.0000 4.0000 0.5000
1.0000 7.0000 0.7000
11.0000 10.0000 1.7205
12.0000 9.0000 1.6554
>> dendrogram(Z);
.jpg)
2.6. Кластеризация при помощи алгоритма пошагового алгоритма
>> Z = linkage(Y, 'ward')
Z =
2.0000 5.0000 0.1414
3.0000 4.0000 0.3536
8.0000 6.0000 0.4082
1.0000 7.0000 0.4950
11.0000 9.0000 1.7205
12.0000 10.0000 2.1674
>> dendrogram(Z);
.jpg)
pdist - Расчет парных расстояний между объектами (векторами) в исходном множестве данных
Синтаксис
Y = pdist(X)
Y = pdist(X,'metric')
Y = pdist(X,distfun,p1,p2,...)
Y = pdist(X,'minkowski',p)
Описание
Y = pdist(X) функция позволяет рассчитать вектор Евклидовых расстояний Y между парами объектов исходного множества данных, заданных матрицей Х. Размерность матрицы Х равна ![]() , где m - число наблюдений n-мерной случайной величины. Количество пар расстояний для m наблюдений многомерной случайной величины, или иначе mобъектов, будет определяться по формуле
, где m - число наблюдений n-мерной случайной величины. Количество пар расстояний для m наблюдений многомерной случайной величины, или иначе mобъектов, будет определяться по формуле ![]() .
.
Выходной параметр Y является вектором, содержащим значения парных расстояний между объектами. Число элементов Y равно ![]() . Расстояния между объектами в векторе Y расположены в следующем порядке (1,2), (1,3), ..., (1,m), (2,3),...,(i,j),..., (2,m), ..., ..., (m-1,m), где i, j - номера строк матрицы Х.
. Расстояния между объектами в векторе Y расположены в следующем порядке (1,2), (1,3), ..., (1,m), (2,3),...,(i,j),..., (2,m), ..., ..., (m-1,m), где i, j - номера строк матрицы Х.
При помощи функции squareform вектор Y можно конвертировать в квадратную матрицу. Элемент (i, j) полученной матрицы, при i<j, будет соответствовать расстоянию между i-м и j-м объектами исходного множества данных:
>> X=normrnd(0,1,7,3)
X =
0.6353 0.4620 -0.1132
-0.6014 -0.3210 0.3792
0.5512 1.2366 0.9442
-1.0998 -0.6313 -2.1204
0.0860 -2.3252 -0.6447
-2.0046 -1.2316 -0.7043
-0.4931 1.0556 -1.0181
>> Y = pdist(X)
Y =
Columns 1 through 11
1.5444 1.3134 2.8696 2.8902 3.1917 1.5635 2.0183 2.5677 2.3532 1.9930 1.9646
Columns 12 through 21
3.9505 3.9277 3.9168 2.2302 2.5404 1.7845 2.1045 2.3601 3.4504 2.7595
>> S = squareform(Y)
S =
0 1.5444 1.3134 2.8696 2.8902 3.1917 1.5635
1.5444 0 2.0183 2.5677 2.3532 1.9930 1.9646
1.3134 2.0183 0 3.9505 3.9277 3.9168 2.2302
2.8696 2.5677 3.9505 0 2.5404 1.7845 2.1045
2.8902 2.3532 3.9277 2.5404 0 2.3601 3.4504
3.1917 1.9930 3.9168 1.7845 2.3601 0 2.7595
1.5635 1.9646 2.2302 2.1045 3.4504 2.7595 0
Y = pdist(X,'metric') входной параметр 'metric' определяет вид расстояния между объектами исходного множества данных. 'metric' задается как строковая переменная. Предусмотрены следующие виды расстояний между объектами:
|
Значение параметра 'metric' |
Метод расчета расстояний между объектами |
|
'euclidean' |
Евклидово расстояние. Значение по умолчанию. |
|
'seuclidean' |
Нормализованное евклидово расстояние. |
|
'mahalanobis' |
Расстояние Махаланобиса. |
|
'cityblock' |
Расстояние по Манхеттену. Определяется как сумма абсолютных величин отклонений по всем измерениям. |
|
'minkowski' |
Метрика Минковского |
|
'cosine' |
Косинусное расстояние. Определяется как единица минус косинус от угла между объектами. Объекты в многомерном пространстве рассматриваются как векторы. |
|
'correlation' |
Корреляционное расстояние. Определяется как единица минус выборочный коэффициент корреляции между значениями признаков многомерной случайной величины. Векторы наблюдений трактуются как выборки. |
|
'hamming' |
Расстояние Хэмминга. Определяется как процент отличных координат от их общего числа. |
|
'jaccard' |
Расстояние Джаккарда. Определяется как единица минус коэффициент Джаккарда. Коэффициентом Джаккарда является процент отличающихся ненулевых координат от их общего числа. |
Y = pdist(X,distfun,p1,p2,...) входной параметр distfun является указателем на функцию расчета парных расстояний между объектами задаваемой пользователем в виде:
d = distfun(XI,XJ,p1,p2,...).
Функция distfun получает две матрицы XI, XJ, содержащих строки матрицы Х. Размерность матриц XI, XJ равна ![]() . Необязательные входные параметры p1,p2,... непрямую передаются функции distfun из pdist. Функция distfun должна возвратить вектор расстояний d. Элемент d(k) является расстоянием между наблюдениями XI(k,:) и XJ(k,:).
. Необязательные входные параметры p1,p2,... непрямую передаются функции distfun из pdist. Функция distfun должна возвратить вектор расстояний d. Элемент d(k) является расстоянием между наблюдениями XI(k,:) и XJ(k,:).
Y = pdist(X,'minkowski',p) функция служит для расчета парных расстояний между объектами, определяемыми матрицей Х, с использованием метрики Минковского. Входной параметр р является показателем степени метрики Минковского. По умолчанию р=2.
Виды парных расстояний между объектами, используемые в pdist:
1. Евклидово расстояние:
![]() ,
,
где ![]() ,
, ![]() - r и s строки матрицы Х,
- r и s строки матрицы Х, ![]() ,
, ![]() .
.
2. Стандартизованное Евклидово расстояние:
![]() ,
,
где ![]() - диагональная матрица. Диагональными элементами
- диагональная матрица. Диагональными элементами ![]() являются выборочные дисперсии признаков многомерной случайной величины Xj ,j=1..m.
являются выборочные дисперсии признаков многомерной случайной величины Xj ,j=1..m.
3. Расстояние Махаланобиса:
![]() ,
,
где ![]() - ковариационная матрица, рассчитанная по выборке Х.
- ковариационная матрица, рассчитанная по выборке Х.
4. Расстояние по Манхеттену:
![]() .
.
5. Метрика Минковского:
.gif) .
.
При ![]() метрика Минковского эквивалентна расстоянию по Манхеттену. При
метрика Минковского эквивалентна расстоянию по Манхеттену. При ![]() метрика Минковского превращается в Евклидово расстояние.
метрика Минковского превращается в Евклидово расстояние.
6. Косинусное расстояние:
.gif) .
.
7. Корреляционное расстояние:
.gif) ,
,
где ![]() ,
, ![]() .
.
Определяется как единица минус выборочный коэффициент корреляции между значениями признаков многомерной случайной величины. Векторы наблюдений трактуются как выборки.
8. Расстояние Хэмминга:
![]() .
.
9. Расстояние Джаккарда:
.gif) .
.
Примеры использования функции расчета парных расстояний между объектами исходного множества данных
1. Расчет парных расстояний между объектами исходного множества данных. В качестве исходного множества данных используется двумерная случайная величина. Количество объектов в множестве исходных данных равно 7.
>> X = [3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1]
X =
3.0000 1.7000
1.0000 1.0000
2.0000 3.0000
2.0000 2.5000
1.2000 1.0000
1.1000 1.5000
3.0000 1.0000
>> Y = pdist(X)'
Y =
2.1190
1.6401
1.2806
1.9313
1.9105
0.7000
2.2361
1.8028
0.2000
0.5099
2.0000
0.5000
2.1541
1.7493
2.2361
1.7000
1.3454
1.8028
0.5099
1.8000
1.9647
2. Расчет парных расстояний между объектами исходного множества данных. В качестве исходного множества данных используется двумерная случайная величина. Количество объектов в множестве исходных данных равно 7. Сравниваются евклидово расстояние, нормализованное евклидово расстояние, расстояние Махаланобиса, расстояние по Манхеттену, метрика Минковского, косинусное расстояние, расстояние Хэмминга, расстояние Джаккарда.
>> X = [3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1]
X =
3.0000 1.7000
1.0000 1.0000
2.0000 3.0000
2.0000 2.5000
1.2000 1.0000
1.1000 1.5000
3.0000 1.0000
>> Y1 = pdist(X, 'euclidean')';
>> Y2 = pdist(X, 'seuclidean')';
>> Y3 = pdist(X, 'mahalanobis')';
>> Y4 = pdist(X, 'cityblock')';
>> Y5 = pdist(X, 'minkowski')';
>> Y6 = pdist(X, 'cosine')';
>> Y7 = pdist(X, 'hamming')';
>> Y8 = pdist(X, 'jaccard')';
>> Y = [Y1'; Y2'; Y3'; Y4'; Y5'; Y6'; Y7'; Y8']'
Y =
2.1190 2.4992 2.3879 2.7000 2.1190 0.0362 1.0000 1.0000
1.6401 2.0036 2.1983 2.3000 1.6401 0.1072 1.0000 1.0000
1.2806 1.5399 1.6946 1.8000 1.2806 0.0715 1.0000 1.0000
1.9313 2.2815 2.1684 2.5000 1.9313 0.0160 1.0000 1.0000
1.9105 2.2378 2.2284 2.1000 1.9105 0.0879 1.0000 1.0000
0.7000 0.8757 0.8895 0.7000 0.7000 0.0187 0.5000 0.5000
2.2361 2.7621 2.6097 3.0000 2.2361 0.0194 1.0000 1.0000
1.8028 2.2115 2.0616 2.5000 1.8028 0.0061 1.0000 1.0000
0.2000 0.2341 0.2378 0.2000 0.2000 0.0041 0.5000 0.5000
0.5099 0.6363 0.6255 0.6000 0.5099 0.0116 1.0000 1.0000
2.0000 2.3408 2.3778 2.0000 2.0000 0.1056 0.5000 0.5000
0.5000 0.6255 0.6353 0.5000 0.5000 0.0038 0.5000 0.5000
2.1541 2.6713 2.5522 2.8000 2.1541 0.0412 1.0000 1.0000
1.7493 2.1518 2.0153 2.4000 1.7493 0.0010 1.0000 1.0000
2.2361 2.7621 2.9890 3.0000 2.2361 0.2106 1.0000 1.0000
1.7000 2.0970 1.9750 2.3000 1.7000 0.0202 1.0000 1.0000
1.3454 1.6354 1.5106 1.9000 1.3454 0.0009 1.0000 1.0000
1.8028 2.2115 2.4172 2.5000 1.8028 0.1604 1.0000 1.0000
0.5099 0.6363 0.6666 0.6000 0.5099 0.0295 1.0000 1.0000
1.8000 2.1067 2.1400 1.8000 1.8000 0.0688 0.5000 0.5000
1.9647 2.3101 2.4517 2.4000 1.9647 0.1840 1.0000 1.0000
3. Расчет парных расстояний между объектами исходного множества данных. В качестве исходного множества данных используется двумерная случайная величина. Количество объектов в множестве исходных данных равно 7. В качестве расстояния между объектами исходного множества данных используется функция пользователя.
3.1. Текст функции взвешенного евклидового расстояния weucldist.m
function d = weucldist(XI, XJ, W)
% Функция реализующая взвешенное евклидово расстояние
d = sqrt((XI-XJ).^2 * W');
3.2. Использование pdist и функции расчета расстояний, определенной пользователем. Wgts - вектор весов. Число признаков X должно быть равно количеству элементов в Wgts/
>> X = [3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1]
X =
3.0000 1.7000
1.0000 1.0000
2.0000 3.0000
2.0000 2.5000
1.2000 1.0000
1.1000 1.5000
3.0000 1.0000
>> Wgts = [.1 .3];
>> Ywgt = pdist(X, @weucldist, Wgts)
Ywgt =
Columns 1 through 11
0.7396 0.7791 0.5404 0.6863 0.6107 0.3834 1.1402 0.8803 0.0632 0.2757 0.6325
Columns 12 through 21
0.2739 1.1243 0.8695 1.1402 0.8597 0.6173 0.8803 0.2757 0.5692 0.6603
4. Расчет парных расстояний между объектами исходного множества данных. В качестве исходного множества данных используется двумерная случайная величина. Количество объектов в множестве исходных данных равно 7. В качестве расстояния между объектами используется метрика Минковского с показателем степени равным 1, 2, 3.
>> X = [3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1]
X =
3.0000 1.7000
1.0000 1.0000
2.0000 3.0000
2.0000 2.5000
1.2000 1.0000
1.1000 1.5000
3.0000 1.0000
>> Y1 = pdist(X,'minkowski',1)';
>> Y2 = pdist(X,'minkowski',2)';
>> Y3 = pdist(X,'minkowski',3)';
>> Y = [Y1'; Y2'; Y3']'
Y =
2.7000 2.1190 2.0282
2.3000 1.6401 1.4732
1.8000 1.2806 1.1478
2.5000 1.9313 1.8346
2.1000 1.9105 1.9007
0.7000 0.7000 0.7000
3.0000 2.2361 2.0801
2.5000 1.8028 1.6355
0.2000 0.2000 0.2000
0.6000 0.5099 0.5013
2.0000 2.0000 2.0000
0.5000 0.5000 0.5000
2.8000 2.1541 2.0418
2.4000 1.7493 1.6010
3.0000 2.2361 2.0801
2.3000 1.7000 1.5723
1.9000 1.3454 1.2002
2.5000 1.8028 1.6355
0.6000 0.5099 0.5013
1.8000 1.8000 1.8000
2.4000 1.9647 1.9115
factoran - Факторный анализ
Синтаксис
lambda = factoran(X,m)
[lambda,psi] = factoran(X,m)
[lambda,psi,T] = factoran(X,m)
[lambda,psi,T,stats] = factoran(X,m)
[lambda,psi,T,stats,F] = factoran(X,m)
[...] = factoran(...,'param1',value1,'param2',value2,...)
Описание
Модель простого факторного анализа может быть представлена в виде
|
|
(1) |
где ![]() - вектор наблюдений многомерной случайной величины,
- вектор наблюдений многомерной случайной величины, ![]() - матрица нагрузок простых факторов,
- матрица нагрузок простых факторов, ![]() - вектор средних значений признаков многомерной случайной величины
- вектор средних значений признаков многомерной случайной величины ![]() ,
, ![]() - вектор взаимно независимых, стандартизованных факторов,
- вектор взаимно независимых, стандартизованных факторов, ![]() - вектор независимых специфических факторов. Вектор значений многомерной случайной величины равен
- вектор независимых специфических факторов. Вектор значений многомерной случайной величины равен ![]() , где
, где ![]() - i-й признак многомерной случайной величины. Размерность матрицы
- i-й признак многомерной случайной величины. Размерность матрицы ![]() равна
равна ![]() , где
, где ![]() - число специфических факторов, или размерность многомерной случайной величины
- число специфических факторов, или размерность многомерной случайной величины ![]() ,
, ![]() - число простых факторов. Элемент матрицы
- число простых факторов. Элемент матрицы ![]() называется нагрузкой i-й переменной на j-й фактор, или наоборот, нагрузкой j-го фактора на i-ю переменную. Число элементов векторов
называется нагрузкой i-й переменной на j-й фактор, или наоборот, нагрузкой j-го фактора на i-ю переменную. Число элементов векторов ![]() ,
, ![]() и
и ![]() равно
равно ![]() .
.
Другой формой записи модели простого факторного анализа является выражение
|
|
(2) |
где ![]() .
. ![]() является диагональной матрицей дисперсий независимых специфических факторов. Размерность матрицы
является диагональной матрицей дисперсий независимых специфических факторов. Размерность матрицы ![]() равна
равна ![]() .
.
Как следует из (1) или (2), значение признака многомерной случайной величины ![]() может быть выражено суммой взвешенных простых факторов
может быть выражено суммой взвешенных простых факторов ![]() и остаточного члена
и остаточного члена ![]() . Весами простых факторов
. Весами простых факторов ![]() являются элементы матрицы нагрузок
являются элементы матрицы нагрузок ![]() . Количество простых факторов
. Количество простых факторов ![]() должно быть меньше числа признаков многомерной случайной величины
должно быть меньше числа признаков многомерной случайной величины ![]() . Это позволяет уменьшить размерность задачи с
. Это позволяет уменьшить размерность задачи с ![]() до
до ![]() . В простом факторном анализе предполагается, что простые факторы взаимно независимы и их дисперсии равны единице, а специфические факторы
. В простом факторном анализе предполагается, что простые факторы взаимно независимы и их дисперсии равны единице, а специфические факторы ![]() не зависимы от какого либо
не зависимы от какого либо ![]() , где
, где ![]() ,
, ![]() . Максимально возможное количество простых факторов
. Максимально возможное количество простых факторов ![]() определяется неравенством
определяется неравенством
![]() .
.
Сумму квадратов нагрузок соответствующих ![]() называют общностью i-го признака. Общность характеризует часть дисперсии
называют общностью i-го признака. Общность характеризует часть дисперсии ![]() , которая объясняется простыми факторами
, которая объясняется простыми факторами ![]() . Величина
. Величина ![]() показывает какая часть дисперсии
показывает какая часть дисперсии ![]() i-го признака остается необъясненной для выбранного набора простых факторов
i-го признака остается необъясненной для выбранного набора простых факторов ![]() . Эту величину называют специфичностью i-го признака.
. Эту величину называют специфичностью i-го признака.
Коэффициент корреляции двух признаков ![]() и
и ![]() можно выразить суммой произведений нагрузок некоррелированных факторов
можно выразить суммой произведений нагрузок некоррелированных факторов
![]() .
.
Задача факторного анализа, расчет матрицы нагрузок ![]() для заданного вектора
для заданного вектора ![]() , не имеет однозначного решения. Представление ковариационной матрицы признаков многомерной случайной величины Х, cov(Х), факторами
, не имеет однозначного решения. Представление ковариационной матрицы признаков многомерной случайной величины Х, cov(Х), факторами ![]() , или иначе факторизацию cov(Х), можно провести бесконечно большим числом способов. Если найдена матрица нагрузок, то любое линейное ортогональное преобразование
, или иначе факторизацию cov(Х), можно провести бесконечно большим числом способов. Если найдена матрица нагрузок, то любое линейное ортогональное преобразование ![]() , или иначе ортогональное вращение
, или иначе ортогональное вращение ![]() , приведет к такой же факторизации по модели (1).
, приведет к такой же факторизации по модели (1).
lambda = factoran(X,m) функция предназначена для расчета матрицы нагрузок lambda методом максимального правдоподобия для m простых факторов. Входной параметр Х является матрицей наблюдений многомерной случайной величины. Строки Х соответствуют наблюдениям, столбцы Х - признакам многомерной случайной величины. Размерность Х равна n×d, где n - число наблюдений, d - количество признаков многомерной случайной величины. Входной параметр m должен быть задан как скаляр. Размерность матрицы нагрузок lambda равна d×m. lambda(i,j) является нагрузкой j-го фактора на i-й признак многомерной случайной величины. По умолчанию, при оценке lambda используется метод ортогонального вращения варимакс, позволяющий упростить столбцы матрицы нагрузок, сводя значения к 1 или 0.
[lambda,psi] = factoran(X,m) функция возвращает выходной параметр psi - вектор точечных оценок дисперсий специфических факторов, рассчитанный методом максимального правдоподобия. Число элементов вектора psi равно d.
[lambda,psi,T] = factoran(X,m) функция возвращает матрицу вращения нагрузок Т. Размерность Т равна m×m.
[lambda,psi,T,stats] = factoran(X,m) функция возвращает структуру stats, позволяющую проверить нулевую гипотезу H0. H0 состоит в том, что число простых факторов равно m. stats содержит следующие поля:
|
stats.loglike |
Значение логарифма функции максимального правдоподобия |
|
stats.dfe |
Число степеней свободы погрешности, определяемое как ((d-m)^2 - (d+m))/2 |
|
stats.chisq |
Значение статистики хи-квадрат, предназначенное для проверки нулевой гипотезы |
|
stats.p |
Значение уровня значимости, соответствующее выборочной статистике stats.chisq. При расчете stats.p используется правосторонняя критическая область. |
Значение полей stats.chisq и stats.p будут рассчитаны в случае, если stats.dfe>0 и все элементы вектора psi будут положительными. Если входной параметр Х будет задан как ковариационная матрица, то для расчета stats.chisq и stats.p необходимо определить значение дополнительного входного параметра 'nobs'.
[lambda,psi,T,stats,F] = factoran(X,m) функция возвращает, рассчитанные по модели (1), значения многомерной случайной величины F. Расчет значений многомерной случайной величины проводится для m простых факторов, по рассчитанной матрице нагрузок lambda. F является матрицей с размерностью n×m. Строки матрицы F соответствуют наблюдениям, а столбцы - признакам многомерной случайной величины. F не может быть рассчитана, если входной параметр Х задан как ковариационная матрица.
[...] = factoran(...,'param1',value1,'param2',value2,...) управление работой алгоритма функции factoran осуществляется с помощью дополнительных входных параметров 'param1', 'param2', :. Дополнительные входные параметры задаются в виде пары <название параметра, значение> и их возможные значения приведены в следующей таблице:
|
Дополнительный входной параметр 'param' |
Назначение 'param' и его возможные значения, value |
|
|
'xtype' |
Вид исходных данных Х: |
|
|
'data' |
Х задается как матрица наблюдений значений многомерной случайной величины. Значение по умолчанию. |
|
|
'covariance' |
Х задана как положительно определенная ковариационная или корреляционная матрица. |
|
|
'scores' |
Метод расчета значений многомерной случайной величины F по модели (1). Параметр 'scores' игнорируется, если Х задана как ковариационная или корреляционная матрица. Возможные значения 'scores': |
|
|
'wls' 'Bartlett' |
Оценка значений элементов матрицы F выполняется по методу взвешенных наименьших квадратов. Значение по умолчанию. |
|
|
'regression' 'Thomson' |
Расчет F производится с использованием критерия минимума средней квадратической ошибки, что эквивалентно ридж-регрессии. |
|
|
'start' |
Начальное значение дисперсий специфических факторов psi для процедуры оптимизации методом максимального правдоподобия. Возможные значения 'start': |
|
|
'random' |
Вектор дисперсией генерируется по непрерывному закону равной вероятности в интервале возможных значений [0,1]. Число элементов вектора дисперсий равно d. |
|
|
'Rsquared' |
Начальные вектор дисперсий рассчитывается из выражения diag(inv(corrcoef(X))). Значение по умолчанию. |
|
|
Целое положительное значение |
Вектор дисперсией генерируется по непрерывному закону равной вероятности в интервале возможных значений [0,1], 'start'='random'. Расчет выходных параметров выполняется заданное целым числом количество раз. Функция factoran возвращает результат расчета соответствующий максимальному значению функции правдоподобия. |
|
|
Matrix |
Начальное значение дисперсий специфических факторов задается в виде матрицы. Столбцы матрицы соответствуют векторам начальных приближений для дисперсий специфических факторов. Количество строк матрицы начальных приближений должно быть равно d. |
|
|
'rotate' |
Метод вращения матрицы нагрузок и расчета значений многомерной случайной величины |
|
|
'none' |
Вращение отсутствует |
|
|
'orthomax' |
Ортогональное вращение. Критерием оптимизации матрицы нагрузок при ортогональном вращении является максимум дисперсии объясненной простыми факторами. Приведенные ниже дополнительные входные параметры 'coeffom', 'normalize', 'reltol', 'maxit' предназначены для управления процедурой ортогонального вращения. |
|
|
'varimax' |
Метод ортогонального вращения - варимакс. Значение 'rotate' по умолчанию. Вращение методом варимакс позволяет упростить столбцы матрицы lambda, сводя значения элементов к 1 или 0. Приведенные ниже дополнительные входные параметры 'normalize', 'reltol', 'maxit' позволяют управлять процедурой вращения методом варимакс. |
|
|
'procrustes' |
Косоугольное или ортогональное вращение для получения максимального соответствия матрицы нагрузок целевой матрице. Критерием соответствия является сумма квадратов отклонений коэффициентов целевой и рассчитанной матриц нагрузок. По умолчанию используется косоугольное вращение. Приведенные ниже дополнительные входные параметры 'typeprocr', 'targetprocr' предназначены для задания вида вращения и целевой матрицы нагрузок. |
|
|
'promax' |
Косоугольное вращение для получения матрицы нагрузок факторов приближенной к целевой матрице. Целевая матрица нагрузок рассчитывается функцией factoran с параметром 'rotate' равным 'orthomax'. Дополнительный входной параметр 'powerpm' задает степень целевой матрицы нагрузок. Поскольку factoran с параметром 'rotate'='orthomax' при расчете целевой матрицы нагрузок вызывается из основной функции, то допустимо использовать параметры 'coeffom', 'normalize', 'reltol', 'maxit'. |
|
|
Function |
Указатель на функцию вращения заданную в следующей форме [B,T] = myrotation(A,...) где A - исходная матрица нагрузок факторов, размерность A - d×m; B - матрица нагрузок после вращения, размерность B - d×m; T - матрица вращения с размерностью m×m. Для передачи входных аргументов функции вращения используется дополнительный параметр 'userargs'. |
|
|
'coeffom' |
Коэффициент ортогонального вращения. В литературе часто обозначается как |
|
|
'normalize' |
Нормализация по строкам матрицы нагрузок. Для 'normalize'=1 будет выполняться построчная нормализация значений элементов матрицы нагрузок. Для 'normalize'=0 нормализация не выполняется. 'normalize' используется для 'rotate'='orthomax', или 'rotate'='varimax'. Значение по умолчанию 'normalize'=1. |
|
|
'reltol' |
Предельное значение погрешности схождения алгоритма для методов ортогонального вращения 'orthomax' и 'varimax'. Значение по умолчанию sqrt(eps). |
|
|
'maxit' |
Максимальное число итераций при ортогональном вращении методами 'orthomax' и 'varimax'. Значение по умолчанию 250. |
|
|
'targetprocr' |
Целевая матрица нагрузок. Используется для 'rotate'='procrustes'. Значение по умолчанию отсутствует. |
|
|
'typeprocr' |
Вид вращения матрицы нагрузок для 'rotate'='procrustes'. Для 'typeprocr'='oblique' используется косоугольное вращение. Если 'typeprocr'='orthogonal' используется ортогональное вращение. Значение по умолчанию 'typeprocr'='oblique'. |
|
|
'powerpm' |
Степень целевой матрицы. Используется для 'rotate'='promax'. Значение 'powerpm' должно быть больше или равно 1. По умолчанию 'powerpm'=4. |
|
|
'userargs' |
Передача дополнительных входных параметров функции вращения заданной пользователем, 'rotate'=Function. Список передаваемых параметров формируется по правилу: первым параметром Function является матрица А, затем следует список переменных и констант функции factoran после входного параметра 'userargs'. |
|
|
'nobs' |
Число наблюдений многомерной случайной величины. Входной параметр 'nobs' используется, если Х задана как корреляционная или ковариационная матрица. Если Х задана как матрица наблюдений многомерной случайной величины, то 'nobs' игнорируется. Величина 'nobs' необходима для расчета уровня значимости при проверке нулевой гипотезы. Значение по умолчанию отсутствует. |
|
|
'delta' |
Минимальные значения дисперсий специфических факторов psi, используемые в процессе оптимизации методом максимального правдоподобия. Значение по умолчанию 0,005. |
|
|
'optimopts' |
Структура, определяющая параметры процедуры оптимизации методом максимального правдоподобия. Значение входного параметра 'optimopts' формируется при помощи функции optimset. Функция factoran использует следующие поля optimset: 'Display', 'MaxFunEvals', 'MaxIter', 'TolFun', 'TolX'. Значения полей структуры optimset по умолчанию: 'Display'='notify'; 'MaxFunEvals'=100*d; 'MaxIter'=400; 'TolFun'=1e-8; 'TolX'=1e-8. Примечание: в Statistics toolbox 4.1 структура, определяющая параметры процедуры оптимизации, формируется с помощью функции statset. Команда statset('factoran') позволяет получить список полей структуры, используемые функцией factoran, и их значения по умолчанию: >> statset('factoran') ans = Display: 'notify' MaxFunEvals: 400 MaxIter: 100 TolBnd: [] TolFun: 1.0000e-008 TolX: 1.0000e-008 |
|
Состав полей структуры параметров оптимизации алгоритма factoran и их назначение:
|
Поле структуры (параметр функции statset) |
Назначение |
Допустимые значения |
|
Display |
Отображение промежуточной информации о работе алгоритма оптимизации функции |
|
|
MaxFunEvals |
Максимальное количество вызовов целевой функции |
Положительное целое число |
|
MaxIter |
Максимальное количество итераций |
Положительное целое число |
|
TolBnd |
Ограничение на возможные значения оптимизируемого параметра |
Положительное вещественное число |
|
TolFun |
Значение выходного параметра функции при котором прекращается работа алгоритма оптимизации |
Положительное вещественное число |
|
TolX |
Значение параметров функции при котором прекращается работа алгоритма оптимизации |
Положительное вещественное число |
Примечания:
1. Признаки многомерной случайной величины Х, заданной как матрица наблюдений, должны быть линейно независимы, т.е. ранг матрицы ковариаций должен быть равен числу столбцов или строк cov(X). При соблюдении этого условия возможно использование метода максимального правдоподобия. Перед определением матрицы нагрузок lambda в factoran рассчитывается корреляционная матрица по Х, не зависимо от того, задана Х как матрица наблюдений или матрица ковариаций.
Перед расчетом матрицы нагрузок factoran стандартизует значения строк матрицы наблюдений Х. После стандартизации среднее наблюдений Х будет равно нулю, а дисперсия единице. Стандартизация Х не влияет на оценку матрицы нагрузок, поскольку метод максимального правдоподобия в рассматриваемой модели простого факторного анализа инвариантен к указанной операции. После стандартизации оценка корреляционной матрицы для исходных данных Х будет определяться из выражения lambda*lambda'+diag(psi). Приведенное выражение не распространяется на случай косоугольного вращения матрицы нагрузок.
2. Если элементы вектора psi приблизительно равны значению параметра 'delta', т.е. приблизительно равны нулю, то интерпретация результатов расчета может быть неоднозначной. Такая ситуация известна как случай Хейвуда. В частности, возможно наличие одного или нескольких локальных максимумов на функции максимального правдоподобия, каждый из которых соответствует различной оценке матрицы нагрузок и дисперсий специфических факторов. В частности случай Хейвуда может возникнуть при использовании большого или малого числа простых факторов.
3. Если явно не задано 'rotate'='none', factoran использует тот или иной алгоритм вращения матриц lambda и F. Выходная матрица Т используется в процедуре вращения нагрузок факторов согласно выражению lambda=lambda0*T, где lambda0 - начальная, полученная методом максимального правдоподобия, матрица нагрузок. Т является ортогональной матрицей для ортогонального вращения. Т является тождественной матрицей в случае 'rotate'='none'. Матрица обратная к Т называется матрицей вращения первичных осей. При ортогональном вращении эти две матрицы идентичны.
Матрица F рассчитывается из выражения F=F0*inv(T'), где F0 - матрица рассчитанных значений многомерной случайной величины не прошедшая процедуру вращения. Оценка матрицы ковариаций F определяется как inv(T'*T). Ковариационная матрица F при ортогональном вращении или отсутствии вращения является единичной матрицей. Вращение матриц lambda и F предназначено для получения более простых в интерпретации структур матриц, после расчета их оценок методом максимального правдоподобия.
Примеры использования функции простого факторного анализа
1. Расчет матрицы нагрузок lambda методом максимального правдоподобия для 5-ти простых факторов. Входной параметр Х является матрицей наблюдений 20-ти мерной случайной величины, распределенной по нормальному закону.
>> X=normrnd(0,1,100,20);
>> m=5;
>> lambda = factoran(X,m)
Warning: Some unique variances are zero.
> In C:\MATLAB6p5p1\toolbox\stats\factoran.m at line 404
lambda =
0.9829 0.1123 -0.0802 0.0652 0.0747
-0.0057 -0.0096 0.3288 0.1485 0.0774
-0.0112 0.0341 -0.0733 0.3250 -0.0899
0.0485 0.2711 0.1000 -0.0513 0.2824
-0.0263 0.1817 -0.0843 -0.7690 -0.1566
0.0231 -0.1078 -0.0684 0.2347 -0.3194
-0.1590 0.9695 -0.0479 -0.1605 0.0425
0.0781 -0.0675 -0.0385 -0.1241 -0.0699
-0.0364 0.0525 0.0420 -0.0307 0.1330
0.2283 0.1032 0.0157 0.0982 0.3688
-0.2977 0.0636 -0.1013 0.1479 -0.0153
0.0659 0.2323 -0.0239 0.1014 -0.0059
0.1727 0.0238 -0.1892 0.1537 -0.0367
0.1901 0.0485 0.9495 -0.1890 -0.1387
-0.0973 -0.0302 -0.1096 -0.1440 0.0574
0.0139 0.0807 -0.1854 -0.0469 0.2552
-0.0943 0.0623 -0.0539 0.2799 -0.2402
0.0713 -0.0783 -0.0674 0.1382 0.3928
-0.0456 -0.0080 0.0931 -0.0617 0.0772
0.1038 0.1305 -0.0201 0.0661 -0.5428
2. Расчет матрицы нагрузок lambda, вектора точечных оценок дисперсий специфических факторов psi, матрицы вращения нагрузок Т, структуры stats и рассчитанных по модели простого факторного анализа значений многомерной случайной величины F. Входной параметр Х является матрицей наблюдений 20-ти мерной случайной величины, распределенной по нормальному закону. Число простых факторов равно 5.
>> X=normrnd(1,5,25,20);
>> m=4;
>> [lambda,psi,T,stats,F] = factoran(X,m)
Warning: Some unique variances are zero: cannot compute significance.
> In C:\MATLAB6p5p1\toolbox\stats\factoran.m at line 401
lambda =
-0.2272 0.4192 -0.4739 0.3417
0.1212 -0.0065 0.0549 -0.2516
-0.0903 -0.1869 0.1857 0.1187
0.9257 -0.1448 0.2112 -0.2692
0.5325 0.1707 0.1262 0.8163
0.0350 -0.0875 0.4763 0.2756
0.1130 -0.0236 0.0749 -0.3685
-0.1037 0.5344 0.0439 -0.0627
0.4463 0.0699 -0.2298 0.0069
0.4420 0.0938 0.1206 0.3356
0.0530 -0.2685 0.0524 0.2999
0.3568 -0.1125 -0.0336 0.0124
-0.0051 -0.0242 0.0213 0.2672
0.3616 0.0110 0.0067 -0.0900
-0.3946 0.1139 0.0229 0.2877
-0.0892 -0.9898 -0.0237 -0.0823
-0.0975 0.2751 0.9539 -0.0018
-0.2801 0.4559 0.0778 0.2488
0.0416 0.0191 0.4228 -0.1782
-0.3241 0.1977 -0.1368 -0.1705
psi =
0.4312
0.9189
0.9083
0.0050
0.0050
0.6883
0.8453
0.6978
0.7431
0.6687
0.8324
0.8587
0.9275
0.8610
0.7480
0.0050
0.0050
0.6457
0.7874
0.8081
T =
0.8143 -0.5718 -0.0992 0.0062
0.4876 0.6107 0.5059 0.3652
-0.0814 -0.2587 0.7889 -0.5515
-0.3040 -0.4829 0.3345 0.7500
stats =
loglike: -6.8828
dfe: 116
F =
0.5485 -0.2866 -0.6313 0.9956
0.2492 0.1964 -1.2001 -0.7891
1.5662 1.1464 -0.5926 -0.9621
0.5558 1.4738 0.8657 -0.1663
-1.5837 0.9509 1.6995 0.8867
0.7672 -0.6756 1.3255 -1.9455
-0.3084 -1.6206 0.1266 -0.6515
1.2598 -0.7093 -0.1292 -1.3174
-0.4354 1.6870 -0.4330 -1.1354
-2.4350 0.4316 -0.7276 -0.8032
0.6997 1.2864 0.8787 0.1718
-0.1056 -1.5958 -0.3252 1.1452
-0.8290 0.2508 0.4989 -0.5693
0.5709 0.8002 -1.9973 1.8964
-0.8561 -0.8317 -0.0804 0.5780
0.7700 -0.4779 1.8274 1.1599
1.1085 -1.4129 0.1357 1.0528
-1.0208 -0.6924 -0.0406 0.2311
-0.6936 0.6774 -0.5940 -0.4581
0.6518 0.2537 -1.2641 1.1949
-0.4218 0.8697 0.4580 0.8158
-1.6916 -0.9387 0.0157 0.1253
0.4045 -1.4399 0.1097 -1.2267
0.8532 0.6800 1.6408 0.5918
0.3757 -0.0229 -1.5668 -0.8206
3. Анализ структуры 5-ти мерной случайной величины, характеризующей параметры автотранспортных средств. В качестве признаков многомерной случайной величины выступают: Acceleration - ускорение автотранспортного средства, Displacement - объем двигателя, Horsepower - мощность двигателя, MPG - расход топлива, Weight - масса автотранспортного средства.
3.1. Выполняется загрузка данных из файла carbig и расчет параметров модели простого факторного анализа для двух факторов. Расчет значений многомерной случайной величины F по модели (1) производится с использованием критерия минимума средней квадратической ошибки, 'scores'='regression'.
>> load carbig
>> X = [Acceleration Displacement Horsepower MPG Weight];
>> X = X(all(~isnan(X),2),:);
>> [Lambda,Psi,T,stats,F] = factoran(X,2,'scores','regression')
Lambda =
-0.2432 -0.8500
0.8773 0.3871
0.7618 0.5930
-0.7978 -0.2786
0.9692 0.2129
Psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
0.9476 0.3195
0.3195 -0.9476
stats =
loglike: -0.0030
dfe: 1
chisq: 1.1544
p: 0.2826
F =
0.4568 0.9158
0.5897 1.6438
0.2573 1.6383
0.3108 1.4154
0.2700 1.4815
…………………
-0.4972 -2.2391
-1.0830 0.9731
-0.2423 -0.9284
-0.0983 -1.1388
3.2. Расчет корреляционной матрицы для значений F. Корреляционная матрица должна быть равна eye(2).
>> inv(T'*T)
ans =
1 0
0 1
>> inv(T'*T)== eye(2)
ans =
1 1
1 1
3.3. Расчет корреляционной матрицы для матрицы исходных данных Х.
>> Lambda*Lambda' + diag(Psi)
ans =
1.0000 -0.5424 -0.6893 0.4309 -0.4167
-0.5424 1.0000 0.8979 -0.8078 0.9328
-0.6893 0.8979 1.0000 -0.7730 0.8647
0.4309 -0.8078 -0.7730 1.0000 -0.8326
-0.4167 0.9328 0.8647 -0.8326 1.0000
3.4. Расчет матрицы нагрузок полученной методом максимального правдоподобия до процедуры ортогонального вращения
>> Lambda*inv(T)
ans =
-0.5020 0.7277
0.9550 -0.0865
0.9113 -0.3185
-0.8450 0.0091
0.9865 0.1079
3.5. Расчет матрицы рассчитанных значений многомерной случайной величины, полученной методом максимального правдоподобия до процедуры ортогонального вращения
>> F*T'
ans =
0.7255 -0.7219
1.0840 -1.3692
0.7673 -1.4702
0.7467 -1.2419
0.7292 -1.3176
……………………………………………………
-0.3073 0.2295
-1.1865 1.9629
-0.7153 -1.2681
-0.5262 0.8023
-0.4570 1.0477
4. Анализ структуры 5-ти мерной случайной величины, характеризующей параметры автотранспортных средств. В качестве признаков многомерной случайной величины выступают: Acceleration - ускорение автотранспортного средства, Displacement - объем двигателя, Horsepower - мощность двигателя, MPG - расход топлива, Weight - масса автотранспортного средства. Выполняется загрузка данных из файла carbig и расчет параметров модели простого факторного анализа для двух факторов. В качестве входных значений используется ковариационная и корреляционная матрицы наблюдений Х, 'xtype'='cov'. В этом случае не могут быть рассчитаны матрица значений многомерной случайной величины F и уровень значимости.
>> load carbig
>> X = [Acceleration Displacement Horsepower MPG Weight];
>> X = X(all(~isnan(X),2),:);
>> [Lambda,Psi,T] = factoran(cov(X),2,'xtype','cov')
Lambda =
-0.2432 -0.8500
0.8773 0.3871
0.7618 0.5930
-0.7978 -0.2786
0.9692 0.2129
Psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
0.9476 0.3195
0.3195 -0.9476
В качестве исходных данных используется корреляционная матрица.
>> [Lambda,Psi,T] = factoran(corrcoef(X),2,'xtype','cov')
Lambda =
-0.2432 -0.8500
0.8773 0.3871
0.7618 0.5930
-0.7978 -0.2786
0.9692 0.2129
Psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
0.9476 0.3195
0.3195 -0.9476
5. Анализ структуры 5-ти мерной случайной величины, характеризующей параметры автотранспортных средств. В качестве признаков многомерной случайной величины выступают: Acceleration - ускорение автотранспортного средства, Displacement - объем двигателя, Horsepower - мощность двигателя, MPG - расход топлива, Weight - масса автотранспортного средства.
5.1. Выполняется загрузка данных из файла carbig и расчет параметров модели простого факторного анализа для двух факторов. В качестве метода вращения используется косоугольное вращение, 'rotate'='promax', для получения матрицы нагрузок факторов приближенной к целевой матрице нагрузок. Степень целевой матрицы, 'powerpm', равна 4.
>> load carbig
>> X = [Acceleration Displacement Horsepower MPG Weight];
>> X = X(all(~isnan(X),2),:);
>> [Lambda,Psi,T,stats,F] = factoran(X,2,'rotate','promax','powerpm',4)
Lambda =
0.0964 0.9426
0.8879 -0.1057
0.6526 -0.4076
-0.8413 0.0059
1.0800 0.1472
Psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
1.0045 0.0070
0.8254 1.3001
stats =
loglike: -0.0030
dfe: 1
chisq: 1.1544
p: 0.2826
F =
0.7381 -1.1402
1.1048 -1.9752
0.7853 -1.8663
0.7630 -1.6397
0.7458 -1.6992
……………………………………………………
-0.3121 0.4117
-1.2123 2.5957
-0.7148 -0.7258
-0.5372 1.0875
-0.4689 1.2723
5.2. Расчет корреляционной матрицы для значений F. Корреляционная матрица не должна быть равна eye(2).
>> inv(T'*T)
ans =
1.0000 -0.6391
-0.6391 1.0000
>> inv(T'*T)== eye(2)
ans =
0 0
0 0
5.3. Расчет корреляционной матрицы для матрицы исходных данных Х.
>> Lambda*inv(T'*T)*Lambda' + diag(Psi)
ans =
1.0000 -0.5424 -0.6893 0.4309 -0.4167
-0.5424 1.0000 0.8979 -0.8078 0.9328
-0.6893 0.8979 1.0000 -0.7730 0.8647
0.4309 -0.8078 -0.7730 1.0000 -0.8326
-0.4167 0.9328 0.8647 -0.8326 1.0000
5.4. Графическое представление результатов простого факторного анализа после косоугольного вращения матрицы нагрузок.
>> invT = inv(T)
invT =
1.0000 -0.0054
-0.6349 0.7726
>> Lambda0 = Lambda*invT
Lambda0 =
-0.5020 0.7277
0.9550 -0.0865
0.9113 -0.3185
-0.8450 0.0091
0.9865 0.1079
>> plot(Lambda0(:,1),Lambda0(:,2), 'ro');
>> line([-invT(1,1) invT(1,1) NaN -invT(2,1) invT(2,1)],[-invT(1,2) invT(1,2) NaN -invT(2,2) invT(2,2)]);
>> text(invT(:,1), invT(:,2),[' I '; ' II']);
>> xlabel('Loadings for unrotated Factor 1')
>> ylabel('Loadings for unrotated Factor 2')
6. Использование функции вращения заданной пользователем. Функция пользователя реализует косоугольное вращение. Дополнительными параметрами функции вращения являются целевая матрица нагрузок и число простых факторов.
6.1. Текст функции вращения myrotation:
function [B, T] = myrotation (A, Target,m)
% Косоугольное вращение
% Входные параметры:
% A - матрица нагрузок до вращения;
% Target - целевая матрица нагрузок;
% m - число простых факторов.
% Выходные параметры:
% B - матрица нагрузок после вращения;
% T - матрица вращения.
T = A \ Target;
T = T * diag(sqrt(diag((T'*T)\eye(m))));
B = A * T;
6.2. Выполняется загрузка данных из файла carbig и расчет параметров модели простого факторного анализа для двух факторов.
>> load carbig
>> X = [Acceleration Displacement Horsepower MPG Weight];
>> X = X(all(~isnan(X),2),:);
>> Target= factoran(X,2).^2;
>> [Lambda,Psi,T]=factoran(X,2,'rotate',@myrotation,'userargs', Target,2)
Lambda =
-0.0157 0.8729
1.0582 0.1476
0.8229 -0.1878
-0.9897 -0.2246
1.2493 0.4273
Psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
1.1798 0.2808
0.7923 1.3931
7. Анализ структуры 5-ти мерной случайной величины для двух факторов. В качестве метода вращения используется ортогональное вращение с коэффициентом ![]() .
.
>> load carbig
>> X = [Acceleration Displacement Horsepower MPG Weight];
>> X = X(all(~isnan(X),2),:);
>> [Lambda,Psi,T]=factoran(X,2, 'coeffom', 0.5)
Lambda =
-0.2432 -0.8500
0.8773 0.3871
0.7618 0.5930
-0.7978 -0.2786
0.9692 0.2129
Psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
0.9476 0.3195
0.3195 -0.9476
8. Анализ структуры 5-ти мерной случайной величины для двух факторов. В качестве метода вращения используется ортогональное вращение с коэффициентом ![]() . Входные данные заданы в виде ковариационной матрицы. Для расчета полей структуры stats: stats.chisq и stats.p, задан дополнительный входной параметр 'nobs'=100.
. Входные данные заданы в виде ковариационной матрицы. Для расчета полей структуры stats: stats.chisq и stats.p, задан дополнительный входной параметр 'nobs'=100.
>> load carbig
>> X = [Acceleration Displacement Horsepower MPG Weight];
>> X = X(all(~isnan(X),2),:);
>> С= cov(X)
C =
1.0e+005 *
0.0001 -0.0016 -0.0007 0.0001 -0.0098
-0.0016 0.1095 0.0361 -0.0066 0.8293
-0.0007 0.0361 0.0148 -0.0023 0.2827
0.0001 -0.0066 -0.0023 0.0006 -0.0552
-0.0098 0.8293 0.2827 -0.0552 7.2148
>> [lambda,psi,T,stats] = factoran(C,2,'xtype','cov', 'nobs', 100)
lambda =
-0.2432 -0.8500
0.8773 0.3871
0.7618 0.5930
-0.7978 -0.2786
0.9692 0.2129
psi =
0.2184
0.0804
0.0680
0.2859
0.0152
T =
0.9476 0.3195
0.3195 -0.9476
stats =
loglike: -0.0030
dfe: 1
chisq: 0.2838
p: 0.5943
pcacov - Функция служит для реализации метода главных компонент по заданной в качестве входного параметра матрице ковариаций
Синтаксис
pc = pcacov(X)
[pc,latent,explained] = pcacov(X)
Описание
pc = pcacov(X) функция позволяет провести анализ главных компонент на основе ковариационной матрицы Х исходных данных. Функция возвращает матрицу главных компонент pc. Матрица pc является множеством собственных векторов ковариационной матрицы Х. Размерности матриц pc и Х будет одинаковой.
[pc,latent,explained] = pcacov(X) функция возвращает матрицу главных компонент pc, вектор собственных значений ковариационной матрицы latent, вектор долей explained, в процентах, от общей дисперсии, объясняемых собственными векторами (главными компонентами). Число элементов векторов latent и explained равно количеству столбцов или строк Х.
Примеры использования функции анализа главных компонент по ковариационной матрице
Анализ главных компонент 10-ти мерной случайной величины, распределенной по стандартизованному нормальному закону. Функция возвращает матрицу главных компонент.
>> x=normrnd(0,1,100,10);
>> covx = cov(x)
covx =
1.2405 -0.0065 -0.0939 -0.0235 -0.0983 -0.0210 0.0922 0.0705 -0.1096 0.1389
-0.0065 1.0529 0.0592 -0.0741 -0.0616 0.0173 0.0615 -0.0285 0.1016 0.0593
-0.0939 0.0592 0.9317 0.0611 0.1394 0.0672 -0.2186 0.0323 -0.0338 -0.0160
-0.0235 -0.0741 0.0611 1.3267 -0.0913 0.0326 -0.1315 0.0585 0.0949 -0.1333
-0.0983 -0.0616 0.1394 -0.0913 0.8328 0.0067 -0.0682 0.0525 0.0011 0.0839
-0.0210 0.0173 0.0672 0.0326 0.0067 1.2301 -0.0447 0.1030 0.1220 -0.0342
0.0922 0.0615 -0.2186 -0.1315 -0.0682 -0.0447 1.1526 -0.2048 -0.0090 0.0227
0.0705 -0.0285 0.0323 0.0585 0.0525 0.1030 -0.2048 0.8355 -0.1004 0.1387
-0.1096 0.1016 -0.0338 0.0949 0.0011 0.1220 -0.0090 -0.1004 0.9864 -0.1950
0.1389 0.0593 -0.0160 -0.1333 0.0839 -0.0342 0.0227 0.1387 -0.1950 0.9568
>> pc = pcacov(covx)
pc =
-0.3971 -0.3129 -0.5431 0.3598 -0.1318 0.4485 -0.2956 0.0843 0.0247 0.0805
-0.0737 0.1629 0.2012 0.2575 -0.8491 -0.1267 0.1124 -0.1050 0.1873 0.2561
0.2808 -0.2452 0.2390 -0.0494 -0.2525 0.0157 -0.6790 -0.2254 -0.0772 -0.4688
0.5471 0.0422 -0.6846 -0.0823 -0.1610 -0.4002 -0.0936 0.1116 -0.0257 0.1248
0.0610 -0.1892 0.3025 -0.1004 0.1026 -0.0824 -0.4032 0.5846 0.3036 0.4951
0.2918 -0.0401 0.1603 0.8377 0.3206 -0.1649 -0.0303 -0.1544 -0.0996 0.1455
-0.4653 0.4827 -0.1139 0.1398 0.1389 -0.4824 -0.3362 0.0693 0.2596 -0.2841
0.1001 -0.4344 -0.0307 0.1242 -0.0021 -0.1029 0.3551 0.1420 0.6620 -0.4356
0.2543 0.4294 0.0480 0.2098 -0.1298 0.3754 0.0666 0.6256 -0.1435 -0.3611
-0.2805 -0.4126 0.0740 0.0654 -0.1502 -0.4520 0.1524 0.3696 -0.5738 -0.1595
Анализ главных компонент 4-х мерной случайной величины. Функция возвращает матрицу главных компонент, собственные значения ковариационной матрицы, вектор долей от общей дисперсии, объясняемых главными компонентами.
>> load hald
>> covx = cov(ingredients)
covx =
34.6026 20.9231 -31.0513 -24.1667
20.9231 242.1410 -13.8782 -253.4167
-31.0513 -13.8782 41.0256 3.1667
-24.1667 -253.4167 3.1667 280.1667
>> [pc,variances,explained] = pcacov(covx)
pc =
-0.0678 0.6460 -0.5673 0.5062
-0.6785 0.0200 0.5440 0.4933
0.0290 -0.7553 -0.4036 0.5156
0.7309 0.1085 0.4684 0.4844
variances =
517.7969
67.4964
12.4054
0.2372
explained =
86.5974
11.2882
2.0747
0.0397
pcares - Функция служит для определения остатка после удаления заданного количества главных компонент
Синтаксис
residuals = pcares(X,ndim)
Описание
residuals = pcares(X,ndim) функция возвращает матрицу остатков residuals по ndim главным компонентам. Входной параметр Х является матрицей исходных данных. Столбцы матрицы Х соответствуют признакам, строки - наблюдениям многомерной случайной величины. Входной параметр ndim должен быть задан как скаляр. Величина ndim должна быть меньше числа столбцов матрицы Х. Размерность матриц residuals и Х будет одинаковой.
Примечание: Матрица Х должна быть задана как матрица исходных данных, а не ковариационная матрица.
Примеры использования функции расчета остатков главных компонент
Расчет остатков по 5-ти главным компонентам для 10-ти мерной случайной величины, распределенной по стандартизованному нормальному закону. Объем выборки равен 20 элементам.
>> x=normrnd(0,1,20,10)
x =
-0.4326 0.2944 -1.6041 0.0000 0.6232 -1.1878 0.1286 -0.3306 0.4694 -0.4650
-1.6656 -1.3362 0.2573 -0.3179 0.7990 -2.2023 0.6565 -0.8436 -0.9036 0.3710
0.1253 0.7143 -1.0565 1.0950 0.9409 0.9863 -1.1678 0.4978 0.0359 0.7283
0.2877 1.6236 1.4151 -1.8740 -0.9921 -0.5186 -0.4606 1.4885 -0.6275 2.1122
-1.1465 -0.6918 -0.8051 0.4282 0.2120 0.3274 -0.2624 -0.5465 0.5354 -1.3573
1.1909 0.8580 0.5287 0.8956 0.2379 0.2341 -1.2132 -0.8468 0.5529 -1.0226
1.1892 1.2540 0.2193 0.7310 -1.0078 0.0215 -1.3194 -0.2463 -0.2037 1.0378
-0.0376 -1.5937 -0.9219 0.5779 -0.7420 -1.0039 0.9312 0.6630 -2.0543 -0.3898
0.3273 -1.4410 -2.1707 0.0403 1.0823 -0.9471 0.0112 -0.8542 0.1326 -1.3813
0.1746 0.5711 -0.0592 0.6771 -0.1315 -0.3744 -0.6451 -1.2013 1.5929 0.3155
-0.1867 -0.3999 -1.0106 0.5689 0.3899 -1.1859 0.8057 -0.1199 1.0184 1.5532
0.7258 0.6900 0.6145 -0.2556 0.0880 -1.0559 0.2316 -0.0653 -1.5804 0.7079
-0.5883 0.8156 0.5077 -0.3775 -0.6355 1.4725 -0.9898 0.4853 -0.0787 1.9574
2.1832 0.7119 1.6924 -0.2959 -0.5596 0.0557 1.3396 -0.5955 -0.6817 0.5045
-0.1364 1.2902 0.5913 -1.4751 0.4437 -1.2173 0.2895 -0.1497 -1.0246 1.8645
0.1139 0.6686 -0.6436 -0.2340 -0.9499 -0.0412 1.4789 -0.4348 -1.2344 -0.3398
1.0668 1.1908 0.3803 0.1184 0.7812 -1.1283 1.1380 -0.0793 0.2888 -1.1398
0.0593 -1.2025 -1.0091 0.3148 0.5690 -1.3493 -0.6841 1.5352 -0.4293 -0.2111
-0.0956 -0.0198 -0.0195 1.4435 -0.8217 -0.2611 -1.2919 -0.6065 0.0558 1.1902
-0.8323 -0.1567 -0.0482 -0.3510 -0.2656 0.9535 -0.0729 -1.3474 -0.3679 -1.1162
>> ndim=5;
>> residuals = pcares(x,ndim)
residuals =
-0.1294 0.6677 -0.6751 -0.3242 -0.1797 -0.0065 0.0548 0.2045 -0.0302 -0.2121
-0.0909 -0.4201 0.8606 0.6110 0.1447 -0.3791 -0.4141 -0.3849 -0.3067 0.0446
-0.1012 0.4955 -0.3300 0.0417 1.0371 0.6236 0.3302 0.2182 -0.4122 0.0977
-0.0515 0.1014 -0.0164 -0.7937 -0.2165 -0.0626 -0.3016 0.6726 0.4219 -0.6217
-0.1767 0.0343 0.2418 -0.1249 0.0220 0.0448 0.0363 0.5205 0.2709 -0.3250
-0.0797 -0.1271 0.5396 -0.0536 0.2450 -0.2728 -0.6093 0.0055 -0.2204 -0.3225
0.0420 0.0629 -0.1499 0.1606 -0.4859 -0.4537 -0.2870 -0.5388 -0.2187 0.1063
-0.0454 -0.1224 0.0969 0.3801 -0.3616 -0.1424 0.2100 -0.1590 0.1155 0.1813
0.5051 -0.2070 -0.4844 -0.8277 0.1865 0.2268 -0.3044 -0.2563 -0.0737 0.1138
0.0541 -0.2823 0.1097 0.2053 -0.6232 -0.2698 0.0750 -0.2121 0.2462 0.1430
0.1628 -0.3271 -0.2793 0.4703 -0.4444 0.3633 1.0214 -0.1356 0.4788 0.6807
-0.0363 0.1308 0.1033 0.1934 0.3557 -0.1542 -0.3707 -0.3575 -0.5211 0.0221
0.0737 -0.0987 -0.0569 -0.1726 0.2851 0.4141 0.3308 0.3130 0.2152 0.0564
0.3496 -0.8068 0.2989 0.1823 0.0402 0.3136 0.3845 -0.2259 0.2907 0.5144
0.0732 0.3262 -0.3490 -0.2363 0.4463 0.0822 -0.2788 -0.2058 -0.4617 -0.0103
-0.1208 0.6681 -0.9128 0.1204 -0.4478 0.1010 0.6148 -0.0049 0.0689 0.2048
-0.3961 0.4129 0.1490 0.0509 0.2484 0.1323 0.1825 0.6987 0.1302 -0.4058
-0.0651 -0.1566 0.4483 -0.4509 0.2001 -0.0108 -0.3704 0.5345 0.2151 -0.5037
-0.0287 -0.3294 0.3863 0.8357 -0.6222 -0.5818 -0.0922 -0.7531 -0.1630 0.3643
0.0615 -0.0223 0.0194 -0.2681 0.1704 0.0319 -0.2119 0.0663 -0.0457 -0.1283
Расчет остатков по 1, 2, 3 главным компонентам для 4-х мерной случайной величины. Объем выборки равен 13 элементам.
>> load hald
>> ingredients
ingredients =
7 26 6 60
1 29 15 52
11 56 8 20
11 31 8 47
7 52 6 33
11 55 9 22
3 71 17 6
1 31 22 44
2 54 18 22
21 47 4 26
1 40 23 34
11 66 9 12
10 68 8 12
>> r1 = pcares(ingredients,1)
r1 =
2.0350 2.8304 -6.8378 3.0879
-4.4542 0.9352 2.3715 0.3608
2.6583 -0.9622 -3.3925 -0.5120
5.1463 -1.0630 -4.4575 -0.3325
-0.4990 3.4708 -5.7532 3.4043
2.8054 -0.4903 -2.4554 -0.0974
-6.6710 0.7346 6.1765 -0.1822
-4.9288 -1.8150 9.5747 -2.5224
-6.0895 -0.4387 6.4996 -1.2302
13.3158 -3.3821 -7.6739 -1.5998
-5.8364 -1.8979 10.9632 -2.7387
1.8038 0.4864 -2.0267 0.6993
0.7144 1.5919 -2.9885 1.6628
>> r2 = pcares(ingredients,2)
r2 =
-2.4037 2.6930 -1.6482 2.3425
-1.4755 1.0274 -1.1111 0.8610
-0.0582 -1.0463 -0.2165 -0.9681
0.8606 -1.1957 0.5533 -1.0521
-3.3814 3.3816 -2.3832 2.9203
0.4496 -0.5632 0.2988 -0.4930
-0.8699 0.9141 -0.6061 0.7920
2.0003 -1.6006 1.4733 -1.3589
-0.2848 -0.2590 -0.2872 -0.2555
4.1699 -3.6651 3.0192 -3.1356
2.1652 -1.6503 1.6079 -1.3950
0.0068 0.4308 0.0743 0.3976
-1.1790 1.5333 -0.7747 1.3449
>> r3 = pcares(ingredients,3)
r3 =
0.2008 0.1957 0.2045 0.1921
-0.2004 -0.1953 -0.2041 -0.1918
-0.5700 -0.5555 -0.5806 -0.5455
-0.1916 -0.1867 -0.1952 -0.1834
0.0721 0.0702 0.0734 0.0690
-0.0683 -0.0666 -0.0696 -0.0654
0.0414 0.0403 0.0422 0.0396
0.1642 0.1600 0.1672 0.1571
-0.2752 -0.2682 -0.2803 -0.2634
0.1724 0.1680 0.1756 0.1649
0.2203 0.2146 0.2244 0.2108
0.2262 0.2204 0.2304 0.2164
0.2083 0.2030 0.2122 0.1994
princomp - Функция служит для реализации метода главных компонент по заданной в качестве входного параметра матрице исходных значений
Синтаксис
PC = princomp(X)
[PC,SCORE,latent,tsquare] = princomp(X)
Описание
PC = princomp(X) функция предназначена для проведения анализа главных компонент многомерной случайной величины Х. Входной параметр Х является матрицей исходных данных. Столбцы матрицы Х соответствуют признакам, строки - наблюдениям многомерной случайной величины. Функция возвращает матрицу главных компонент PC. Матрица PC является множеством собственных векторов ковариационной матрицы cov(Х). Размерность матрицы PC будет равна n?n, где n - количество признаков многомерной случайной величины, или число столбцов матрицы Х.
Примечание: Входной параметр Х должен быть задан как матрица исходных данных, а не ковариационная матрица.
[PC,SCORE,latent,tsquare] = princomp(X) функция возвращает матрицу главных компонент PC, матрицу Z-множества данных SCORE, собственные значения latent ковариационной матрицы cov(X), вектор значений статистики T2Хоттелинга tsquare для каждого из наблюдений.
Z-множество данных формируется проецированием матрицы наблюдений Х в пространство главных компонент. Элементы вектора latent являются дисперсиями столбцов матрицы SCORE. Статистика T2 Хоттелинга является мерой расстояния в многомерном пространстве отдельных наблюдений относительно центра группирования исходных данных.
Примеры использования функции анализа главных компонент
Анализ главных компонент 10-ти мерной случайной величины, распределенной по стандартизованному нормальному закону. Объем выборки равен 20 наблюдениям. Функция возвращает матрицу главных компонент.
>> x=normrnd(0,1,20,10)
x =
0.6353 -1.0181 0.4855 -0.5412 1.0641 -0.8960 0.8369 -0.6547 -0.9812 1.0821
-0.6014 -0.1821 -0.0050 -1.3335 -0.2454 0.1352 -0.7223 -1.0807 -0.6885 2.3726
0.5512 1.5210 -0.2762 1.0727 -1.5175 -0.1390 -0.7215 -0.0477 1.3395 0.2293
-1.0998 -0.0384 1.2765 -0.7121 0.0097 -1.1634 -0.2012 0.3793 -0.9092 -0.2666
0.0860 1.2274 1.8634 -0.0113 0.0714 1.1837 -0.0205 -0.3304 -0.4129 0.7017
-2.0046 -0.6962 -0.5226 -0.0008 0.3165 -0.0154 0.2789 -0.4999 -0.5062 -0.4876
-0.4931 0.0075 0.1034 -0.2494 0.4998 0.5362 1.0583 -0.0360 1.6197 1.8625
0.4620 -0.7829 -0.8076 0.3966 1.2781 -0.7164 0.6217 -0.1748 0.0809 1.1069
-0.3210 0.5869 0.6804 -0.2640 -0.5478 -0.6556 -1.7506 -0.9573 -1.0811 -1.2276
1.2366 -0.2512 -2.3646 -1.6640 0.2608 0.3144 0.6973 1.2925 -1.1245 -0.6699
-0.6313 0.4801 0.9901 -1.0290 -0.0132 0.1068 0.8115 0.4409 1.7357 1.3409
-2.3252 0.6682 0.2189 0.2431 -0.5803 1.8482 0.6363 1.2809 1.9375 0.3881
-1.2316 -0.0783 0.2617 -1.2566 2.1363 -0.2751 1.3101 -0.4977 1.6351 0.3931
1.0556 0.8892 1.2134 -0.3472 -0.2576 2.2126 0.3271 -1.1187 -1.2559 -1.7073
-0.1132 2.3093 -0.2747 -0.9414 -1.4095 1.5085 -0.6730 0.8076 -0.2135 0.2279
0.3792 0.5246 -0.1331 -1.1746 1.7701 -1.9451 -0.1493 0.0412 -0.1989 0.6856
0.9442 -0.0118 -1.2705 -1.0211 0.3255 -1.6805 -2.4490 -0.7562 0.3075 -0.6368
-2.1204 0.9131 -1.6636 -0.4017 -1.1190 -0.5735 0.4733 -0.0891 -0.5723 -1.0026
-0.6447 0.0559 -0.7036 0.1737 0.6204 -0.1858 0.1169 -2.0089 -0.9776 -0.1856
-0.7043 -1.1071 0.2809 -0.1161 1.2698 0.0089 -0.5911 1.0839 -0.4468 -1.0540
>> PC = princomp(x)
PC =
-0.3218 -0.1082 0.4495 -0.4540 0.5667 -0.1679 0.2817 -0.0781 0.1133 0.1701
0.2718 -0.3840 0.0631 -0.3077 -0.0340 0.0097 -0.0583 0.5278 0.3750 -0.5061
0.2531 -0.0023 0.7004 0.2568 -0.3186 -0.4228 -0.2063 -0.0370 0.1517 0.1797
0.1232 -0.0972 0.0171 0.0834 -0.2291 0.0454 0.6158 -0.5732 0.3092 -0.3320
-0.2522 0.5340 0.1372 0.2450 0.1297 -0.2926 0.1573 0.2350 -0.1845 -0.5966
0.5076 -0.3080 0.1803 0.2754 0.4406 0.1423 0.1010 -0.0599 -0.5399 -0.1396
0.2719 0.3465 -0.0443 0.3753 0.4122 0.2402 0.1122 0.1963 0.5712 0.2412
0.2197 0.0219 -0.3612 -0.0834 0.3464 -0.5508 -0.4074 -0.4046 0.1806 -0.1679
0.4858 0.3135 -0.1869 -0.3889 -0.1491 -0.3335 0.4299 0.2191 -0.2051 0.2668
0.2526 0.4822 0.2908 -0.4375 -0.0249 0.4612 -0.3115 -0.2765 -0.0387 -0.1986
Анализ главных компонент 4-х мерной случайной величины. Функция возвращает матрицу главных компонент, матрицу Z-множества данных, собственные значения ковариационной матрицы cov(X), вектор значений статистики T2Хоттелинга для каждого из наблюдений.
>> load hald;
>> ingredients
ingredients =
7 26 6 60
1 29 15 52
11 56 8 20
11 31 8 47
7 52 6 33
11 55 9 22
3 71 17 6
1 31 22 44
2 54 18 22
21 47 4 26
1 40 23 34
11 66 9 12
10 68 8 12
>> [pc,score,latent,tsquare] = princomp(ingredients)
pc =
0.0678 0.6460 -0.5673 0.5062
0.6785 0.0200 0.5440 0.4933
-0.0290 -0.7553 -0.4036 0.5156
-0.7309 0.1085 0.4684 0.4844
score =
-36.8218 6.8709 4.5909 0.3967
-29.6073 -4.6109 2.2476 -0.3958
12.9818 4.2049 -0.9022 -1.1261
-23.7147 6.6341 -1.8547 -0.3786
0.5532 4.4617 6.0874 0.1424
10.8125 3.6466 -0.9130 -0.1350
32.5882 -8.9798 1.6063 0.0818
-22.6064 -10.7259 -3.2365 0.3243
9.2626 -8.9854 0.0169 -0.5437
3.2840 14.1573 -7.0465 0.3405
-9.2200 -12.3861 -3.4283 0.4352
25.5849 2.7817 0.3867 0.4468
26.9032 2.9310 2.4455 0.4116
latent =
517.7969
67.4964
12.4054
0.2372
tsquare =
5.6803
3.0758
6.0002
2.6198
3.3681
0.5668
3.4818
3.9794
2.6086
7.4818
4.1830
2.2327
2.7216
barttest - Тест Бартлета
Синтаксис
ndim = barttest(x,alpha)
[ndim,prob,chisquare] = barttest(x,alpha)
Описание
ndim = barttest(x,alpha) функция позволяет оценить размерность ndim пространства главных компонент необходимого для того, чтобы объяснить неслучайные изменения в матрице исходных данных х при заданном уровне значимости alpha. Величина размерности ndim определяется в результате проверки последовательности нулевых гипотез. Нулевая гипотеза для ndim=1 состоит в том, что дисперсии исходных данных по всем главным компонентам равны. Нулевая гипотеза для ndim=2 состоит в том, что дисперсии исходных данных по второму и последующим главным компонентам равны. И так далее.
[ndim,prob,chisquare] = barttest(x,alpha) функция возвращает размерность пространства главных компонент ndim, объясняющих неслучайные изменения в матрице входных данных x, вектор уровней значимости prob, полученный при проверке последовательности нулевых гипотез о равенстве ndim заданному значению, вектор значений статистики хи-квадрат chisquare, использованных при проверке каждой из серии нулевых гипотез.
Примеры использования функции теста Бартлетта для оценки размерности пространства главных компонент
Тест Бартлетта для проверки нулевой гипотезы о величине размерности пространства главных компонент. В качестве исходных данных выступает матрица, состоящая из 3-х двумерных случайных величин, распределенных по многомерному нормальному закону с ковариационной матрицей [1 0.99; 0.99 1] и нулевым математическим ожиданием. Объем выборки 20 элементов. Функция возвращает размерность пространства главных компонент. Проверка гипотез проводится для уровня значимости 0,05.
>> x = mvnrnd([0 0],[1 0.99; 0.99 1],20);
>> x(:,3:4) = mvnrnd([0 0],[1 0.99; 0.99 1],20);
>> x(:,5:6) = mvnrnd([0 0],[1 0.99; 0.99 1],20)
x =
-0.5108 -0.5913 0.7582 0.5571 0.7599 0.7804
0.2349 0.3295 -0.6919 -0.7818 -1.7129 -1.6594
-0.5978 -0.5890 0.6802 0.7202 1.5370 1.8152
0.0208 0.1706 -1.0725 -1.2026 -1.6098 -1.9150
0.4194 0.2261 0.8998 0.9319 1.1095 1.1463
1.1911 1.2468 -2.1231 -1.9457 -1.1097 -1.0577
0.7712 0.5330 0.2847 0.3164 0.3855 0.4750
-2.6442 -2.8213 -0.7333 -0.7027 0.9652 0.8736
0.2854 0.3240 -0.7734 -0.7083 0.8183 0.9353
0.8261 0.7980 0.1518 0.3219 0.0370 0.0609
-0.0081 -0.1675 -0.3368 -0.1291 -0.9260 -0.7970
0.8584 0.8086 0.9708 0.8164 -0.1119 0.0252
0.7748 0.6849 -0.1072 -0.0772 -0.8030 -0.6085
1.3059 1.1664 1.0135 1.0864 -1.6650 -1.6574
1.2315 1.2543 -0.4753 -0.5078 -0.9014 -0.7066
0.9586 0.7388 0.0689 0.4203 0.5883 0.6146
-1.6545 -1.5938 0.3986 0.5154 0.5542 0.3469
-0.9904 -1.2662 1.1163 0.9851 -0.4152 -0.4321
0.6852 0.7530 0.6205 0.7288 0.0618 -0.0101
-0.9749 -0.9167 -0.2877 -0.1860 0.4574 0.2089
>> alpha=0.05;
>> ndim = barttest(x,alpha)
ndim =
3
Тест Бартлетта для проверки нулевой гипотезы о величине размерности пространства главных компонент. В качестве исходных данных выступает матрица, состоящая из 3-х двумерных случайных величин, распределенных по многомерному нормальному закону с ковариационной матрицей [1 0.8; 0.8 1] и нулевым математическим ожиданием. Объем выборки 20 элементов. Функция возвращает размерность пространства главных компонент, вектор уровней значимости, полученный при проверке серии нулевых гипотез, вектор значений статистики хи-квадрат, использованной при проверке каждой из серии нулевых гипотез. Проверка гипотез проводится для уровня значимости 0,01.
>> x = mvnrnd([0 0],[1 0.8; 0.8 1],20);
>> x(:,3:4) = mvnrnd([0 0],[1 0.8; 0.8 1],20);
>> x(:,5:6) = mvnrnd([0 0],[1 0.8; 0.8 1],20)
x =
-0.4175 -0.0695 -1.6466 -1.8292 -1.0082 -0.5103
-0.6150 -0.1527 0.4287 0.5503 -0.6646 -1.0542
0.7208 0.1604 -0.7372 -0.5239 0.5582 0.4944
0.3394 0.7718 0.5649 -0.2279 -1.1885 -1.2638
0.8828 -0.6362 -1.3842 -1.5172 -0.7755 -1.4687
0.2842 0.8860 0.4603 0.2015 0.2710 -0.0137
-0.1455 -0.1174 0.6294 0.8964 1.5350 0.9532
-0.0896 -1.0405 0.3798 -0.4452 -1.0523 -1.0167
0.2892 -0.5059 -1.0133 -1.1692 0.6256 0.3197
1.1648 1.0563 -0.3472 -0.5669 -0.7976 -1.5913
0.8057 0.7771 0.4419 0.9436 -0.3135 0.4058
-1.3556 -1.6882 -1.5902 -0.2149 -0.6022 0.3127
0.1209 -0.1751 -0.7014 0.2953 1.2591 0.9314
-0.2222 0.6619 -1.0776 -0.3150 0.8585 0.2445
0.5717 0.1802 1.0022 0.9979 -2.1053 -1.5560
-0.3001 -0.2205 1.7295 1.4254 -0.3609 -0.5291
1.1343 1.3867 0.7090 -0.3326 0.5536 0.4818
-0.1794 0.3946 -0.7479 -0.8493 -1.5564 -2.2999
-1.4671 -1.0909 0.2289 0.1705 -0.2067 0.8467
1.3953 0.1448 -0.2235 -0.0417 -0.4256 -0.1440
>> [ndim,prob,chisquare] = barttest(x,0.01)
ndim =
3
prob =
0.0000
0.0000
0.0001
0.8594
0.9756
chisquare =
64.8186
52.6410
33.1329
1.9249
0.0493
treedisp - Отображает граф возможных решений
Синтаксис
treedisp(T)
treedisp(T,'param1',val1,'param2',val2,...)
Описание
treedisp(T) функция позволяет получить графическое представление иерархической нелинейной регрессионной модели или бинарного дерева для классификации наблюдений на основе входного аргумента T. Параметр Т определяет вид дерева решений и задается как структура. Т является выходным аргументом функции treefit. Результат отображается в графическом окне (рис. 1). Промежуточные узлы дерева решений отмечены метками ![]() с условиями выбора относительно значения какой либо независимой переменной. Каждый из конечных узлов дерева решений имеет метку
с условиями выбора относительно значения какой либо независимой переменной. Каждый из конечных узлов дерева решений имеет метку ![]() со значением зависимой переменной. Для выбора одной из двух возможных ветвей дерева решений исходящих из промежуточного узла действует правило: левая ветвь соответствует выполнению условия относительно независимой переменной, правая - невыполнению этого условия. Определение значения зависимой переменной начинается с первого промежуточного узла, далее следуя заданному условию выбирается правая или левая исходящая ветвь. Аналогично просматриваются последующие узлы до тех пор пока не будет достигнут последний конечный узел. Числовая или категориальная метка, соответствующая последнему узлу, является значением зависимой переменной.
со значением зависимой переменной. Для выбора одной из двух возможных ветвей дерева решений исходящих из промежуточного узла действует правило: левая ветвь соответствует выполнению условия относительно независимой переменной, правая - невыполнению этого условия. Определение значения зависимой переменной начинается с первого промежуточного узла, далее следуя заданному условию выбирается правая или левая исходящая ветвь. Аналогично просматриваются последующие узлы до тех пор пока не будет достигнут последний конечный узел. Числовая или категориальная метка, соответствующая последнему узлу, является значением зависимой переменной.
.jpg)
Рис. 1. Графическое окно бинарного дерева решений.
Меню "Click to display" (рис. 1) служит для выбора информации о выделенном узле дерева решений. Предусмотрены следующие возможные пункты меню:
|
Пункт меню "Click to display" |
Назначение |
|
Identity |
Отображается номер узла, вид узла: конечный или промежуточный, и правило выбора узла (рис. 2) |
|
Variable ranges |
Приводится размах каждой независимой переменной для указанного узла (рис. 3) |
|
Node statistics |
Статистические данные по выделенному узлу: количество независимых переменных, соответствующие выделенному узлу по исходной выборке; среднее арифметическое и стандартное отклонение зависимой переменной (рис. 4). |
.jpg)
Рис. 2.
.jpg)
Рис. 2.
.jpg)
Рис. 3.
Для отображения интересующей информации об узлах необходимо сначала выбрать соответствующую команду в меню "Click to display" и затем выделить мышью один из узлов дерева решений.
Меню "Pruning level" отображает число уровней полного дерева решений и количество уровней, которые были удалены из него. Например, значения "1 of 4" соответствуют полному дереву решений, состоящему из 4 уровней (рис. 1) и одному уровню, который был удален при формировании сокращенного дерева решений (рис. 5). Изменение числа удаляемых уровней выполняется при помощи кнопок ![]() .
.
.jpg)
Рис. 5. Пример сокращенного дерева решений. Удален один уровень.
Меню "Magnification" служит для изменения масштаба отображения дерева решений в графическом окне.
treedisp(T,'param1',val1,'param2',val2,...) дополнительные параметры 'param1', 'param2',: задаются в виде пары "название параметра, значение" и позволяют определить:
|
Название параметра 'param' |
Назначение и возможные значения val |
|
'names' |
Определяет метки независимых переменных в графическом окне. Значения 'names' задаются в виде массива ячеек. Порядок элементов в массиве ячеек должен соответствовать последовательности независимых переменных (столбцов) матрицы Х, передаваемой как входной аргумент функции treefit. |
|
'prunelevel' |
Начальный уровень при формировании сокращенного дерева решений. Задается как целое число. |
Примеры использования функции treedisp
Графическое отображение иерархической нелинейной регрессионной модели вида ![]() . Зависимая переменная задана на числовой шкале.
. Зависимая переменная задана на числовой шкале.
>> x=1:1:100;
>> x=[x' x' x'];
>> x1=normrnd(0,10,100,3);
>> X=x+x1;
>> y=1:2:200;
>> y1=normrnd(0,2,1,100);
>> y=y+y1;
>> T = treefit(X,y');
>> treedisp(T);
.jpg)
Графическое отображение иерархической нелинейной регрессионной модели вида ![]() . Зависимая переменная задана на числовой шкале. Метки независимых переменных в графическом окне определены с помощью массива ячеек names. При отображении дерева решений задан начальный уровень prunelevel.
. Зависимая переменная задана на числовой шкале. Метки независимых переменных в графическом окне определены с помощью массива ячеек names. При отображении дерева решений задан начальный уровень prunelevel.
>> x=1:1:100;
>> x=[x' x' x'];
>> x1=normrnd(0,10,100,3);
>> X=x+x1;
>> y=1:2:200;
>> y1=normrnd(0,2,1,100);
>> y=y+y1;
>> T = treefit(X,y');
>> names={'first', 'second', 'third'};
>> prunelevel=1;
>> treedisp(T, 'names', names, 'prunelevel', prunelevel);
.jpg)
Графическое отображение бинарного дерева при решении задачи классификации. Зависимая переменная задана на категориальной шкале при помощи вектора строк.
>> load fisheriris
>> t = treefit(meas,species);
>> treedisp(t);
.jpg)
treefit - Построение графа возможных решений на основе исходных данных
Синтаксис
T = treefit(X,y)
T = treefit(X,y,'param1',val1,'param2',val2,...)
Описание
T = treefit(X,y) функция предназначена для расчета структуры Т, определяющей параметры иерархической нелинейной регрессионной модели или бинарного дерева классификации наблюдений для матрицы независимых переменных Х и вектора значений зависимой переменной y. Размерность матрицы Х - n×m, где n - число наблюдений, m - количество независимых переменных. Строки Х соответствуют наблюдениям, столбцы Х - независимым переменным. Число элементов вектора y должно быть равно n. Вектор y может быть задан как вектор числовых значений, вектор строк или массив ячеек со строковыми элементами. В 1-м случае решается задача регрессии, во 2-м и 3-м случаях - задача классификации. Выходная переменная T определяет бинарное дерево решений, в котором промежуточные узлы делятся ветвями на 2 возможных решения. В качестве условия выбора направления перехода выступает ограничение на значение независимой переменной.
T = treefit(X,y,'param1',val1,'param2',val2,...) дополнительные параметры 'param1', 'param2',… задаются в виде пары "название параметра, значение" и позволяют задать:
1. для задач регрессии и классификации
|
Название параметра - 'param' |
Назначение и возможные значения val |
|
'catidx' |
Вектор номеров столбцов матрицы независимых переменных Х заданных на категориальной шкале |
|
'method' |
Вид решаемой задачи: 'method'='classification', решается задача классификации, 'method'='regression', решается задача регрессии. Если наблюдения зависимой переменной y заданы как строковые значения, то 'method' по умолчанию принимается равным 'classification'. Для y(i) заданных на числовой шкале 'method' по умолчанию принимается равным 'regression'. |
|
'splitmin' |
Минимальное число наблюдений в исходной выборке X, y соответствующее узлу бинарного дерева решений, при котором возможно его последующее деление. Значение по умолчанию - 10. |
|
'prune' |
Параметр позволяет задать возможность расчета сокращенных иерархических регрессионных моделей. Для 'prune'='on' рассчитываются параметры полного и последовательности сокращенных иерархических регрессионных моделей. Если 'prune'='off', то определяются параметры полной иерархической регрессионной модели. Значение по умолчанию 'prune'='on'. |
2. для задачи классификации
|
Название параметра - 'param' |
Назначение и возможные значения val |
|
'cost' |
Параметр позволяет задать погрешность классификации точки -го класса в i-й класс. Значение 'cost' задается в виде матрицы С с размерностью р×р, где р - количество значений (классов) зависимой переменной. По умолчанию C(i,j)=1 если i≠j, и C(i,j)=0 если i=j. Значение 'cost' может быть также задано в виде структуры S с двумя полями: S.group -названия групп; S.cost -матрица погрешностей классификации. |
|
'splitcriterion' |
Критерий формирования бинарного дерева решений. Возможные значения 'splitcriterion': 'gdi' - формирование узлов дерева решений выполняется на основе индексов различия Джини; 'twoing' - используется правило максимального соответствия пар значений; 'deviance' - деление выполняется по правилу минимизации максимальной дисперсии. Значение по умолчанию 'splitcriterion'='gdi'. |
|
'priorprob' |
Параметр задает априорные вероятности для каждого класса по зависимой переменной y. Значения параметра 'priorprob' определяются вектором. Каждый элемент вектора значений 'priorprob' соответствует априорной вероятности для отдельного класса по y. Значение 'priorprob' может быть задано как структура S с двумя полями: S.group - названия классов по y; S.prob -вектор соответствующих вероятностей. |
Примеры использования функции treefit
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале.
. Зависимая переменная y определена на числовой шкале.
>> x=1:1:100;
>> x=[x' x' x'];
>> x1=normrnd(0,10,100,3);
>> X=x+x1;
>> y=1:2:200;
>> y1=normrnd(0,2,1,100);
>> y=y+y1;
>> T = treefit(X,y');
>> treedisp(T);
.jpg)
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Задано минимальное число наблюдений для дальнейшего деления промежуточного узла 'splitmin'=20 и отменена возможность расчета параметров последовательности сокращенных иерархических регрессионных моделей 'prune'='off'.
. Зависимая переменная y определена на числовой шкале. Задано минимальное число наблюдений для дальнейшего деления промежуточного узла 'splitmin'=20 и отменена возможность расчета параметров последовательности сокращенных иерархических регрессионных моделей 'prune'='off'.
>> x=1:1:100;
>> x=[x' x' x'];
>> x1=normrnd(0,10,100,3);
>> X=x+x1;
>> y=1:2:200;
>> y1=normrnd(0,2,1,100);
>> y=y+y1;
>> T = treefit(X,y', 'prune','off', 'splitmin',20);
>> treedisp(T);
.jpg)
В приведенном ниже примере регрессии используется категориальная независимая переменная Model_Year (в функции treefit 'catidx'=2).
>> load carsmall
>> x = [Weight,Model_Year];
>> Weight
Weight =
3504
3693
3436
……………………..
>> Model_Year
Model_Year =
70
70
70
……………………..
76
76
……………………..
82
82
82
>> MPG
MPG =
18.0000
15.0000
18.0000
……………………..
>> y = MPG;
>> t = treefit(x,y,'catidx',2);
>> treedisp(t,'name',{'Wt' 'Yr'});
.jpg)
Задача классификации для 4 независимых переменных meas, заданных на числовой шкале, и зависимой переменной species, элементы вектора которой заданы как 3 значения по категориальной шкале.
>> load fisheriris
>> meas
meas =
5.1000 3.5000 1.4000 0.2000
4.9000 3.0000 1.4000 0.2000
4.7000 3.2000 1.3000 0.2000
4.6000 3.1000 1.5000 0.2000
5.0000 3.6000 1.4000 0.2000
5.4000 3.9000 1.7000 0.4000
4.6000 3.4000 1.4000 0.3000
……………………………………..
>> species
species =
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
…………
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
……………
'virginica'
'virginica'
'virginica'
'virginica'
'virginica'
>> t = treefit(meas,species);
>> treedisp(t);
.jpg)
Решается задача классификации для 4 независимых переменных meas и зависимой переменной species. В качестве критерия формирования бинарного дерева решений используется правило минимизации максимальной дисперсии.
>> load fisheriris
>> t = treefit(meas,species, 'splitcriterion', 'deviance');
>> treedisp(t);
.jpg)
Решается задача классификации для 4 независимых переменных meas и зависимой переменной species. В качестве дополнительных параметров заданы: матрица погрешностей cost и вектор априорных вероятностей priorprob.
>> load fisheriris
>> cost=[0 0.8 0.9; 0.8 0 0.9; 0.8 0.9 0];
>> priorprob=[0.3 0.5 0.2];
>> t = treefit(meas,species,'cost',cost,'priorprob',priorprob);
>> treedisp(t);
.jpg)
Решается задача классификации для 4 независимых переменных meas и зависимой переменной species. Дополнительные параметры погрешности классификации и априорные вероятностей классов зависимой переменной заданы как структуры S1, S2 соответственно.
>> load fisheriris
>> S1.group=['setosa '; 'versicolor'; 'virginica '];
>> S1.cost=[0 0.9 0.9; 0.8 0 0.6; 0.7 0.8 0];
>> S2.group=['setosa '; 'versicolor'; 'virginica '];
>> S2.prob=[0.3 0.5 0.2];
>> t = treefit(meas,species,'cost', S1,'priorprob',S2);
>> treedisp(t);
.jpg)
treeprune - Исключение незначимых решений в графе возможных решений
Синтаксис
T2 = treeprune(T1,'level',level)
T2 = treeprune(T1,'nodes',nodes)
T2 = treeprune(T1)
Описание
T2 = treeprune(T1,'level',level) функция предназначена для получения сокращенной до уровня 'level' иерархической регрессионной модели T2 из начального бинарного дерева решений T1. T1 является выходной переменной функции treefit. Значение параметра 'level' - level должно быть целым положительным числом. Если level=0 то T2 будет получено без сокращения T1. Исходное бинарное дерево решений T1 сокращается по оптимальной схеме, т.е. в первую очередь удаляются промежуточные узлы соответствующие наименьшему уменьшению погрешности иерархической регрессионной модели.
T2 = treeprune(T1,'nodes',nodes) функция позволяет сформировать сокращенное бинарное дерево решений T2 из начальной иерархической регрессионной модели T1. Конечные узлы Т2 определяются промежуточные узлы номера которых перечислены в векторе nodes. Если nodes(i) является подчиненным nodes(j), то nodes(i) будет удален, а nodes(j) станет конечным узлом Т2. Элементами вектора nodes должны быть целые положительные числа. Номера узлов можно определить на графике бинарного дерева решений, полученного с помощью функции treedisp.
T2 = treeprune(T1) функция возвращает структуру Т2 задающую тоже бинарное дерево решений, что и входной параметр T1. В отличии от Т1 в Т2 будет внесена информация по оптимальному сокращению бинарного дерева решений. Такой вариант синтаксиса функции treeprune используется в 2 случаях: 1. если Т1 была получена посредством сокращения другого дерева решений; 2. если Т1 была рассчитана с использованием treefit с параметром 'prune'='off'.
Процедура сокращения исходного дерева решений позволяет перевести промежуточные узлы в конечные с удалением последних из начальной иерархической регрессионной модели.
Примеры использования функции treeprune
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Исходное бинарное дерево решений сокращается на 5 уровней. Приведены графики начального и сокращенного бинарных деревьев решений.
. Зависимая переменная y определена на числовой шкале. Исходное бинарное дерево решений сокращается на 5 уровней. Приведены графики начального и сокращенного бинарных деревьев решений.
>> x=1:1:100;
>> x=[x' x' x'];
>> x1=normrnd(0,10,100,3);
>> X=x+x1;
>> y=1:2:200;
>> y1=normrnd(0,2,1,100);
>> y=y+y1;
>> T1 = treefit(X,y');
>> level=5;
>> T2 = treeprune(T1,'level',level);
>> treedisp(T1);
.jpg)
>> treedisp(T2);
.jpg)
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Сокращение выполняется для промежуточных узлов заданных вектором номеров nodes.
. Зависимая переменная y определена на числовой шкале. Сокращение выполняется для промежуточных узлов заданных вектором номеров nodes.
>> x=1:1:20;
>> x=[x' x'];
>> x1=normrnd(0,10,20,2);
>> X=x+x1;
>> y=1: 2:40;
>> y1=normrnd(0,2,1,20);
>> y=y+y1;
>> T1 = treefit(X,y');
>> treedisp(T1);
.jpg)
>> nodes = [2 4];
>> T2 = treeprune(T1,'nodes',nodes);
>> treedisp(T2);
.jpg)
Задача классификации для 4 независимых переменных meas, заданных на числовой шкале, и зависимой переменной species, элементы вектора которой заданы по 3-м классам на категориальной шкале. Исходное бинарное дерево решений сокращается на 2 уровня. Приведены графики начального и сокращенного бинарных деревьев решений.
>> load fisheriris
>> T1 = treefit(meas,species);
>> treedisp(T1);
.jpg)
>> level=2;
>> T2 = treeprune(T1,'level',level);
>> treedisp(T2);
.jpg)
Задача классификации для 4 независимых переменных meas, заданных на числовой шкале, и зависимой переменной species, элементы вектора которой заданы по 3-м классам на категориальной шкале. Сокращение выполняется для промежуточных узлов заданных вектором номеров nodes.
>> load fisheriris
>> T1 = treefit(meas,species);
>> treedisp(T1);
.jpg)
>> nodes = [4 6];
>> T2 = treeprune(T1,'nodes',nodes);
>> treedisp(T2);
.jpg)
treetest - Оценка погрешности узлов графа возможных решений
Синтаксис
cost = treetest(T,'resubstitution')
cost = treetest(T,'test',X,y)
cost = treetest(T,'crossvalidate',X,y)
[cost,secost,ntnodes,bestsize] = treetest(...)
[...] = treetest(...,'param1',val1,'param2',val2,...)
Описание
cost = treetest(T,'resubstitution') функция позволяет рассчитать погрешность иерархической нелинейной регрессионной модели определяемой бинарным деревом решений Т методом обратной подстановки исходных значений зависимой и независимых переменных. Входной аргумент Т формируется с помощью функции treefit. Погрешность иерархической нелинейной регрессионной модели определяется как сумма вероятностей неверного определения i-х значений зависимой переменной p(i) по всем конечным узлам. Если при формировании Т решалась задача классификации, то вероятностью p(i) является отношение числа неверных классификаций по i-му значению зависимой переменной из начального множества данных к объему исходной выборки. Если при расчете Т была решена задача регрессии, то в качестве p(i) принимается средняя квадратическая ошибка при определении i-го значения зависимой переменной по исходной выборке. Выходная переменная cost является вектором погрешностей для последовательности иерархических регрессионных моделей, полученных в процессе совращения уровней в исходном бинарном дереве решений Т. Поскольку расчет вектора ошибок основан на исходной выборке по которой была рассчитана структура Т, то элементы вектора cost будут представлять нижнюю границу доверительного интервала погрешности при использовании новой выборки.
cost = treetest(T,'test',X,y) функция предназначена для расчета вектора погрешностей cost иерархической нелинейной регрессионной модели определяемой структурой Т по тестовой 'test' выборке X, y. Х матица значений независимых переменных. Столбцы Х соответствуют независимым переменным, строки - наблюдениям. y - вектор значений зависимой переменой. Тестовая выборка и исходная выборка, использованная в treefit при расчете Т, должны быть различны. Количество и порядок независимых переменных, столбцов матриц Х в исходной и тестовой выборках, должно быть одинаковым.
cost = treetest(T,'crossvalidate',X,y) функция предназначена для расчета вектора погрешностей cost иерархической нелинейной регрессионной модели, заданной структурой Т, методом перекрестной подстановки 'crossvalidate'. Матрица независимых переменных Х и вектор значений зависимой переменной y являются исходной выборкой, по которой была рассчитана структура Т.
Алгоритм расчета погрешности регрессионной модели методом перекрестной подстановки включает следующие этапы:
1. Исходная выборка X, y делится на 10 подгрупп с приблизительно равным объемом, элементы которых выбираются случайным образом. Если при формировании Т решалась задача классификации, то подгруппы формируются с приблизительно одинаковыми вероятностями извлечь значение y(i) из каждой подгруппы.
2. Выбирается одна из полученных подгрупп. Определяются значения из X, y не попавшие в подгруппу. Эти значения используются для расчета бинарного дерева решений иерархической нелинейной регрессионной модели.
3. По полученному бинарному дереву решений на основе элементов подгруппы рассчитывается погрешность модели.
4. Расчет по п. 2-3 повторяется по оставшимся подгруппам. На основе полученных погрешностей для отдельных подгрупп рассчитывается общая погрешность регрессионной модели по исходной выборке.
[cost,secost,ntnodes,bestsize] = treetest(...) функция позволяет рассчитать: 1. cost - вектор погрешностей иерархической нелинейной регрессионной модели; 2. secost - вектор стандартных ошибок для элементов вектора cost; 3. ntnodes - вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений; 4. bestsize - скаляр, определяющий оптимальный уровень сокращения полного дерева решений Т. Если bestsize=0, то оптимальным будет полное бинарное дерево решений Т. Величина bestsize должна соответствовать наименьшему бинарному дереву решений, обеспечивающему погрешность иерархической нелинейной регрессионной модели равной минимальной погрешности плюс ее стандартная ошибка.
[...] = treetest(...,'param1',val1,'param2',val2,...) дополнительные входные параметры 'param1', 'param2' задаются в виде пары "название параметра, значение" и позволяют определить:
|
Название параметра 'param' |
Назначение и возможные значения val |
|
'nsamples' |
Количество подгрупп при использовании метода перекрестной подстановки для расчета вектора погрешностей последовательности регрессионных моделей. Значение по умолчанию - 10. |
|
'treesize' |
Критерий расчета величины bestsize. Возможны значения: 'se' - величина bestsize должна соответствовать наименьшему бинарному дереву решений, обеспечивающему погрешность иерархической нелинейной регрессионной модели равной минимальной погрешности плюс ее стандартная ошибка; 'min' - bestsize выбирается так, чтобы обеспечивалась минимальное значение погрешности регрессионной модели. |
Примеры использования функции treetest
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается методом обратной подстановки.
. Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается методом обратной подстановки.
>> x=1:1:20;
>> x=[x' x'];
>> x1=normrnd(0,10,20,2);
>> X=x+x1;
>> y=1:2:40;
>> y1=normrnd(0,2,1,20);
>> y=y+y1;
>> T = treefit(X,y');
>> treedisp(T);
.jpg)
>> cost = treetest(T,'resubstitution')
cost =
58.4830
77.3941
99.2253
142.7998
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается для тестовой выборки Xtest, Ytest.
. Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается для тестовой выборки Xtest, Ytest.
>> x=1:1:20;
>> x=[x' x'];
>> x1=normrnd(0,1,20,2);
>> X=x+x1;
>> y=1:2:40;
>> y1=normrnd(0,2,1,20);
>> y=y+y1;
>> T = treefit(X,y');
>> treedisp(T);
.jpg)
>> Xtest=2:1:21;
>> Xtest =[ Xtest' Xtest'];
>> Xtest1=normrnd(0,1,20,2);
>> Xtest = Xtest + Xtest1;
>> Ytest =1:2:22;
>> Ytest1=normrnd(0,3,1,20);
>> Ytest = Ytest + Ytest1;
>> cost = treetest(T,'test', Xtest, Ytest')
cost =
168.0132
146.3590
134.4918
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается методом перекрестной подстановки. Функция возвращает вектор погрешностей иерархической нелинейной регрессионной модели, вектор стандартных ошибок для элементов вектора погрешностей, вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений, оптимальный уровень сокращения полного дерева решений.
. Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается методом перекрестной подстановки. Функция возвращает вектор погрешностей иерархической нелинейной регрессионной модели, вектор стандартных ошибок для элементов вектора погрешностей, вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений, оптимальный уровень сокращения полного дерева решений.
>> x=1:1:20;
>> x=[x' x'];
>> x1=normrnd(0,1,20,2);
>> X=x+x1;
>> y=1:2:40;
>> y1=normrnd(0,2,1,20);
>> y=y+y1;
>> T = treefit(X,y');
>> treedisp(T);
.jpg)
>> [cost,secost,ntnodes,bestsize]= treetest(T,'crossvalidate',X,y')
cost =
41.2422
49.6159
144.4373
secost =
10.3460
13.7285
29.2722
ntnodes =
3
2
1
bestsize =
1
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается методом перекрестной подстановки. Функция возвращает вектор погрешностей иерархической нелинейной регрессионной модели, вектор стандартных ошибок для элементов вектора погрешностей, вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений, оптимальный уровень сокращения полного дерева решений. В качестве дополнительных параметров заданы: количество подгрупп при использовании метода перекрестной подстановки - 9, критерий расчета величины bestsize - 'min'.
. Зависимая переменная y определена на числовой шкале. Погрешность регрессионной модели рассчитывается методом перекрестной подстановки. Функция возвращает вектор погрешностей иерархической нелинейной регрессионной модели, вектор стандартных ошибок для элементов вектора погрешностей, вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений, оптимальный уровень сокращения полного дерева решений. В качестве дополнительных параметров заданы: количество подгрупп при использовании метода перекрестной подстановки - 9, критерий расчета величины bestsize - 'min'.
>> x=1:1:20;
>> x=[x' x'];
>> x1=normrnd(0,1,20,2);
>> X=x+x1;
>> y=1:2:40;
>> y1=normrnd(0,2,1,20);
>> y=y+y1;
>> T = treefit(X,y');
>> treedisp(T);
.jpg)
>> [cost,secost,ntnodes,bestsize]= treetest(T,'crossvalidate',X,y','nsamples',9,'treesize','min')
cost =
31.9920
39.8811
148.5497
secost =
7.1432
8.0561
29.1186
ntnodes =
3
2
1
bestsize =
0
Рассматривается задача классификации. Зависимая переменная задана на категориальной шкале при помощи вектора строк. Погрешность классификации рассчитывается методом обратной подстановки.
>> load fisheriris
>> t = treefit(meas,species);
>> treedisp(t);
.jpg)
>> cost = treetest(t,'resubstitution')
cost =
0.0200
0.0267
0.0400
0.3333
0.6667
Рассматривается задача классификации. Зависимая переменная задана на категориальной шкале при помощи вектора строк. Погрешность классификации рассчитывается методом перекрестной подстановки. Функция возвращает вектор погрешностей иерархической нелинейной регрессионной модели, вектор стандартных ошибок для элементов вектора погрешностей, вектор чисел конечных узлов последовательности сокращенных бинарных деревьев решений, оптимальный уровень сокращения полного дерева решений. В качестве дополнительных параметров заданы: количество подгрупп при использовании метода перекрестной подстановки - 15, критерий расчета величины bestsize - 'min'.
>> load fisheriris
>> t = treefit(meas,species);
>> treedisp(t);
.jpg)
>> [cost,secost,ntnodes,bestsize]= treetest(t,'crossvalidate',meas, species,'nsamples',15,'treesize','min')
cost =
0.0533
0.0667
0.0667
0.3667
0.7000
secost =
0.0179
0.0200
0.0200
0.0316
0.0316
ntnodes =
5
4
3
2
1
bestsize =
0
Выполняется оптимизация бинарного дерева решения для классификации наблюдений методом перекрестной подстановки. Сплошная линия на графике показывает изменение погрешности классификации в зависимости от числа сокращаемых уровней. Штрихпунктирная линия на графике показывает положение минимального значения погрешности при классификации плюс стандартная ошибка классификации. Маркер отмечен оптимальный уровень при сокращении полного бинарного дерева решений.
1. Расчет параметров полной иерархической регрессионной модели.
>> load fisheriris;
>> t = treefit(meas,species','splitmin',5);
2. Поиск бинарного дерева решений соответствующего минимальной погрешности.
>> [c,s,n,best] = treetest(t,'cross',meas,species);
>> tmin = treeprune(t,'level',best);
3. Графическое представление изменения погрешности классификации в зависимости от числа сокращаемых уровней, положения минимального значения погрешности при классификации плюс стандартной ошибки классификации и оптимального уровеня при сокращении полного бинарного дерева решений.
>> [mincost,minloc] = min(c);
>> plot(n,c,'b-o', n,c+s,'r:', n(best+1),c(best+1),'bs',n,(mincost+s(minloc))*ones(size(n)),'k--');
>> xlabel('Tree size (number of terminal nodes)')
>> ylabel('Cost')
.jpg)
treeval - Оценка параметров регрессионной модели с использованием графа возможных решений
Синтаксис
YFIT = treeval(T,X)
YFIT = treeval(T,X,subtrees)
[YFIT,NODE] = treeval(...)
[YFIT,NODE,CNAME] = treeval(...)
Описание
YFIT = treeval(T,X) функция позволяет определить значения зависимой переменной YFIT по иерархической нелинейной регрессионной модели, параметры которой задаются структурой T, для значений независимых переменных Х. Структура Т формируется как выходной аргумент функции treefit. Х задается как матрица с размерностью n×m, где n - число наблюдений, m - количество независимых переменных. Строки Х соответствуют наблюдениям, столбцы Х - независимым переменным. Выходная переменная YFIT является вектором значений с числом элементов равным n. Значение YFIT(j) рассчитывается согласно строкам X(j,:). Если при формировании структуры Т решалась задача классификации, то YFIT(j) является номером класса, к которому принадлежит точка с координатами X(j,:) в пространстве независимых переменных. Для определения названия класса соответствующего номеру YFIT(j) используется третий выходной аргумент cname (см. ниже).
YFIT = treeval(T,X,subtrees) дополнительный входной параметр subtrees задает число удаляемых уровней при формировании последовательности сокращенных иерархических регрессионных моделей и расчете по этим моделям значений зависимой переменной YFIT для матрицы независимых переменных Х. subtrees задается как вектор целых чисел: нулевое значение соответствует полному дереву решений, 1 - дереву решений сокращенному на один уровень и т.д. Структура Т должна быть сформирована с наличием в ней информации о последовательности сокращенных бинарных деревьев функциями treefit или prunetree. Если вектор subtrees содержит k элементов, а матрица Х n строк, тогда YFIT будет матрицей с размерностью n×k, где j-й столбец значений зависимых переменных будет рассчитан по дереву решений сокращенному на subtrees(j) уровня. Элементы в векторе subtrees должны быть расположены по возрастанию.
[YFIT,NODE] = treeval(...) кроме значений зависимой переменной функция возвращает массив номеров узлов NODE соотнесенных c каждой строкой матрицы независимых переменных Х(j,:). Размерность YFIT и NODE будет совпадать. С помощью функции treedisp в интерактивном режиме можно определить номер каждого выделенного в графическом окне узла в бинарном дереве решений.
[YFIT,NODE,CNAME] = treeval(...) функция возвращает массив ячеек CNAME, содержащий названия классов найденных по дереву решений Т. Выходная переменная CNAME используется только тогда, когда структура Т была получена при решении задачи классификации.
Примеры использования функции treeval
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Значения зависимой переменной рассчитываются в точках xnew=2.5:10:100.
. Зависимая переменная y определена на числовой шкале. Значения зависимой переменной рассчитываются в точках xnew=2.5:10:100.
>> x=1:1:100;
>> x=[x' x' x'];
>> x1=normrnd(0,10,100,3);
>> X=x+x1;
>> y=1:2:200;
>> y1=normrnd(0,2,1,100);
>> y=y+y1;
>> T = treefit(X,y');
>> xnew=2.5:10:100;
>> xnew=[xnew' xnew' xnew'];
>> YFIT = treeval(T, xnew)
YFIT =
6.1347
22.6420
37.8906
65.8118
77.8094
106.1516
121.3727
135.8064
178.4442
190.7365
Рассматривается задача регрессии вида ![]() . Зависимая переменная y определена на числовой шкале. Значения зависимой переменной рассчитываются в точках xnew1=2.5:2:20, xnew2=1.5:2:20. Зависимые переменные рассчитываются для полного дерева решений и иерархических моделей, сокращенных на 1 и 2 уровня: subtrees =[0 1 2]. Функция возвращает матрицы значений зависимой переменной YFIT и соответствующих им узлов бинарного дерева решений NODE.
. Зависимая переменная y определена на числовой шкале. Значения зависимой переменной рассчитываются в точках xnew1=2.5:2:20, xnew2=1.5:2:20. Зависимые переменные рассчитываются для полного дерева решений и иерархических моделей, сокращенных на 1 и 2 уровня: subtrees =[0 1 2]. Функция возвращает матрицы значений зависимой переменной YFIT и соответствующих им узлов бинарного дерева решений NODE.
>> x=1: 1:20;
>> x=[x' x'];
>> x1=normrnd(0,10,20,2);
>> X=x+x1;
>> y=1: 2:40;
>> y1=normrnd(0,2,1,20);
>> y=y+y1;
>> T = treefit(X,y');
>> xnew1=2.5: 2:22;
>> xnew2=1.5: 2:20;
>> xnew=[xnew1' xnew2'];
>> subtrees =[0 1 2];
>> [YFIT,NODE] = treeval(T,X,subtrees)
YFIT =
3.2534 3.2534 14.0020
14.6854 15.6556 14.0020
8.8213 15.6556 14.0020
8.8213 15.6556 14.0020
3.2534 3.2534 14.0020
14.6854 15.6556 14.0020
14.6854 15.6556 14.0020
14.6854 15.6556 14.0020
8.8213 15.6556 14.0020
14.6854 15.6556 14.0020
24.7537 15.6556 14.0020
24.7537 15.6556 14.0020
14.6854 15.6556 14.0020
14.6854 15.6556 14.0020
35.0736 35.0736 35.0736
24.7537 15.6556 14.0020
33.4583 33.4583 33.4583
35.0736 35.0736 35.0736
35.0736 35.0736 35.0736
35.0736 35.0736 35.0736
NODE =
6 6 4
11 7 4
8 7 4
8 7 4
6 6 4
11 7 4
11 7 4
11 7 4
8 7 4
11 7 4
10 7 4
10 7 4
11 7 4
11 7 4
3 3 3
10 7 4
5 5 5
3 3 3
3 3 3
3 3 3
Задача классификации для 4 независимых переменных meas, заданных на числовой шкале, и зависимой переменной species, элементы вектора которой заданы по 3-м классам на категориальной шкале. Определение классов по зависимой переменной определяется для матрицы new_meas.
>> load fisheriris
>> meas
meas =
5.1000 3.5000 1.4000 0.2000
4.9000 3.0000 1.4000 0.2000
4.7000 3.2000 1.3000 0.2000
4.6000 3.1000 1.5000 0.2000
5.0000 3.6000 1.4000 0.2000
5.4000 3.9000 1.7000 0.4000
4.6000 3.4000 1.4000 0.3000
……………………………………..
>> species
species =
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
'setosa'
…………
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
'versicolor'
……………
'virginica'
'virginica'
'virginica'
'virginica'
'virginica'
>> t = treefit(meas,species);
>> new_meas=[5 3.1 1.35 0.32; 4 5.1 2.35 1.32; 2 0.1 3.35 0.22;]
new_meas =
5.0000 3.1000 1.3500 0.3200
4.0000 5.1000 2.3500 1.3200
2.0000 0.1000 3.3500 0.2200
>> YFIT = treeval(t, new_meas)
YFIT =
1
1
2
Задача классификации для 4 независимых переменных meas, заданных на числовой шкале, и зависимой переменной species, элементы вектора которой заданы по 3-м классам на категориальной шкале. Определение классов по зависимой переменной определяется для матрицы new_meas. Зависимые переменные рассчитываются для полного дерева решений и иерархической модели, сокращенной на 1 уровень: subtrees =[0 1]. Функция возвращает матрицы значений зависимой переменной YFIT, соответствующих им узлов бинарного дерева решений NODE и названия классов CNAME.
>> load fisheriris
>> t = treefit(meas,species);
>> new_meas=[5 3.1 1.35 0.32; 4 5.1 2.35 1.32; 2 0.1 3.35 0.22;];
>> subtrees =[0 1 2];
>> [YFIT,NODE,CNAME] = treeval(t, new_meas, subtrees)
YFIT =
1 1 1
1 1 1
2 2 2
NODE =
2 2 2
2 2 2
8 6 4
CNAME =
'setosa' 'setosa' 'setosa'
'setosa' 'setosa' 'setosa'
'versicolor' 'versicolor' 'versicolor'
ranksum - Ранговый тест Вилкоксона для проверки однородности двух генеральных совокупностей
Синтаксис
p = ranksum(x,y)
[p,h] = ranksum(x,y)
[p,h] = ranksum(x,y,alpha)
[p,h,stats] = ranksum(...)
Описание
p = ranksum(x,y) функция предназначена для проведения двустороннего рангового теста Вилкоксона для проверки нулевой гипотезы состоящей в том, что независимые выборки x и y взяты из генеральных совокупностей с равными медианами. Выборки x и y задаются как векторы. Функция возвращает значение уровня значимости p для проверки нулевой гипотезы. Уровень значимости - вероятность ошибки первого рода, т.е. вероятность неверно отвергнуть нулевую гипотезу, в случае ее справедливости. Если значение p≈0, то нулевая гипотеза может быть отвергнута, т.е. медианы сравниваемых выборок статистически значимо отличаются друг от друга. Выбор критического уровня значимости ![]() для условия принятия нулевой гипотезы
для условия принятия нулевой гипотезы
![]() ,
,
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
Предполагается, что генеральные совокупности, из которых извлекаются выборки, имеют одинаковое непрерывное распределение. Генеральные совокупности могут отличаться только средними значениями. Объем выборок, и как следствие число элементов векторов x, y, могут быть разными.
Ранговый тест Вилкоксона является эквивалентом U теста Манна-Уитни.
[p,h] = ranksum(x,y) функция возвращает значение уровня значимости р при проверке нулевой гипотезы и результат проверки нулевой гипотезы h для критического значения ![]() равного 0,05. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза принимается если h=0 при ![]() . Если h=1, то нулевая гипотеза может быть отвергнута при
. Если h=1, то нулевая гипотеза может быть отвергнута при ![]() , т.е. медианы выборок статистически значимо отличаются друг от друга.
, т.е. медианы выборок статистически значимо отличаются друг от друга.
[p,h] = ranksum(x,y,alpha) входной параметр alpha позволяет задать значение критического уровня значимости при проверке нулевой гипотезы. По умолчанию alpha=0,05.
[p,h,stats] = ranksum(...) функция возвращает структуру stats содержащую одно или два поля:
1. stats.ranksum - значение ранговой статистики;
2. stats.zval - значение Z статистики. Эта статистика рассчитывается при большом объеме выборки и значение уровня значимости р будет рассчитано исходя из нормальной аппроксимации распределения статистики Z.
Примеры использования функции рангового теста Вилкоксона на равенство медиан двух независимых выборок
Проверка равенства медиан двух независимых выборок распределенных по непрерывному закону равной вероятности с одинаковой величиной размаха и величинами математических ожиданий равных 0 и 0,75 для выборок x и y соответственно. Объем выборок равен 10 и 15 элементам. Функция возвращает значение уровня значимости p.
>> x = unifrnd(0,1,10,1);
>> y = unifrnd(.25,1.25,15,1);
>> p = ranksum(x,y)
p =
0.1272
Проверка гипотезы о равенстве медиан двух независимых выборок распределенных по нормальному закону с одинаковыми величинами средних квадратических отклонений и величинами математических ожиданий равными 0 и 1 для выборок x и y соответственно. Объем выборок равен 20 и 30 элементам. Функция возвращает значение уровня значимости p и результат проверки нулевой гипотезы для критического уровня значимости равного 0,01.
>> x = normrnd(0,1,20,1);
>> y = normrnd(1,1,30,1);
>> [p h] = ranksum(x,y,0.01)
p =
0.0065
h =
1
Проверка гипотезы о равенстве медиан двух независимых выборок распределенных по нормальному закону с одинаковыми величинами средних квадратических отклонений и величинами математических ожиданий равными 0 и 0,1 для выборок x и y соответственно. Объем выборок равен 10 элементам. Функция возвращает значение уровня значимости p и результат проверки нулевой гипотезы для критического уровня значимости равного 0,02. Кроме значений p и h функция возвращает структуру stats. Графически тест можно представить при помощи функции boxplot.
>> x = normrnd(0,1,10,1);
>> y = normrnd(0.1,1,10,1);
>> [p h stats] = ranksum(x,y,0.01)
p =
0.9097
h =
0
stats =
zval: -0.1134
ranksum: 103
>> boxplot([x y],1)
.jpg)
Зависимость величины уровня значимости от разницы между средними арифметическими выборок распределенных по нормальному закону. Объем выборок принят равным 10 элементам.
>> delta = 0:0.1:1;
>> x = normrnd(0,1,10,1);
>> for i=1:length(delta) y = normrnd(delta(i),1,10,1); p(i) = ranksum(x,y); end;
>> plot(delta,p,'o')
>> grid on
.jpg)
Зависимость величины уровня значимости от разницы между математическими ожиданиями и объемом выборок распределенных по нормальному закону. Объем выборок принят равным 10 элементам.
>> delta = 0:0.1:1;
>>n=10;
>> x = normrnd(0,1,n,1);
>> for i=1:length(delta) y = normrnd(delta(i),1,n,1); p1(i) = ranksum(x,y); end;
>>n=20;
>> x = normrnd(0,1,n,1);
>> for i=1:length(delta) y = normrnd(delta(i),1,n,1); p2(i) = ranksum(x,y); end;
>>n=50;
>> x = normrnd(0,1,n,1);
>> for i=1:length(delta) y = normrnd(delta(i),1,n,1); p3(i) = ranksum(x,y); end;
>> plot(delta,p1,'or',delta,p2,'+b',delta,p3,'.g')
>> grid on
.jpg)
signrank
Знаковый ранговый тест Вилкоксона на равенство нулю медианы выборки
Синтаксис
p = signrank(x)
p = signrank(x,m)
p = signrank(x,y)
[p,h] = signrank(...)
[p,h] = signrank(...,alpha)
[p,h,stats] = signrank(...)
Описание
p = signrank(x) функция позволяет провести двусторонний знаковый ранговый тест Вилкоксона для проверки нулевой гипотезы состоящей в том, что медиана выборки x равна нулю. Выборка x задается как вектор. Функция возвращает значение уровня значимости p для проверки нулевой гипотезы. Уровень значимости - вероятность ошибки первого рода, т.е. вероятность неверно отвергнуть нулевую гипотезу, в случае ее справедливости. Если значение p≈0, то нулевая гипотеза может быть отвергнута, т.е. медиана выборки х статистически значимо отличаются от нуля. Выбор критического уровня значимости ![]() для условия принятия нулевой гипотезы
для условия принятия нулевой гипотезы
![]() ,
,
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
Предполагается, что выборка х получена из генеральной совокупности имеющей симметричное относительно медианы непрерывное распределение.
Примечание автора: вариант синтаксиса функции p = signrank(x) в версиях 6.5, 6.51 не работает. Анализ m-функции показывает, что signrank требует в явном виде задать второй входной аргумент. Для того чтобы выполнить тест, соответствующий этому варианту синтаксиса, необходимо явно задать нулевое значение медианы, например p = signrank(x,0).
p = signrank(x,m) функция позволяет провести двусторонний знаковый ранговый тест Вилкоксона на равенство медианы выборки х значению m. Величина m должна быть задана как скаляр.
p = signrank(x,y) функция позволяет провести парный двусторонний тест Вилкоксона для нулевой гипотезы, состоящей в том, что медиана разностного распределения генеральных совокупностей, из которых были сделаны выборки x, y равна нулю. Предполагается, что разностное генеральное распределение, которому соответствует выборка (x-y), является непрерывным и симметричным относительно его медианы. Объем выборок должен быть одинаковым, т.е. length(x)= length(y).
Примечание: гипотеза о равенстве нулю медианы генерального разностного распределения не является эквивалентной гипотезе о равенстве медиан генеральных распределений, из которых были получены x, y. Функция signrank позволяет проверить первую, но не вторую из названных статистических гипотез.
[p,h] = signrank(...) функция возвращает значение уровня значимости р и результат проверки нулевой гипотезы h для значения ![]() равного 0,05. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза принимается если h=0 при ![]() . Если h=1, то нулевая гипотеза может быть отвергнута при
. Если h=1, то нулевая гипотеза может быть отвергнута при ![]() .
.
[p,h] = signrank(...,alpha) входной параметр alpha позволяет задать значение критического уровня значимости при проверке нулевой гипотезы.
[p,h,stats] = signrank(...) функция возвращает структуру stats содержащую одно или два поля:
1. stats.signedrank - значение знаковой ранговой статистики;
2. stats.zval - значение Z статистики. Эта статистика рассчитывается при большом объеме выборки и значение уровня значимости р будет рассчитано исходя из нормальной аппроксимации распределения статистики Z.
Примеры использования функции знакового рангового теста Вилкоксона на равенство нулю медианы выборки
Проверка равенства нулю медиан выборок распределенных по непрерывному закону равной вероятности с величинами математического ожидания равными 0 и 0,1. Объем выборки равен 10 элементам. Функция возвращает значение уровня значимости p.
>> x = unifrnd(-0.9,1.1,10,1);
>> p = signrank (x,0)
p =
1
>> x = unifrnd(-1,1,10,1);
>> p = signrank (x,0)
p =
0.4316
Проверка равенства заданному значению, 0,22, медиан выборок распределенных по нормальному закону с величинами математического ожидания равными 0 и 0,5. Объем выборки равен 35 элементам. Функция возвращает значение уровня значимости p и результат проверки нулевой гипотезы.
>> x = normrnd(0,1,35,1);
>> [p h] = signrank (x,0.22)
p =
0.7064
h =
0
>> x = normrnd(0.5,1,35,1);
>> [p h] = signrank (x,0.22)
p =
0.0248
h =
1
Проверка равенства заданному значению, 0,5, медианы выборки распределенной по нормальному закону с величиной математического ожидания равной 0,1. Объем выборки равен 15 элементам. Функция возвращает значение уровня значимости и результат проверки нулевой гипотезы. При проверке нулевой гипотезы критическое значение уровня значимости принимается равным 0,1. Графическое представление теста выполняется при помощи функции boxplot.
>> x = normrnd(0.1,1,15,1);
>> alpha = 0.1;
>> [p h] = signrank (x,0.5, alpha)
p =
0.1354
h =
0
>> boxplot(x,1)
.jpg)
Проверка равенства заданному значению, 0,7, медиан нескольких выборок распределенных по нормальному закону с величинами математических ожиданий равных 0; 0,5; 1; 1,5. Объем выборок равен 15 элементам. Функция возвращает значение уровня значимости, результат проверки нулевой гипотезы и структуру stats. При проверке нулевой гипотезы критическое значение уровня значимости принимается равным 0,07. Графическое представление теста выполняется при помощи функции boxplot.
>> x1 = normrnd(0,1,15,1);
>> x2 = normrnd(0.5,1,15,1);
>> x3 = normrnd(1,1,15,1);
>> x4 = normrnd(1.5,1,15,1);
>> alpha = 0.07;
>> [p1 h1 stats1] = signrank (x1,0.7, alpha)
p1 =
4.2725e-004
h1 =
1
stats1 =
signedrank: 4
>> [p2 h2 stats2] = signrank (x2,0.7, alpha)
p2 =
0.0302
h2 =
1
stats2 =
signedrank: 22
>> [p3 h3 stats3] = signrank (x3,0.7, alpha)
p3 =
0.3028
h3 =
0
stats3 =
signedrank: 41
>> [p4 p4 stats4] = signrank (x4,0.7, alpha)
p4 =
1
p4 =
1
stats4 =
signedrank: 12
>> boxplot([x1 x2 x3 x4],1)
.jpg)
Зависимость величины уровня значимости от разницы между математическими ожиданиями генеральных совокупностей и объемом выборок распределенных по нормальному закону.
>> delta = 0:0.1:1;
>>n=10;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); p1(i) = signrank(x,0); end;
>> n=20;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); p2(i) = signrank (x,0); end;
>>n=50;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); p3(i) = signrank (x,0); end;
>> plot(delta,p1,'or',delta,p2,'+b',delta,p3,'.g')
>> grid on
.jpg)
Проверка равенства нулю медианы выборки из разностной генеральной совокупности (x-y). При проверке нулевой гипотезы критическое значение уровня значимости принимается равным 0,01. Функция возвращает значение уровня значимости p, результат проверки нулевой гипотезы h и структуру stats. Графическое представление теста выполняется при помощи функции boxplot.
>> x = normrnd(0,1,50,1);
>> y = normrnd(0.5,2, 50,1);
>> alpha = 0.01;
>> [p h stats] = signrank (x,y, alpha)
p =
0.7832
h =
0
stats =
zval: -0.2751
signedrank: 609
>> boxplot([x-y,x,y],1)
.jpg)
signtest - Знаковый тест для проверки гипотезы о равенстве медиан двух выборок
Синтаксис
p = signtest(x)
p = signtest(x,m)
p = signtest(x,y)
[p,h] = signtest(...)
[p,h] = signtest(...,alpha)
[p,h,stats] = signtest(...)
Описание
p = signtest(x) функция предназначена для проведения двустороннего знакового теста для проверки нулевой гипотезы состоящей в том, что медиана выборки x равна нулю. Выборка x задается как вектор. Функция возвращает значение уровня значимости p для проверки нулевой гипотезы. Уровень значимости - вероятность ошибки первого рода, т.е. вероятность неверно отвергнуть нулевую гипотезу, в случае ее справедливости. Если значение p≈0, то нулевая гипотеза может быть отвергнута, т.е. медиана выборки х статистически значимо отличаются от нуля. Выбор критического уровня значимости ![]() для условия принятия нулевой гипотезы
для условия принятия нулевой гипотезы
![]() ,
,
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
Предполагается, что выборка х получена из генеральной совокупности имеющей симметричное относительно медианы непрерывное распределение.
Примечание автора: вариант синтаксиса функции p=signtest(x) в версиях 6.5, 6.51 не работает. Анализ m-функции показывает, что signtest требует в явном виде задать второй входной аргумент. Для того чтобы выполнить тест, соответствующий этому варианту синтаксиса, необходимо явно задать нулевое значение медианы, например p =signtest(x,0).
p = signtest(x,m) функция позволяет провести двусторонний знаковый тест на равенство медианы выборки х значению m. Величина m должна быть задана как скаляр.
p = signtest(x,y) функция позволяет провести парный двусторонний знаковый тест нулевой гипотезы, состоящей в том, что медиана разностного распределения генеральных совокупностей из которых были сделаны выборки x, y равна нулю. Предполагается, что разностное генеральное распределение, из которого получена выборка (x-y), является произвольным и непрерывным законом. Объем выборок x и y должен быть одинаковым, т.е. length(x)= length(y).
Примечание: гипотеза о равенстве нулю медианы генерального разностного распределения не является эквивалентной гипотезе о равенстве медиан генеральных распределений, из которых были получены x, y. Функция signrank позволяет проверить первую, но не вторую из названных статистических гипотез.
[p,h] = signtest(...) функция возвращает значение уровня значимости р и результат проверки нулевой гипотезы h для значения ![]() равного 0,05. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза принимается если h=0 при ![]() . Если h=1, то нулевая гипотеза может быть отвергнута при
. Если h=1, то нулевая гипотеза может быть отвергнута при ![]() .
.
[p,h] = signtest(...,alpha) входной параметр alpha позволяет задать значение критического уровня значимости при проверке нулевой гипотезы. По умолчанию alpha=0,05.
[p,h,stats] = signtest(...) функция возвращает структуру stats содержащую одно или два поля:
1. stats.sign - значение знаковой статистики;
2. stats.zval - значение Z статистики. Эта статистика рассчитывается при большом объеме выборки и значение уровня значимости р будет рассчитано исходя из нормальной аппроксимации распределения статистики Z.
Примеры использования функции знакового теста на равенство нулю медианы выборки
Проверка равенства нулю медиан выборок распределенных по непрерывному закону равной вероятности с величинами математического ожидания равными 0 и 0,1. Объем выборки равен 10 элементам. Функция возвращает значение уровня значимости p.
>> x = unifrnd(-0.9,1.1,10,1);
>> p = signtest (x,0)
p =
1
>> x = unifrnd(-1,1,10,1);
>> p = signtest (x,0)
p =
0.7539
Проверка равенства заданному значению, 0,22, медиан выборок распределенных по нормальному закону с величинами математического ожидания равными 0 и 0,5. Объем выборки равен 35 элементам. Функция возвращает значение уровня значимости p и результат проверки нулевой гипотезы.
>> x = normrnd(0,1,35,1);
>> [p h] = signtest (x,0.22)
p =
0.1755
h =
0
>> x = normrnd(0.5,1,35,1);
>> [p h] = signtest (x,0.22)
p =
0.3105
h =
0
Проверка равенства заданному значению, 0,5, медианы выборки распределенной по нормальному закону с величиной математического ожидания равной 0,1. Объем выборки равен 15 элементам. Функция возвращает значение уровня значимости и результат проверки нулевой гипотезы. При проверке нулевой гипотезы критическое значение уровня значимости принимается равным 0,01. Графическое представление теста выполняется при помощи функции boxplot.
>> x = normrnd(0.1,1,15,1);
>> alpha = 0.01;
>> [p h] = signtest (x,0.5, alpha)
p =
9.7656e-004
h =
1
>> boxplot(x,1)
.jpg)
Проверка равенства заданному значению, 0,7, медиан нескольких выборок распределенных по нормальному закону с величинами математических ожиданий равными 0; 0,5; 1; 1,5. Объем выборок равен 15 элементам. Функция возвращает значение уровня значимости, результат проверки нулевой гипотезы и структуру stats. При проверке нулевой гипотезы критическое значение уровня значимости принимается равным 0,07. Графическое представление теста выполняется при помощи функции boxplot.
>> x1 = normrnd(0,1,15,1);
>> x2 = normrnd(0.5,1,15,1);
>> x3 = normrnd(1,1,15,1);
>> x4 = normrnd(1.5,1,15,1);
>> alpha = 0.07;
>> [p1 h1 stats1] = signtest (x1,0.7, alpha)
p1 =
0.3018
h1 =
0
stats1 =
sign: 5
>> [p2 h2 stats2] = signtest (x2,0.7, alpha)
p2 =
1
h2 =
0
stats2 =
sign: 7
>> [p3 h3 stats3] = signtest (x3,0.7, alpha)
p3 =
0.0074
h3 =
1
stats3 =
sign: 2
>> [p4 p4 stats4] = signtest (x4,0.7, alpha)
p4 =
0
p4 =
0
stats4 =
sign: 4
>> boxplot([x1 x2 x3 x4],1)
Зависимость величины уровня значимости от разницы между математическими ожиданиями генеральных совокупностей и объемом выборок распределенных по нормальному закону.
>> delta = 0:0.1:1;
>>n=10;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); p1(i) = signtest (x,0); end;
>> n=20;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); p2(i) = signtest (x,0); end;
>> n=50;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); p3(i) = signtest (x,0); end;
>> plot(delta,p1,'or',delta,p2,'+b',delta,p3,'.g')
>> grid on
.jpg)
Проверка равенства нулю медианы выборки из разностной генеральной совокупности (x-y). При проверке нулевой гипотезы критическое значение уровня значимости принимается равным 0,01. Функция возвращает значение уровня значимости p, результат проверки нулевой гипотезы h и структуру stats. Графическое представление теста выполняется при помощи функции boxplot.
>> x = normrnd(0,1,50,1);
>> y = normrnd(0.5,2, 50,1);
>> alpha = 0.01;
>> [p h stats] = signtest (x,y, alpha)
p =
0.0153
h =
0
stats =
sign: 16
>> boxplot([x-y,x,y],1)
.jpg)
ttest - t-test для одной выборки. Проверка гипотезы о равенстве (или неравенстве) математического ожидания выборки заданному значению при условии, что величина дисперсии неизвестна. Закон распределения выборки нормальный.
Синтаксис
h = ttest(x)
h = ttest(x,m)
h = ttest(x,y)
h = ttest(x,m,alpha)
h = ttest(x,m,alpha,tail)
[h,p,ci] = ttest(...)
[h,p,ci,stats] = ttest(...)
Описание
h = ttest(x) функция предназначена для проверки нулевой гипотезы состоящей в том, что выборка х получена из генеральной совокупности с нулевым средним. Проверка нулевой гипотезы выполняется на основе статистики t. Выборка x задается как вектор. Функция возвращает скаляр h, являющийся результатом проверки нулевой гипотезы для критического значения уровня значимости ![]() равного 0,05. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза принимается если h=0 при ![]() . Если h=1, то нулевая гипотеза может быть отвергнута для
. Если h=1, то нулевая гипотеза может быть отвергнута для ![]() . Предполагается, что выборка х получена из генеральной совокупности имеющей нормальное распределение с неизвестной дисперсией.
. Предполагается, что выборка х получена из генеральной совокупности имеющей нормальное распределение с неизвестной дисперсией.
h = ttest(x,m) функция предназначена для проверки нулевой гипотезы состоящей в том, что выборка х получена из нормальной генеральной совокупности с математическим ожиданием равным m. Проверка нулевой гипотезы выполняется на основе статистики t.
h = ttest(x,y) функция позволяет провести проверку нулевой гипотезы состоящей в том, что выборки x и y получены из генеральных совокупностей имеющих одинаковое среднее значение. Предполагается, что разница выборочных значений (x-y) будет соответствовать генеральной совокупности имеющей нормальное распределение с неизвестной дисперсией. Число элементов в векторах x и y должно быть одинаковым. Проверка нулевой гипотезы выполняется на основе статистики t.
h = ttest(...,alpha) входной параметр alpha позволяет задать значение критического уровня значимости для проверки нулевой гипотезы. По умолчанию alpha=0,05. Условие принятия нулевой гипотезы
![]()
где ![]() - критический уровень значимости;
- критический уровень значимости; ![]() - уровень значимости, соответствующий рассчитанной статистике t. Выбор величины
- уровень значимости, соответствующий рассчитанной статистике t. Выбор величины ![]() предоставлен исследователю. В большинстве практических случаев
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01. Статистика t рассчитывается из выражения
принимают равным 0,05; 0,01. Статистика t рассчитывается из выражения
![]()
где ![]() - выборочное среднее арифметическое,
- выборочное среднее арифметическое, ![]() - точечная несмещенная оценка среднего квадратического отклонения,
- точечная несмещенная оценка среднего квадратического отклонения, ![]() - объем выборки,
- объем выборки, ![]() . Уровень значимости
. Уровень значимости ![]() является вероятностью того, что случайная величина t примет значение равное или превышающее выборочное статистику t для используемой критической области. Распределение статистики t подчиняется закону Стьюдента.
является вероятностью того, что случайная величина t примет значение равное или превышающее выборочное статистику t для используемой критической области. Распределение статистики t подчиняется закону Стьюдента.
h = ttest(...,alpha,tail) входной параметр tail позволяет задать вид альтернативной гипотезы. Возможны три альтернативные гипотезы:
|
Значение tail |
Альтернативная гипотеза |
|
'both' |
Среднее по генеральной совокупности не равно нулю или значению m. Проверка гипотезы проводится для двусторонней критической области. Значение по умолчанию. |
|
'right' |
Среднее по генеральной совокупности больше нуля, или величины m. Проверка гипотезы проводится для правосторонней критической области. |
|
'left' |
Среднее по генеральной совокупности меньше нуля, или величины m. Проверка гипотезы проводится для левосторонней критической области. |
[h,p,ci,stats] = ttest(...) функция возвращает: 1. результат проверки нулевой гипотезы h для заданного критического уровня значимости; 2. уровень значимости p, соответствующий рассчитанному значению статистики t; 3. вектор границ доверительного интервала выборочного среднего арифметического ci для доверительной вероятности (1-alpha); 4. структуру stats содержащую следующие поля:
'tstat' - значение статистики t, рассчитанное по выборке;
'df' - число степеней свободы t;
'sd' - несмещенную точечную оценку среднего квадратического отклонения. Если выполняется парный тест для двух выборок, то точечная оценка среднего квадратического отклонения рассчитывается для выборки разностей (x-y).
Примеры использования функции проверки параметрической гипотезы о значении среднего арифметического при неизвестной дисперсии нормальной генеральной совокупности
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Объем выборки равен 10 элементам. Функция возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,10,1);
>> h = ttest(x)
h =
0
Проверка равенства единице среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0,5 и 2, по выборке х. Объем выборки равен 25 элементам. Функция возвращает результат проверки нулевой гипотезы h. Графическое представление распределение значений выборки выполняется при помощи функции histfit.
>> x = normrnd(0.5,2,25,1);
>> h = ttest(x)
h =
0
>> histfit(x,7)
>> grid on
.jpg)
Проверка нулевой гипотезы состоящей в том, что выборки x и y получены из генеральных совокупностей имеющих одинаковое среднее значение, равное нулю. x распределена по нормальному закону, y по равномерному закону. Выборки x, y имеют разное значение дисперсии. Функция возвращает результат проверки нулевой гипотезы h. Графическое представление распределений значений выборок x, y, (x-y) выполняется при помощи функции ksdensity.
>> x=normrnd(0,1,30,1);
>> y=unifrnd(-1,1,30,1);
>> h = ttest(x,y)
h =
1
>> [fx,xx] = ksdensity(x);
>> [fy,xy] = ksdensity(y);
>> [f_xy,x_xy] = ksdensity(x-y);
>> plot(xx,fx,'r',xy,fy,'g',x_xy,f_xy, 'b')
>> grid on
.jpg)
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Проверка нулевой гипотезы выполняется для критического значения уровня значимости равного 0,01. Объем выборки равен 15 элементам. Функция возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,15,1);
>> h = ttest(x,0.01)
h =
0
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Проверка нулевой гипотезы выполняется для критического значения уровня значимости равного 0,01. В качестве альтернативной гипотезы принимается предположение, что среднее по генеральной совокупности больше нуля. Проверка гипотезы проводится для правосторонней критической области. Объем выборки равен 15 элементам. Функция возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,15,1);
>> h = ttest(x,0,0.01,'right')
h =
0
Примечание: при задании трех и более входных параметров, если проверяется гипотеза на равенство нулю среднего генеральной совокупности, необходимо явно указать m=0 для второго параметра.
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Проверка нулевой гипотезы выполняется для критического значения уровня значимости равного 0,01. В качестве альтернативной гипотезы принимается предположение, что среднее по генеральной совокупности больше нуля. Проверка гипотезы проводится для правосторонней критической области. Объем выборки равен 15 элементам. Функция возвращает: результат проверки нулевой гипотезы h для заданного критического уровня; уровень значимости p соответствующий рассчитанному значению статистики t; вектор границ доверительного интервала среднего арифметического ci для доверительной вероятности (1-alpha); структуру stats.
>> [h,p,ci,stats] = ttest(x,0,0.01,'right')
h =
0
p =
0.7655
ci =
-0.8499 Inf
stats =
tstat: -0.7443
df: 14
sd: 0.9771
Зависимость величины уровня значимости от математического ожидания и объема выборок, распределенных по нормальному закону. Проверяется нулевая гипотеза на равенство нулю средних генеральных совокупностей. Дисперсия выборок равна 1.
>> delta = 0:0.1:1;
>>n=10;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); [h,p1(i),ci,stats] = ttest(x,0); end;
>> n=20;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); [h,p2(i),ci,stats] = ttest(x,0); end;
>> n=50;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); [h,p3(i),ci,stats] = ttest(x,0); end;
>> plot(delta,p1,'or',delta,p2,'+b',delta,p3,'.g')
>> grid on
.jpg)
ttest2 - t-test для двух выборок. Проверка гипотезы о равенстве (или неравенстве) математических ожиданий двух выборок при условии, что величины дисперсий выборок неизвестны и равны. Закон распределения выборки нормальный.
Синтаксис
h = ttest2(x,y)
[h,significance,ci]= ttest2(x,y,alpha)
[h,significance,ci,stats]= ttest2(x,y,alpha)
[...] =ttest2(x,y,alpha,tail)
h = ttest2(x,y,alpha,tail,'unequal')
Описание
h = ttest2(x,y) функция предназначена для проверки нулевой гипотезы состоящей в том, что выборки х, получены из генеральных совокупностей имеющих нормальное распределение с одинаковыми средними значениями. Предполагается, что средние квадратические отклонения генеральных совокупностей неизвестны и равны между собой. Векторы x и y могут иметь разное количество элементов. Выходной параметр h является результатом проверки нулевой гипотезы для критического значения уровня значимости ![]() равного 0,05. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза принимается если h=0 при ![]() . Если h=1,то нулевая гипотеза может быть отвергнута для
. Если h=1,то нулевая гипотеза может быть отвергнута для ![]() . Проверка нулевой гипотезы выполняется на основе статистики t.
. Проверка нулевой гипотезы выполняется на основе статистики t.
Условие принятия нулевой гипотезы
![]() ,
,
где![]() -критический уровень значимости;
-критический уровень значимости; ![]() - уровень значимости, соответствующийрассчитанной статистике t. Выбор величины
- уровень значимости, соответствующийрассчитанной статистике t. Выбор величины ![]() предоставлен исследователю. В большинстве практических случаев
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01. Статистика t рассчитывается из выражения
принимают равным 0,05; 0,01. Статистика t рассчитывается из выражения
.gif) ,
,
где ![]() ,
, ![]() - средние арифметические рассчитанные по выборкам x, y;
- средние арифметические рассчитанные по выборкам x, y; ![]() - точечная оценка объединенного среднегоквадратического отклонения;
- точечная оценка объединенного среднегоквадратического отклонения; ![]() ,
, ![]() - объем выборок x, y,
- объем выборок x, y, ![]() ,
, ![]() . Уровень значимости
. Уровень значимости ![]() является вероятностью того, что случайная величина примет значение равное или превышающее выборочноезначение статистики t для используемой критической области. Статистика t подчиняется распределению Стьюдента.
является вероятностью того, что случайная величина примет значение равное или превышающее выборочноезначение статистики t для используемой критической области. Статистика t подчиняется распределению Стьюдента.
[h,significance,ci]= ttest2(x,y,alpha) функция возвращает: 1. результат проверки нулевой гипотезы h для заданного критического уровня значимости; 2. уровень значимости significance, соответствующий выборочному значению статистики t; 3. вектор границ доверительного интервала разности выборочных средних арифметических ci для доверительной вероятности (1-alpha). Дополнительный входной параметр alpha позволяет задать величину критического уровня значимости для проверки нулевой гипотезы. Значение по умолчанию alpha=0,05.
[h,significance,ci,stats] = ttest2(x,y,alpha) выходной параметр stats является структурой со следующими полями:
-
tstat - значение статистики t, рассчитанной по выборке;
-
df - число степеней свободы t;
-
'sd' - точечная оценка объединенного среднего квадратического отклонения, если дисперсии выборок равны, в противном случае 'sd' представляет собой вектор выборочных средних квадратических отклонений.
[...] = ttest2(x,y,alpha,tail) входной параметр tail позволяет задать вид альтернативной гипотезы. Возможны три альтернативные гипотезы:
|
Значение tail |
Альтернативная гипотеза |
|
'both' |
Средние генеральных совокупностей не равны |
|
'right' |
Среднее генеральной совокупности |
|
'left' |
Среднее генеральной совокупности |
h =ttest2(x,y,alpha,tail,'unequal') входной параметр 'unequal' предназначен для проверки нулевой гипотезы, если выборки x, получены из генеральных совокупностей, имеющих нормальное распределение с разными дисперсиями. Эта задача известна как проблема Беренса-Фишера. Для ее решения в ttest2 используется аппроксимация Саттервейта при определении эффективного числа степеней свободы.
Примеры использования функции проверки параметрической гипотезы о разности значений средних арифметических двух выборок
Проверка нулевой гипотезы, состоящей в том, что выборки х, y получены из генеральных совокупностей имеющих нормальное распределение с одинаковым средними значениями, для критического уровня значимости 0,05. Дисперсия выборок равна единице. Выборки x, y имеют равный объем. Графическое представление выборок x, y выполняется при помощи функции непараметрического сглаживания ksdensity. ttest2 возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,15,1);
>> y = normrnd(0,1,15,1);
>> h = ttest2(x,y)
h =
0
>> [fx,xx] = ksdensity(x);
>> [fy,xy] = ksdensity(y);
>> plot(xx,fx,'r',xy,fy,'g')
>> grid on
.jpg)
Проверка нулевой гипотезы, состоящей в том, что выборки х, y получены из генеральных совокупностей имеющих нормальное распределение с одинаковыми средними значениями, для критического уровня значимости 0,05. Дисперсия выборок равна единице. Выборки x, y имеют равный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних ci.
>> x = normrnd(0,1,15,1);
>> y = normrnd(0,1,15,1);
>> [h,significance,ci]= ttest2(x,y)
h =
0
significance =
0.6343
ci =
-1.2187 0.7552
Проверка нулевой гипотезы, состоящей в том, что выборки х, получены из генеральных совокупностей имеющих нормальное распределение с одинаковым средними значениями, для критического уровня значимости 0,05. Дисперсия выборок равна единице. Выборки x, имеют разный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних арифметических ci.
>> x = normrnd(0,1,15,1);
>> y = normrnd(0,1,20,1);
>> [h,significance,ci]= ttest2(x,y)
h =
0
significance =
0.5589
ci =
-0.5619 1.0214
Проверка нулевой гипотезы, состоящей в том, что выборки х, получены из генеральных совокупностей имеющих нормальное распределение с одинаковым средними значениями, для критического уровня значимости alpha=0,01. Дисперсия выборок равна единице. Выборки x, y имеют разный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних арифметических ci.
>> x = normrnd(0,1,15,1);
>> y = normrnd(0,1,20,1);
>> [h,significance,ci]= ttest2(x,y,0.01)
h =
0
significance =
0.3646
ci =
-1.2813 0.6363
Проверка нулевой гипотезы, состоящей в том, что выборки х, получены из генеральных совокупностей имеющих нормальное распределение с одинаковым средними значениями, для критического уровня значимости alpha=0,01. Альтернативная гипотеза принимается для соотношения среднего погенеральной совокупности x больше среднего по y, ![]() . Проверка гипотезы проводится для правосторонней критической области. Дисперсия выборок равна единице. Выборки x, y имеют разный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних арифметических ci; структуру stats.
. Проверка гипотезы проводится для правосторонней критической области. Дисперсия выборок равна единице. Выборки x, y имеют разный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних арифметических ci; структуру stats.
>> x = normrnd(0,1,15,1);
>> y = normrnd(0,1,20,1);
>> alpha= 0.01;
>>[h,significance,ci,stats] = ttest2(x,y,alpha,'right')
h =
0
significance =
0.5599
ci =
-0.8481 Inf
stats =
tstat: -0.1519
df: 33
sd: 0.9562
Проверка нулевой гипотезы, состоящей в том, что выборки х, получены из генеральных совокупностей имеющих нормальное и равномерное распределения с одинаковым средними значениями, для критического уровня значимости alpha=0,01. Альтернативная гипотеза принимается для соотношения среднего по генеральной совокупности x больше среднего по y, ![]() . Проверка гипотезы проводится для правосторонней критической области. Выборки x, y имеют разный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних арифметических ci; структуру stats.
. Проверка гипотезы проводится для правосторонней критической области. Выборки x, y имеют разный объем. Функция возвращает результат проверки нулевой гипотезы h; уровень значимости significance, соответствующий рассчитанному значению статистики t; вектор границ(1-alpha) доверительного интервала разности выборочных средних арифметических ci; структуру stats.
>> x = normrnd(0,1,15,1);
>> y = unifrnd(-1,1,20,1);
>> alpha= 0.01;
>> tail='right';
>>[h,significance,ci,stats] = ttest2(x,y,alpha,tail,'unequal')
h =
0
significance =
0.9467
ci =
-1.2356 Inf
stats =
tstat: -1.6883
df: 20.3251
sd: [1.0252 0.5649]
Зависимость величины уровня значимости от разности средних генеральных совокупностей, распределенных по нормальному закону, и объема выборок. Проверяется нулевая гипотеза на равенство средних двух генеральных совокупностей. Дисперсия выборок равна 1.
>> delta= 0:0.2:1;
>> n=10;
>> y =normrnd(0,1,n,1);
>> for i=1:length(delta)x = normrnd(delta(i),1,n,1); [h, p1(i),ci,stats] = ttest2(x,y); end;
>> n=20;
>> y = normrnd(0,1,n,1);
>> fori=1:length(delta) x = normrnd(delta(i),1,n,1); [h, p2(i),ci,stats] = ttest2(x,y);end;
>> n=50;
>> y =normrnd(0,1,n,1);
>> fori=1:length(delta) x = normrnd(delta(i),1,n,1); [h, p3(i),ci,stats] = ttest2(x,y);end;
>> plot(delta,p1,'or',delta,p2,'+b',delta,p3,'.g')
>> grid on
.jpg)
ztest - Z-тест. Проверка гипотезы о равенстве (или неравенстве) математического ожидания выборки заданному значению при условии, что известна величина дисперсии. Закон распределения выборки нормальный.
Синтаксис
h = ztest(x,m,sigma)
h = ztest(x,m,sigma,alpha)
[h,sig,ci,zval] = ztest(x,m,sigma,alpha,tail)
Описание
h = ztest(x,m,sigma) функция предназначена для проверки нулевой гипотезы состоящей в том, что выборка х получена из генеральной совокупности имеющей нормальное распределение со средним m и средним квадратическим отклонением sigma. Проверка нулевой гипотезы выполняется на основе статистики Z. Выборка x задается как вектор. Функция возвращает скаляр h, являющийся результатом проверки нулевой гипотезы для критического уровня значимости ![]() равного 0,05. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза принимается если h=0 при ![]() . Если h=1, то нулевая гипотеза может быть отвергнута для
. Если h=1, то нулевая гипотеза может быть отвергнута для ![]() .
.
h = ztest(x,m,sigma,alpha) входной параметр alpha позволяет задать значение критического уровня значимости для проверки нулевой гипотезы. По умолчанию alpha=0,05. Условие принятия нулевой гипотезы
![]() ,
,
где ![]() - критический уровень значимости;
- критический уровень значимости; ![]() - уровень значимости, соответствующий выборочной статистике Z. Выбор величины
- уровень значимости, соответствующий выборочной статистике Z. Выбор величины ![]() предоставлен исследователю. В большинстве практических случаев
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01. Статистика Z рассчитывается из выражения
принимают равным 0,05; 0,01. Статистика Z рассчитывается из выражения
![]() ,
,
где ![]() - выборочное среднее арифметическое,
- выборочное среднее арифметическое, ![]() - точечная несмещенная оценка среднего квадратического отклонения,
- точечная несмещенная оценка среднего квадратического отклонения, ![]() - объем выборки,
- объем выборки, ![]() . Уровень значимости
. Уровень значимости ![]() является вероятностью того, что случайная величина примет значение равное или превышающее выборочное значение статистики Z для используемой критической области.
является вероятностью того, что случайная величина примет значение равное или превышающее выборочное значение статистики Z для используемой критической области.
[h,sig,ci,zval] = ztest(x,m,sigma,alpha,tail) дополнительный входной параметр tail позволяет задать вид альтернативной гипотезы. Возможны три альтернативные гипотезы:
|
Значение tail |
Альтернативная гипотеза |
|
'both' |
Среднее генеральной совокупности не равно m, |
|
'right' |
Среднее генеральной совокупности больше m, |
|
'left' |
Среднее генеральной совокупности меньше m, |
Выходными параметрами функции являются: 1. результат проверки нулевой гипотезы h для заданного критического уровня значимости; 2. уровень значимости sig, соответствующий выборочному значению статистики Z; 3. вектор границ доверительного интервала выборочного среднего арифметического ci для доверительной вероятности (1-alpha); 4. значение выборочной статистики Z, zval.
Примеры использования функции проверки параметрической гипотезы о значении среднего арифметического при известной дисперсии нормальной генеральной совокупности
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Объем выборки равен 10 элементам. Функция возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,10,1);
>> h = ztest(x,0,1)
h =
1
Проверка равенства 0,5 среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0,5 и 2, по выборке х. Объем выборки равен 25 элементам. Функция возвращает результат проверки нулевой гипотезы h. Графическое представление распределения значений выборки выполняется при помощи функции histfit.
>> x = normrnd(0.5,2,25,1);
>> h = ztest(x,0.5,2)
h =
0
>> histfit(x,7)
>> grid on
.jpg)
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Проверка нулевой гипотезы выполняется для критического значения уровня значимости равного 0,01. Объем выборки равен 15 элементам. Функция возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,15,1);
>> alpha=0.01;
>> h = ztest(x,0,1,alpha)
h =
0
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Проверка нулевой гипотезы выполняется для критического значения уровня значимости равного 0,01. В качестве альтернативной гипотезы принимается предположение, что среднее по генеральной совокупности больше нуля. Проверка гипотезы проводится для правосторонней критической области. Объем выборки равен 15 элементам. Функция возвращает результат проверки нулевой гипотезы h.
>> x = normrnd(0,1,15,1);
>> alpha=0.01;
>> h = ztest(x,0,1,alpha,'right')
h =
0
Проверка равенства нулю среднего арифметического генеральной совокупности, распределенной по нормальному закону с математическим ожиданием и дисперсией равными 0 и 1, по выборке х. Проверка нулевой гипотезы выполняется для критического значения уровня значимости равного 0,01. В качестве альтернативной гипотезы принимается предположение, что среднее по генеральной совокупности больше нуля. Проверка гипотезы проводится для правосторонней критической области. Объем выборки равен 15 элементам. Выходными параметрами функции являются: результат проверки нулевой гипотезы h для заданного критического уровня значимости; уровень значимости sig, соответствующий рассчитанному значению статистики Z; вектор границ (1-alpha) доверительного интервала среднего арифметического ci; значение выборочной статистики Z, zval.
>> x = normrnd(0,1,15,1);
>> alpha=0.01;
>> [h,sig,ci,zval] = ztest(x,0,1,alpha,'right')
h =
0
sig =
0.4234
ci =
-0.5508 Inf
zval =
0.1933
Зависимость величины уровня значимости от математического ожидания генеральной совокупности, распределенной по нормальному закону, и объема выборки. Проверяется нулевая гипотеза на равенство нулю средних генеральных совокупностей. Дисперсия выборок равна 1.
>> delta = 0:0.1:1;
>>n=10;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); [h,p1(i),ci,zval] = ztest(x,0,1); end;
>> n=20;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); [h,p2(i),ci,zval] = ztest(x,0,1); end;
>> n=50;
>> for i=1:length(delta) x = normrnd(delta(i),1,n,1); [h,p3(i),ci,zval] = ztest(x,0,1); end;
>> plot(delta,p1,'or',delta,p2,'+b',delta,p3,'.g')
>> grid on
.jpg)
Вид распределения статистики Z. Генеральная совокупность распределена по нормальному закону с нулевым математическим ожиданием и единичной дисперсией. Объем выборки равен 5. Количество выборок равно 25.
>> m=0;
>> sigma=1;
>> n=5;
>> N=25;
>> for i=1:N x = normrnd(m,sigma,n,1); [h,p,ci,zval(i)] = ztest(x,m,sigma); end;
>> histfit(zval)
>> grid on
.jpg)
jbtest - Тест на соответствие выборки нормальному распределению с неопределенными параметрами нормального распределения.
Синтаксис
H = jbtest(X)
H = jbtest(X,alpha)
[H,P,JBSTAT,CV] = jbtest(X,alpha)
Описание
H = jbtest(X) функция предназначена для выполнения теста Ярки-Бера на непротиворечие распределения генеральной совокупности значений слуайной величины нормальному закону по выборкеX.X задается как вектор. Функция возвращает скалярH, являющийся результатом проверки нулевой гипотезы для критического уровня значимости ![]() равного 0,05. Нулевая гипотеза состоит в том, что распределение генеральной совокупности значений случайной величины не противоречит нормальному закону. Альтернативная гипотеза теста Ярки-Бера состоит в том, что распределение генеральной совокупности противоречит нормальному закону. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза состоит в том, что распределение генеральной совокупности значений случайной величины не противоречит нормальному закону. Альтернативная гипотеза теста Ярки-Бера состоит в том, что распределение генеральной совокупности противоречит нормальному закону. Нулевая гипотеза принимается если h=0 при ![]() . ЕслиH=1, то нулевая гипотеза может быть отвергнута при
. ЕслиH=1, то нулевая гипотеза может быть отвергнута при ![]() .
.
Тест Ярки-Бера используется в случаях, когда неизвестны среднее арифметическое и дисперсия генеральной совокупности. Проверка нулевой гипотезы основана на расчете оценок коэффициентов асимметрии и эксцесса по выборке Х. В случае справедливости нулевой гипотезы выборочное значение коэффициента асимметрии должно быть приблизительно равно нулю, а выборочное значение эксцесса - трем. Следует отметить, что в отечественной литературе коэффициент эксцесса определяется по формуле ![]() , где
, где ![]() - коэффициент эксцесса,
- коэффициент эксцесса, ![]() - точечная оценка среднего квадратического отклонения,
- точечная оценка среднего квадратического отклонения, ![]() - четвертый эмпирический центральный момент,
- четвертый эмпирический центральный момент, ![]() - выборочное среднее арифметическое,
- выборочное среднее арифметическое, ![]() - вектор выборочных значений. Следовательно, коэффициент эксцесса нормального закона будет равен 0.
- вектор выборочных значений. Следовательно, коэффициент эксцесса нормального закона будет равен 0.
При проведении теста Ярки-Бера определяются отклонения выборочных коэффициентов асимметрии и эксцесса, относительно ожидаемых значений при условии справедливости нулевой гипотезы для заданного объема выборки. В качестве меры отклонений выборочных значений коэффициентов асимметрии и эксцесса используется статистика хи-квадрат. Тест Ярки-Бера используется при большом объеме выборки Х. При малом объеме выборки используется тест Лиллиефорса.
H = jbtest(X,alpha) входной параметр alpha позволяет задать значение критического уровня значимости для проверки нулевой гипотезы. По умолчаниюalpha=0,05. Условие принятия нулевой гипотезы
|
|
(1) |
где ![]() - критический уровень значимости;
- критический уровень значимости; ![]() - уровень значимости, соответствующий выборочной статистике хи-квадрат. Выбор величины
- уровень значимости, соответствующий выборочной статистике хи-квадрат. Выбор величины ![]() предоставлен исследователю. В большинстве практических случаев
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
[H,P,JBSTAT,CV] = jbtest(X,alpha) выходными параметрами функции являются: 1. результат проверки нулевой гипотезы H для заданного критического уровня значимости; 2. уровень значимости P, соответствующий выборочному значению статистики хи-квадрат; 3. значение выборочной статистики хи-квадратJBSTAT; 4. критическое значение статистики хи-квадратCV. ВеличинаCV служит для проверки нулевой гипотезы. Если JBSTAT<CV, то нулевая гипотеза может быть принята, в противном случае принимается альтернативная гипотеза. Таким образом, указанное условие является альтернативным по отношению к (1).
Примеры использования функции теста Ярки-Бера на непротиворечие распределения генеральной совокупности нормальному закону
Тест Ярки-Бера на непротиворечие нормальному закону генеральной совокупности, распределенной по нормальному закону, по выборочным значениям. Объем выборки - 25 элементов. Функция возвращает результат проверки нулевой гипотезы. Графическое представление распределения выборочных значений выполняется с помощью функции histfit.
>> x = normrnd(0,1,25,1);
>> H = jbtest(x)
H =
0
>> histfit(x,7)
>> grid on
.jpg)
Тест Ярки-Бера на непротиворечие нормальному закону генеральной совокупности, распределенной по нормальному закону, по выборочным значениям. Объем выборки - 30 элементов. Функция возвращает результат проверки нулевой гипотезы для критического значения уровня значимости 0,01. Графическое представление распределения выборочных значений выполняется с помощью функции >qqplot.
>> x = normrnd(0,1,30,1);
>> alpha=0.01;
>> H = jbtest(x,alpha)
H =
0
>> qqplot(x)
>> grid on
.jpg)
Тест Ярки-Бера на непротиворечие нормальному закону генеральной совокупности, распределенной по нормальному закону, по выборочным значениям. Распределение генеральной совокупности представляет композицию нормального и равномерного законов. Объем выборки - 30 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01. Графическое представление распределения выборочных значений выполняется с помощью функции >qqplot.
>> x = normrnd(0,1,30,1)+unifrnd(-2,1,30,1);
>> alpha=0.01;
>> H = jbtest(x,alpha)
H =
0
>> qqplot(x)
>> grid on
.jpg)
Тест Ярки-Бера на непротиворечие нормальному закону генеральной совокупности, распределенной по нормальному закону, по выборочным значениям. Распределение генеральной совокупности представляет композицию нормального и равномерного законов. Объем выборки - 30 элементов. Графическое представление распределения выборочных значений выполняется с помощью функции >qqplot. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01; уровень значимостиP соответствующий, выборочному значению статистики хи-квадрат; значение выборочной тестовой статистики хи-квадрат; критическое значение статистики хи-квадрат.
>> x = normrnd(0,1,30,1)+unifrnd(-3,3,30,1);
>> alpha=0.01;
>> [H,P,JBSTAT,CV] = jbtest(x,alpha)
H =
0
P =
0.4221
JBSTAT =
1.7249
CV =
9.2103
Зависимость величины уровня значимости при проверке нулевой гипотезы от объема выборки и дисперсии равномерного закона, как составляющей композиции законов распределения случайной величиныx. Распределение генеральной совокупности является композицией нормального и равномерного законов. Параметры нормальной составляющей постоянны и равны: математическое ожидание - 0, дисперсия - 1. Математическое ожидание равномерной составляющей постоянно и принято равным нулю.
>> sigma = 0:0.1:3/1.73;
>>n=10;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p1(i),JBSTAT,CV] = jbtest(x); end;
>> n=20;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p2(i),JBSTAT,CV] = jbtest(x); end;
>> n=50;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p3(i),JBSTAT,CV] = jbtest(x); end;
>> plot(sigma,p1,'or', sigma,p2,'+b', sigma,p3,'.g')
>> grid on
.jpg)
Вид распределения выборочной статистики хи-квадрат. Распределение генеральной совокупности формируется как композиция нормального и равномерного законов. Объем выборки равен 20 элементам. Количество выборок равно 25. Графическая оценка соответствия нормальному закону выборочной статистики выполняется с помощью функции>qqplot.
>> m_norm=0;
>> sigma_norm =1;
>> m_unif=0;
>> sigma_unif=3/1.73;
>> n=20;
>> N=25;
>> for i=1:N x = normrnd(m_norm, m_norm,n,1)+unifrnd(m_unif-1.73*sigma_unif,m_unif+1.73*sigma_unif,n,1); [H,P,JBSTAT(i),CV] = jbtest(x);end;
>> qqplot(JBSTAT)
>> grid on
.jpg)
kstest - Тест Колмогорова-Смирнова на соответствие выборки заданному распределению
Синтаксис
H = kstest(X)
H = kstest(X,cdf)
H = kstest(X,cdf,alpha,tail)
[H,P,KSSTAT,CV] = kstest(X,cdf,alpha,tail)
Описание
H = kstest(X) функция предназначена для выполнения теста Комогорова-Смирнова на непротиворечие распределения значений генеральной совокупности значений случайной величины стандартному нормальному закону (нормальному закону с нулевым математическим ожиданием и единичной дисперсией) по выборке X. X задается как вектор. Функция возвращает скаляр H, являющийся результатом проверки нулевой гипотезы для критического уровня значимости ![]() равного 0,05. Нулевая гипотеза состоит в том, что распределение генеральной совокупности не противоречит стандартному нормальному закону. Альтернативная гипотеза теста Комогорова-Смирнова состоит в том, что распределение генеральной совокупности противоречит стандартному нормальному закону. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза состоит в том, что распределение генеральной совокупности не противоречит стандартному нормальному закону. Альтернативная гипотеза теста Комогорова-Смирнова состоит в том, что распределение генеральной совокупности противоречит стандартному нормальному закону. Нулевая гипотеза принимается если h=0 при ![]() . Если H=1, то нулевая гипотеза может быть отвергнута для
. Если H=1, то нулевая гипотеза может быть отвергнута для ![]() .
.
При проведении теста Комогорова-Смирнова для серии заданных значений случайной величины х сравнивается доля выборочных значений Х(:)<x с долей ожидаемых значений, согласно стандартному нормальному закону. Максимальная разность между ожидаемой долей и долей значений Х(:)<x по выборке используется как выборочная статистика Комогорова-Смирнова. Т.е., выборочная статистика рассчитывается из выражения
![]() .
.
где ![]() - доля выборочных значений меньших заданного значения х, Х(:)<x;
- доля выборочных значений меньших заданного значения х, Х(:)<x; ![]() - значение кумулятивной функции стандартного нормального распределения для заданного х.
- значение кумулятивной функции стандартного нормального распределения для заданного х.
H = kstest(X,cdf) функция предназначена для выполнения теста Комогорова-Смирнова на непротиворечие распределения генеральной совокупности значений случайной величины произвольному закону распределения вероятностей cdf по выборке Х. Входной параметр cdf задается как матрица с размерностью m×2, где m - число заданных значений случайной величины х. Первый столбец матрицы cdf соответствует заданным значениям случайной величины х. Второй столбец матрицы cdf рассчитывается по кумулятивной теоретической функции распределения в точках х. Задание cdf в указанном виде является рекомендуемым. Если cdf будет определена как вектор, без столбца соответствующего х, значение ![]() будет рассчитано методом интерполяции. Значения х должны находиться в интервале между минимальным и максимальным значениями первого столбца матрицы cdf. Если второй аргумент задан как пустой вектор или матрица, cdf=[ ], в качестве теоретического распределения будет использован стандартный нормальный закон.
будет рассчитано методом интерполяции. Значения х должны находиться в интервале между минимальным и максимальным значениями первого столбца матрицы cdf. Если второй аргумент задан как пустой вектор или матрица, cdf=[ ], в качестве теоретического распределения будет использован стандартный нормальный закон.
Тест Комогорова-Смирнова используется в случаях, когда явно задана теоретическая функция распределения и ее параметры. Если параметры закона распределения рассчитываются по выборочным значениям, использование теста Комогорова-Смирнова приведет к существенной погрешности. Поэтому, если необходимо выполнить проверку на непротиворечие генеральной совокупности нормальному закону с неопределенными параметрами, необходимо использовать тест Лиллиефорса.
H = kstest(X,cdf,alpha,tail) входной параметр alpha позволяет задать значение критического уровня значимости для проверки нулевой гипотезы. По умолчанию alpha=0,05. Условие принятия нулевой гипотезы
|
|
(1) |
где ![]() - критический уровень значимости;
- критический уровень значимости; ![]() - уровень значимости, соответствующий выборочной статистике Колмогорова-Смирнова. Выбор величины
- уровень значимости, соответствующий выборочной статистике Колмогорова-Смирнова. Выбор величины ![]() предоставлен исследователю. В большинстве практических случаев
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
Входной параметр tail предназначен для задания вида альтернативной гипотезы. Если tail=0, альтернативной гипотезой является ![]() и проверка гипотезы выполняется для двусторонней критической области. tail=-1 соответствует альтернативной гипотезе
и проверка гипотезы выполняется для двусторонней критической области. tail=-1 соответствует альтернативной гипотезе ![]() . tail=1 соответствует альтернативной гипотезе
. tail=1 соответствует альтернативной гипотезе ![]() . Значение по умолчанию tail=0. Выражение для расчета статистики Комогорова-Смирнова будет зависеть от вида альтернативной гипотезы:
. Значение по умолчанию tail=0. Выражение для расчета статистики Комогорова-Смирнова будет зависеть от вида альтернативной гипотезы:
|
Значение параметра tail |
Выражение для расчета статистики Комогорова-Смирнова |
|
tail=0 |
|
|
tail=-1 |
|
|
tail=1 |
|
[H,P,KSSTAT,CV] = kstest(X,cdf,alpha,tail) выходными параметрами функции являются: 1. результат проверки нулевой гипотезы H для заданного критического уровня значимости; 2. уровень значимости P, соответствующий выборочному значению статистики Комогорова-Смирнова; 3. значение выборочной статистики Комогорова-Смирнова KSSTAT; 4. критическое значение статистики Комогорова-Смирнова CV. Величина CV служит для проверки нулевой гипотезы. Если KSSTAT<CV, то нулевая гипотеза может быть принята, в противном случае принимается альтернативная гипотеза. Таким образом, указанное условие является альтернативным по отношению к (1). Если выходной параметр CV=NaN, то величина P будет рассчитана по асимптотической формуле, и для определения значений H будет использовано выражение (1) вместо условия KSSTAT<CV.
Примеры использования функции теста Комогорова-Смирнова на непротиворечие распределения генеральной совокупности заданному закону распределения
Тест Комогорова-Смирнова на непротиворечие генеральной совокупности стандартному нормальному закону. Объем выборки - 15 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,05. Графическое представление распределения выборочных значений выполняется с помощью функции histfit.
>> x = normrnd(0,1,15,1);
>> H = kstest (x)
H =
0
>> histfit(x,5)
>> grid on
.jpg)
Тест Комогорова-Смирнова на непротиворечие генеральной совокупности нормальному закону с математическим ожиданием равным 1 и средним квадратическим отклонением равным 2. Объем выборки - 35 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,05.
>> x = normrnd(1,2,35,1);
>> X=-6:0.5:8;
>> Y=normcdf(X,1,2);
>> cdf=[X' Y'];
>> H = kstest(x,cdf)
H =
0
Тест Комогорова-Смирнова на непротиворечие генеральной совокупности закону Вейбулла с параметром масштаба равным 1 и коэффициентом формы 2. Выборка распределена по равномерному закону. Объем выборки - 40 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01.
>> x = unifrnd(0,4,40,1);
>> X=0:0.5:4;
>> Y=wblcdf(X,1,2);
>> cdf=[X' Y'];
>> H = kstest(x,cdf,0.01)
H =
1
Тест Комогорова-Смирнова на непротиворечие генеральной совокупности нормальному закону с математическим ожиданием равным 0 и средним квадратическим отклонением равным 2. Объем выборки - 30 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,02. Альтернативная гипотеза соответствует ![]() .
.
>> x = normrnd(0,2,30,1);
>> X=-6:0.5:6;
>> Y=normcdf(X,0,2);
>> cdf=[X' Y'];
>> tail=-1;
>> H = kstest(x,cdf,0.02,tail)
H =
0
Тест Комогорова-Смирнова на непротиворечие генеральной совокупности закону Вейбулла с параметром масштаба равным 1 и коэффициентом формы 2. Выборка распределена по равномерному закону. Объем выборки - 40 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01; уровень значимости, соответствующий выборочному значению статистики Комогорова-Смирнова; значение выборочной статистики Комогорова-Смирнова; критическое значение статистики Комогорова-Смирнова.
>> x = unifrnd(0,4,40,1);
>> X=0:0.5:4;
>> Y=wblcdf(X,1,2);
>> cdf=[X' Y'];
>> [H,P,KSSTAT,CV] = kstest(x,cdf,0.01)
H =
1
P =
4.6349e-011
KSSTAT =
0.5415
CV =
0.2521
Вид распределения выборочной статистики Комогорова-Смирнова. Распределение генеральной совокупности формируется как композиция нормального и равномерного законов. Нулевая гипотеза состоит в непротиворечии генеральной совокупности стандартному нормальному закону. Объем выборки равен 50 элементам. Количество выборок равно 25. Графическая оценка соответствия нормальному закону выборочной статистики Комогорова-Смирнова выполняется при помощи функции qqplot.
>> m_norm=0;
>> sigma_norm =1;
>> m_unif=0;
>> sigma_unif=3/1.73;
>> n=50;
>> N=25;
>> for i=1:N x = normrnd(m_norm, m_norm,n,1)+unifrnd(m_unif-1.73*sigma_unif,m_unif+1.73*sigma_unif,n,1); [H,P,KSSTAT(i),CV] = kstest(x);end;
>> qqplot(KSSTAT)
>> grid on
.jpg)
Зависимость величины уровня значимости при проверке нулевой гипотезы от объема выборки и дисперсии равномерного закона, как составляющей композиции законов распределения случайной величины x. Распределение генеральной совокупности формируется как композиция нормального и равномерного законов. Нулевая гипотеза состоит в непротиворечии генеральной совокупности стандартному нормальному закону. Параметры нормальной составляющей постоянны и равны: математическое ожидание - 0, дисперсия - 1. Математическое ожидание равномерной составляющей постоянно и принято равным нулю.
>> sigma = 0:0.1:3/1.73;
>>n=20;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p1(i),KSSTAT,CV] = kstest(x); end;
>> n=30;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p2(i),KSSTAT,CV] = kstest(x); end;
>> n=50;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p3(i),KSSTAT,CV] = kstest(x); end;
>> plot(sigma,p1,'or', sigma,p2,'+b', sigma,p3,'.g')
>> grid on
.jpg)
kstest2 - Тест Колмогорова-Смирнова на соответствие распределений двух выборок
Синтаксис
H = kstest2(X1,X2)
H = kstest2(X1,X2,alpha,tail)
[H,P,KSSTAT] = kstest2(...)
Описание
H = kstest2(X1,X2) функция позволяет выполнить тест Комогорова-Смирнова для сравнения законов распределения двух генеральных совокупностей значений случайных величин по выборкам X1, X2. Выборки X1, X2 задаются как векторы с размерностями n1, n2 соответственно. Функция возвращает скаляр H, являющийся результатом проверки нулевой гипотезы для критического значения уровня значимости ![]() равного 0,05. Нулевая гипотеза состоит в том, что две генеральные совокупности значений случайных величин распределены по одному и тому же непрерывному закону. Альтернативная гипотеза состоит в том, что две генеральные совокупности значений случайных величин распределены по разным непрерывным законам. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза состоит в том, что две генеральные совокупности значений случайных величин распределены по одному и тому же непрерывному закону. Альтернативная гипотеза состоит в том, что две генеральные совокупности значений случайных величин распределены по разным непрерывным законам. Нулевая гипотеза принимается если h=0 при ![]() . Если H=1, то нулевая гипотеза может быть отвергнута при
. Если H=1, то нулевая гипотеза может быть отвергнута при ![]() .
.
При проведении теста Комогорова-Смирнова для серии заданных значений случайной величины х сравниваются доли выборочных значений, удовлетворяющих условиям Х1(:)≤x и Х2(:)≤x. Максимальная разность между указанными долями выборочных значений, соответствующих условиям Х1(:)≤x и Х2(:)≤x, используется как выборочная статистика Комогорова-Смирнова. Т.е., статистику Комогорова-Смирнова можно представить следующим образом
![]() ,
,
где ![]() ,
, ![]() - доли выборочных значений, удовлетворяющих условиям Х1(:)≤x и Х2(:)≤x соответственно. Элементы векторов X1(i), X2(i) равные NaN считаются как пропущенные значения и игнорируются при расчете.
- доли выборочных значений, удовлетворяющих условиям Х1(:)≤x и Х2(:)≤x соответственно. Элементы векторов X1(i), X2(i) равные NaN считаются как пропущенные значения и игнорируются при расчете.
H = kstest2(X1,X2,alpha,tail) входной параметр alpha позволяет задать значение критического уровня значимости для проверки нулевой гипотезы. По умолчанию alpha=0,05. Условие принятия нулевой гипотезы
|
|
(1) |
где ![]() - критический уровень значимости;
- критический уровень значимости; ![]() - уровень значимости, соответствующий выборочной статистике Колмогорова-Смирнова. Выбор величины
- уровень значимости, соответствующий выборочной статистике Колмогорова-Смирнова. Выбор величины ![]() предоставлен исследователю. В большинстве практических случаев
предоставлен исследователю. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
Входной параметр tail предназначен для задания вида альтернативной гипотезы. Если tail=0, альтернативной гипотезой является ![]() и проверка выполняется для двусторонней критической области. tail=-1 соответствует альтернативной гипотезе
и проверка выполняется для двусторонней критической области. tail=-1 соответствует альтернативной гипотезе![]() . tail=1 соответствует альтернативной гипотезе
. tail=1 соответствует альтернативной гипотезе![]() . Значение по умолчанию tail=0. Выражение для расчета выборочной статистики Комогорова-Смирнова будет зависеть от вида альтернативной гипотезы:
. Значение по умолчанию tail=0. Выражение для расчета выборочной статистики Комогорова-Смирнова будет зависеть от вида альтернативной гипотезы:
|
Значение параметра tail |
Выражение для расчета статистики Комогорова-Смирнова |
|
tail=0 |
|
|
tail=-1 |
|
|
tail=1 |
|
[H,P,KSSTAT] = kstest2(...) выходными параметрами функции являются: 1. результат проверки нулевой гипотезы H для заданного критического уровня значимости; 2. уровень значимости P, соответствующий выборочному значению статистики Комогорова-Смирнова; 3. значение выборочной статистики Комогорова-Смирнова KSSTAT.
Асимптотическое значение уровня значимости Р имеет минимальную погрешность при больших объемах выборок Х1 и Х2, или если выполняется условие (n1*n2)/(n1+n2)>=4.
Примеры использования функции теста Комогорова-Смирнова для сравнения законов распределения двух генеральных совокупностей значений случайных величин
Тест Комогорова-Смирнова на согласие распределений двух генеральных совокупностей по выборочным значениям. Объем выборок - 15 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,05. Графическое представление распределений выборочных значений выполняется с помощью функции непараметрического сглаживания ksdensity.
>> x = normrnd(0,1,15,1);
>> y = normrnd(0,1,15,1);
>> H = kstest2(x,y)
H =
0
>> [fx,xx] = ksdensity(x);
>> [fy,xy] = ksdensity(y);
>> plot(xx,fx,'r',xy,fy,'g')
>> grid on
.jpg)
Тест Комогорова-Смирнова на согласие распределений двух генеральных совокупностей по выборочным значениям. Выборки распределены по нормальному и равномерному законам с одинаковыми математическими ожиданиями и дисперсиями. Объем выборок - 20 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,05. Графическое представление распределений выборочных значений выполняется с помощью функции непараметрического сглаживания ksdensity.
>> x = normrnd(0,1,20,1);
>> y = unifrnd(-1.73,1.73,20,1);
>> H = kstest2(x,y)
H =
0
>> [fx,xx] = ksdensity(x);
>> [fy,xy] = ksdensity(y);
>> plot(xx,fx,'r',xy,fy,'g')
>> grid on
.jpg)
Тест Комогорова-Смирнова на согласие распределений двух генеральных совокупностей по выборочным значениям. Выборки распределены по нормальному и равномерному законам с различными математическими ожиданиями и дисперсиями. Объем выборок - 30 и 50 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,02. Графическое представление распределений выборочных значений выполняется с помощью функции непараметрического сглаживания ksdensity.
>> x = normrnd(0,1,30,1);
>> y = unifrnd(-5,5,50,1);
>> H = kstest2(x,y,0.02)
H =
1
>> [fx,xx] = ksdensity(x);
>> [fy,xy] = ksdensity(y);
>> plot(xx,fx,'r',xy,fy,'g')
>> grid on
.jpg)
Тест Комогорова-Смирнова на согласие распределений двух генеральных совокупностей по выборочным значениям. Альтернативная гипотеза принимается равной ![]() . Выборки распределены по нормальному и равномерному законам с различными математическими ожиданиями и дисперсиями. Объем выборок - 30 и 50 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,02.
. Выборки распределены по нормальному и равномерному законам с различными математическими ожиданиями и дисперсиями. Объем выборок - 30 и 50 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,02.
>> x = normrnd(0,1,30,1);
>> y = unifrnd(-5,5,50,1);
>> tail=-1;
>> H = kstest2(x,y,0.02,tail)
H =
0
Тест Комогорова-Смирнова на согласие распределений двух генеральных совокупностей по выборочным значениям. Выборки распределены по нормальному и равномерному законам с различными математическими ожиданиями и дисперсиями. Объем выборок - 10 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01; уровень значимости, соответствующий выборочной статистике Комогорова-Смирнова; значение выборочной статистики Комогорова-Смирнова.
>> x = normrnd(0,1,10,1);
>> y = unifrnd(-5,5,10,1);
>> [H,P,KSSTAT] = kstest2(x,y,0.01)
H =
0
P =
0.1108
KSSTAT =
0.5000
Вид распределения выборочной статистики Комогорова-Смирнова при проверке нулевой гипотезы для генеральных совокупностей, распределенных по нормальному и равномерному законам. Объем выборок равен 50 элементам. Количество выборок равно 25. Графическая оценка соответствия выборочной статистики Комогорова-Смирнова нормальному закону выполняется с помощью функции qqplot.
>> m_norm=0;
>> sigma_norm =1;
>> m_unif=0;
>> sigma_unif=3/1.73;
>> n=50;
>> N=25;
>> for i=1:N x = normrnd(m_norm, m_norm,n,1); y=unifrnd(m_unif-1.73*sigma_unif,m_unif+1.73*sigma_unif,n,1); [H,P,KSSTAT(i)] = kstest2(x,y);end;
>> qqplot(KSSTAT)
>> grid on
.jpg)
lillietest - Тест на соответствие выборки нормального распределения рассчитываются исходя из значений элементов в выборке.
Синтаксис
H = lillietest(X)
H = lillietest(X,alpha)
[H,P,LSTAT,CV] = lillietest(X,alpha)
Описание
H = lillietest(X) функция предназначена для выполнения теста Лиллиефорса на непротиворечие распределения генеральной совокупности значений случайной величины нормальному закону по выборке Х. X задается как вектор. Функция возвращает скаляр H, являющийся результатом проверки нулевой гипотезы для критического уровня значимости ![]() равного 0,05. Нулевая гипотеза состоит в том, что распределение генеральной совокупности значений случайной величины не противоречит нормальному закону с неизвестными средним арифметическим и дисперсией. Альтернативная гипотеза теста Лиллиефорса состоит в том, что распределение генеральной совокупности значений случайной величины противоречит нормальному закону. Нулевая гипотеза принимается если h=0 при
равного 0,05. Нулевая гипотеза состоит в том, что распределение генеральной совокупности значений случайной величины не противоречит нормальному закону с неизвестными средним арифметическим и дисперсией. Альтернативная гипотеза теста Лиллиефорса состоит в том, что распределение генеральной совокупности значений случайной величины противоречит нормальному закону. Нулевая гипотеза принимается если h=0 при ![]() . Если H=1, то нулевая гипотеза может быть отвергнута для
. Если H=1, то нулевая гипотеза может быть отвергнута для ![]() .
.
Тест Лиллиефорса основан на сравнении эмпирического распределения частот выборки Х и нормального закона. Параметры нормального закона рассчитываются по выборке Х. Тест Лиллиефорса аналогичен критерию Колмогорова-Смирнова, но в последнем случае параметры нормального закона предполагаются известными.
H = lillietest(X,alpha) входной параметр alpha позволяет задать значение критического уровня значимости для проверки нулевой гипотезы. По умолчанию alpha=0,05. Условие принятия нулевой гипотезы
|
|
(1) |
где ![]() - критический уровень значимости;
- критический уровень значимости; ![]() - уровень значимости, соответствующий выборочной тестовой статистике. Выбор величины
- уровень значимости, соответствующий выборочной тестовой статистике. Выбор величины ![]() предоставлен исследователю и должен изменяться в пределах от 0,01 до 0,2. В большинстве практических случаев
предоставлен исследователю и должен изменяться в пределах от 0,01 до 0,2. В большинстве практических случаев ![]() принимают равным 0,05; 0,01.
принимают равным 0,05; 0,01.
[H,P,LSTAT,CV] = lillietest(X,alpha) выходными параметрами функции являются: 1. результат проверки нулевой гипотезы H для заданного критического уровня значимости; 2. уровень значимости P соответствующий выборочному значению тестовой статистики; 3. значение выборочной тестовой статистики LSTAT; 4. критическое значение тестовой статистики CV. Величина CV служит для проверки нулевой гипотезы. Если LSTAT <CV, то нулевая гипотеза может быть принята, в противном случае принимается альтернативная гипотеза. Таким образом, указанное условие является альтернативным по отношению к (1). Величина P определяется методом линейной интерполяции по таблице Лиллиефорса на основе тестовой статистики LSTAT. Если LSTAT выходит за пределы табличных значений, функция возвращает P=NaN, но H показывает возможность принятия нулевой гипотезы.
Примеры использования функции теста Лиллиефорса на непротиворечие распределения генеральной совокупности значений случайной величины нормальному закону
Тест Лиллиефорса на непротиворечие нормальному закону распределения генеральной совокупности по выборочным значениям. Объем выборки - 10 элементов. Функция возвращает результат проверки нулевой гипотезы. Графическое представление распределения выборочных значений выполняется с помощью функции histfit.
>> x = normrnd(0,1,10,1);
>> H = lillietest(x)
H =
0
>> histfit(x,5)
>> grid on
.jpg)
Тест Лиллиефорса на непротиворечие нормальному закону распределения генеральной совокупности по выборочным значениям. Объем выборки - 15 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01. Графическое представление распределения выборочных значений выполняется с помощью функции qqplot.
>> x = normrnd(0,1,15,1);
>> alpha=0.01;
>> H = lillietest(x,alpha)
H =
0
>> qqplot(x)
>> grid on
.jpg)
Тест Лиллиефорса на непротиворечие нормальному закону распределения генеральной совокупности по выборочным значениям. Распределение генеральной совокупности является композицией нормального и равномерного законов. Объем выборки - 10 элементов. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01. Графическое представление распределения выборочных значений выполняется при помощи функции qqplot.
>> x = normrnd(0,1,10,1)+unifrnd(-2,1,10,1);
>> alpha=0.01;
>> H = lillietest(x,alpha)
H =
0
>> qqplot(x)
>> grid on
.jpg)
Тест Лиллиефорса на непротиворечие нормальному закону распределения генеральной совокупности по выборочным значениям. Распределение генеральной совокупности является композицией нормального и равномерного законов. Объем выборки - 15 элементов. Графическое представление распределения выборочных значений выполняется с помощью функции qqplot. Функция возвращает результат проверки нулевой гипотезы для критического уровня значимости 0,01; уровень значимости P, соответствующий значению выборочной тестовой статистики; значение выборочной тестовой статистики; критическое значение тестовой статистики.
>> x = normrnd(0,1,15,1)+unifrnd(-3,3,15,1);
>> alpha=0.01;
>> [H,P,LSTAT,CV] = lillietest(x,alpha)
H =
0
P =
NaN
LSTAT =
0.1198
CV =
0.2570
Зависимость величины уровня значимости при проверке нулевой гипотезы от объема выборки и дисперсии равномерного закона, как составляющей композиции законов распределения случайной величины x. Распределение генеральной совокупности является композицией нормального и равномерного законов. Параметры нормальной составляющей постоянны и равны: математическое ожидание - 0, дисперсия - 1. Математическое ожидание равномерной составляющей постоянно и принято равным нулю.
>> sigma = 0:0.1:3/1.73;
>>n=5;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p1(i),JBSTAT,CV] = lillietest(x); end;
>> n=10;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p2(i),JBSTAT,CV] = lillietest(x); end;
>> n=20;
>> for i=1:length(sigma) x = normrnd(0,1,n,1)+unifrnd(-1.73*sigma(i), 1.73*sigma(i),n,1); [H,p3(i),JBSTAT,CV] = lillietest(x); end;
>> plot(sigma,p1,'or', sigma,p2,'+b', sigma,p3,'.g')
>> grid on
.jpg)
Вид распределения выборочной тестовой статистики. Распределение генеральной совокупности формируется как композиция нормального и равномерного законов. Объем выборки равен 10 элементам. Количество выборок равно 25. Графическая оценка соответствия нормальному закону выборочной статистики выполняется с помощью функции qqplot.
>> m_norm=0;
>> sigma_norm =1;
>> m_unif=0;
>> sigma_unif=3/1.73;
>> n=10;
>> N=25;
>> for i=1:N x = normrnd(m_norm, m_norm,n,1)+unifrnd(m_unif-1.73*sigma_unif,m_unif+1.73*sigma_unif,n,1); [H,P,JBSTAT(i),CV] = lillietest(x);end;
>> qqplot(JBSTAT)
>> grid on
.jpg)
ksdensity - Подгонка функции плотности вероятности по экспериментальным данным
Синтаксис
[f,xi] = ksdensity(x)
f = ksdensity(x,xi)
[f,xi,u] = ksdensity(...)
[...] = ksdensity(...,'param1',val1,'param2',val2,...)
Описание
[f,xi] = ksdensity(x) функция предназначена для расчета значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания по исходной выборке х. Выборка исходных данных х задается как вектор. Выходные параметры f, xi будут представлены как векторы на 100 элементов каждый. Вектор xi рассчитывается с постоянным шагом. В качестве базовой функции сглаживания используется функция плотности нормального закона.
f = ksdensity(x,xi) функция предназначена для расчета значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания по исходной выборке х. Значения случайной величины, в которых рассчитывается функция плотности вероятности, задается как входной параметр xi.
[f,xi,u] = ksdensity(...) функция возвращает значение функции плотности вероятности f в точках xi и величину окна сглаживания u.
[...] = ksdensity(...,'param1',val1,'param2',val2,...) дополнительные входные параметры, 'param1', 'param2',:, задаются в виде пары "название параметра, значение" и позволяют:
|
Название параметра 'param' |
Функции и возможные значения val дополнительных входных параметров |
|
'censoring' |
Цензурирование входных данных. Значение параметра задается как вектор логических значений. Число элементов вектора значений val и исходной выборки х должно совпадать. Элементы цензурирующего вектора соответствуют элементам исходной выборки х. По умолчанию цензурирование не предусмотрено. |
|
'kernel' |
Выбор базовой функции сглаживания. Предусмотрены 4 базовых функции: 'normal', 'box', 'triangle', 'epanechinikov'. По умолчанию в качестве базовой функции сглаживания принимается функция распределения плотности вероятности нормального закона 'normal'. Пользователь может определить базовую функцию сглаживания в виде m-функции. В этом случае в качестве значения параметра используется указатель на функцию или соотвествующее строковое значение, например 'normpdf или 'normpdf'. Входным аргументом базовой m-функции должен быть массив значений случайной величины, в которых будут рассчитываться значения функции плотности вероятности. M-функция должна возвратить массив значений базовой функции сглаживания той же размерности, что и массив входных значений. |
|
'npoints' |
Число элементов в выходных векторах f и xi. Значение по умолчанию - 100. Шаг между значениями в векторе xi постоянный. |
|
'support' |
Интервал, на котором определена функция распределения плотности вероятностей. Возможны следующие значения параметра:'unbounded' - функция плотности вероятностей определена для всех вещественных чисел (значение по умолчанию); 'positive' - функция плотности вероятностей определена для положительных вещественных чисел; Значение параметра задается как двух элементный вектор, содержащий нижнюю и верхнюю границы интервала на котором определена функция плотности вероятностей. |
|
'weights' |
Вектор весовых значений элементов исходной выборки х. Размерность вектора весовых значений и исходной выборки должна совпадать. По умолчанию веса значений исходной выборки принимаются одинаковыми. |
|
'width' |
Параметр определяет величину окна сглаживания. По умолчанию величина окна сглаживания принимается оптимальной для нормальной базовой функции сглаживания. Позднее выходной параметр u может быть использован для уменьшения величины окна сглаживания. Уменьшение окна сглаживание позволяет показать более мелкие детали распределения выборки, например две моды находящиесяна малом расстоянии. |
Примеры использования функции расчета значений функции распределения плотности вероятностей методом непараметрического сглаживания
Расчет значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания исходной выборки х.
>> x = normrnd(0,1,100,1);
>> [f,xi] = ksdensity(x);
>> plot(xi,f)
>> grid on
.jpg)
>> histfit(x,7)
>> grid on
.jpg)
Расчет значений функции распределения плотности вероятностей f методом непараметрического сглаживания исходной выборки х. Значения случайной величины xi задаются как входной аргумент.
>> x = normrnd(0,1,100,1);
>> xi=-3:0.1:3;
>> f = ksdensity(x, xi);
>> plot(xi,f)
>> grid on
.jpg)
Расчет значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания исходной выборки х. Кроме f, xi функция возвращает величину окна сглаживания u.
>> x = weibrnd(2,1,100,1);
>> [f,xi,u] = ksdensity(x)
f =
Columns 1 through 9
0.0030 0.0059 0.0111 0.0199 0.0343 0.0567 0.0897 0.1363 0.1987
::::::::::::::..
Columns 91 through 99
0.0154 0.0120 0.0089 0.0063 0.0043 0.0027 0.0017 0.0010 0.0005
Column 100
0.0003
xi =
Columns 1 through 9
-0.4462 -0.4130 -0.3799 -0.3467 -0.3136 -0.2804 -0.2473 -0.2141 -0.1809
:::::::::
Columns 91 through 99
2.5376 2.5707 2.6039 2.6370 2.6702 2.7034 2.7365 2.7697 2.8028
Column 100
2.8360
u =
0.1519
>> plot(xi,f)
>> grid on
.jpg)
Расчет значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания исходной выборки х. Кроме f, xi функция возвращает величину окна сглаживания u. Дополнительный входной параметр определяет цензурирование исходной выборки.
>> x = weibrnd(2,1,100,1);
>> cen=unidrnd(2,100,1)-1;
>> [f,xi,u] = ksdensity(x, 'censoring',cen);
>> plot(xi,f)
>> grid on
.jpg)
Расчет значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания исходной выборки х. Кроме f, xi функция возвращает величину окна сглаживания u. Дополнительные входные параметры: 'censoring' - определяет цензурирование исходной выборки и 'kernel' - изменяет базовую функцию сглаживания.
>> x = weibrnd(2,1,100,1);
>> cen=unidrnd(2,100,1)-1;
>> [f,xi,u] = ksdensity(x, 'censoring',cen,'kernel','triangle');
>> plot(xi,f)
>> grid on
.jpg)
Расчет значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания исходной выборки х. Дополнительный входной параметр 'npoints' задает число значений f и xi.
>> x = normrnd(0,1,100,1);
>> [f,xi] = ksdensity(x,'npoints',10);
>> plot(xi,f,'+')
>> grid on
.jpg)
Расчет значений функции распределения плотности вероятностей f для значений случайной величины xi методом непараметрического сглаживания исходной выборки х. Дополнительные входные параметры задают пределы непараметрического сглаживания - 'support' и вектор весовых значений 'weights'.
>> x = weibrnd(2,1,100,1);
>> wet =unidrnd(10,100,1);
>> [f,xi] = ksdensity(x, 'support', 'positive', 'weights',wet);
>> plot(xi,f)
>> grid on
.jpg)
Исследование распределения вероятностей автомобилей по расходу топлива. Исходные данные получены из файла carsmall. Дополнительный входной параметр 'width' определяет величину окна сглаживания. Уменьшение значения 'width' позволяет определить на функции распределения плотности вероятностей более мелкие детали. Исходное значение 'width' получается как выходной аргумент функции ksdensity.
>> cars = load('carsmall','MPG','Origin');
>> MPG = cars.MPG;
>> Origin = cars.Origin;
>> [f,x] = ksdensity(MPG);
>> [f,x,u] = ksdensity(MPG);
>> plot(x,f)
>> title('Density estimate for MPG')
>> hold on
>> [f,x] = ksdensity(MPG,'width',u/3);
>> plot(x,f,'r');
>> [f,x] = ksdensity(MPG,'width',u*3);
>> plot(x,f,'g');
>> legend('default width','1/3 default','3*default')
>> hold off
>> grid on
.jpg)
rsmdemo - Интерактивное моделирование химическое реакции и нелинейный регрессионный анализ
Синтаксис
rsmdemo
Описание
rsmdemo - функция предназначена для демонстрации методов: D-оптимального планирования эксперимента, регрессинного анализа и представления поверхности отклика для множества факторов, оценки параметров нелинейной модели Хогена. Демонстрация работы с указанными методами проводится на примере химической реакции 3 реагентов. Целью планирования эксперимента является поиск максимума коэффициента выхода полезного продукта. Функция rsmdemo основана на графическом интерфейсе с пользователем.
Интерфес состоит из 3-х графических окон:
-
окна моделирования параметров химической реакции (рис. 1),
-
окна результатов измерений (рис. 2),
-
окна результатов эксперимента (рис. 3).
Назначение элементов окна моделирования параметров химической реакции:
-
Строки ввода Hydrogen, n-Pentane, Isopentane и соотвествующие им полосы проктуки позволяют установить давление водорода, n-пентана и изопентана в химическом реакторе;
-
Строка ввода Reaction Rate отображает результат моделирования коэффициента выхода полезного продукта;
-
Строка ввода Runs Left показывает количество проведенных опытов. Значения изменяются от 13 до 0;
-
Кнопка Run предназначена для моделирования одного опыта - расчета коэффициента выхода полезного продукта при заданных значениях Hydrogen, n-Pentane, Isopentane с учетом случайных отклонений;
-
Кнопка Export позволяет создать в рабочей среде matlab матричную переменную значений независимых переменных и вектор коэффициента выхода полезного продукта. Названия переменных задаются в диалоговом окне после выбора кнопки, по умолчанию reactants и rate.
-
Кнопки Close и Help предназначены для закрытия окна и вызова помощи.

Рис. 1. Окно моделирования параметров химической реакции
Окно результатов измерений отображает результаты моделирования для опытов, проводимых пользователем по своему усмотрению в виде таблицы. Кнопка Analyze вызывает графическое окно функции rstool для представления результатов регрессионного анализа. Меню Plot позволяет построить графики зависимости коэффициента выхода реакции от величины давления каждого из компонентов.
Рис. 2. Окно результатов измерений
Окно результатов эксперимента предназначено для D-оптимального планирования и моделирования результатов 3-х факторного эксперимента в автоматическом режиме. Кнопка Do Experiment запускает процесс планирования и моделирования результатов эксперимента. Кнопка Response Surface вызывает графическое окно функции rstool для отображения результатов регрессионного анализа. Кнопка Nonlinear Model вызывает графическое окно функции nlintool для отображения результатов регрессионного анализа по модели Хогена-Ватсона. Меню Plot позволяет построить графики зависимости коэффициента выхода реакции от величины давления каждого из компонентов.
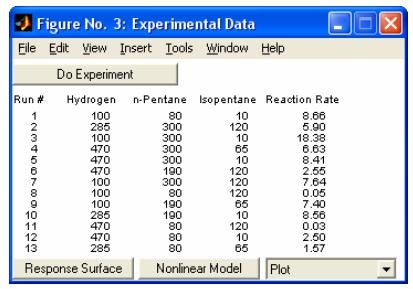
Рис. 3. Окно результатов эксперимента
Функция rsmdemo позволяет сравнить эффективность применения метода планирования эксперимента по сравнению со случайным выбором параметров и проведением опытов при одинаковом их количестве. Под случайным выбором параметров реакции понимается проведение пассивных наблюдений за характеристиками химической реакции или поиск оптимальных условий реакции по усмотрению пользователя.
На первом этапе демонстрации пользователь в окне моделирования параметров химической реакции устанавливает значения давления реагентов в химическом реакторе. При нажатии кнопки Run выполняется расчет коэффициента выхода полезного продукта. Результат расчета отображается в строке ввода Reaction Rate. При расчете коэффициента выхода учитываются как значения давления реагентов, так и воздействие случайных факторов. Принимается, что распределение значений коэффициента выхода подчиняется нормальному закону с параметрами: математическое ожидание 1, среднее квадратическое отклонение 0,05. Расчет коэффициента выхода y выполняется по формуле
|
y=1.25*(p2 - p3/1.5183)./(1+0.064*p1+0.0378*p2+0.1326*p3)*normrnd(1,0.05), |
(1) |
где p1 - давление водорода, p2 - давление n-пентана, p3 - давление изопентана. Таким образом, при одинаковых величинах факторов значения коэффициента выхода полезного продукта будут изменяться от опыта к опыту.
Установленные значения факторов и результаты моделирования коэффициента выхода отображаются в окне результатов измерений. Пользователь должен провести 13 опытов.
По окончании моделирования опытов пользователь выполняет регрессионный анализ экспериментальных данных. С этой целью в окне результатов измерений предусмотрены кнопка Analyze и меню Plot. При выборе кнопки Analyze для проведения регрессионного анализа вызывается функция rstool: rstool(x,y,[],[],xname,yname). Технология графического представления данных функции rstool предназначена для построения зависимости одной независимой переменной от множества независимых переменных (3 и более). Регрессионный анализ при помощи функции rstool предусматривает возможности выбора линейной, не полной квадратической, полной квадратической моделей и линейной модели с эффектами взаимодействий факторов. Выбор команды в меню Plot позвляет получить декартовы графики зависимостей коэффициента выхода от давления каждого их компонентов в отдельности.
Второй этап включает 2 фазы: D-оптимальное планирование и моделирование результатов эксперимента по формуле (1). Планирования и моделирование экспермента проводится в автоматическом режиме после нажатия кнопки Do Experiment. Формирование матрицы значений факторов проводится с использованием алгоритма изменения координат для 3 факторов, 13 опытов и полной квадратической модели. С этой целью используется функция: settings=cordexch(3,13,'q'). Согласно полученной матрице уровней фактров по формуле (1) проводится расчет значений коэффициента выхода полезного продукта. Матрица уровней факторов и вектор значений коэффициента выхода выводся в табличном виде в окне результатов эксперимента.
По окончании моделирования опытов пользователь выполняет регрессионный анализ экспериментальных данных. С этой целью в окне результатов эксперимента предусмотрены кнопки Response Surface, Nonlinear Model и меню Plot. При выборе кнопки Response Surface вызывается функция rstool и анализ проводится аналогично первому этапу. Кнопка Nonlinear Model позволяет в качестве модели химической рекции использовать функцию Хогена-Ватсона:
y = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3).
Расчет коэффициентов модели Хогена-Ватсона выполняется с использованием функции nlintool: nlintool(x,y,'hougen',beta0,[],xname,yname). Способ отображения результатов регрессионного анализа функции nlintool аналогична rstool.
Пример использования функции rsmdemo
>> rsmdemo
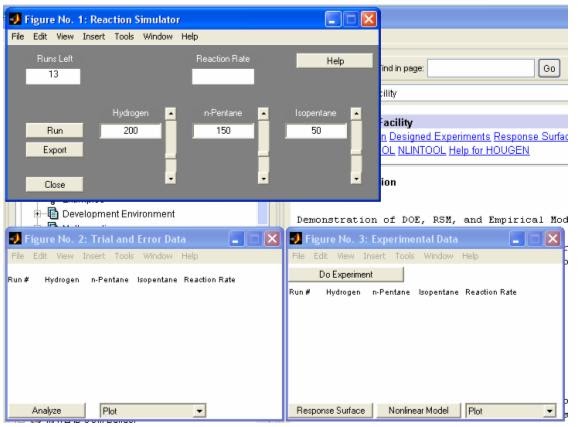
Моделирование пассивных наблюдений за химической реакцией. Результаты 13 наблюдений приведены на следующем рисунке
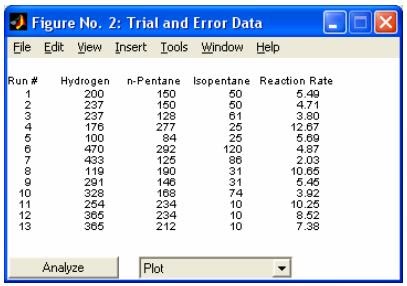
Регрессионный анализ полученных данных для линейной модели с эффектами взаимодействий (кнопка Analyze)
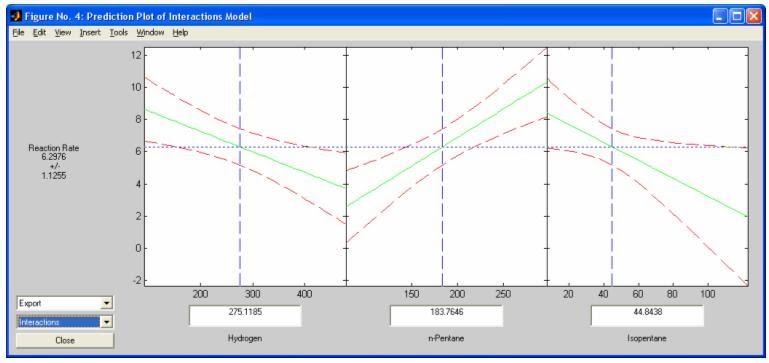
Зависимость коэффициента выхода полезного продукта от давления водорода (Меню Plot, Reaction Rate vs. Hydrogen)
Планирование и моделирование результатов эксперимента (Кнопка Do Experiment)
Регрессионный анализ результатов эксперимента для линейной модели с эффектами взаимодействий (кнопка Response Surface)
Зависимость коэффициента выхода полезного продукта от давления водорода (Меню Plot, Reaction Rate vs. Hydrogen)
Регрессионный анализ результатов эксперимента для модели Хогена-Ватсона (кнопка Nonliner Model)
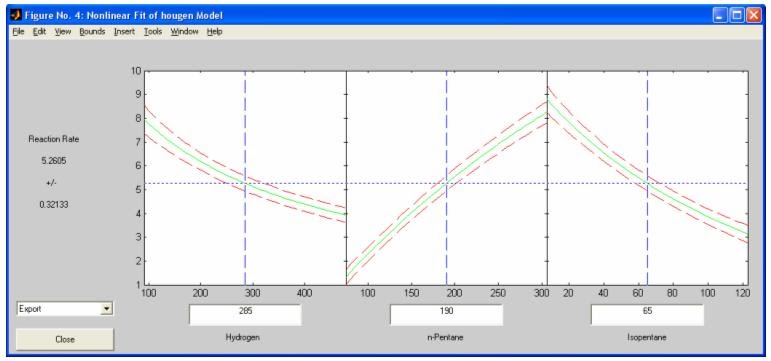
Из анализа приведенных графиков следует, что применение D-оптимального планирования эксперимента обеспечивает получение оценки коэффициентов уравнения регресии с меньшей дисперсией (меньшим доверительным интервалом). Испольование модели Хогена-Ватсона обеспечивает меньшую погрешность при описании процесса протекания химической реакции.
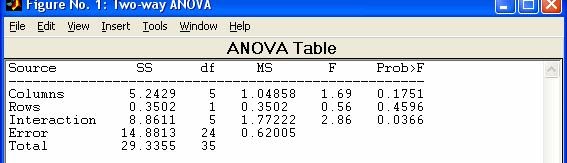
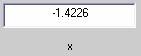
Комментарии