Идентификация системы на основе измерений АЦП/ЦАП USB-6009
Contents
- Схема цепочки для снятия напряжения с конденсатора
- Задаем параметры
- Переходный процесс по аналитической формуле
- Снимаем экспериментальные данные
- Схема измерения
- Загружаем данные эксперимента и обрезаем их
- Подготавливаем данные для System Identification и Parameter Estimation
- Сравниваем аналитическое решение и экспериментальное
- Системная идентификация
- Убираем постоянную составляющую
- Сравниваем аналитически полученные параметры и на основе идентификации
- Оптимизация модели
- Parameter Estimation
- Выбираем параметры для оценки
- Результат подгонки параметров
- Что дальше?
- Выводы
- Похожий пример в справочном руководстве
- Использованные материалы
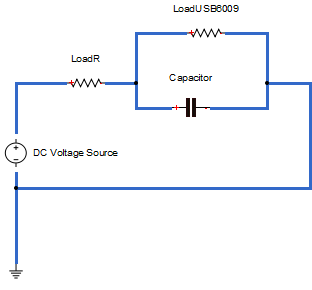
Схема цепочки для снятия напряжения с конденсатора
Будем подавать напряжение постоянного тока на RC цепочку. Измерение будем проводить при помощи аналогового входа USB-6009
Задаем параметры
Берем значения из документации, обозначения на элементах, дополнительно измеряем мультиметром
- R1 - сопротивление нагрузки, LoadR
- R2 - сопротивление на аналоговом входе, LoadUSB6009
- C1 - сопротивление емкости, Capacitor, K50-35
- Vs - напряжение источника, DC Voltage Source
- Vf - установившееся напряжение после переходного процесса
- Vc - напряжение на конденсаторе С1, функция от времени
- tau -
 - постоянная времени переходного процесса
- постоянная времени переходного процесса
C1=10e-6;% Номинал - 10 мкф, допуск +- 20%, Измерение - 10.3 мкФ R2=288E3;% USB6009, измеренное значение мультиметром 288 кОм R1=100E3;% 5 последовательных сопротивлений с номиналом по 20кОм. % Измерение показало 99,9 кОМ Vs=7.08;% Измерения - 7.08 V0=0.0;
Переходный процесс по аналитической формуле
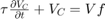
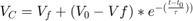
Сумма токов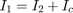
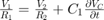
Так как Vs=V1+V2 и V2=Vc, то
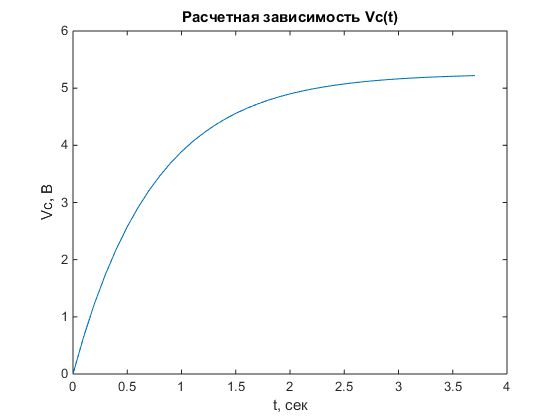
tau=C1/(1/R1+1/R2) K=(1/R1)/(1/R1+1/R2) Vf=K*Vs Vc=@(t)(Vf+(V0-Vf)*exp(-t/tau)) ta=0:0.1:5*tau; vc=Vc(ta); figure plot(ta,vc); title('Расчетная зависимость Vc(t)'); xlabel('t, сек'); ylabel('Vc, В')
tau =
0.7423
K =
0.7423
Vf =
5.2553
Vc =
@(t)(Vf+(V0-Vf)*exp(-t/tau))
Снимаем экспериментальные данные
Подаем и снимаем сигнал с USB 6009
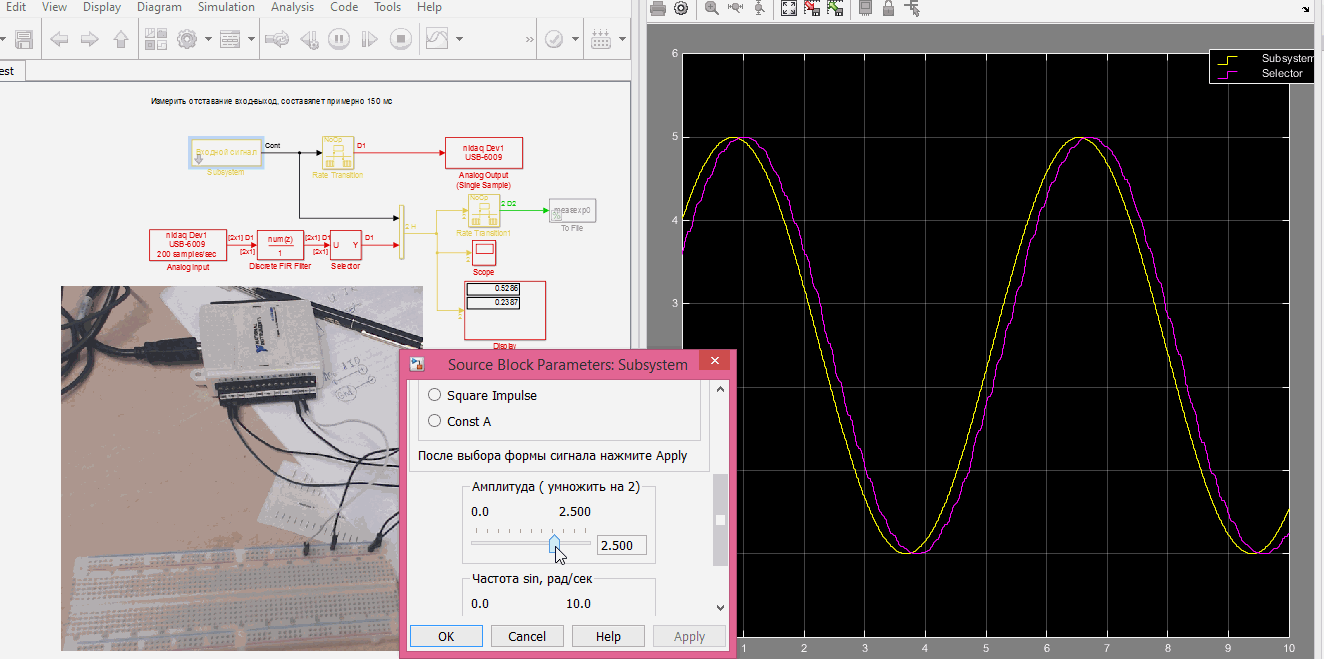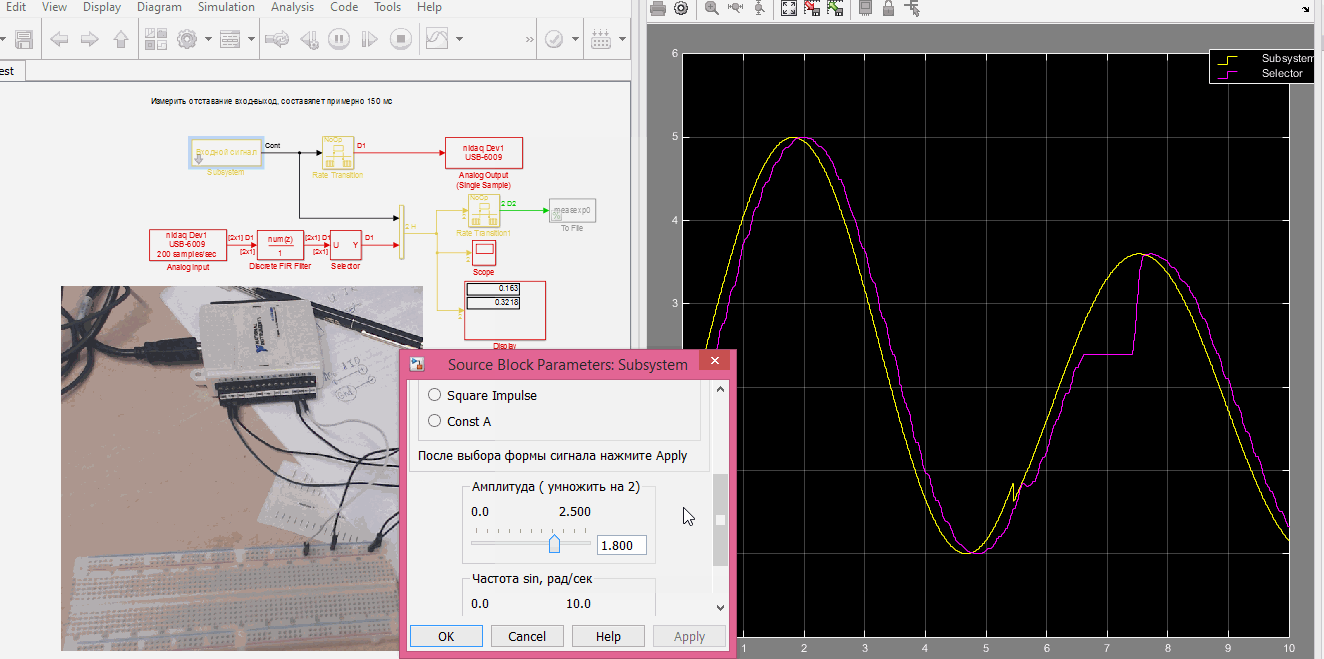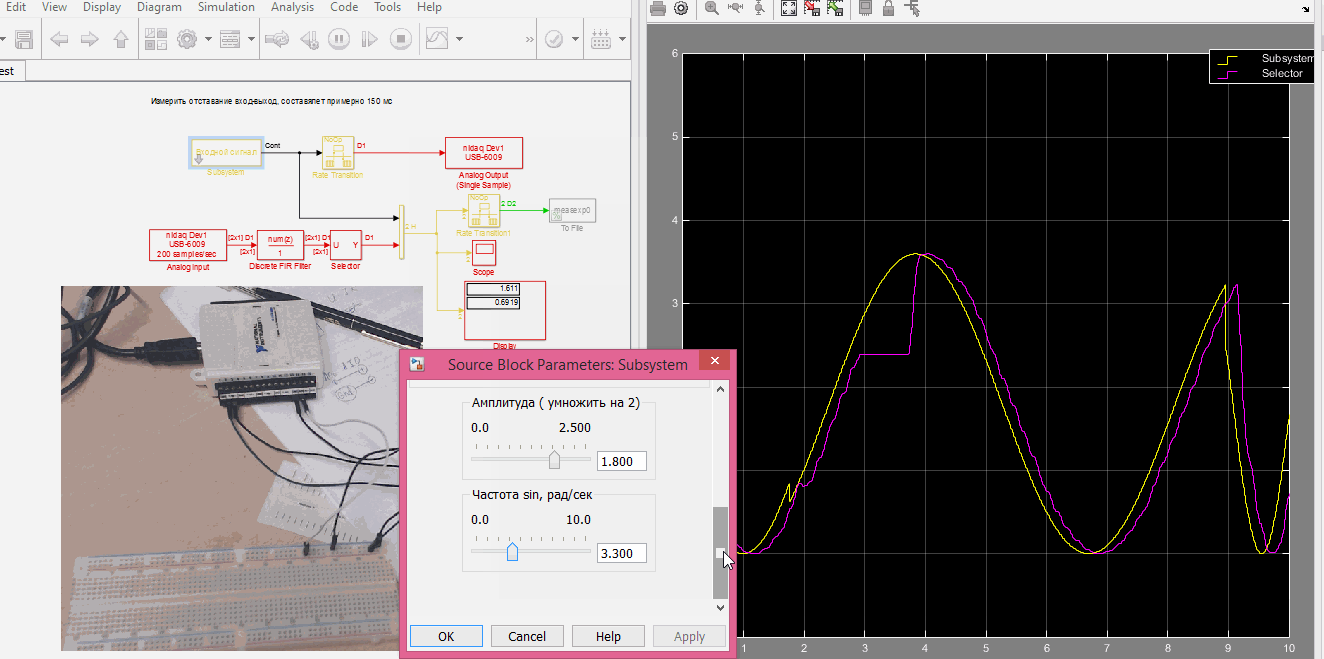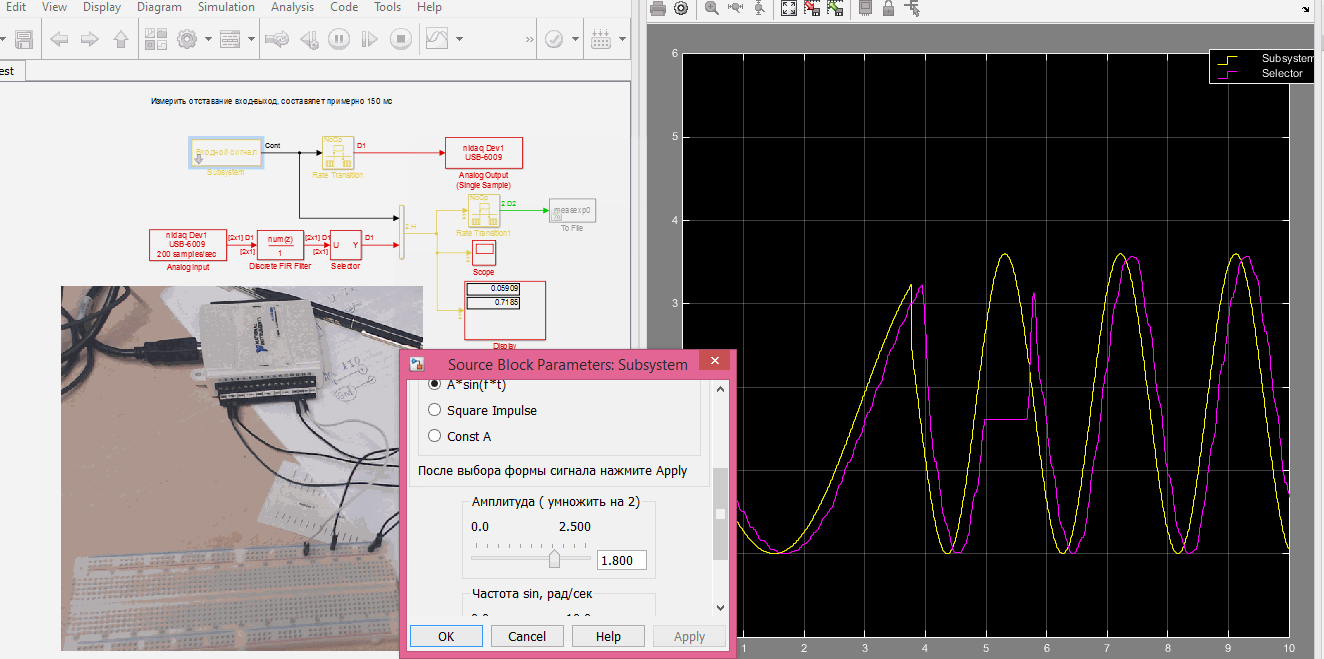
open SelfTest
Схема измерения
Схема может выглядеть следующим образом.

Аналоговый выход NI USB 6009 ограничен 5 В. В эксперименте использовался внешний источник напряжения - 7 В. Поэтому реальная схема не содержала аналогового выхода с устройства.
Загружаем данные эксперимента и обрезаем их
Интересует качественное сравнение, поэтому используем курсор мыши для выделения области измерений. Используем тип данных TimeSeries
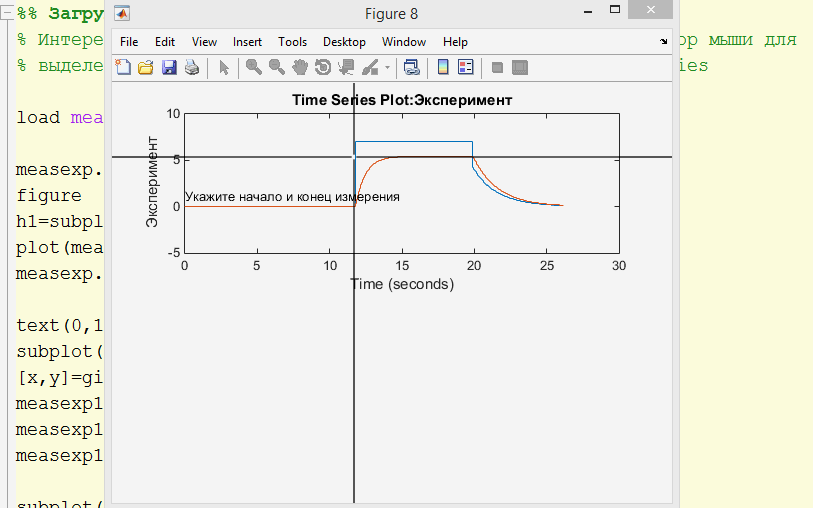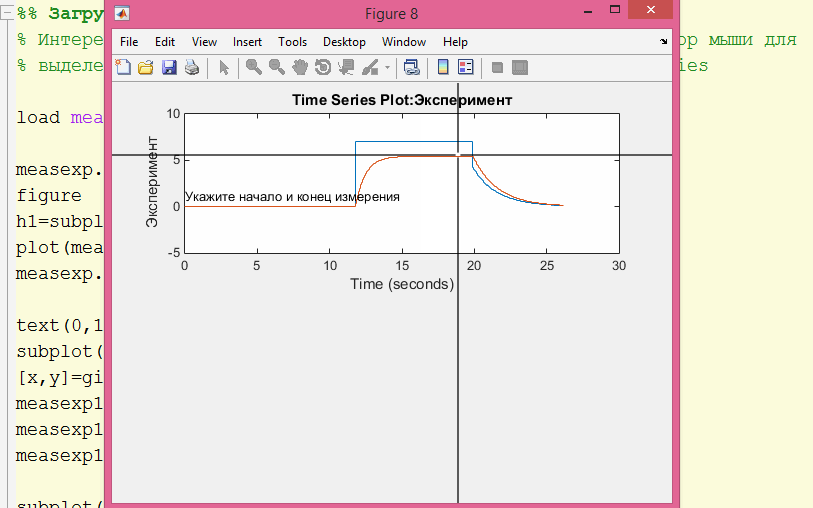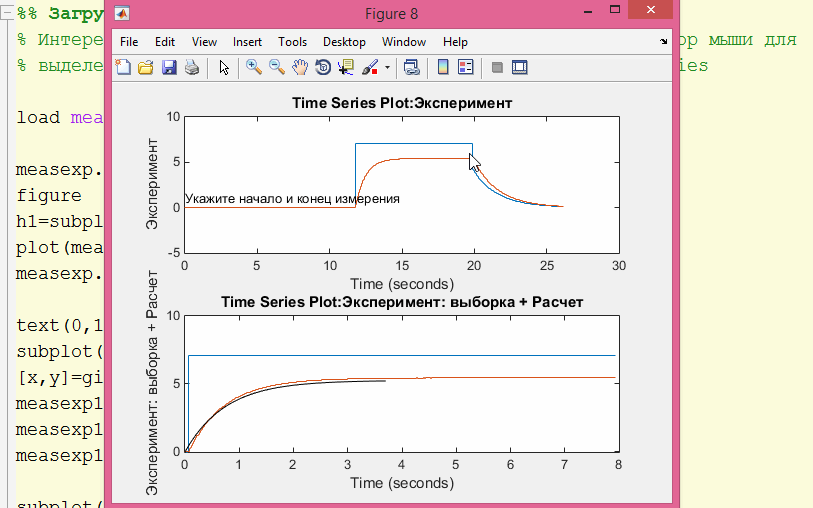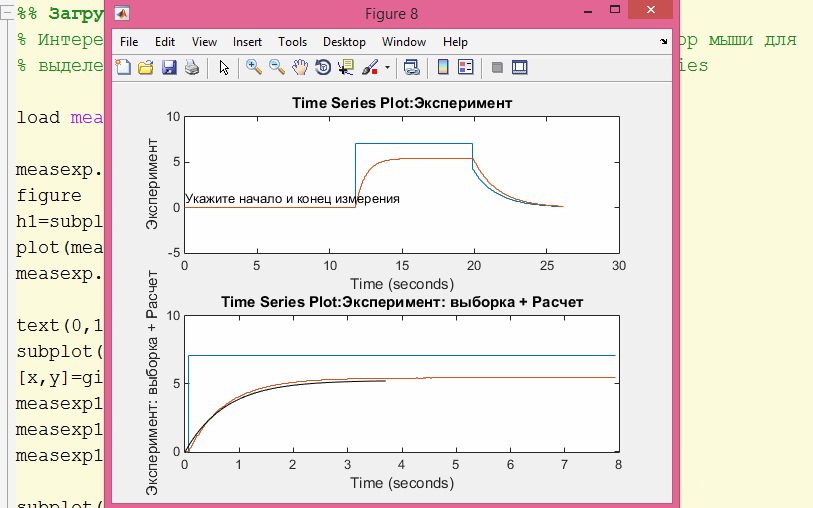
load measexp1 measexp.Name='Эксперимент' figure h1=subplot(2,1,1); plot(measexp) measexp.TimeInfo; text(0,1,'Укажите начало и конец измерения') subplot(h1); [x,y]=ginput(2); measexp1s = getsampleusingtime(measexp,x(1),x(2)); measexp1s.Time=measexp1s.Time-measexp1s.Time(1); measexp1s.Name='Эксперимент: выборка + Расчет'; subplot(2,1,2) measexp1s.plot hold on plot(ta,vc,'-k') hold off
Warning: The IsTimeFirst property is now calculated and differs from the saved
representation.
timeseries
Common Properties:
Name: 'Эксперимент'
Time: [1309x1 double]
TimeInfo: tsdata.timemetadata
Data: [1309x2 double]
DataInfo: tsdata.datametadata
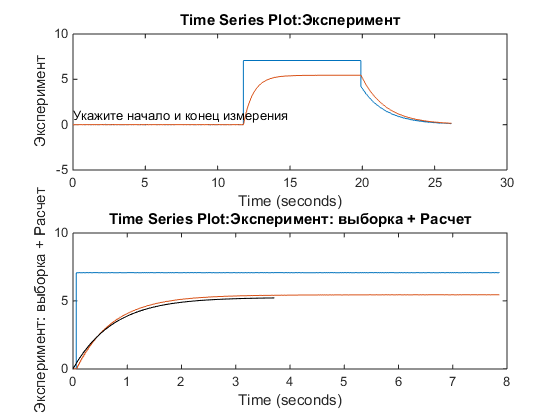
Подготавливаем данные для System Identification и Parameter Estimation
ymeas=squeeze(measexp1s.Data(:,2));
umeas=squeeze(measexp1s.Data(:,1));
time=measexp1s.Time;
% Используем специальный контейнер System Identification
exp1=iddata(ymeas,umeas,measexp.TimeInfo.Increment)
figure
plot(exp1)
VsE=max(umeas);
exp1 =
Time domain data set with 394 samples.
Sample time: 0.02 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1

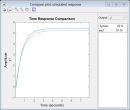
Сравниваем аналитическое решение и экспериментальное
uca=iddata(Vc(time),Vs*ones(size(umeas)),measexp.TimeInfo.Increment); compare(uca,exp1)
Системная идентификация
В качестве модели предполагаем y=Kp/(Tp1*s+1)*exp(-Td*s)
opt = procestOptions('OutputOffset', V0); exp1m=procest(exp1,'p1d',opt) % Сравниваем экспериментальные данные с моделью % Сравниваем аналитически полученные параметры и на основе идеентификации
exp1m =
Process model with transfer function:
Kp
G(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 0.76937
Tp1 = 0.68361
Td = 0
Parameterization:
'P1D'
Number of free coefficients: 3
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on time domain data "exp1".
Fit to estimation data: 99.17%
FPE: 0.0002176, MSE: 8.614e-05
Убираем постоянную составляющую
Это может быть полезно при наличии смещения, тогда получаемая модель оказывается точнее. Если смещения нет, то может быть хуже.
[data_d,T] = detrend(exp1,0); plot(data_d) % Получаем модель на данных без смещения exp1md=procest(data_d,'p1d'); % Моделируем и добавляем постоянную составляющую [y_sim]=sim(exp1md,data_d); y_sim = retrend(y_sim,T);
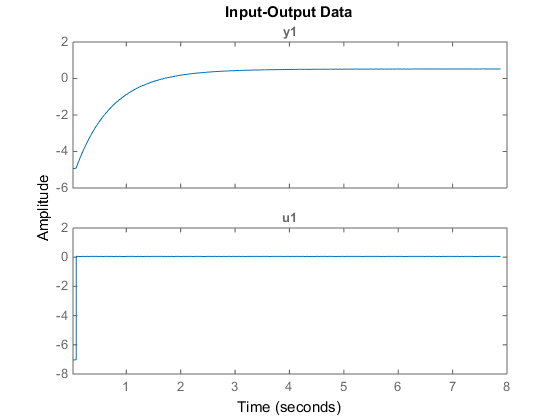
Сравниваем аналитически полученные параметры и на основе идентификации
На графике представлено сравнение полученной модели, аналитической модели и графика. Хуже всего результат у модели с вычетом тренда.
compare(exp1,y_sim,exp1m,uca) disp('Параметры') disp('Обычная модель Без тренда Аналитическая') disp([exp1m.Tp1 exp1md.Tp1 tau]) disp([exp1m.Kp exp1md.Kp K])
Параметры
Обычная модель Без тренда Аналитическая
0.6836 0.6912 0.7423
0.7694 8.4973 0.7423
Оптимизация модели
Подбирая параметры модели, добавляя элементы, можно добиться схожести результатов. Необходимо помнить, что модель изначально дана в идеальном виде и не учитывает многие параметры (например ток утечки).
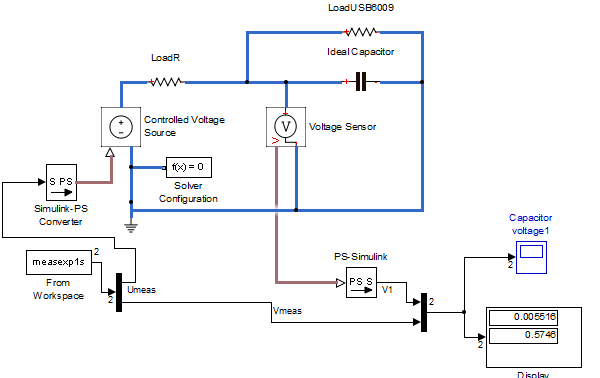
Parameter Estimation
Можно использовать автоматический подбор параметров, для этого подготовим модель, запустим Parameter Estimation.
Выбираем параметры для оценки
Выбираем параметры для оценки, указываем диапазон. В примере испортим значение сопротивления R2, которое ранее было измерено мультиметром. Его значение составляет примерно 288 кОм
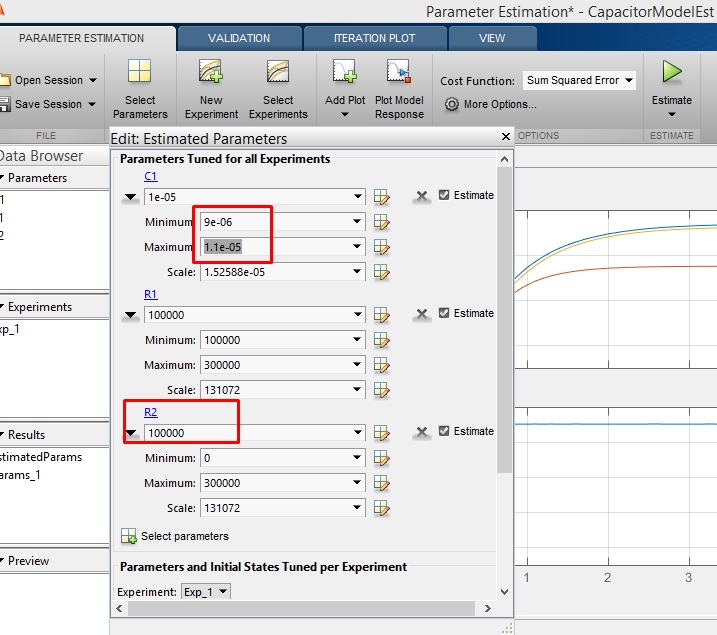
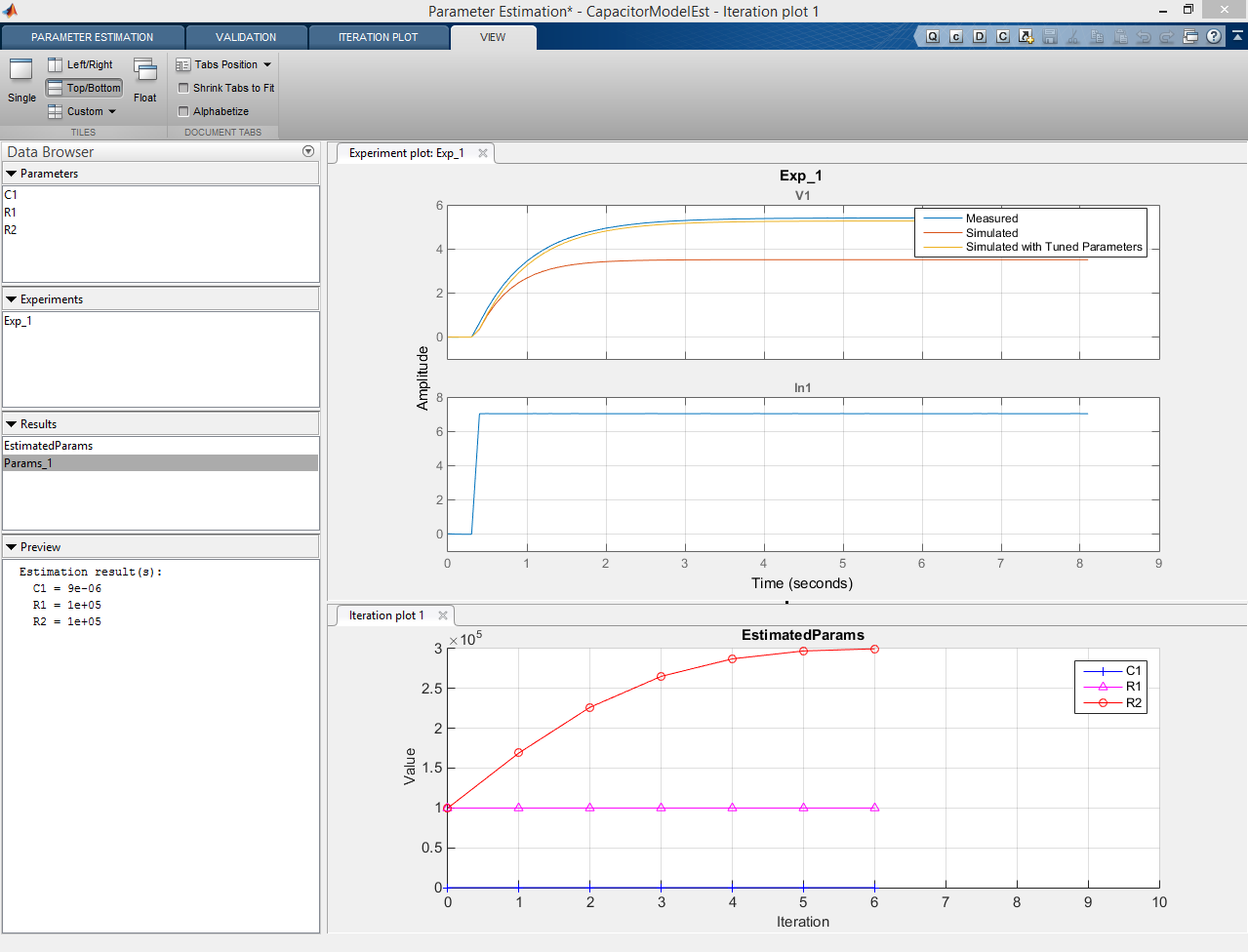
Результат подгонки параметров
В результате подгонки получили близкое значение. Результат симуляции также приближается к измеренным значениям.
Что дальше?
- Можно убрать из поиска известные параметры, сузить область поиска, точнее подогнать модель.
- Можно снять больше экспериментов, что бы провести валидацию полученной модели. При этом стоит подавать сигналы разной формы, амплитуды и длительности.
Выводы
- Вместе с Data Acquisition ToolBox и USB 6009 можно проводить эксперименты для подачи тестовых данных и съема сигналов
- System Identification позволяет проводить идентификацию динамических звеньев, но нужно помнить про обработку данных. Например, что бы убрать смещение или тренд, сделать фильтрацию, изменить шаг дискретизации данных
- Модель в Simulink + Simscape позволяет наглядно представить систему, понять как она может себя повести на базе симуляции
- При помощи Response Estimation мы можем попробовать восстановить значения параметров
Похожий пример в справочном руководстве
Используется Parameter estimation http://www.mathworks.com/help/sldo/examples/importing-and-preprocessing-experiment-data-gui.html
Использованные материалы
- MATHWORKS
- USER GUIDE AND SPECIFICATIONS NI USB-6008/6009
- Acquisition Card NI USB-6009 in Automatic Control Laboratory Exercises
Комментарии
Интересно, спасибо автору.