Исследование с помощью MATLAB компенсации систематической ошибки c помощью фильтра Калмана в информационно-измерительных системах

Автор - В.М. Понятский, Тульский государственный университет.

Рассматривается возможность оценивания состояния процесса на основе данных измерений нескольких датчиков при наличии систематической ошибки измерений, не поддающейся предварительной оценке и учету. Проводится анализ существующих подходов к комплексированию информации, использующих фильтрацию Калмана. Предложено проводить оценивание состояния процесса с раздельной коррекцией по показаниям отдельных датчиков. Компенсация систематической ошибки реализуется в процедуре предсказания, используя измерения с систематической ошибкой в качестве внешнего управляющего сигнала.

1. Введение

В современных информационно-измерительных системах, использующих несколько датчиков для получения информации о параметрах объекта или процесса, центральным является вопрос выбора способа объединения полученных данных. Традиционно применяемым алгоритмом оценивания параметров процесса на основе зашумленных данных измерений является фильтр Калмана, позволяющий получить несмещенную оценку с минимальной дисперсией при условии априорного знания характеристик шумов, присущих измерителю и самому процессу. Однако в ряде случаев в показаниях датчиков могут присутствовать помимо шумов систематические ошибки измерений, величина которых зачастую не может быть оценена и учтена заранее. В [1, 2] предложено в этом случае, измерения с систематической ошибкой использовать в процедуре предсказания фильтра Калмана в качестве внешнего воздействия.

Известно несколько подходов к объединению показаний с различных измерителей. Согласно одному из них [3], для каждого из измерителей используется отдельный фильтр, вырабатывающий свои оценки вектора состояния и ковариационной матрицы. Получается итоговая оценка, оптимальная в смысле минимизации ее дисперсии, с учетом коррелированности оценок каждого фильтра. Этот подход получил устоявшееся название «объединение векторов состояния» (state vector fusion).

Другой подход предполагает использование одного фильтра Калмана независимо от числа измерителей и представляет собой «объединение измерений» (measurement fusion). При этом объединение показаний выполняется до начала процесса фильтрации и может сопровождаться комплексированием по критерию минимума среднеквадратической ошибки, как в [4].

В [5] предлагается выполнять оценки состояния процесса раздельно по показаниям отдельных датчиков с формированием множества векторов состояния, а предсказание выполнять по объединенной оценке вектора.

Последний подход позволяет проводить введение измерения с систематической ошибкой как внешнего управляющего воздействия и может быть использован при компенсации систематической ошибки в показаниях.

В настоящей работе рассматривается возможность компенсации систематической ошибки при комплексировании измерений, базирующейся на раздельной коррекции вектора состояния процесса по показаниям отдельных измерителей и использованием измерений с систематической ошибкой как внешнего управляющего воздействия.

 

2. Учет систематической ошибки

при объединении информации с датчиков

Дискретный алгоритм оценивания состояния объекта управления в рамках методов фильтрации Калмана имеет вид [6]:

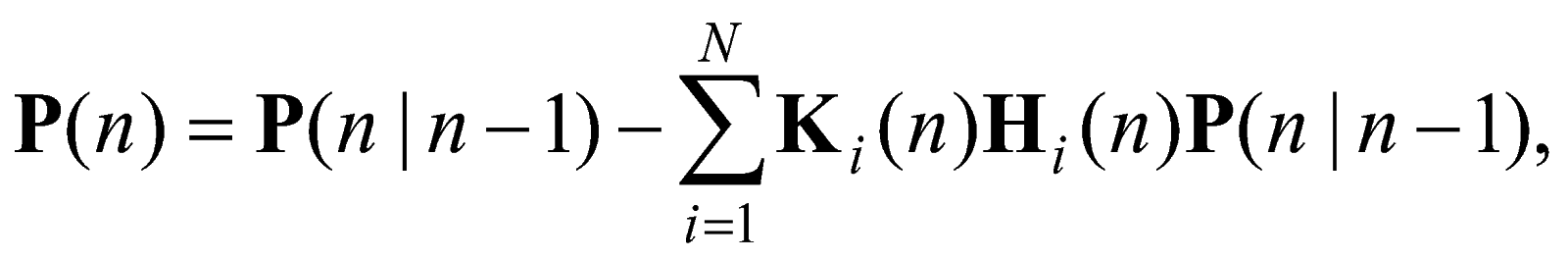
где – вектор наблюдений; – вектор оценок наблюдений; – оценка вектора состояния наблюдаемого объекта или процесса; – оценка скорректированного вектора состояния наблюдаемого объекта или процесса; – оценка вектора прогнозирования состояния наблюдаемого объекта или процесса; – матрица упреждения; – матрица наблюдения; – матрица коэффициентов; – дисперсионная матрица предсказания вектора состояния наблюдаемого объекта или процесса; – дисперсионная матрица оценки вектора состояния наблюдаемого объекта или процесса; – матрица интенсивности шумов; – матрица интенсивности полезного сигнала; – вектор управления; – матрица коэффициентов управления; – вектор весовых коэффициентов; – процедура коррекции оценок фильтра Калмана, – признак типа измерителя или отсутствия измерений ; – количество измерителей.

На рис. 1 показана схема комплексирования сигналов N измерителей, включающая процедуры предсказания, объединения и коррекции, позволяющие получить на выходе оценку состояния процесса при наличии систематической ошибки в измерениях.

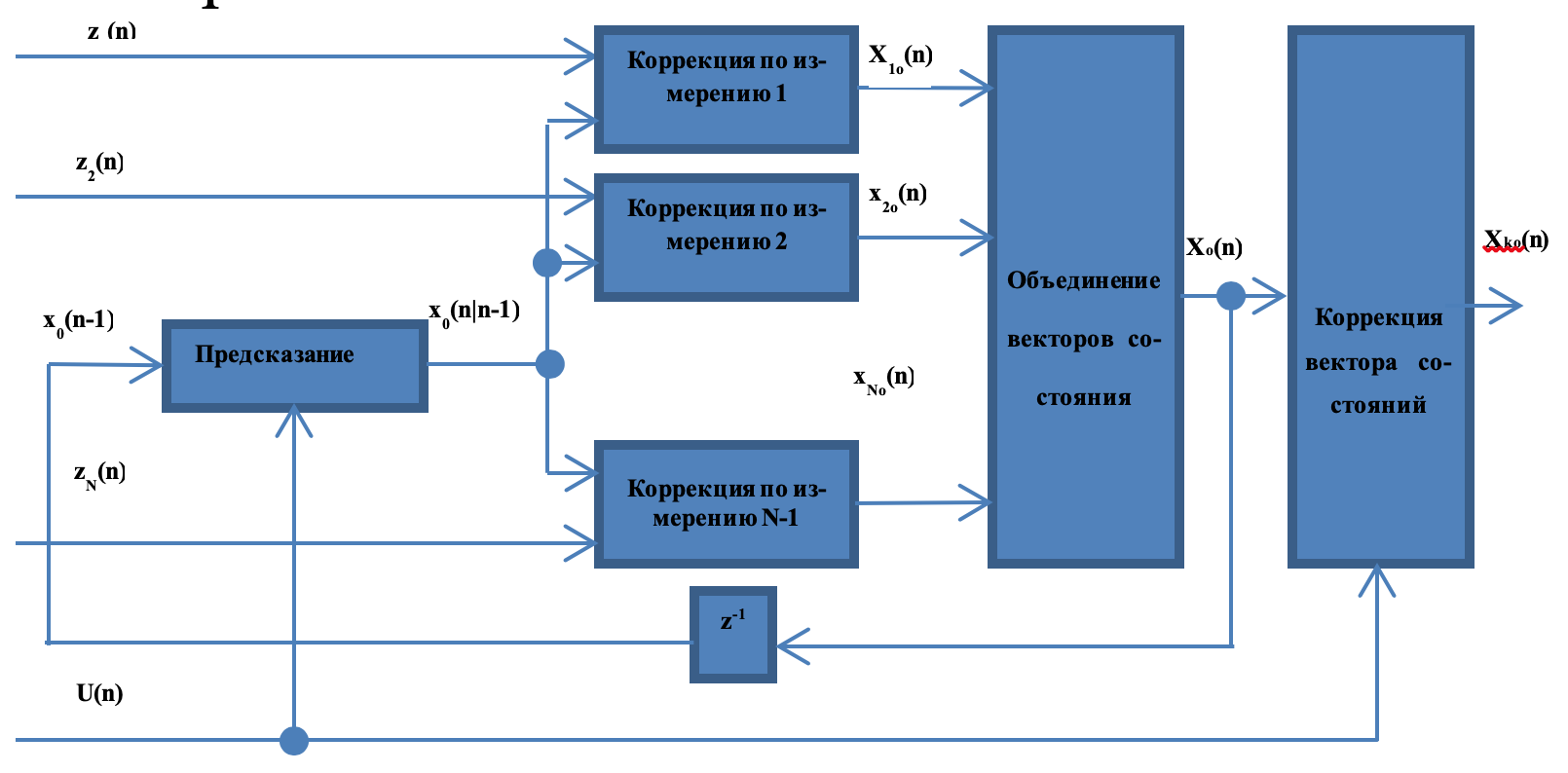
Рис. 1. Схема фильтра Калмана с компенсацией систематической ошибки измерений

Непрерывный алгоритм фильтрации Калмана имеет вид [7]:

(1)

где – вектор измерений i-го датчика; – вектор оценок наблюдений; – оценка скорректированного вектора состояния наблюдаемого процесса;– оценка вектора состояния наблюдаемого процесса; – матрица упреждения; – корреляционная матрица ошибок фильтрации; – матрица наблюдения; – вектор коэффициентов усиления; – матрица интенсивности шумов; – матрица интенсивности полезного сигнала; – вектор управления; – матрица коэффициентов управления; – матрица весовых коэффициентов; – процедура коррекции оценки фильтра Калмана, – признак типа и качества измерений или отсутствия измерений , - количество измерителей.

 

3. Результаты исследования

Рассмотрим систему, в которой совокупность датчиков служит для определения ориентации твердого тела, состоящая из датчиков угловых скоростей и акселерометров. Первые выдают достаточно точные показания на коротких промежутках времени, но обладают долгосрочной нестабильностью, выражающейся в появлении низкочастотного дрейфа, вызывающего со временем накопление ошибки. Акселерометры, напротив, выдают несмещенные, но сильно зашумленные в высокочастотной области показания. Выработка оценки состояния объекта на выходе фильтра возможна в рамках двух различных подходов [7]. Первый подход заключается в организации двухканального фильтра, предполагающего коррекцию оценки параметров процесса с помощью взвешенной суммы двух инноваций, соответствующих каждая одному из имеющихся типов датчиков:

(2)

Второй подход базируется на использовании данных датчика с систематической ошибкой при предсказании, т.е. в качестве вектора внешнего воздействия (управления) , влияющего на оценку состояния процесса, и последующей корректировке ее с помощью измерений, полученных с другого датчика (одноканальный фильтр):

(3)

Сравнительный анализ описанных подходов проводится в среде Matlab на примере оценки регулярного гармонического воздействия на систему, содержащую два измерителя. Сравнительный анализ описанных подходов проводится на примере оценки регулярного гармонического воздействия системой двух измерителей, позволяющих получать показания по одной угловой координате , , но может быть распространен на случай трехосевых измерений без потери общности. Реализации фильтров на основе уравнений (2) и (3) представлены на рис. 2 и 3 соответственно. Оценка вектора состояния производится с помощью фильтрующих звеньев второго порядка. Для двухканального фильтра соответствующие матрицы выглядят следующим образом (рис. 2):

, , , , .

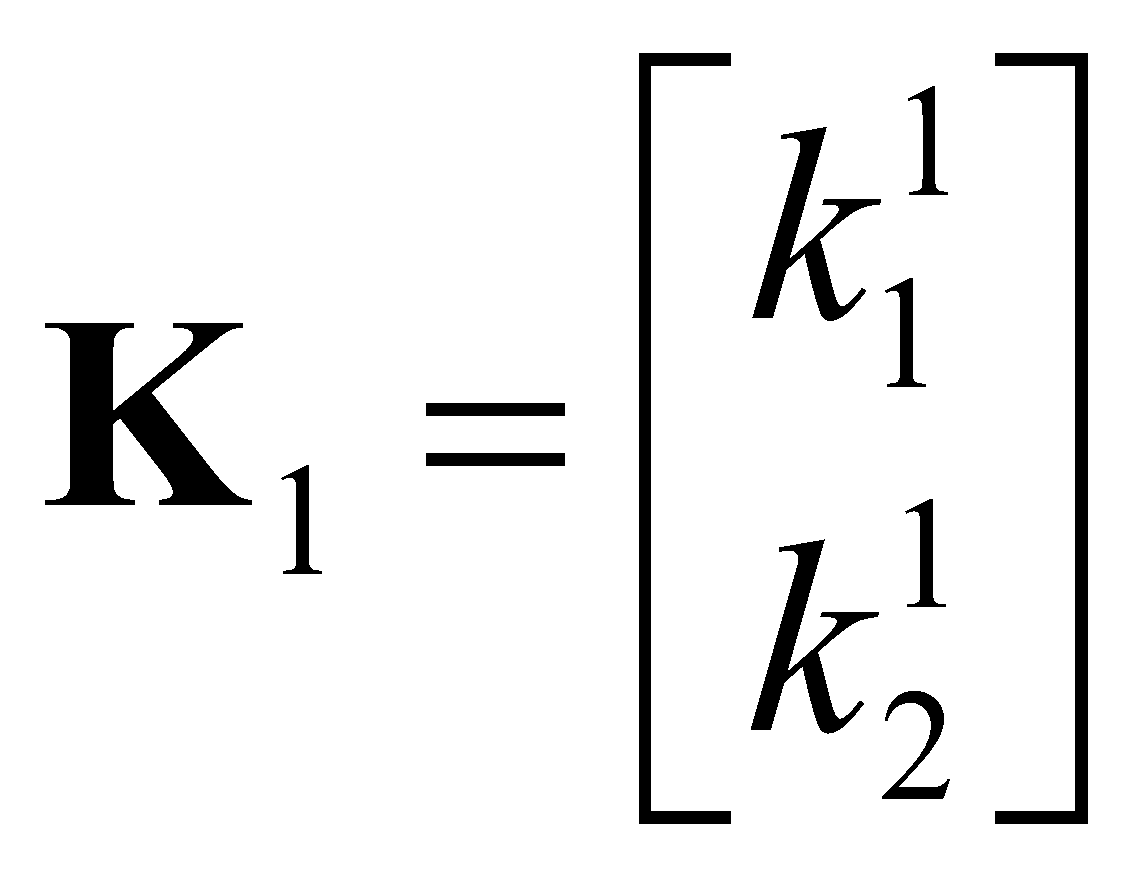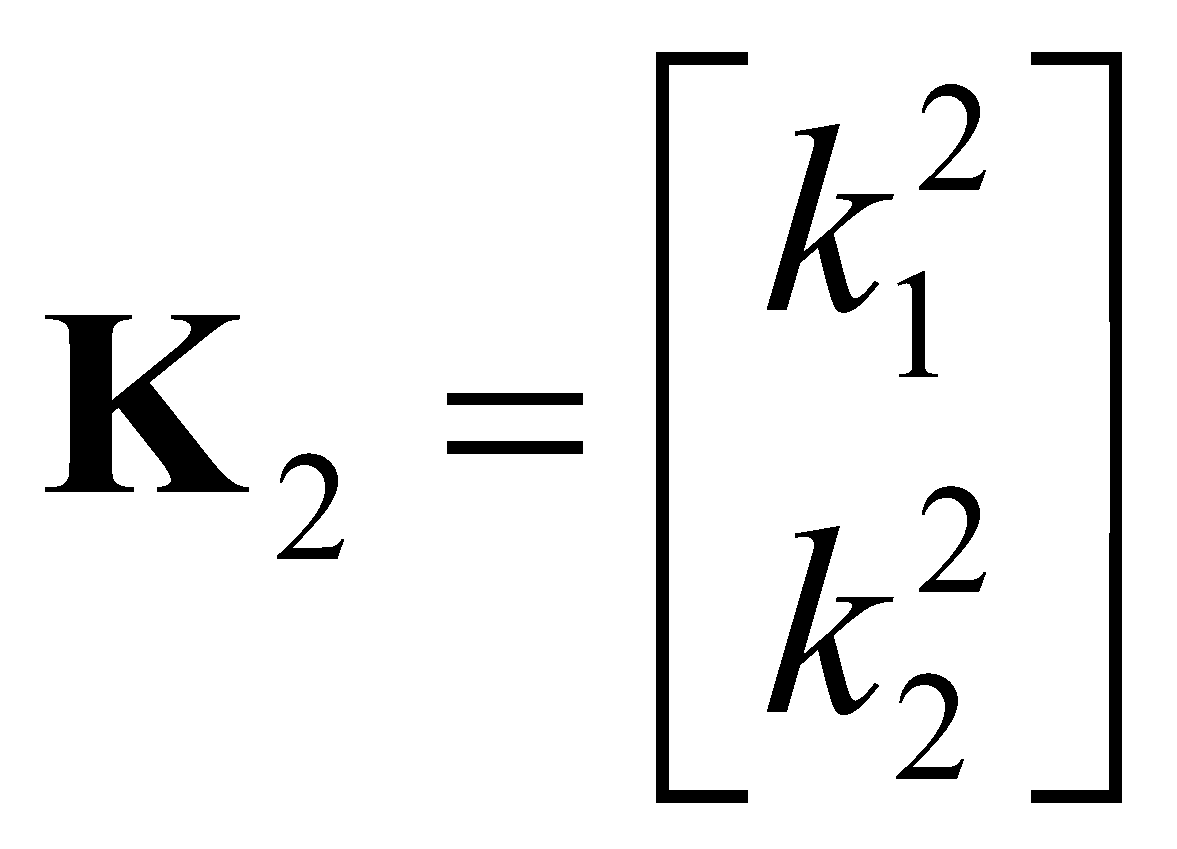Для одноканального фильтра при учете измерений угловой скорости в виде управляющего воздействия (рис. 3):

, , , .

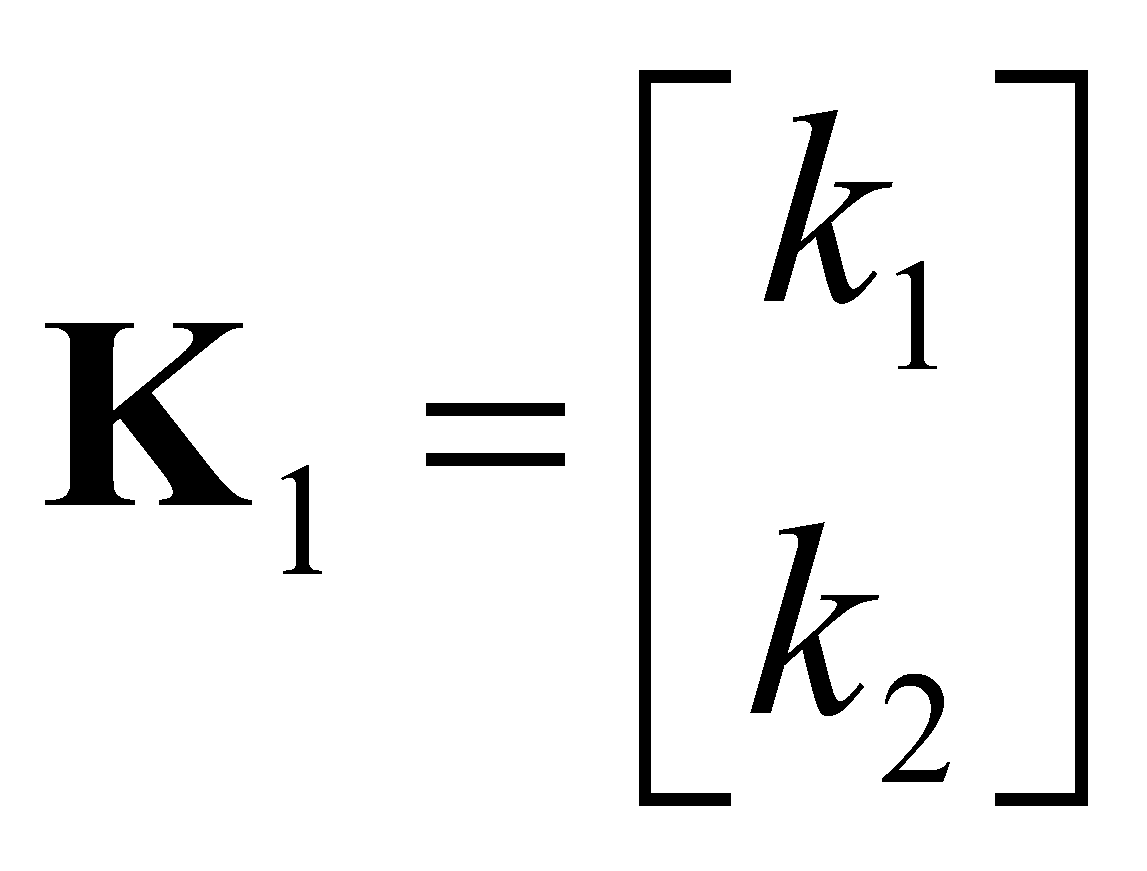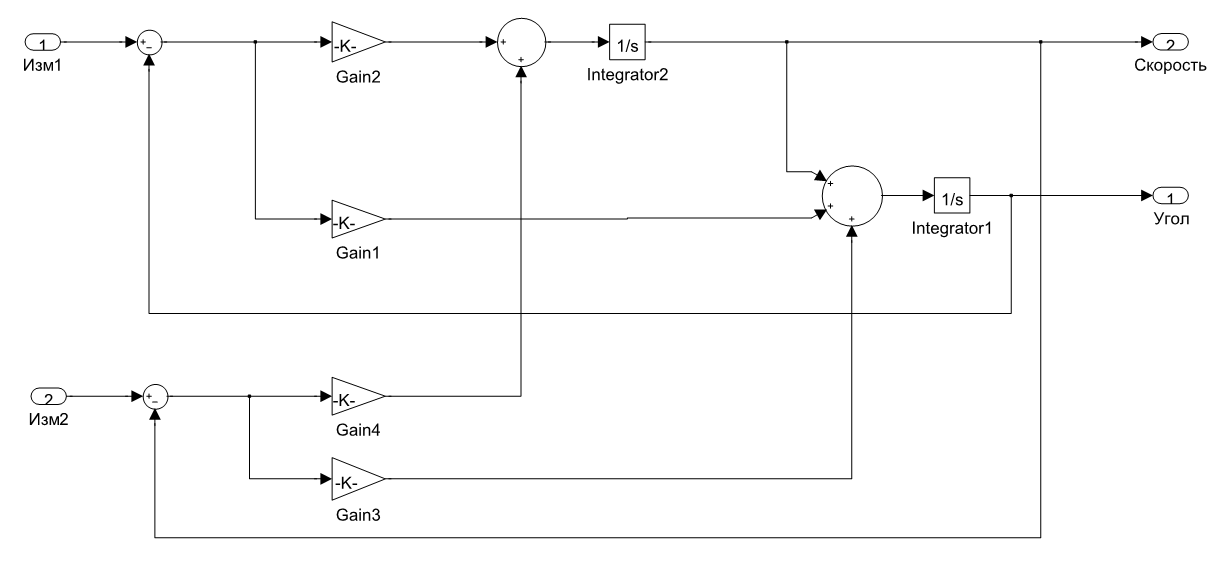
Рис. 2. Схема фильтра оценки угловой ориентации тела с двухканальной фильтрацией результатов измерения

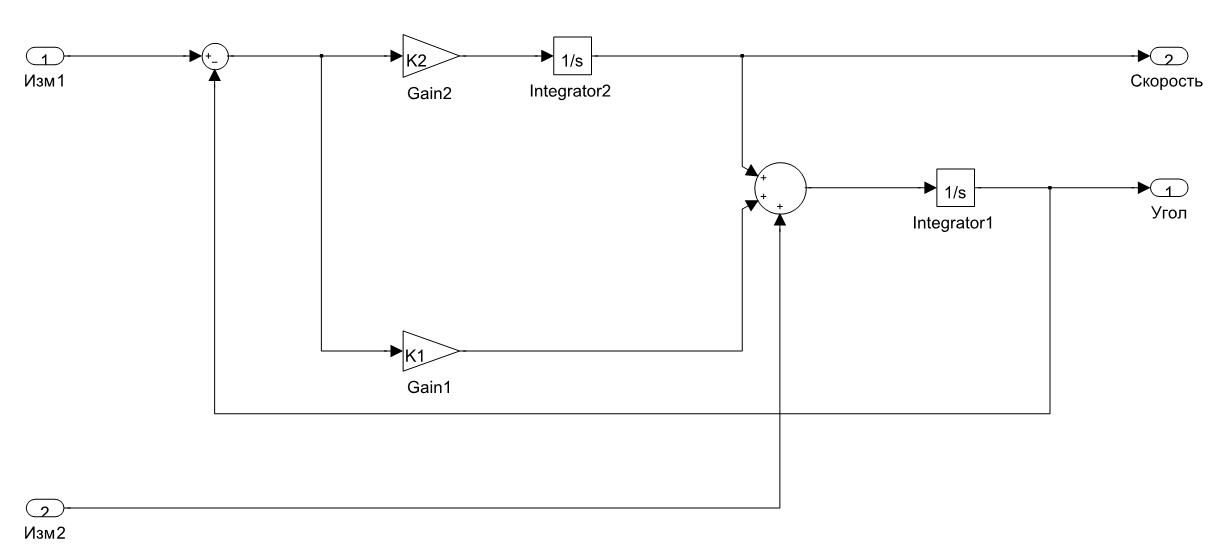
Рис. 3. Схема фильтра оценки угловой ориентации тела с одноканальной фильтрацией результатов измерения и управляющим входом

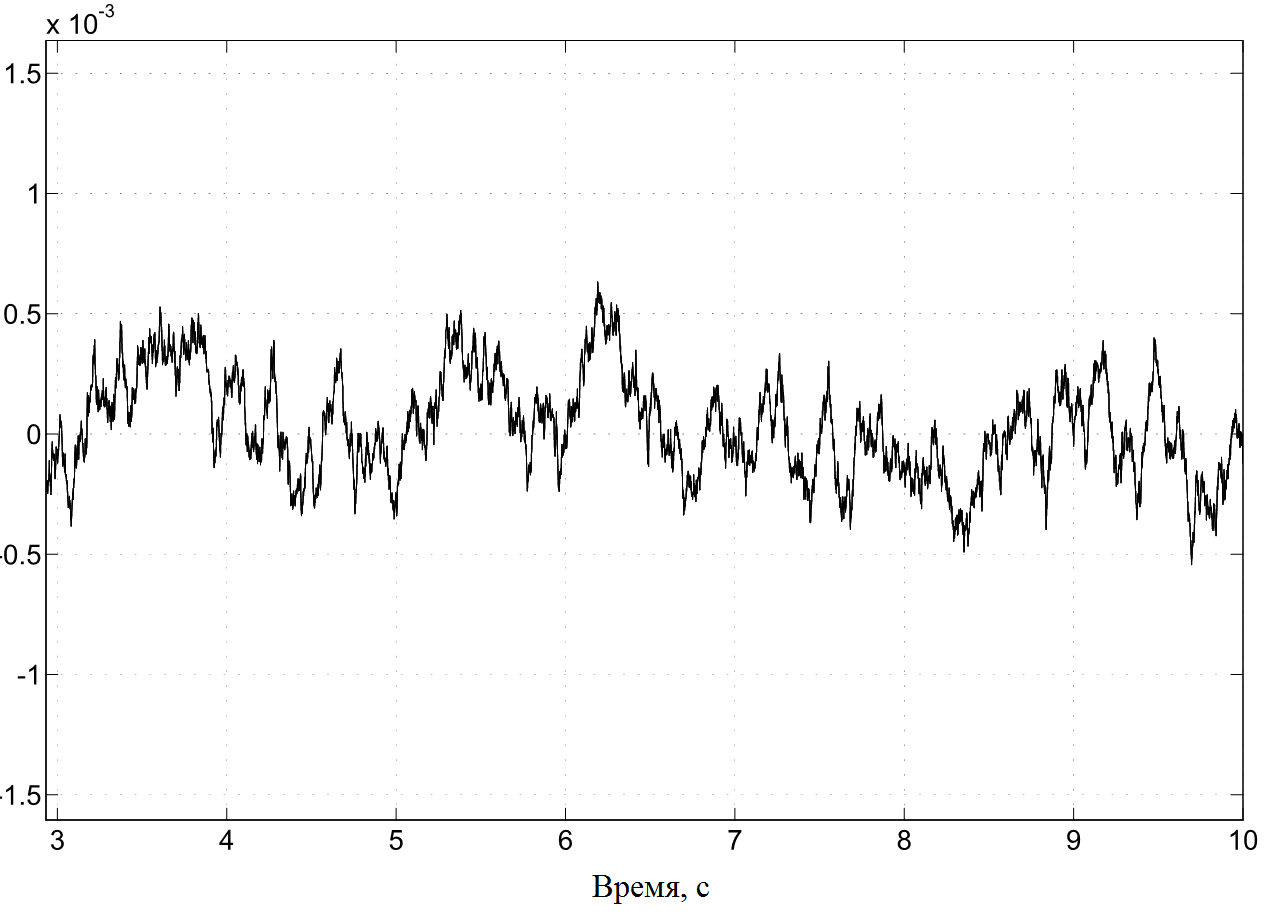
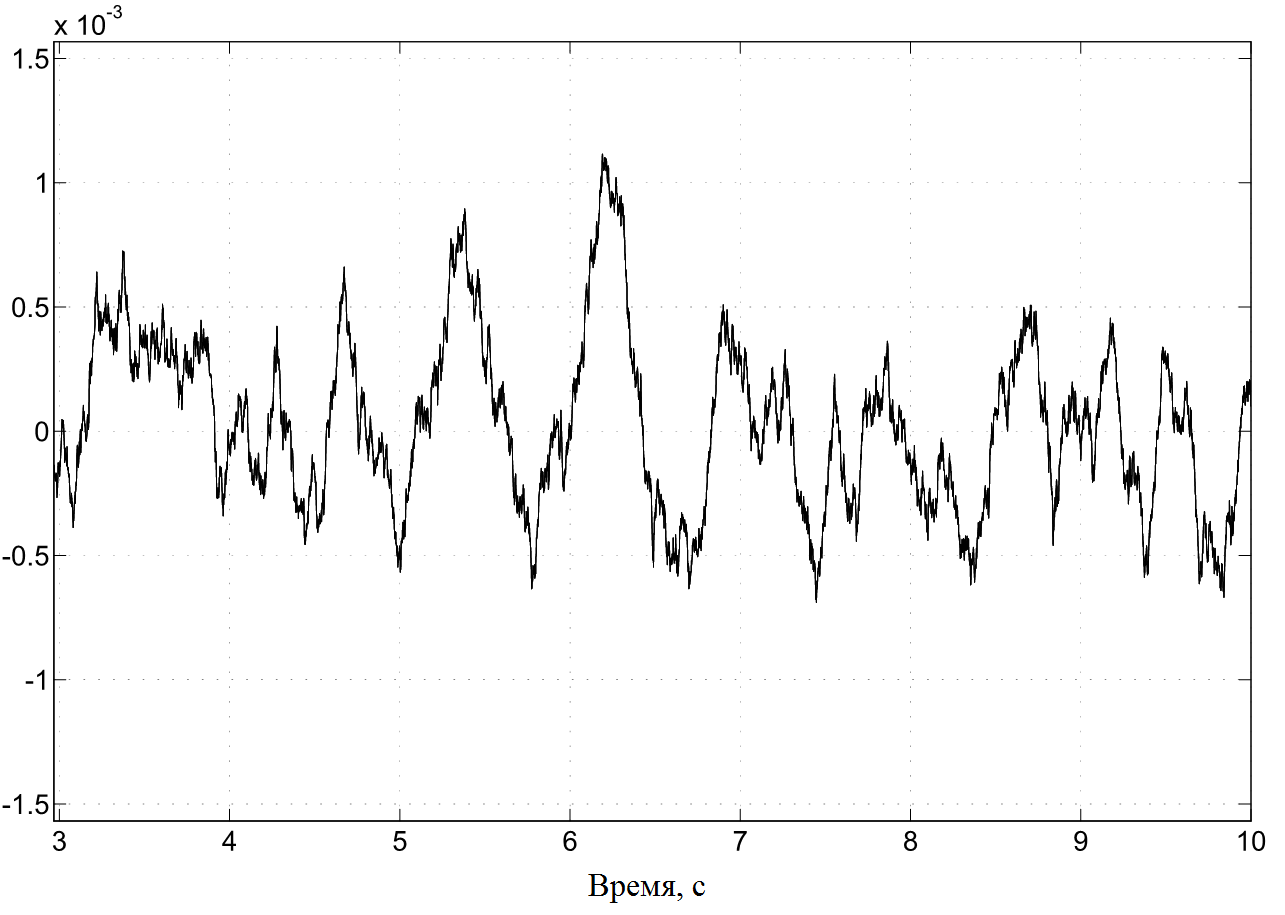
Результаты работы фильтров при небольших амплитудах шумов измерений представлены на рис. 4а – 4б. Как видно из графиков, двухканальный вариант фильтра имеет в установившемся режиме большую ошибку оценивания, чем одноканальный.

а

б

в

г

Рис. 4. Ошибки оценки угла на выходе: а, в - двухканального фильтра; б, г - одноканального фильтра

В случае присутствия в системе сильношумящих датчиков использование двухканального варианта фильтрации становится более предпочтительным, что хорошо иллюстрируется рис. 4в – 4г.

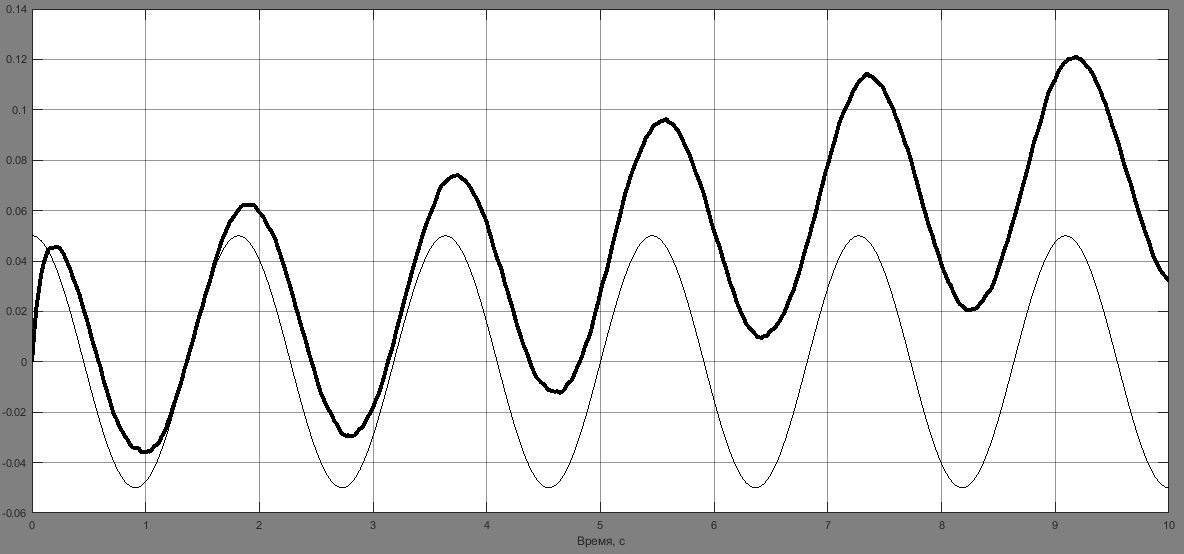
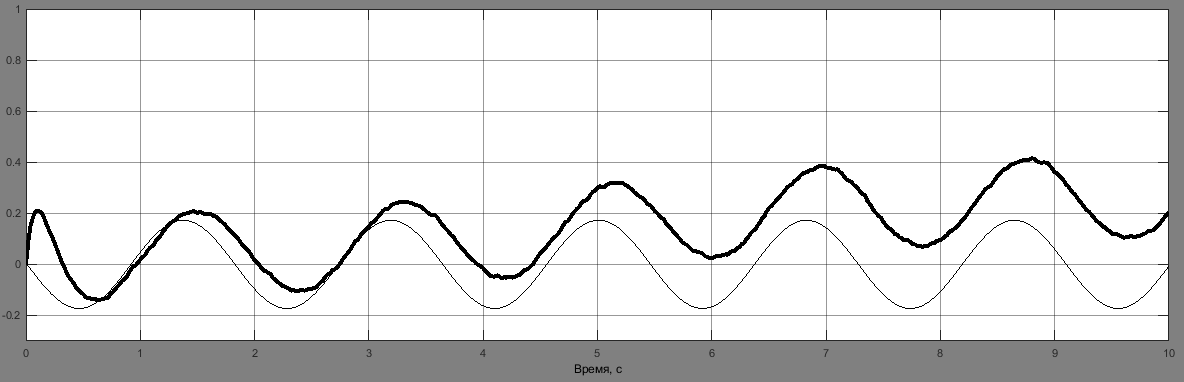
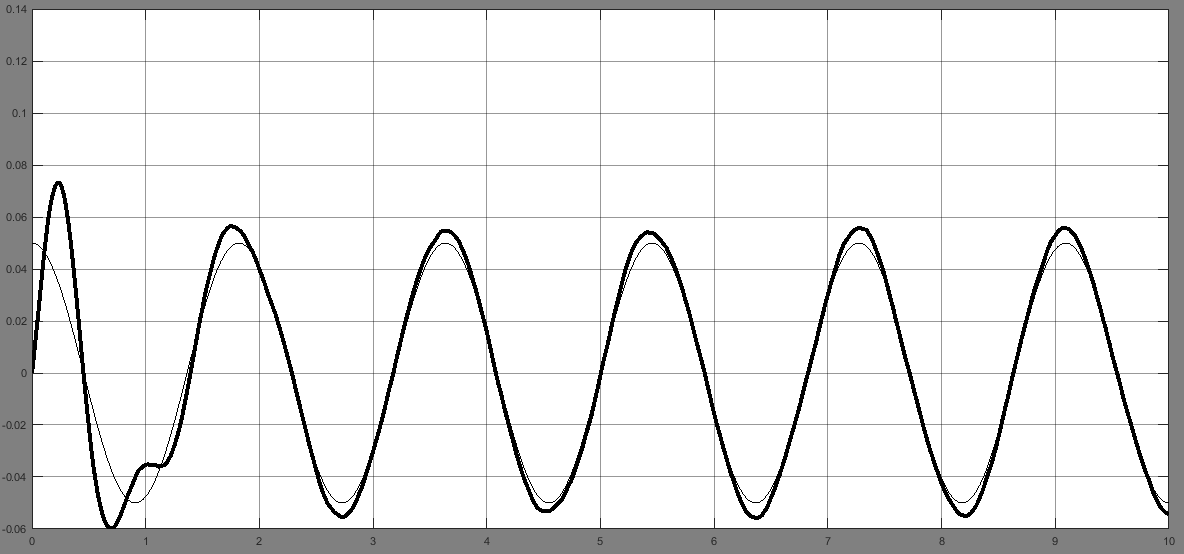
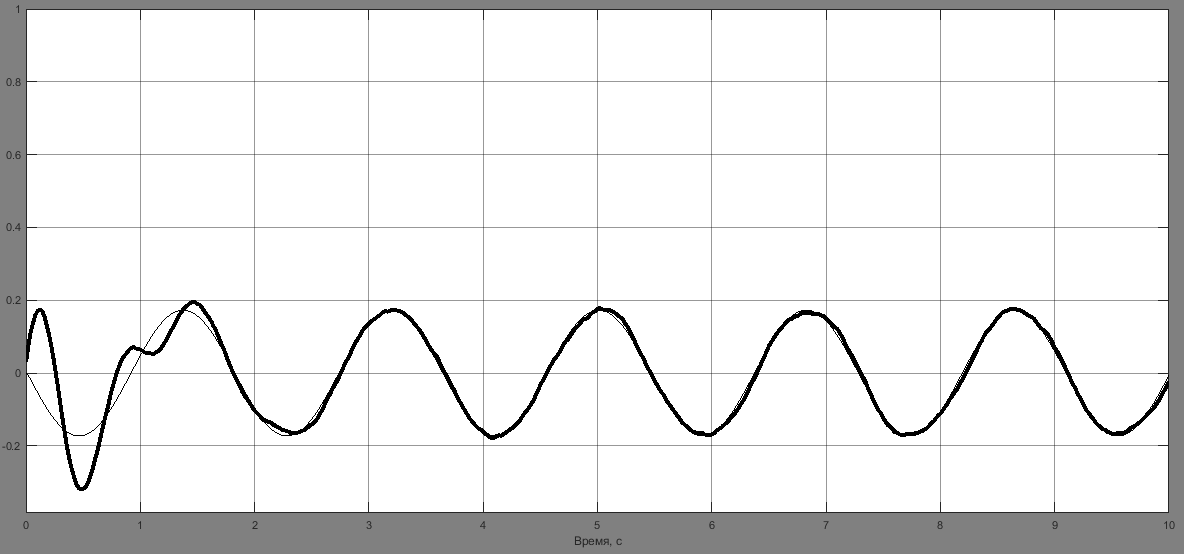
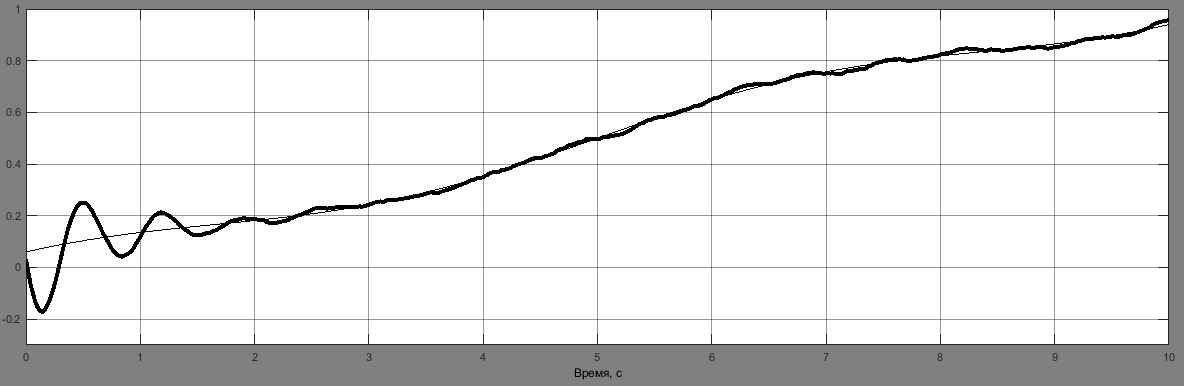
При появлении в данных одного из измерителей систематической ошибки одноканальный вариант фильтрации показывает лучшие результаты по сравнению с двухканальным фильтром. На рис. 5 приведены оценки угла, угловой скорости и систематической ошибки измерений на выходе двухканального и одноканального фильтра.

а	б
в	г		д

Рис. 5. Результаты оценки: а – угла на выходе двухканального фильтра; б – угловой скорости на выходе двухканального фильтра; в – угла на выходе одноканального фильтра; г – угловой скорости на выходе одноканального фильтра; д – систематической ошибки измерений на выходе одноканального фильтра

Результаты показывают, что в одноканальном фильтре систематическая ошибка после окончания переходного процесса выделяется с достаточной степенью точности, что позволяет использовать ее для коррекции вектора состояний.

 

4. Заключение

Таким образом, получение несмещенной оценки состояния процесса на основе данных измерений возможно при раздельной коррекции вектора состояния по данным датчиков и введения в процедуру предсказания через внешнее воздействие результатов измерений содержащих систематическую ошибку.

 

Список литературы

1. http://blog.tkjelectronics.dk/2012/09/a-practical-approach-to-kalman-filter-and-how-to-implement-it.

2. Шпекторов А.Г., Фам В.Т. Анализ применения микромеханических измерительных систем для задач управления морскими подвижными объектами // Известия СПбГЭТУ «ЛЭТИ». 2017. №5. С. 16-20.

3. Bar-Shalom Y., Campo L. The effect of the common process noise on the two-sensor fused-track covariance // IEEE Transactions on Aerospace and Electronic Systems. 1986. Vol. 22. No. 11. P. 803-805.

4. Roecker J.A., McGillem C.D. Comparison of two-sensor tracking methods based on state vector fusion and measurement fusion // IEEE Transactions on Aerospace and Electronic Systems. 1988. Vol. 24. No. 4. P. 447-449.

5. Gao J.B., Harris C.J. Some remarks on Kalman Filters for the multisensory fusion // Information Fusion. 2002. No. 3. P. 191-201.

6. Понятский В.М. Повышение качества обработки информации, поступающей с нескольких видеосенсоров, в задачах управления // Современные информационные технологии и ИТ-образование. 2016. Т. 12. № 4. С. 165–172.

7. Понятский В.М., Зенов Б.В. Применение фильтра Калмана для задач управления подвижными объектами // Современные информационные технологии и ИТ-образование. 2018. Т. 14. № 3. С. 625-630.