Список функций SNAE Toolbox
В этом разделе описаны функции, составляющие основу пакета SNAE и реализованные в виде M-файлов. Имена файлов совпадают с именами соответствующих функций. Каждый файл содержит комментарии с указанием назначения и правил обращения к данной функции. Функции расположены в алфавитном порядке.
Список функций SNAE Toolbox: Оглавление
В этом разделе описаны функции, составляющие основу пакета SNAE и реализованные в виде M-файлов. Имена файлов совпадают с именами соответствующих функций. Каждый файл содержит комментарии с указанием назначения и правил обращения к данной функции. Функции расположены в алфавитном порядке.
-
basisx, basisy - определение структуры базиса
-
demosnae - решение СНАУ от двух переменных
-
dimm - вычисление характеристик матрицы Mt
-
formm - формирование и вывод на экран характеристик матриц Mt
-
ker - вычисление нуль-пространства СНАУ
-
kroneck - вычисление характеристик структуры Кронекера
-
numb - вычисление номера столбца матрицы
-
pencil - вычисление матриц пучка
-
permut - вычисление строки перестановок
-
poleq - вычисление компонентов матрицы вспомогательной СНАУ
-
polsol - формирование вспомогательной СНАУ
-
pr_table - формирование таблицы RGSVD-разложения
-
pr_tablm - формирование таблицы характеристик матрицы Mt
-
reduc - редукция числа переменных СНАУ
-
rgsvd - вычисление RGSVD-разложения для пучка матриц
-
rmovcmpl - удаление из вектора комплексных элементов
-
rmovel - удаление совпадающих элементов вектора
-
rmovstr - удаление совпадающих строк матрицы
-
solsnae1 - решение СНАУ от одной переменной
-
solsnae2 - решение СНАУ от двух переменных
-
snae1 - решение СНАУ от одной переменной
-
snae2 - решение СНАУ от двух переменных
-
solssp, dsolssp - решение системы спектральных задач
-
ssnae2, dsnae2 - решение СНАУ от двух переменных
-
struct - вычисляет структуру Кронекера прямоугольного пучка
-
trunc - обработка и усечение вектора решений
-
wr3pos - подсчет количества цифр в числе
basisx, basisy - определение структуры базиса
Синтаксис:
XN = basisx(sx, sy)
YN = basisy(sx, sy)
Описание:
Функция XN = basisx(sx, sy) формирует представление базиса [x ![]() y] для СНАУ от двух переменных в виде строки символов.
y] для СНАУ от двух переменных в виде строки символов.
Входные переменные:
-
sx - максимальная степень переменной x;
-
sy - максимальная степень переменной y.
Выходные переменные:
-
XN - строка, характеризующая структуру базиса СНАУ.
Функция YN = basisx(sx, sy) формирует представление базиса [y ![]() x] для СНАУ от двух переменных в виде строки символов.
x] для СНАУ от двух переменных в виде строки символов.
Входные переменные:
-
sx - максимальная степень переменной x;
-
sy - максимальная степень переменной y.
Выходные переменные:
YN - строка, характеризующая структуру базиса СНАУ.
Пример:
| sx = 2; sy = 1; XN = basis(sx, sy) XN = [xxy xx xy x y] |
sx = 2; sy = 1 YN = basis(sx, sy) YN = [yxx yx y xx x 1] |
Используемые функции: нет.
demosnae - решение СНАУ от двух переменных
Синтаксис:
demosnae
Описание:
Демонстрационный Script-файл, предназначенный для решения систем нелинейных алгебраических уравнений от двух переменных.
% ********************************************************
% Решение
% систем нелинейных алгебраических уравнений (СНАУ)
% от двух переменных:
% Axy*[x**y] = 0,
% ********************************************************
% Axy - матрица размера p*N;
% N - число столбцов матрицы Axy;
% x, y - вектора алгебраической структуры
% sx jx
% [ x*..*x ... x*..*x ... 1 ],
% sy jy
% [ y*..*y ... y*..*y ... 1 ]
% jx, jy - степени переменных;
% sx, sy - максимальные степени переменных;
% x**y - произведение Кронекера.
dimm - вычисление характеристик матрицы Mt
Синтаксис:
[mt, Nt, Rt, mu, err] = dimm(a, b, t)
Описание:
Функция [mt, Nt, Rt, mu, err] = dimm(a, b, t) вычисляет размерности образа, ядра и число столбцов матрицы

размера m*(t+2) x n*(t+1), который не должен превышать при использовании версии системы MATLAB Student Edition 108 x 108 элементов.
Входные переменные:
-
a, b - матрицы пучка D(x)=a - x*b;
-
t - степень полиномиального решения.
Выходные переменные:
-
mt - число строк матрицы Mt;
-
Nt - число столбцов матрицы Mt;
-
Rt - размерность образа dim.Im(Mt) (ранг матрицы Mt);
-
mu - размерность ядра dim.Ker(Mt).
Используемые функции:
MATLAB: rank, eval, size, zeros.
Пакет СНАУ: нет.
formm - формирование и вывод на экран характеристик матриц Mt
Синтаксис:
[mutx, muvy] = formm(Dx, Dy, alrx, alry)
Описание:
Функция [mutx, muvy] = formm(Dx, Dy, alrx, alry) выводит на экран две таблицы характеристик матриц M(t & v), для Dx и Dy соответственно, вида:
s m n rnk mu alr
_____________________________
1 16 10 10 0 0
2 24 20 20 0 0
3 32 30 30 0 0
4 40 40 40 0 0
5 48 50 48 2 2
_____________________________
Входные переменные:
-
Dx, Dy - сингулярные пучки ax - x*bx, ay - y*by;
-
alrx, alry - информационные векторы структуры Кронекера для пучков Dx, Dy
Используемые функции:
MATLAB: нет.
Пакет СНАУ: dimm, pr_tablm.
ker - вычисление нуль-пространства СНАУ
Синтаксис:
q0 = ker(a, st, meps)
Описание:
Функция q0 = ker(a, st, meps) вычисляет нуль-пространство (ядро) q0=ker(a) прямоугольной матрицы на основе SVD- или QR-разложения; если ядро отсутствует, то q0=[ ].
Входные переменные:
-
а - матрица размера mа*nа (mа<nа);
-
st - строковая переменная для указания используемого алгоритма разложения (по умолчанию, st='svd');
-
meps - точность (по умолчанию, 1е-8).
Выходные переменные:
-
q0 - нуль-пространство матрицы А размера na*(na-rank(a)).
Используемые функции:
MATLAB: svd, qr, rank.
Пакет СНАУ: нет.
kroneck - вычисление характеристик структуры Кронекера
Синтаксис:
Nx = kroneck(a, b, meps)
Описание:
Функция Nx = kroneck(a, b, meps) вычисляет характеристики структуры Кронекера для прямоугольного пучка матриц.
Входные переменные:
-
a, b - компоненты прямоугольного пучка;
-
meps - точность оценки ранга.
Выходные переменные:
-
Nx = [Nl Nr N0 Ni] -параметры структуры Кронекера.
Используемые функции:
MATLAB: nargin, rank.
Пакет SNAE: нет.
numb - вычисление номера столбца матрицы
Синтаксис:
J = numb(jk, sk)
Описание:
Функция J = numb(jk, sk) вычисляет номер столбца матрицы, соответствующий элементу базиса с лексикографическим упорядочением (базис Кронекера)
![]()
Входные переменные:
-
jk - вектор [j1...jn] значений степени переменных x1...хn;
-
sk - вектор [s1...sn] максимальных значений степеней переменныx;
Выходные переменные:
-
J - номер столбца в матрице Ax.
Используемые функции: нет.
pencil - вычисление матриц пучка
Синтаксис:
[ax, bx, Nx] = pencil(q0, sx, meps)
Описание:
Функция [ax,bx,Nx]=pencil(q0,sx,meps) вычисляет матрицы пучка, если известно ядро q0x или q0y.
Входные переменные:
-
qo - ядро матрицы Ax исходной СНАУ;
-
sx - максимальная степень переменной x;
-
meps - точность вычисления ранга, по умолчанию 1e-8.
Выходные переменные:
-
ax, bx - прямоугольные матрицы пучка D(x) = ax - x*bx;
-
Nx - мультииндекс структуры Кронекера {Nl Nr N0 Ni}.
Используемые функции:
MATLAB: rank, size, norm.
Пакет СНАУ: нет.
permut - вычисление строки перестановок
Синтаксис:
P = permut(sx, sy, nv)
Описание:
Функция P = permut(sx, sy, nv) вычисляет cтроку перестановок элементов базиса при перемене местами переменных x и y.
Входные переменные:
-
sx - максимальная степень переменной x;
-
sy - максимальная степень переменной y;
-
nv - число элементов вектора свободных переменных v.
Выходные переменные:
-
P - строка перестановок элементов базиса.
Используемые функции:
MATLAB: нет.
Пакет СНАУ: numb.
poleq - вычисление компонентов матрицы вспомогательной СНАУ
Синтаксис:
Slx = poleq(a, b, t, n1, n2)
Описание:
Функция Slx = poleq(a, b, t, n1, n2) вычисляет составляющие матрицы для вспомогательной СНАУ вида
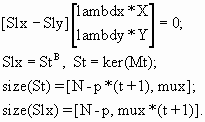
Входные переменные:
-
a, b - матрицы пучка D(x)=a-x*b;
-
t - степень полиномиального решения;
-
n1, n2 - диапазон столбцов, выделяемых из Slx.
Используемые функции
MATLAB: max, round, eval, size, zeros.
Пакет СНАУ: нет.
polsol - формирование вспомогательной СНАУ
Синтаксис:
[Dflx, Dfly, alrlx, alrly] = polsol(Dx, Dy, t, v)
Описание:
Функция [Dflx, Dfly, alrlx, alrly] = polsol(Dx, Dy, t, v) формирует вспомогательную систему нелинейных уравнений на этапе вычисления полиномиальных решений.
Входные переменные:
-
Dx, Dy - сингулярные пучки ax - x*bx, ay - y*by;
-
t, v - степени полиномиальных решений по переменным x и y.
Выходные переменные:
-
Dflx, Dfly - регулярные пучки вспомогательной СНАУ;
-
D0lx, D0ly - сингулярные пучки вспомогательной СНАУ.
Используемые функции:
MATLAB: length, rank, size.
Пакет СНАУ: ker, pencil, poleq, pr_table, struct.
pr_table - формирование таблицы RGSVD-разложения
Синтаксис:
pr_table(nk, mk, alr, ali)
Описание:
Функция pr_table(nk, mk, alr, ali) формирует на экране таблицу, связанную со структурой правых полиномиальных и бесконечных решений и являющуюся результатом RGSVD разложения пучка матриц:
k nk mk r0 r1 r2 r3 r4 r5 r6 J1 J2 J3 J4 J5 J6
1 2 2 0 0
2 2 2 0 0
3 2 1 1 0
4 1 1 0 0
5 1 1 0 0
6 1 1 0 0
7 1 0 1
Входные переменные:
-
nk - вектор dim.Ker(a);
-
mk - вектор dim.Im(b);
-
alr - мультииндекс правых полиномиальных решений;
-
ali - мультииндекс структур элементарных делителей для бесконечных собственных значений.
Используемые функции:
MATLAB: int2str.
Пакет СНАУ: нет.
pr_tablm - формирование таблицы характеристик матрицы Mt
Синтаксис:
pr_tablm(m, n, r, mu, alr)
Описание:
Функция pr_tablm(m, n, r, mu, alr) формирует на экране таблицу характеристик матрицы Mt следующего вида
s m n rnk mu alr
0 16 10 10 0 0
1 24 20 20 0 0
2 32 30 29 1 1
3 40 40 38 2 0
4 48 50 47 3 0
5 56 60 56 4 0
6 64 70 64 6 1
Входные переменные:
-
m - число строк матрицы Mt;
-
n - число столбцов матрицы Mt;
-
r - размерность образа dim.Im(Mt) (ранг матрицы Mt);
-
mu - размерность ядра dim.Ker(Mt);
-
alr - информационный вектор структуры Кронекера для пучка.
Используемые функции:
MATLAB: size.
Пакет СНАУ: wr3pos.
reduc - редукция числа переменных СНАУ
Синтаксис:
Ay = reduc(Axy, x, sx)
Описание:
Функция Ay = reduc(Axy, x, sx) осуществляет редукцию числа переменных СНАУ путем подстановки найденного решения x.
Входные переменные:
-
Axy - матрица СНАУ;
-
x - найденное решение;
-
sx - максимальная степень переменной x.
Выходные переменные:
-
Ay - редуцированная матрица СНАУ;
Используемые функции:
MATLAB: max, size.
Пакет СНАУ: нет.
rgsvd - вычисление RGSVD-разложения для пучка матриц
Синтаксис:
[a2, b2, n, m] = rgsvd(a1, b1, meps)
Описание:
Функция [a2, b2, n, m] = rgsvd(a1, b1, meps) вычисляет рекуррентное обобщенное сингулярное разложение для пары прямоугольных матриц.
Входные переменные:
-
a1, b1 - прямоугольные матрицы пучка D1(x) = a1 - x*b1;
-
meps - точность вычисления ранга (по умолчанию, 1e-8).
Выходные переменные:
-
a2, b2 - прямоугольные матрицы пучка D2(x) после одного шага RGSVD-разложения;
-
n - размерность dim.Ker(a);
-
m - размерность dim.Im(b).
Используемые функции:
MATLAB: rank, svd, size.
Пакет СНАУ: нет.
rmovcmpl - удаление из вектора комплексных элементов
Синтаксис:
w = rmovcmpl(v)
Описание:
Функция w = rmovcmpl(v) удаляет из вектора v комплекснозначные элементы.
Входные переменные:
-
v - вектор с реальными и комплексными элементами
Выходные переменные:
-
w - вектор без комплексных элементов
Используемые функции
MATLAB: find.
rmovel - удаление совпадающих элементов вектора
Синтаксис:
w = rmovel(v)
Описание:
Функция w = rmovel(v) удаляет из вектора v совпадающие элементы, формируя вектор w, не содержащий одинаковых элементов
Входные переменные:
-
v - исходный вектор.
Выходные переменные:
-
w - вектор, не содержащий одинаковых элементов.
Используемые функции:
MATLAB: length, find.
Пакет СНАУ: нет.
rmovstr - удаление совпадающих строк матрицы
Синтаксис:
w = rmovstr(v)
Описание:
Функция w = rmovstr(v) удаляет из матрицы V совпадающие строки, формируя матрицу W, не содержащую одинаковых строк.
Входные переменные:
-
v - исходная матрица.
Выходные переменные:
-
w - матрица, не содержащая одинаковых строк.
Используемые функции:
MATLAB: length, find.
Пакет СНАУ: нет.
solsnae1 - решение СНАУ от одной переменной
Синтаксис:
solsnae1
Описание:
Демонстрационный Script-файл, предназначенный для решения нелинейных алгебраических уравнений и систем таких уравнений от одной переменной.
% ********************************************************
%
% Решение
% систем нелинейных алгебраических уравнений (СНАУ)
% от одной переменной
% A*x = 0,
%
% ********************************************************
% A - матрица размера p*N;
% N - число столбцов матрицы A, равное длине вектора x;
% x - вектор алгебраической структуры
% sx jx
% [ x*..*x ... x*..*x ... 1 ],
%
% jx - степень переменной;
% sx - максимальная степень переменной.
%
solsnae2 - решение СНАУ от двух переменных
Синтаксис:
solsnae2
Описание:
Демонстрационный Script-файл, предназначенный для решения систем нелинейных алгебраических уравнений от двух переменных.
%
% ********************************************************
% Решение
% систем нелинейных алгебраических уравнений (СНАУ)
% от двух переменных:
%
% Axy*[x**y] = 0,
%
% ********************************************************
% Axy - матрица размера p*N;
% N - число столбцов матрицы Axy;
% x, y - вектора алгебраической структуры
% sx jx
% [ x*..*x ... x*..*x ... 1 ],
% sy jy
% [ y*..*y ... y*..*y ... 1 ]
% jx, jy - степени переменных;
% sx, sy - максимальные степени переменных;
% x**y - произведение Кронекера.
snae1 - решение СНАУ от одной переменной
Синтаксис:
[x, err] = snae1(Ax)
Описание:
Функция [x, err] = snae1(Ax) решает нелинейные алгебраические уравнения и системы таких уравнений от одной переменной.
Входные переменные:
-
Ax - матрица коэффициентов СНАУ.
Выходные переменные:
-
x - решения СНАУ от одной переменной;
-
err - символьная переменная, принимающая значение 'none_solution', что означает отсутствие решения.
Используемые функции:
MATLAB: null, size, length, eig, sort.
Пакет СНАУ: pencil, struct.
snae2 - решение СНАУ от двух переменных
Синтаксис:
[x, y, err] = snae2(Axy, sx, sy)
Описание:
Функция [x, y, err] = snae2(Axy, sx, sy) решает системы нелинейных алгебраических уравнений от двух переменных x и у.
Входные переменные:
-
Axy - матрица коэффициентов СНАУ;
-
sx - максимальная степень переменной x;
-
sy - максимальная степень переменной y.
Выходные переменные:
-
{x, y} - решения СНАУ;
-
err - строковая переменная, которая может принимать одно из двух значений:
- 'Infinity' - количество решений бесконечно;
- 'None_solution' - СНАУ не имеет решений или приводима.
Используемые функции:
MATLAB: null.
ППП СНАУ: pencil, solssp, reduc, rmovstr, snae1.
solssp, dsolssp - решение системы спектральных задач
Синтаксис:
[x, y, class] = solssp(ax, bx, ay, by)
[x, y, class] = dsolssp(ax, bx, ay, by)
Описание:
Функция [x, y, class] = solssp(ax, bx, ay, by) решает следующую систему спектральных задач:
(ax - x*bx)*Rx = 0;
(ay - y*by)*Ry = 0;
[Rx -Ry][X Y]'= 0.
где
ax, bx, ay, ay - матрицы сингулярных пучков D(x), D(y), порожденные ker(A);
Rx, Ry - матрицы собственных векторов спектральных задач по переменным x, y;
X, Y - матрицы размера sy-(p-1)*d и sx-(p-d)*d;
d - дефект матрицы [Rx -Ry].
Функция [x, y, class] = dsolssp(ax, bx, ay, by) выполняет те же операции и предназначена для демонстрационной версии.
Входные переменные:
-
ax, bx, ay, by - сингулярные пучки матриц.
Выходные переменные:
-
[x y] - возможные пары решений СНАУ;
-
class - информационный вектор, указывающий принадлежность решения к одному из 4-х классов
Используемые функции:
MATLAB: нет.
Пакет СНАУ: struct, pr_table, dimm, poleq.
ssnae2, dsnae2 - решение СНАУ от двух переменных
Синтаксис:
[x, y, err] = ssnae2(Axy, P, sx, sy, nv)
[x, y, err] = dsnae2(Axy, P, sx, sy, nv)
Описание:
Функция [x, y, err] = ssnae2(Axy, P, sx, sy, nv) решает системы нелинейных алгебраических уравнений от двух переменных x и у.
Функция [x, y, err] = dsnae2(Axy, P, sx, sy, nv) выполняет те же операции и предназначена для демонстрационной версии.
Входные переменные:
-
Axy - матрица коэффициентов СНАУ;
-
Р - матрица перестановок;
-
sx - максимальная степень переменной x;
-
sy - максимальная степень переменной y;
-
nv - длина вектора свободных переменных.
Выходные переменные:
-
{x,y} - пары решений СНАУ;
-
err - символьная переменная, принимающая значения:
- infinity - СНАУ имеет бесчисленное множество решений или приводима;
- none_solution - СНАУ не имеет решений.
Используемые функции:
MATLAB: null.
Пакет СНАУ: pencil, solssp, reduc, snae1.
struct - вычисляет структуру Кронекера прямоугольного пучка
Синтаксис:
[alr, af, bf, nk, mk, ali] = struct(a, b)
Описание:
Функция [alr, af, bf, nk, mk, ali] = struct(a, b) вычисляет структуру Кронекера прямоугольного пучка матриц.
Входные переменные:
-
a, b - прямоугольные матрицы пучка D(x) = a - x*b.
Выходные переменные:
-
alr - мультииндекс правых полиномиальных решений;
-
af, bf - регулярная часть ядра D(x);
-
nk - вектор dim.Ker(a);
-
mk - вектор dim.Im(b) ;
-
ali - мультииндекс числа структур элементарных делителей для бесконечных собственных значений.
Используемые функции:
MATLAB: rgsvd, size, norm.
Пакет СНАУ: нет.
trunc - обработка и усечение вектора решений
Синтаксис:
tx = trunc(x)
Описание:
Функция tx = trunc(x) обрабатывает вектор x, округляя значения до действительных или чисто мнимых, удаляя элементы типа NAN и присваивая элементам, превосходящим 1012, значения inf.
Входные переменные:
-
x - вектор возможных решений СНАУ.
Выходные переменные:
-
tx - преобразованный вектор.
Используемые функции: нет.
wr3pos - подсчет количества цифр в числе
Синтаксис:
CHAR3 = wr3pos(id)
Описание:
Функция CHAR3 = wr3pos(id) формирует строку, содержащую информацию о количестве цифр в выводимом числе.
Используемые функции:
MATLAB: int2str.
Пакет СНАУ: нет.
Комментарии