Восстановление искаженных изображений является одной из наиболее интересных и важных проблем в задачах обработки изображений – как с теоретической, так и с практической точек зрения. Частными случаями являются размытие из-за неправильного фокуса и смаз – эти дефекты, с которым каждый из вас хорошо знаком, очень сложны в исправлении – именно они и выбраны темой статьи. С остальными искажениями (шум, неправильная экспозиция, дисторсия) человечество научилось эффективно бороться, соответствующие инструменты есть в каждом уважающем себя фоторедакторе. 

Почему же для устранения смаза и расфокусировки практически ничего нету (unsharp mask не в счет) – может быть это в принципе невозможно? На самом деле возможно – соответствующий математический аппарат начал разрабатываться примерно 70 лет назад, но, как и для многих других алгоритмов обработки изображений, все это нашло широкое применение только в недавнее время. Вот, в качестве демонстрации вау-эффекта, пара картинок:

Я не стал использовать замученную Лену, а нашел свою фотку Венеции. Правое изображение честно получено из левого, причем без использования ухищрений типа 48-битного формата (в этом случае будет 100% восстановление исходного изображения) – слева самый обычный PNG, размытый искусственно. Результат впечатляет… но на практике не все так просто. Под катом подробный обзор теории и практические результаты. 
Осторожно, много картинок в формате PNG!

Введение

Начнем издалека. Многие считают, что размытие необратимая операция и информация безвозвратно теряется, т.к. каждый пиксель превращается в пятно, все смешивается, а при большом радиусе размытия так и вовсе получим однородный цвет по всему изображению. Это не совсем так – вся информация просто перераспределяется по некоторому закону и может быть однозначно восстановлена с некоторыми оговорками. Исключение составляет лишь края изображения шириной в радиус размытия – там полноценное восстановление невозможно.

Продемонстрируем это «на пальцах», используя небольшой пример для одномерного случая – представим что у нас есть ряд из пикселей со значениями:
x1 | x2 | x3 | x4… – Исходное изображение

После искажения значение каждого пикселя суммируется со значением левого, т.е. x’i = xi + xi-1. По идее, надо еще поделить на 2, но опустим это для простоты. В результате имеем размытое изображения со значениями пикселей:
x1 + x0 | x2 + x1 | x3 + x2 | x4 + x3… – Размытое изображение

Теперь будем пробовать восстанавливать, вычтем последовательно по цепочке значения по схеме – из второго пиксела первый, из третьего результат второго, из четвертого результат третьего и так далее, получим:
x1 + x0 | x2 — x0 | x3 + x0 | x4 — x0… – Восстановленное изображение

В итоге вместо размытого изображения получили исходное изображение, к пикселям которого добавлена неизвестная константа x0 с чередующимся знаком. Это уже намного лучше – эту константу можно подобрать визуально, можно предположить, что она примерно равна значению x1, можно автоматически подобрать с таким критерием, чтобы значения соседних пикселей «скакали» как можно меньше и т.д. Но все меняется, как только мы добавляем шум (которые всегда есть в реальных изображениях). При описанной схеме на каждом шаге будет накапливаться вклад шума в общую составляющую, что в итоге может дать совершенно неприемлемый результат, но, как мы убедились, восстановление вполне реально даже таким примитивным способом.

Модель процесса искажения

А теперь перейдем к более формальному и научному описанию этих процессов искажения и восстановления. Будем рассматривать только полутоновые черно-белые изображения в предположении, что для обработки полноцветного изображения достаточно повторить все необходимые шаги для каждого из цветовых каналов RGB. Введем следующие обозначения:
f(x, y) – исходное неискаженное изображение
h(x, y) – искажающая функция
n(x, y) – аддитивный шум
g(x, y) – результат искажения, т.е. то, что мы наблюдаем в результате (смазанное или расфокусированное изображение)

Сформулируем модель процесса искажения следующим образом:
g(x, y) = h(x, y) * f(x, y) + n(x, y) (1)

Задача восстановления искаженного изображения заключается в нахождении наилучшего приближения f'(x, y) исходного изображения. Рассмотрим каждую составляющую более подробно. С f(x, y) и g(x, y) все достаточно понятно. А вот про функцию h(x, y) нужно сказать пару слов – что же она из себя представляет? В процессе искажения каждый пиксель исходного изображения превращается в пятно для случая расфокусировки и в отрезок для случая простого смаза. Либо же можно сказать наоборот, что каждый пиксель искаженного изображения «собирается» из пикселей некоторой окрестности исходного изображения. Все это друг на друга накладывается и в результате мы получаем искаженное изображение. То, по какому закону размазывается или собирается один пиксель и называется функцией искажения. Другие синонимы – PSF (Point spread function, т.е. функция распределения точки), ядро искажающего оператора, kernel и другие. Размерность этой функции, как правило меньше размерности самого изображения – к примеру, в начальном рассмотрении примера «на пальцах» размерность функции была 2, т.к. каждый пиксель складывался из двух. 

Искажающие функции

Посмотрим как выглядят типичные искажающие функции. Здесь и далее будем использовать ставший уже стандартным для таких целей инструмент – Matlab, он содержит в себе все необходимое для самых разнообразных экспериментов с обработкой изображений (и не только) и позволяет сосредоточиться на самих алгоритмах, перекладывая всю рутинную работу на библиотеки функций. Впрочем, за это приходится расплачиваться производительностью. Итак, вернемся к PSF, вот примеры их вида:

PSF в случае размытия по Гауссу функцией fspecial('gaussian', 30, 8);

PSF в случае смаза фунцией fspecial('motion', 40, 45);

Операция применения искажающей функции к другой функции (к изображению, в данном случае) называется сверткой (convolution), т.е. некоторая область исходного изображения сворачивается в один пиксель искаженного изображения. Обозначается через оператор «*», не путать с обычным умножением! Математически для изображения f с размерами M x N и искажающей функции h c размерами m x n это записывается так: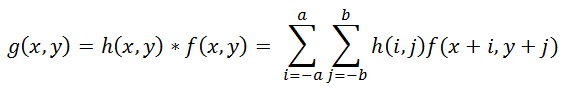 

 (2)

Где a = (m — 1) / 2, b = (n – 1) / 2. Операция, обратная свертке, называется деконволюцией (deconvolution) и решение такой задачи весьма нетривиально.

Модель шума

Осталось рассмотреть последнее слагаемое, отвечающее за шум, n(x, y) в формуле (1). Причины шума в цифровых сенсорах могут быть самыми разными, но основные это – тепловые колебания и темновые токи. На величину шума также влияет ряд факторов, таких как значение ISO, тип матрицы, размер пикселя, температура, электромагнитные наводки и пр. В большинстве случаев шум является Гауссовым (который задается двумя параметрами – средним и дисперсией), а также является аддитивным, не коррелирует с изображением и не зависит координат пикселя. Последние три предположения являются очень важными для дальнейшей работы.

Теорема о свертке

Вернемся теперь к первоначальной постановке задачи восстановления – нам необходимо каким-то образом обратить свертку, при этом не забывая про шум. Из формулы (2) видно, что получить f(x, y) из g(x, y) не так-то просто – если решать, что называется, «в лоб», то получится огромная система уравнений. Но на помощь к нам приходит преобразование Фурье, не будем подробно на нем останавливаться, по этой теме уже было сказано немало. Так вот, есть такая теорема о свертке, которая гласит, что операция свертки в пространственной области эквивалентна обычному умножению в частотной области (причем умножение поэлементное, а не матричное). Соответственно, операция обратная свертке эквивалентна делению в частотной области, т.е это можно записать как: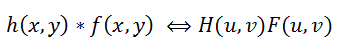
 (3)

Где H(u, v), F(u, v) – Фурье-образы соответствующих функций. Значит процесс искажения из формулы (1) можно переписать в частотной области как: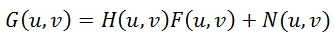
 (4)

Инверсная фильтрация

Тут же напрашивается поделить это равенство на H(u, v) и получить следующую оценку F^(u, v)исходного изображения: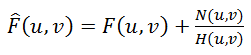
 (5)
Это называется инверсной фильтрацией, но на практике практически никогда не работает. Почему же? Чтобы ответить на этот вопрос посмотрим на последнее слагаемое в формуле (5) – если функция H(u, v) принимает значение близкие к нулю или нулевые, то вклад этого слагаемого будет доминирующим. Это практически всегда встречается в реальных примерах – для объяснения этого вспомним как выглядит спектр после преобразование Фурье. 
 
Берем исходное изображение, 

преобразуем его в полутоновое и, используя Matlab, получаем спектр:

% Load image
I = imread('image_src.png');
figure(1); imshow(I); title('Исходное изображение'); 
% Convert image into grayscale
I = rgb2gray(I);
% Compute Fourier Transform and center it
fftRes = fftshift(fft2(I));
% Show result
figure(2); imshow(mat2gray(log(1+abs(fftRes)))); title('FFT - Амплитудный спектр (логарифмическая шкала)');
figure(3); imshow(mat2gray(angle(fftRes))); title('FFT - Фазовый спектр');

В результате получаем две компоненты: амплитудный и фазовый спектры. Про фазу, кстати, многие забывают. Обратите внимание, что амплитудный спектр показан в логарифмической шкале, т.к. его значения варьируются очень сильно – на несколько порядков, в центре максимальные значения (порядка миллионов) и быстро убывают практически до нулевых по мере удаления от центра. Именно из-за этого инверсная фильтрация будет работать только при нулевых или практически нулевых значениях шума. Продемонстрируем это на практике с помощью следующего скрипта:

% Load image
I = im2double(imread('image_src.png')); 
figure(1); imshow(I); title('Исходное изображение');
% Blur image
Blurred = imfilter(I, PSF,'circular','conv' );
figure(2); imshow(Blurred); title('Размытое изображение');
% Add noise
noise_mean = 0;
noise_var = 0.0;
Blurred = imnoise(Blurred, 'gaussian', noise_mean, noise_var);
% Deconvolution
figure(3); imshow(deconvwnr(Blurred, PSF, 0)); title('Результат');

noise_var = 0.0000001                            noise_var = 0.000005

Хорошо видно, что добавление даже очень небольшого шума приводит к значительным 
помехам, что сильно ограничивает практическое применение метода.

Существующие подходы для деконволюции

Но есть подходы, которые учитывают учитывают наличие шума на изображении – один из самых известных и самых первых, это фильтр Винера (Wiener). Он рассматривает изображение и шум как случайные процессы и находит такую оценку f' для неискаженного изображения f, чтобы среднеквадратическое отклонение этих величин было минимальным. Минимум этого отклонения достигается на функции в частотной области:
 (6)
Этот результат был получине Винером в 1942 году. Функцией S здесь обозначаются энергетические спектры шума и исходного изображения соответственно – поскольку, эти величины редко бывают известны, то дробь Sn / Sf заменяют на некоторую константу K, которую можно приблизительно охарактеризовать как соотношение сигнал-шум.

Следующий метод, это «сглаживающая фильтрация методом наименьших квадратов со связью», другие названия: «фильтрация по Тихонову», «Тихоновская регуляризация». Его идея заключается в формулировке задачи в матричном виде с дальнейшем решением соответствующей задачи оптимизации. Это решение записывается в виде:
 (7)
Где y – параметр регуляризации, а P(u, v) – Фурье-преобразование оператора Лапласа (матрицы 3 * 3).

Еще один интересный подход предложили независимо Ричардосн [Richardson, 1972] и Люси [Lucy, 1974]. Метод так и называется «метод Люси-Ричардсона». Его отличительная особенность в том, что он является нелинейным, в отличие от первых трех – что потенциально может дать лучший результат. Вторая особенность – метод является итерационным, соответственно возникают трудности с критерием останова итераций. Основная идея состоит в использовании метода максимального правдоподобия для которого предполагается, что изображение подчиняется распределению Пуассона. Формулы для вычисления достаточно простые, без использования преобразования Фурье – все делается в пространственной области:
 (8)
Здесь символом «*», как и раньше, обозначается операция свертки. Этот метод широко используется в программах для обработки астрономических фотографий – в них использование деконволюции (вместо unsharp mask, как в фоторедакторах) является стандартом де-факто. Вычислительная сложность метода очень большая – обработка средней фотографии, в зависимости от количества итераций, может знанимать многие часы и даже дни.

Последний рассматриваемый метод, а вернее, целое семейство методов, которые сейчас активно разрабатываются и развиваются- это слепая деконволюция (blind deconvolution). Во всех предыдущих методах предполагаслось, что искажающая функция PSF точно известна, в реальности это не так, обычно PSF известна лишь приблизительно по характеру видимых искажений. Слепая деконволюция как раз является попыткой учитывать это. Принцип достаточно простой, если не кглубляться в детали - выбирается первое приближение PSF, далее по одному из методов делается деконволюция, после чего некоторым критерием определяется степень качества, на основе нее уточняется функция PSF и итерация повторяется до достижения нужного резуль

Практика

Теперь с теорией все – перейдем к практике, начнем со сравнения перечисленных методов на изображении с искусственным размытием и шумом.

% Load image
I = im2double(imread('image_src.png'));
figure(1); imshow(I); title('Исходное изображение');

% Blur image
PSF = fspecial('disk', 15);
Blurred = imfilter(I, PSF,'circular','conv' );

% Add noise
noise_mean = 0;
noise_var = 0.00001;
Blurred = imnoise(Blurred, 'gaussian', noise_mean, noise_var);
figure(2); imshow(Blurred); title('Размытое изображение');
estimated_nsr = noise_var / var(Blurred(:));

% Restore image
figure(3), imshow(deconvwnr(Blurred, PSF, estimated_nsr)), title('Wiener');
figure(4); imshow(deconvreg(Blurred, PSF)); title('Regul');
figure(5); imshow(deconvblind(Blurred, PSF, 100)); title('Blind');
figure(6); imshow(deconvlucy(Blurred, PSF, 100)); title('Lucy');

Результаты:


Фильтр Винера


Регуляризация по Тихонову


Фильтр Люси-Ричардсона


Слепая деконволюция

Заключение

И в конце первой части немного затронем примеры реальных изображений. До этого все искажения были искусственными, что конечно хорошо для обкатки и изучения, но очень интересно посмотреть, как все это будет работать с настоящими фотографиями. Вот один пример такого изображения, снятого зеркалкой Canon 500D с ручным уводом фокуса:

Далее запускаем несложный скрипт:

% Load image
I = im2double(imread('IMG_REAL.PNG'));
figure(1); imshow(I); title('Исходное изображение');

%PSF
PSF = fspecial('disk', 8);
noise_mean = 0;
noise_var = 0.0001;
estimated_nsr = noise_var / var(I(:));

I = edgetaper(I, PSF);
figure(2); imshow(deconvwnr(I, PSF, estimated_nsr)); title('Результат');

И получаем следующий результат: 

Как видно, на изображении появились новые детали, четкость стала гораздо выше, правда появились и помехи в виде "звона" на контрастных границах.

И пример с реальным смазом — для его осуществления фотоаппарат был установлен на штатив, выставлена относительно длинная выдержка и равномерным движением в момент срабатывания затвора был получен смаз:

Скрипт примерно тот же, только тип PSF теперь "motion":

% Load image
I = im2double(imread('IMG_REAL_motion_blur.PNG'));
figure(1); imshow(I); title('Исходное изображение');

%PSF
PSF = fspecial('motion', 14, 0);
noise_mean = 0;
noise_var = 0.0001;
estimated_nsr = noise_var / var(I(:));

I = edgetaper(I, PSF);
figure(2); imshow(deconvwnr(I, PSF, estimated_nsr)); title('Результат');

Результат: 

Качество, опять же, заметно улучшилось - стали различимы рамы на окнах, машины.

Артефакты уже другие, нежели в предыдущем примере с расфокусировкой.

Литература

Гонсалес Р., Вудс Р. Цифровая обработка изображений
Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB